| Citation: |
Qiang Cao, Shishen Yan. The predicaments and expectations in development of magnetic semiconductors[J]. Journal of Semiconductors, 2019, 40(8): 081501. doi: 10.1088/1674-4926/40/8/081501
****
Q Cao, S S Yan, The predicaments and expectations in development of magnetic semiconductors[J]. J. Semicond., 2019, 40(8): 081501. doi: 10.1088/1674-4926/40/8/081501.
|
The predicaments and expectations in development of magnetic semiconductors
DOI: 10.1088/1674-4926/40/8/081501
More Information
-
Abstract
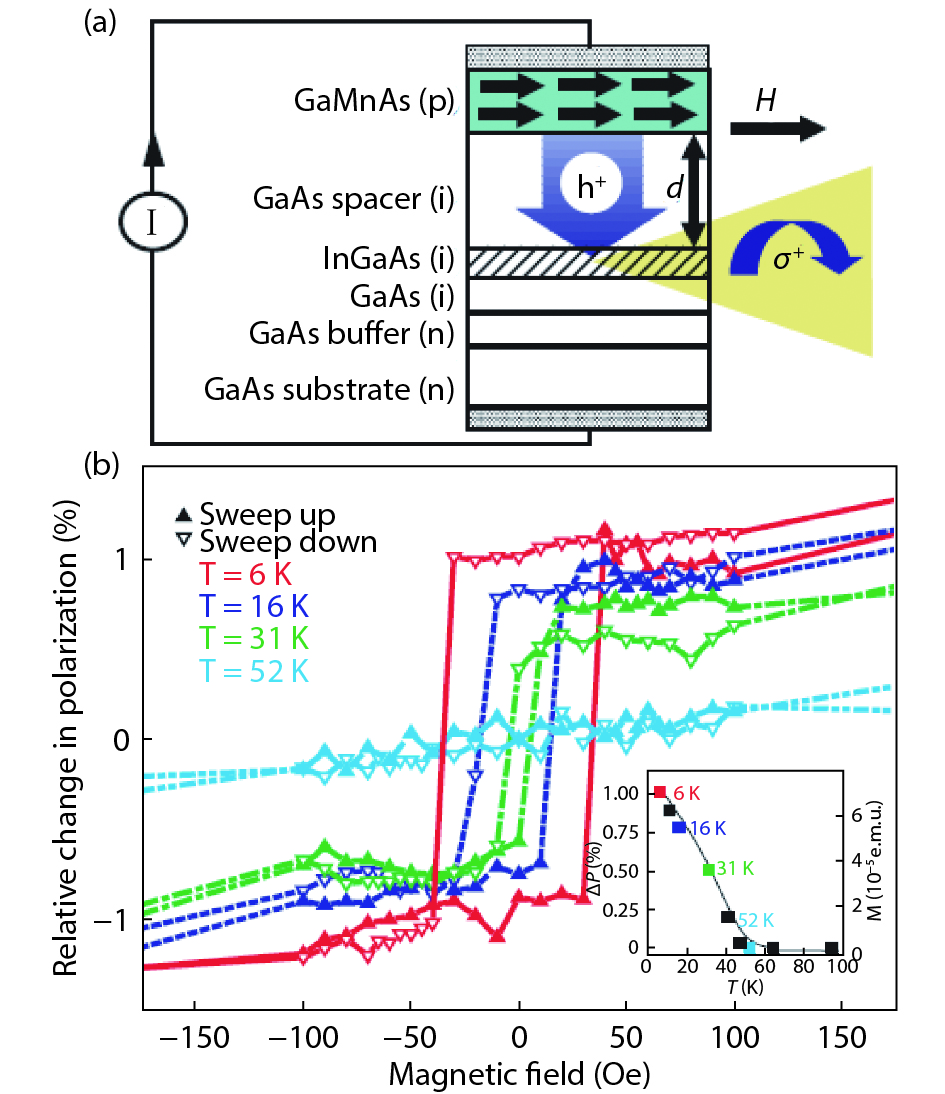
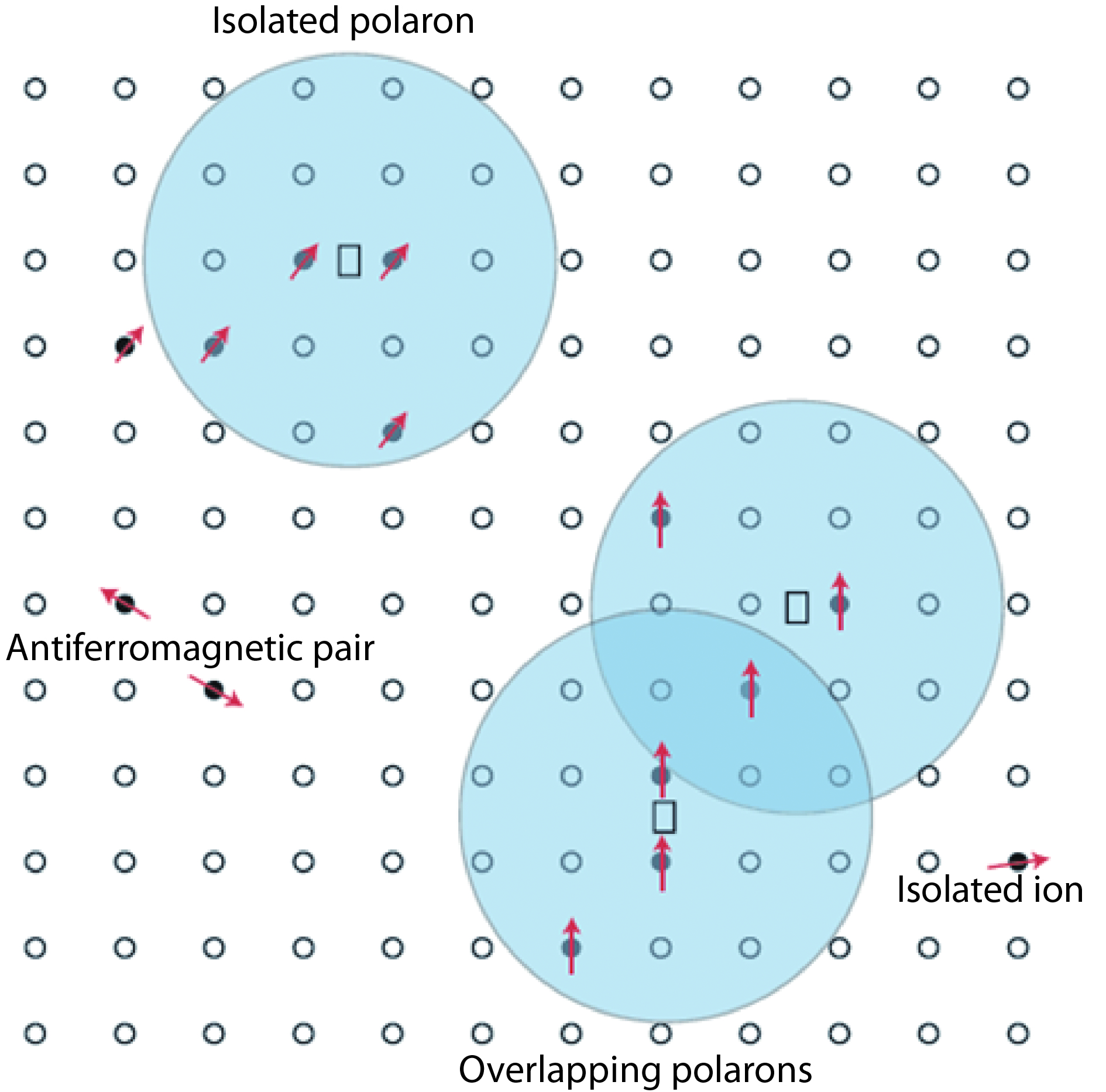
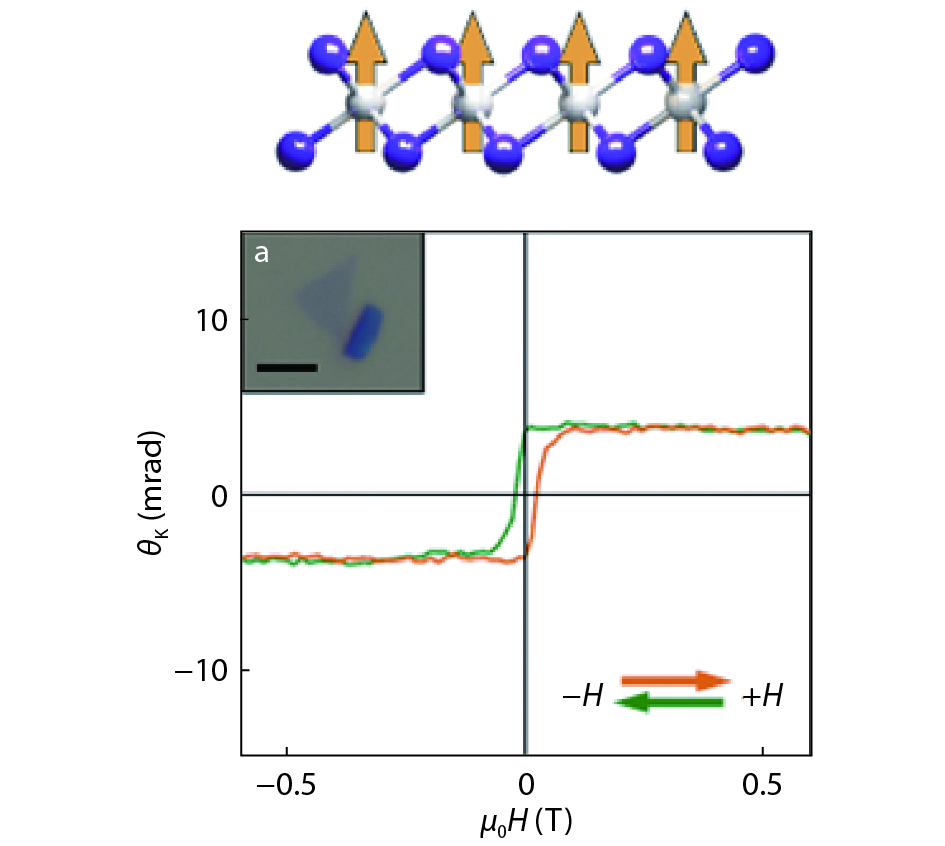
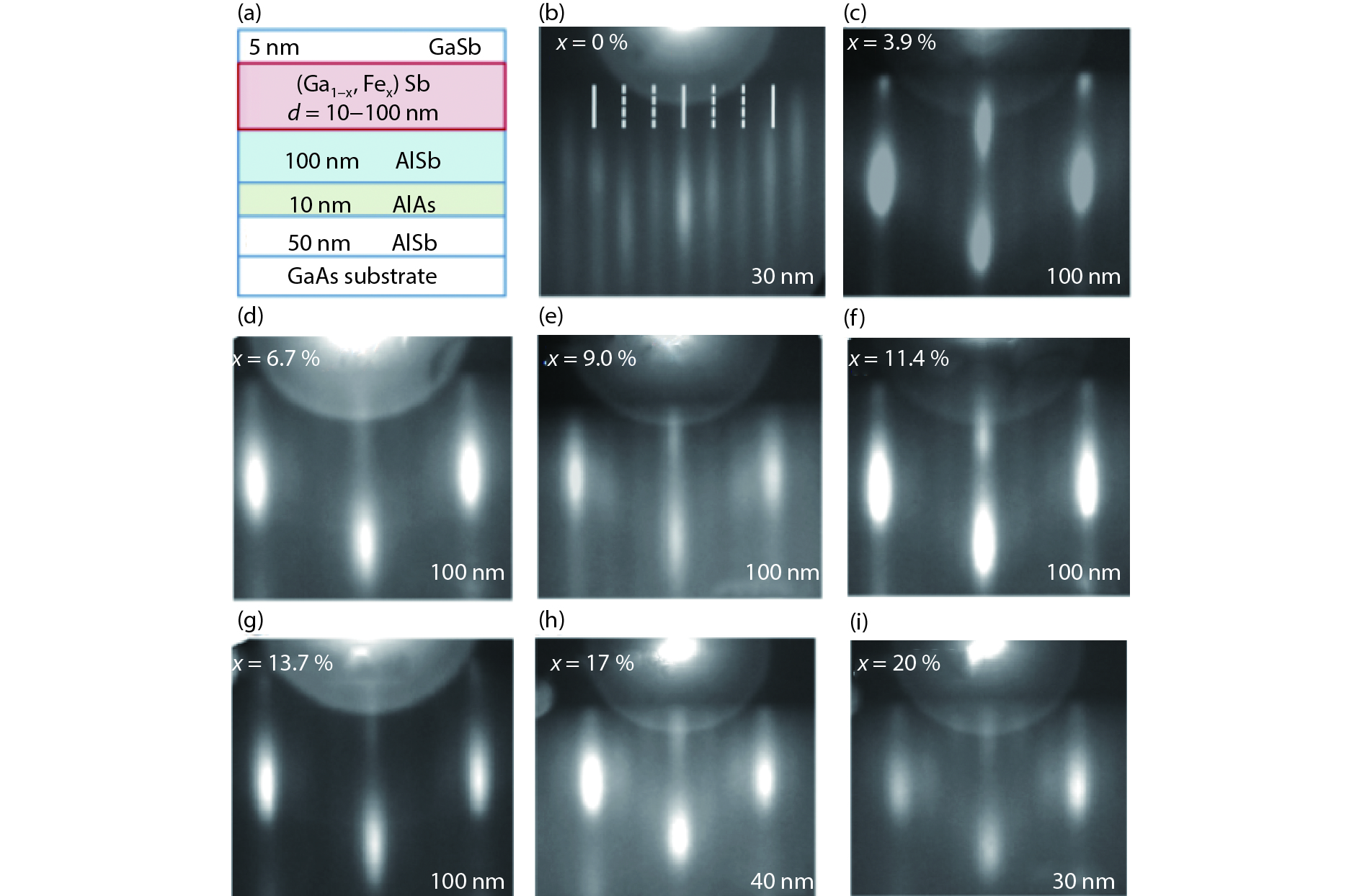
Over the past half a century, considerable research activities have been directing towards the development of magnetic semiconductors that can work at room temperature. These efforts were aimed at seeking room temperature magnetic semiconductors with strong and controllable s, p-d exchange interaction. With this s, p-d exchange interaction, one can utilize the spin degree of freedom to design applicable spintronics devices with very attractive functions that are not available in conventional semiconductors. Here, we first review the progress in understanding of this particular material and the dilemma to prepare a room temperature magnetic semiconductor. Then we discuss recent experimental progresses to pursue strong s, p-d interaction to realize room temperature magnetic semiconductors, which are achieved by introducing a very high concentration of magnetic atoms by means of low-temperature nonequilibrium growth. -
References
[1] Wolf S A, Awschalom D D, Buhrman R A, et al. Spintronics: a spin-based electronics vision for the future. Science, 2001, 294, 1488 doi: 10.1126/science.1065389[2] Ando K. Seeking Room-temperature ferromagnetic semiconductors. Science, 2006, 312, 1883 doi: 10.1126/science.1125461[3] Fabian A M A J, Ertler C, Stano P, et al. Semiconductor spintronics. Acta Physica Slovaca, 2007, 57, 565[4] Jungwirth T. Spin-dependent phenomena and device concepts explored in (Ga,Mn)As. Rev Mod Phys, 2014, 86, 855 doi: 10.1103/RevModPhys.86.855[5] Dietl T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat Mater, 2010, 9, 965 doi: 10.1038/nmat2898[6] Chambers S. Is it really intrinsic ferromagnetism. Nat Mater, 2010, 9, 956 doi: 10.1038/nmat2905[7] Seife C. Can the laws of physics be unified. Science, 2005, 309, 82 doi: 10.1126/science.309.5731.82[8] Chambers S, Droubay T, Wang C, et al. Ferromagnetism in oxide semiconductors. Mater Today, 2006, 9, 28 doi: 10.1016/S1369-7021(06)71692-3[9] Mauger A, Godart C. The magnetic, optical, and transport properties of representatives of a class of magnetic semiconductors: The europium chalcogenides. Phys Rep, 1986, 141, 51 doi: 10.1016/0370-1573(86)90139-0[10] Furdyna J K. Diluted magnetic semiconductors. J Appl Phys, 1988, 64, R29 doi: 10.1063/1.341700[11] Ohno H. Making nonmagnetic semiconductors ferromagnetic. Science, 1998, 281, 951 doi: 10.1126/science.281.5379.951[12] Matthias B T, Bozorth R M, Vleck J H Van. Ferromagnetic interaction in EuO. Phys Rev Lett, 1961, 7, 160 doi: 10.1103/PhysRevLett.7.160[13] Zhao L, Zhang B, Pang Q, et al. Chemical synthesis and magnetic properties of dilute magnetic ZnTe: Cr crystals. Appl Phys Lett, 2006, 89, 092111 doi: 10.1063/1.2337561[14] Pekarek T M, Miotkowski I, Crooker B C. Magnetic measurements on Cd1– xCr xTe and Zn1– xCr xTe. J Appl Phys, 1996, 79, 6436 doi: 10.1063/1.361963[15] Jain M K. Diluted magnetic semiconductors. Singapore: World Scientific Publishing Co. Ltd., 1991[16] Turner A E, Gunshor R L, Datta S. New class of materials for optical isolators. Appl Opt, 1983, 22, 3152 doi: 10.1364/AO.22.003152[17] Ohno H, Shen A, Matsukura F, et al. (Ga,Mn)As: A new diluted magnetic semiconductor based on GaAs. Appl Phys Lett, 1996, 69, 363 doi: 10.1063/1.118061[18] Wang H, Chen L, Zhao J. Enhancement of the Curie temperature of ferromagnetic semiconductor (Ga,Mn)As. Sci Chin Phys, Mechan Astron, 2013, 56, 99 doi: 10.1007/s11433-012-4959-3[19] Ohno H, Chiba D, Matsukura F, et al. Electric-field control of ferromagnetism. Nature, 2000, 408, 944 doi: 10.1038/35050040[20] Ohno Y, Young D K, Beschoten B, et al. Electrical spin injection in a ferromagnetic semiconductor heterostructure. Nature, 1999, 402, 790 doi: 10.1038/45509[21] Jeudy V, Curiale J, Adam J P, et al. Current induced domain wall motion in GaMnAs close to the Curie temperature. J Phys: Conden Matter, 2011, 23, 446004 doi: 10.1088/0953-8984/23/44/446004[22] Yamanouchi M, Chiba D, Matsukura F, et al. Current-assisted domain wall motion in ferromagnetic semiconductors. Jpn J Appl Phys, 2006, 45, 3854 doi: 10.1143/JJAP.45.3854[23] Chernyshov A, Overby M, Liu X, et al. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin-orbit magnetic field. Nat Phys, 2009, 5, 656 doi: 10.1038/nphys1362[24] Jaworski C M, Yang J, Mack S, et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor. Nat Mater, 2010, 9, 898 doi: 10.1038/nmat2860[25] Jaworski C M, Yang J, Mack S, et al. Spin-Seebeck effect: a phonon driven spin distribution. Phys Rev Lett, 2011, 106 doi: 10.1103/PhysRevLett.106.186601[26] Tang H X, Kawakami R K, Awschalom D D, et al. Giant planar Hall effect in epitaxial (Ga,Mn)As devices. Phys Rev Lett, 2003, 90, 107201 doi: 10.1103/PhysRevLett.90.107201[27] Gould C, Rüster C, Jungwirth T, et al. Tunneling anisotropic magnetoresistance: a spin-valve-like tunnel magnetoresistance using a single magnetic layer. Phys Rev Lett, 2004, 93, 117203 doi: 10.1103/PhysRevLett.93.117203[28] Olejník K, Owen M H S, Novák V., et al Enhanced annealing, high Curie temperature, and low-voltage gating in (Ga,Mn)As: A surface oxide control study. Phys Rev B, 2008, 78, 054403 doi: 10.1103/PhysRevB.78.054403[29] Chen L, Yang X, Yang F, et al. Enhancing the Curie temperature of ferromagnetic semiconductor (Ga,Mn)As to 200 K via nanostructure engineering. Nano Lett, 2011, 11, 2584 doi: 10.1021/nl201187m[30] Dietl T, Ohno H, Matsukura F, et al. Zener Model description of ferromagnetism in zinc-blende magnetic semiconductors. Science, 2000, 287, 1019 doi: 10.1126/science.287.5455.1019[31] Hong N H, Sakai J, Hassini A. Magnetic properties of V-doped ZnO thin films. J Appl Phys, 2005, 97, 10D312 doi: 10.1063/1.1848451[32] Ramachandran S, Tiwari A, Narayan J, et al. Epitaxial growth and properties of Zn1– xV xO diluted magnetic semiconductor thin films. Appl Phys Lett, 2005, 87, 172502 doi: 10.1063/1.2112185[33] Saeki H, Tabata H, Kawai T. Magnetic and electric properties of vanadium doped ZnO films. Solid State Commun, 2001, 120, 439 doi: 10.1016/S0038-1098(01)00400-8[34] Venkatesan M, Fitzgerald C B, Lunney J G, et al. Anisotropic ferromagnetism in substituted zinc oxide. Phys Rev Lett, 2004, 93, 177206 doi: 10.1103/PhysRevLett.93.177206[35] Hong N H, Sakai J, Huong N T, et al. Role of defects in tuning ferromagnetism in diluted magnetic oxide thin films. Phys Rev B, 2005, 72, 045336 doi: 10.1103/PhysRevB.72.045336[36] Fan J P, Quan Z Y, Xu X H. Tunable magnetic and transport properties of p-type ZnMnO films with n-type Ga, Cr, and Fe codopants. Appl Phys Lett, 2013, 102, 102407 doi: 10.1063/1.4795519[37] Kundaliya D C, Ogale S B, Lofland S E, et al. On the origin of high-temperature ferromagnetism in the low-temperature-processed Mn–Zn–O system. Nat Mater, 2004, 3, 709 doi: 10.1038/nmat1221[38] Cheng X M, Chien C L. Magnetic properties of epitaxial Mn-doped ZnO thin films. J Appl Phys, 2003, 93, 7876 doi: 10.1063/1.1556125[39] Sharma P, Gupta A, Rao K V, et al. Ferromagnetism above room temperature in bulk and transparent thin films of Mn-doped ZnO. Nat Mater, 2003, 2, 673 doi: 10.1038/nmat984[40] Norton D P, Pearton S J, Hebard A F, et al. Ferromagnetism in Mn-implanted ZnO: Sn single crystals. Appl Phys Lett, 2003, 82, 239 doi: 10.1063/1.1537457[41] Park S Y, Kim P J, Lee Y P, et al. Realization of room-temperature ferromagnetism and of improved carrier mobility in Mn-doped ZnO film by oxygen deficiency, introduced by hydrogen and heat treatments. Adv Mater, 2007, 19, 3496 doi: 10.1002/(ISSN)1521-4095[42] Cao Q, Fu M, Liu G, et al. Local vibrational modes competitions in Mn-doped ZnO epitaxial films with tunable ferromagnetism. J Appl Phys, 2014, 115, 243906 doi: 10.1063/1.4885735[43] Wei X X, Song C, Geng K W, et al. Local Fe structure and ferromagnetism in Fe-doped ZnO films. J Phys: Conden Matter, 2006, 18, 7471 doi: 10.1088/0953-8984/18/31/037[44] Liu G L, Cao Q, Deng J X, et al. High Tc ferromagnetism of Zn1– xCo xO diluted magnetic semiconductors grown by oxygen plasma-assisted molecular beam epitaxy. Appl Phys Lett, 2007, 90, 052504 doi: 10.1063/1.2437111[45] Cao Q, Deng J X, Liu G L, et al. Epitaxial properties of Co-doped ZnO thin films grown by plasma assisted molecular beam epitaxy. Chin Phys Lett, 2007, 24, 2951 doi: 10.1088/0256-307X/24/10/066[46] Cao Q, He S, Deng Y, et al. Raman scattering investigations on Co-doped ZnO epitaxial films: Local vibration modes and defect associated ferromagnetism. Curr Appl Phys, 2014, 14, 744 doi: 10.1016/j.cap.2014.03.011[47] Chen Z Y, Chen Z Q, Zou B, et al. Defect mediated ferromagnetism in Ni-doped ZnO nanocrystals evidenced by positron annihilation spectroscopy. J Appl Phys, 2012, 112, 083905 doi: 10.1063/1.4759136[48] Wakano T, Fujimura N, Morinaga Y, et al. Magnetic and magneto-transport properties of ZnO: Ni films. Physica E, 2001, 10, 260 doi: 10.1016/S1386-9477(01)00095-9[49] Buchholz D B, Chang R P H, Song J Y, et al. Room-temperature ferromagnetism in Cu-doped ZnO thin films. Appl Phys Lett, 2005, 87, 082504 doi: 10.1063/1.2032588[50] Sudakar C, Thakur J S, Lawes G, et al. Ferromagnetism induced by planar nanoscale CuO inclusions in Cu-doped ZnO thin films. Phys Rev B, 2007, 75, 054423 doi: 10.1103/PhysRevB.75.054423[51] Huang J C A, Hsu H S. Inspection of magnetic semiconductor and clustering structure in CoFe-doped ZnO films by bias-dependent impedance spectroscopy. Appl Phys Lett, 2005, 87, 132503 doi: 10.1063/1.2058211[52] Cho Y M, Choo W K, Kim H, et al. Effects of rapid thermal annealing on the ferromagnetic properties of sputtered Zn1– x(Co0.5Fe0.5) xO thin films. Appl Phys Lett, 2002, 80, 3358 doi: 10.1063/1.1478146[53] Karmakar D, Rao T V C, Yakhmi J V, et al. Electronic structure and magnetic properties of (Fe,Co)-codoped ZnO: Theory and experiment. Phys Rev B, 2010, 81, 184421 doi: 10.1103/PhysRevB.81.184421[54] Lisenkov S, Andriotis A N, Sheetz R M, et al. Effects of codoping on the ferromagnetic enhancement in ZnO. Phys Rev B, 2011, 83, 235203 doi: 10.1103/PhysRevB.83.235203[55] Duan L B, Rao G H, Wang Y C, et al. Magnetization and Raman scattering studies of (Co, Mn) codoped ZnO nanoparticles. J Appl Phys, 2008, 104, 013909 doi: 10.1063/1.2952516[56] Coey J M, Venkatesan M, Fitzgerald C B. Donor impurity band exchange in dilute ferromagnetic oxides. Nat Mater, 2005, 4, 173 doi: 10.1038/nmat1310[57] Kaspar T, Droubay T, Heald S, et al. Hidden ferromagnetic secondary phases in cobalt-doped ZnO epitaxial thin films. Phys Rev B, 2008, 77, 201303(R) doi: 10.1103/PhysRevB.77.201303[58] Jedrecy N, Bardeleben H J von, Demaille D. High-temperature ferromagnetism by means of oriented nanocolumns: Co clustering in (Zn,Co)O. Phys Rev B, 2009, 80, 205204 doi: 10.1103/PhysRevB.80.205204[59] Zhu D, Liu G, Tian Y, et al. Decoupled scenario between the conductive carriers and the ferromagnetism in epitaxial Zn0.85– xMg xCo0.15O thin films. Appl Phys Lett, 2014, 105, 072404 doi: 10.1063/1.4893563[60] Chiou J W, Tsai H M, Pao C W, et al. Role of valence-band Co 3d states on ferromagnetism in Zn1– xCo xO nanorods. Appl Phys Lett, 2007, 90, 062103 doi: 10.1063/1.2432234[61] Kobayashi M, Ishida Y, Hwang J, et al. Characterization of magnetic components in the diluted magnetic semiconductor Zn1– xCo xO by X-ray magnetic circular dichroism. Phys Rev B, 2005, 72, 201201 doi: 10.1103/PhysRevB.72.201201[62] Editorial. More than just room temperature. Nat Mater, 2010, 9, 951 doi: 10.1038/nmat2918[63] Zunger A, Lany S, Raebiger H. The quest for dilute ferromagnetism in semiconductors: Guides and misguides by theory. Physics, 2010, 3, 53 doi: 10.1103/Physics.3.53[64] Chang C Z, Feng X, Shen J, et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science, 2013, 340, 167 doi: 10.1126/science.1234414[65] Wang Z, Tang C, Sachs R, et al. Proximity-induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys Rev Lett, 2015, 114, 016603 doi: 10.1103/PhysRevLett.114.016603[66] Zhou J, Wang Q, Sun Q, et al. Ferromagnetism in semihydrogenated graphene sheet. Nano Lett, 2009, 9, 3867 doi: 10.1021/nl9020733[67] Soriano D, Leconte N, Ordejón P, et al. Magnetoresistance and magnetic ordering fingerprints in hydrogenated graphene. Phys Rev Lett, 2011, 107, 016602 doi: 10.1103/PhysRevLett.107.016602[68] Uchoa B, Kotov V N, Peres N M R, et al. Localized magnetic states in graphene. Phys Rev Lett, 2008, 101, 026805 doi: 10.1103/PhysRevLett.101.026805[69] Yazyev O V. Magnetism in disordered graphene and irradiated graphite. Phys Rev Lett, 2008, 101, 037203 doi: 10.1103/PhysRevLett.101.037203[70] Faccio R, Pardo H, Denis P A, et al. Magnetism induced by single carbon vacancies in a three-dimensional graphitic network. Phys Rev B, 2008, 77, 035416 doi: 10.1103/PhysRevB.77.035416[71] Castro E V, Peres N M R, Stauber T, et al. Low-density ferromagnetism in biased bilayer graphene. Phys Rev Lett, 2008, 100, 186803 doi: 10.1103/PhysRevLett.100.186803[72] Wang Y, Huang Y, Song Y, et al. Room-temperature ferromagnetism of graphene. Nano Lett, 2009, 9, 220 doi: 10.1021/nl802810g[73] Matte H S S R, Subrahmanyam K S, Rao C N R. Novel magnetic properties of graphene: presence of both ferromagnetic and antiferromagnetic features and other aspects. J Phys Chem C, 2009, 113, 9982 doi: 10.1021/jp903397u[74] Xie L, Wang X, Lu J, et al. Room temperature ferromagnetism in partially hydrogenated epitaxial graphene. Appl Phys Lett, 2011, 98, 193113 doi: 10.1063/1.3589970[75] Candini A, Alvino C, Wernsdorfer W, et al. Hysteresis loops of magnetoconductance in graphene devices. Phys Rev B, 2011, 83, 121401 doi: 10.1103/PhysRevB.83.121401[76] Sepioni M, Nair R R, Rablen S, et al. Limits on intrinsic magnetism in graphene. Phys Rev Lett, 2010, 105, 207205 doi: 10.1103/PhysRevLett.105.207205[77] Nair R R, Sepioni M, Tsai I L, et al. Spin-half paramagnetism in graphene induced by point defects. Nat Phys, 2012, 8, 199 doi: 10.1038/nphys2183[78] Zhang H, Chhowalla M, Liu Z. 2D nanomaterials: graphene and transition metal dichalcogenides. Chem Soc Rev, 2018, 47, 3015 doi: 10.1039/C8CS90048E[79] Wang X, Song Z, Wen W, et al. Potential 2D materials with phase transitions: structure, synthesis, and device applications. Adv Mater, 2018, 1804682 doi: 10.1002/adma.201804682[80] Shi J, Hong M, Zhang Z, et al. Physical properties and potential applications of two-dimensional metallic transition metal dichalcogenides. Coord Chem Rev, 2018, 376, 1 doi: 10.1016/j.ccr.2018.07.019[81] Ramasubramaniam A, Naveh D. Mn-doped monolayer MoS2: An atomically thin dilute magnetic semiconductor. Phys Rev B, 2013, 87, 195201 doi: 10.1103/PhysRevB.87.195201[82] Mishra R, Zhou W, Pennycook S J, et al. Long-range ferromagnetic ordering in manganese-doped two-dimensional dichalcogenides. Phys Rev B, 2013, 88, 144409 doi: 10.1103/PhysRevB.88.144409[83] Sun L, Zhou W, Liang Y, et al. Magnetic properties in Fe-doped SnS2: Density functional calculations. Comput Mater Sci, 2016, 117, 489 doi: 10.1016/j.commatsci.2016.02.028[84] Seixas L, Carvalho A, Neto A H Castro. Atomically thin dilute magnetism in Co-doped phosphorene. Phys Rev B, 2015, 91, 155138 doi: 10.1103/PhysRevB.91.155138[85] Li B, Xing T, Zhong M, et al. A two-dimensional Fe-doped SnS2 magnetic semiconductor. Nat Commun, 2017, 8, 1958 doi: 10.1038/s41467-017-02077-z[86] Gong C, Li L, Li Z, et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature, 2017, 546, 265 doi: 10.1038/nature22060[87] Huang B, Clark G, Moratalla N, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature, 2017, 546, 270 doi: 10.1038/nature22391[88] Griffiths R B. Peierls proof of spontaneous magnetization in a two-dimensional ising ferromagnet. Phys Rev, 1964, 136, A437 doi: 10.1103/PhysRev.136.A437[89] Mermin N D, Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic heisenberg models. Phys Rev Lett, 1966, 17, 1133 doi: 10.1103/PhysRevLett.17.1133[90] Wang Z, Zhang T, Ding M, et al. Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat Nanotechnol, 2018, 13, 554 doi: 10.1038/s41565-018-0186-z[91] Jiang S, Shan J, Mak K F. Electric-field switching of two-dimensional van der Waals magnets. Nat Mater, 2018, 17, 406 doi: 10.1038/s41563-018-0040-6[92] Jiang S, Li L, Wang Z, et al. Controlling magnetism in 2D CrI3 by electrostatic doping. Nat Nanotechnol, 2018, 13, 549 doi: 10.1038/s41565-018-0135-x[93] Huang B, Clark G, Klein D R, et al. Electrical control of 2D magnetism in bilayer CrI3. Nat Nanotechnol, 2018, 13, 544 doi: 10.1038/s41565-018-0121-3[94] Anderson P W. Localized magnetic states in metals. Phys Rev, 1961, 124, 41 doi: 10.1103/PhysRev.124.41[95] Schrieffer J R, Wolff P A. Relation between the Anderson and Kondo Hamiltonians. Phys Rev, 1966, 149, 491 doi: 10.1103/PhysRev.149.491[96] MacDonald A H, Schiffer P, Samarth N. Ferromagnetic semiconductors: moving beyond (Ga,Mn)As. Nat Mater, 2005, 4, 195 doi: 10.1038/nmat1325[97] Zeng Y J, Gauquelin N, Li D Y, et al. Co-rich ZnCoO nanoparticles embedded in wurtzite Zn1– xCo xO thin films: possible origin of superconductivity. ACS Appl Mater Interfaces, 2015, 7, 22166 doi: 10.1021/acsami.5b06363[98] Akaiwa K, Kaneko K, Fujita S, et al. Room temperature ferromagnetism in conducting α-(In1– xFe x)2O3 alloy films. Appl Phys Lett, 2015, 106, 062405 doi: 10.1063/1.4908050[99] Tu N T, Hai P N, Anh L D, et al. Magnetic properties and intrinsic ferromagnetism in (Ga,Fe)Sb ferromagnetic semiconductors. Phys Rev B, 2015, 92, 144403 doi: 10.1103/PhysRevB.92.144403[100] Li L, Guo Y, Cui X Y, et al. Magnetism of Co-doped ZnO epitaxially grown on a ZnO substrate. Phys Rev B, 2012, 85, 174430 doi: 10.1103/PhysRevB.85.174430[101] Cao Q, Zhu D, Fu M, et al. Robust ferromagnetism of single crystalline Co xZn1– xO (0.3 ≤ x ≤ 0.45) epitaxial films with high Co concentration. Appl Phys Lett, 2016, 109, 052404 doi: 10.1063/1.4960555[102] Cao Q, Fu M, Zhu D, et al. Enhancing s, p-d exchange interactions at room temperature by carrier doping in single crystalline Co0.4Zn0.6O epitaxial films. Appl Phys Lett, 2017, 110, 092402 doi: 10.1063/1.4977765[103] Cao Q, Fu M, Zhu D, et al. Growth-controlled engineering of magnetic exchange interactions in single crystalline GaCo- ZnO1-v epitaxial films with high Co concentration. Chem Mater, 2017, 29, 2717 doi: 10.1021/acs.chemmater.6b03339[104] Redman M J, Steward E G. Cobaltous oxide with the zinc blende/wurtzite-type crystal structure. Nature, 1962, 193, 867 doi: 10.1038/193867a0[105] Yan S S, Ren C, Wang X, et al. Ferromagnetism and magnetoresistance of Co–ZnO inhomogeneous magnetic semiconductor. Appl Phys Lett, 2004, 84, 2376 doi: 10.1063/1.1690881[106] Song H Q, Mei L M, Yan S S, et al. Microstructure, ferromagnetism, and magnetic transport of Ti1– xCo xO2 amorphous magnetic semiconductor. J Appl Phys, 2006, 99, 123903 doi: 10.1063/1.2204758[107] Yan S S, Liu J P, Mei L M, et al. Spin-dependent variable range hopping and magnetoresistance in Ti1– xCo xO2 and Zn1– xCo xO magnetic semiconductor films. J Phys: Condens Matter, 2006, 18, 10469 doi: 10.1088/0953-8984/18/46/014[108] Tian Y F, Yan S S, Zhao M W, et al. Controllable spin- polarized electrical transport in wide-band-gap oxide ferromagnetic semiconductors. J Appl Phys, 2010, 107, 033713 doi: 10.1063/1.3305457 -
Proportional views





 DownLoad:
DownLoad: