| Citation: |
Xian Zhang, Xiaodong Cao, Xuelian Zhang. A 16-bit 1 MSPS SAR ADC with foreground calibration and residual voltage shift strategy[J]. Journal of Semiconductors, 2020, 41(12): 122401. doi: 10.1088/1674-4926/41/12/122401
X Zhang, X D Cao, X L Zhang, A 16-bit 1 MSPS SAR ADC with foreground calibration and residual voltage shift strategy[J]. J. Semicond., 2020, 41(12): 122401. doi: 10.1088/1674-4926/41/12/122401.
Export: BibTex EndNote
|
A 16-bit 1 MSPS SAR ADC with foreground calibration and residual voltage shift strategy
doi: 10.1088/1674-4926/41/12/122401
More Information-
Abstract
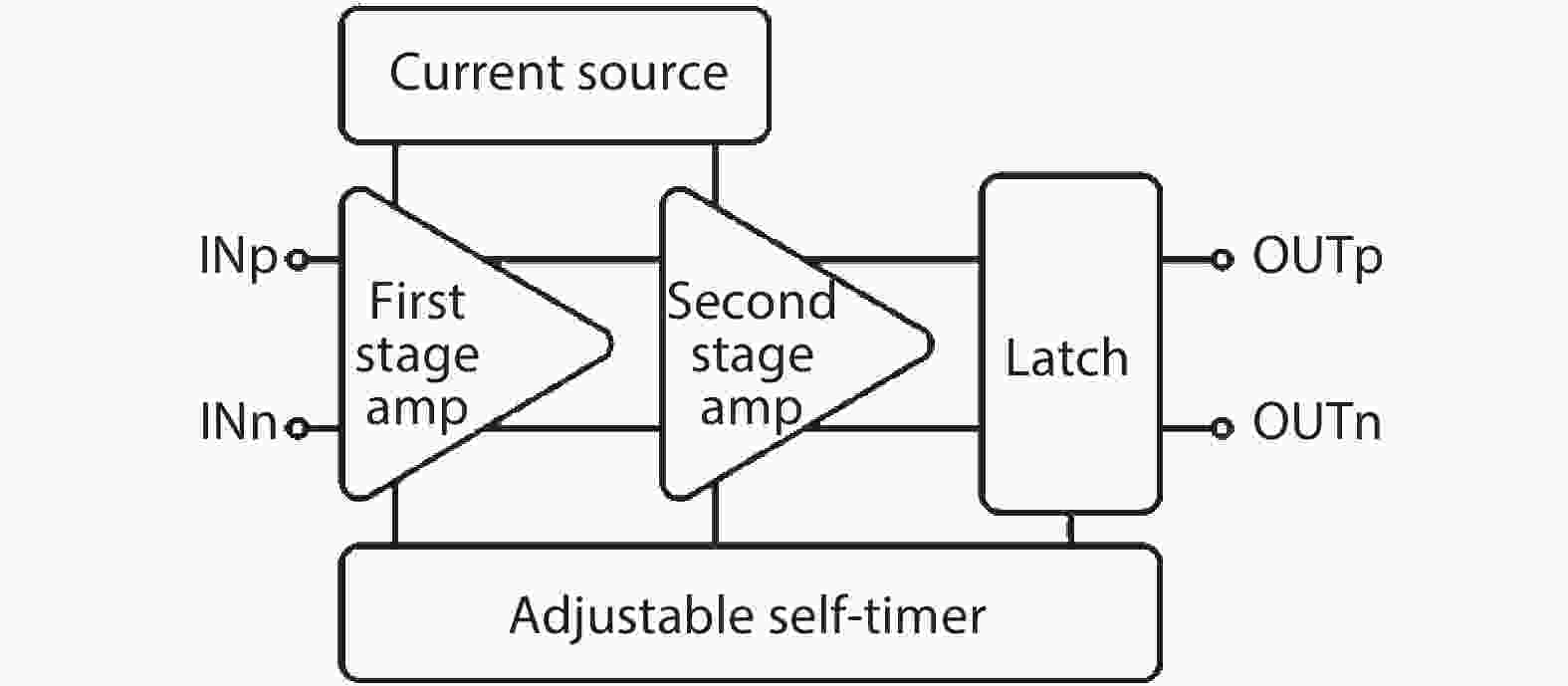
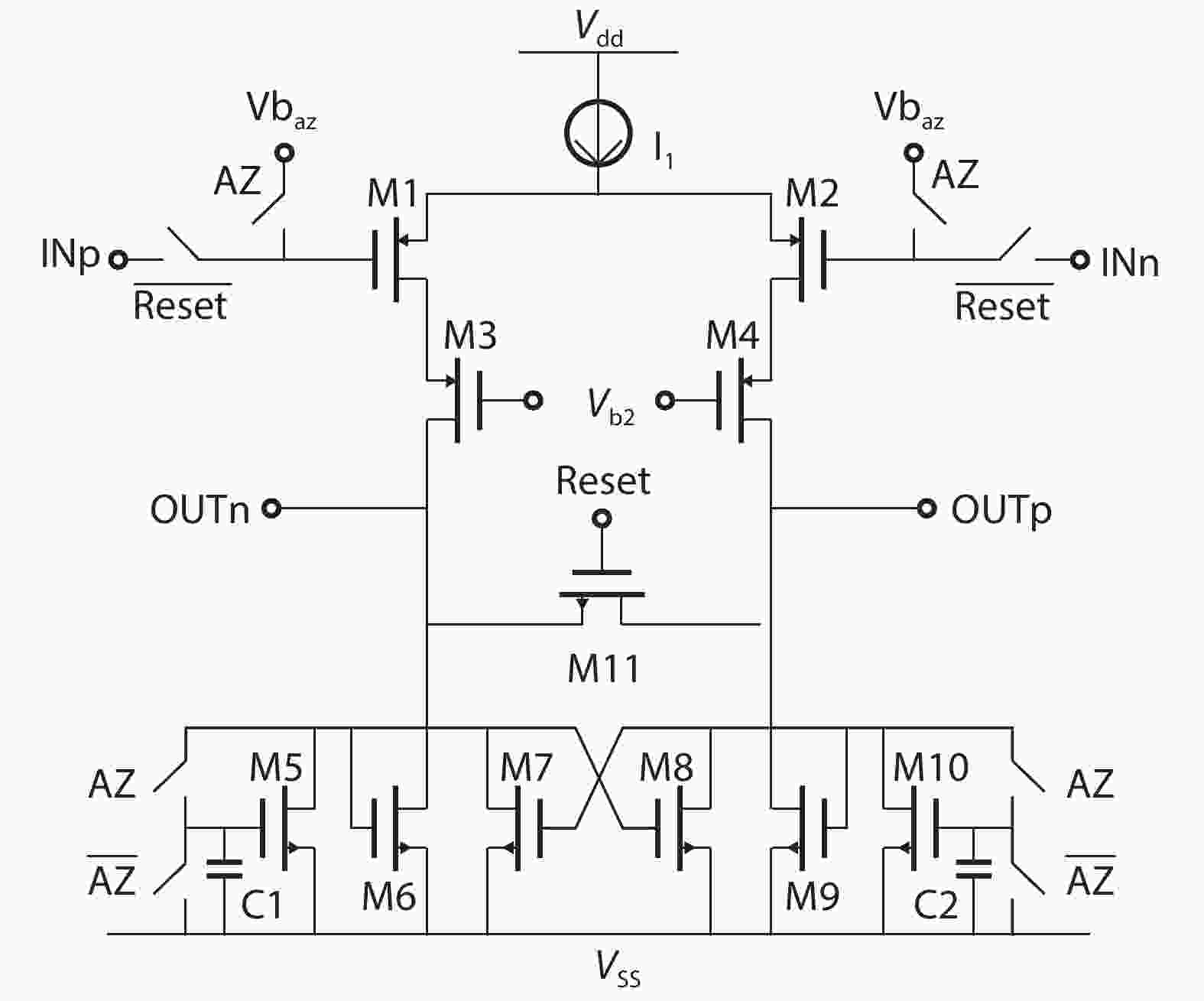
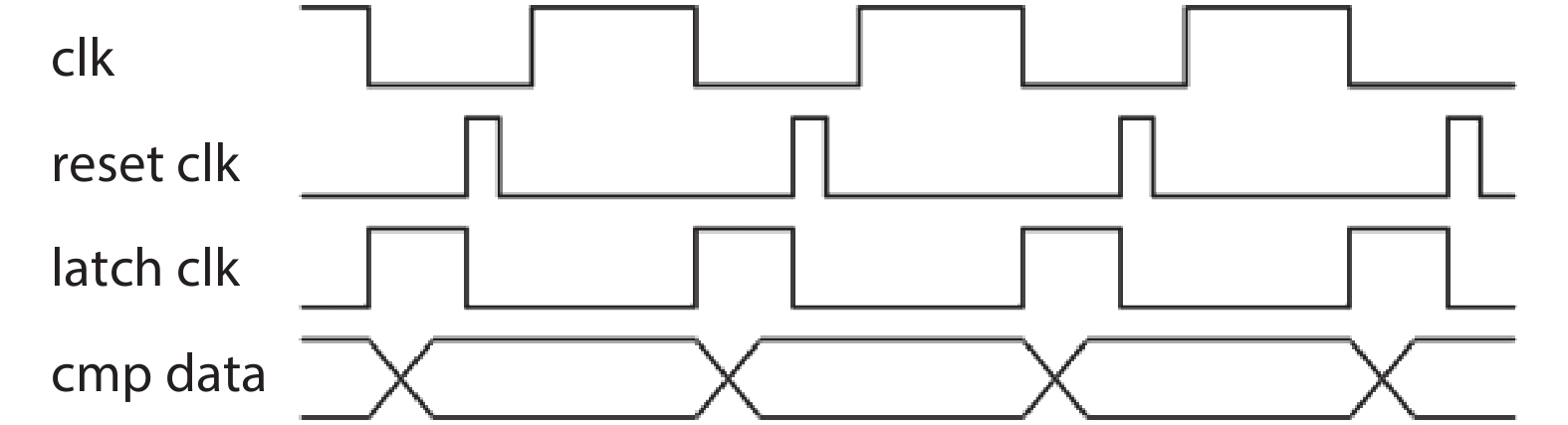
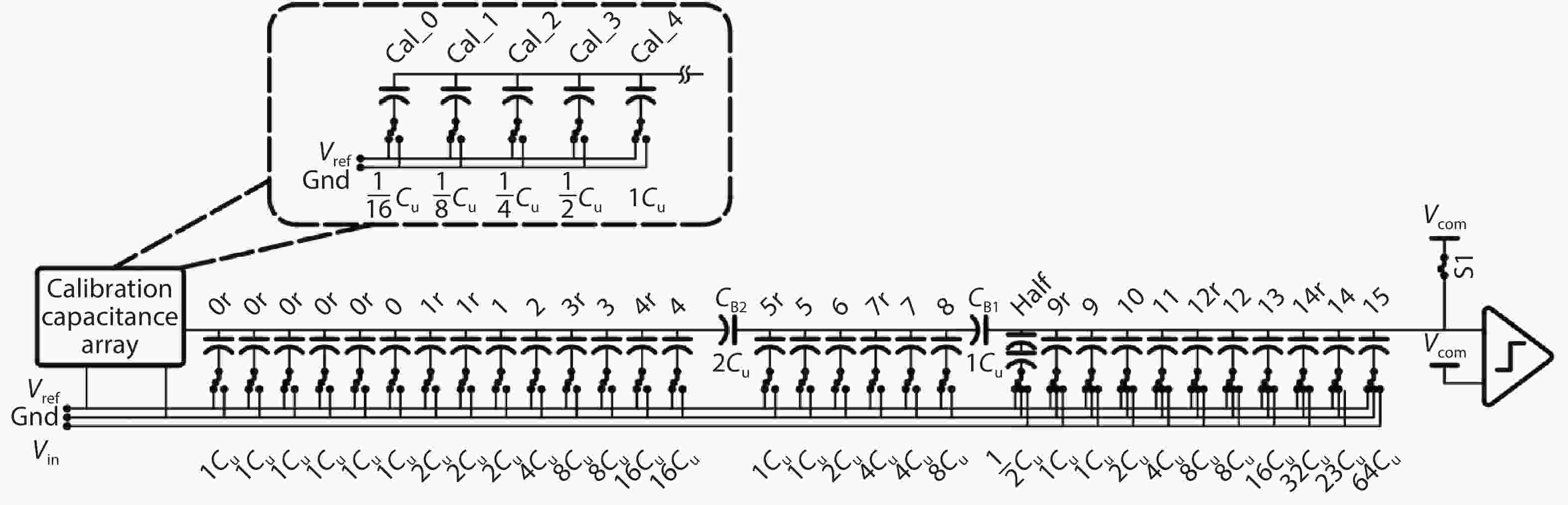
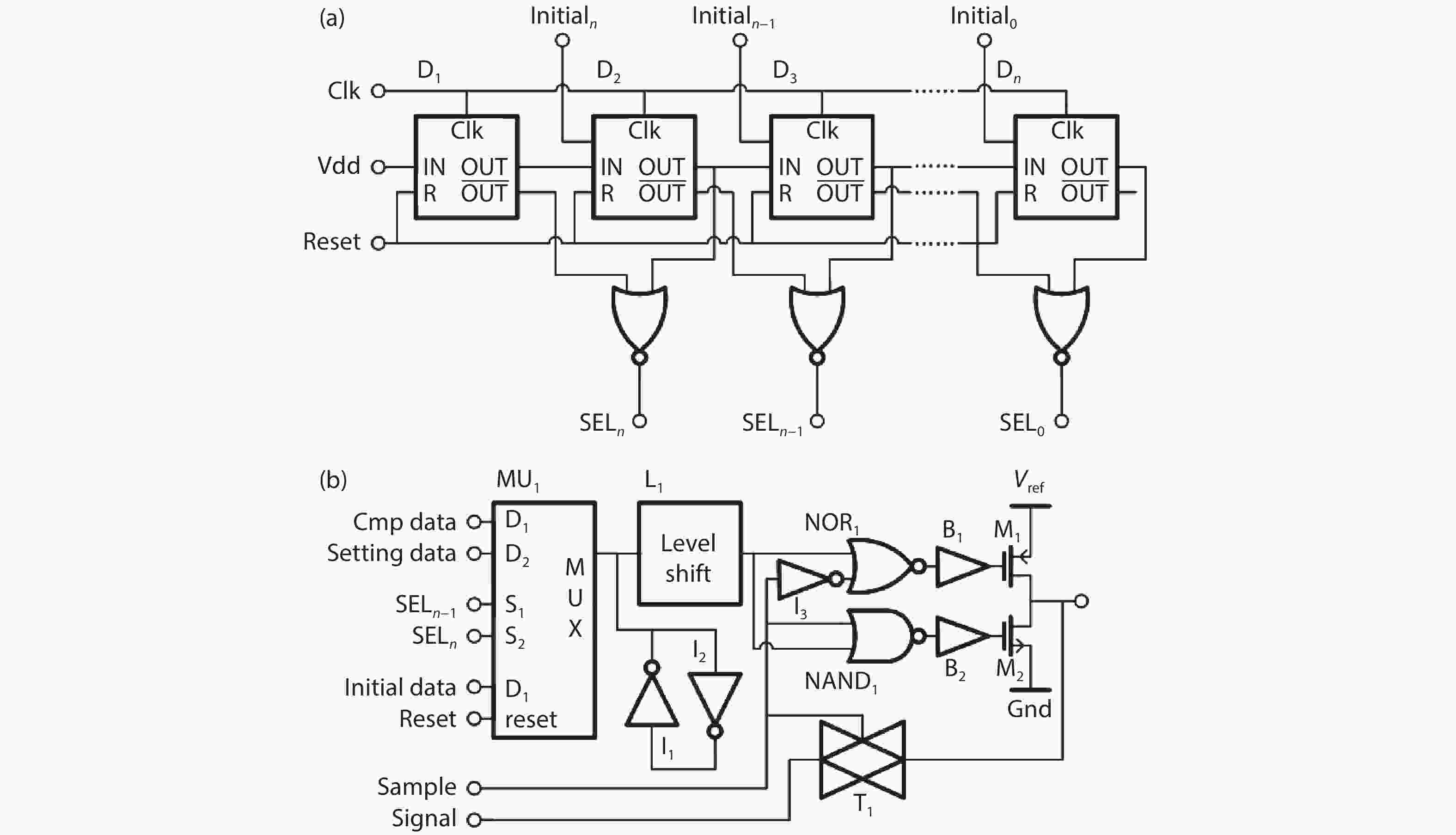
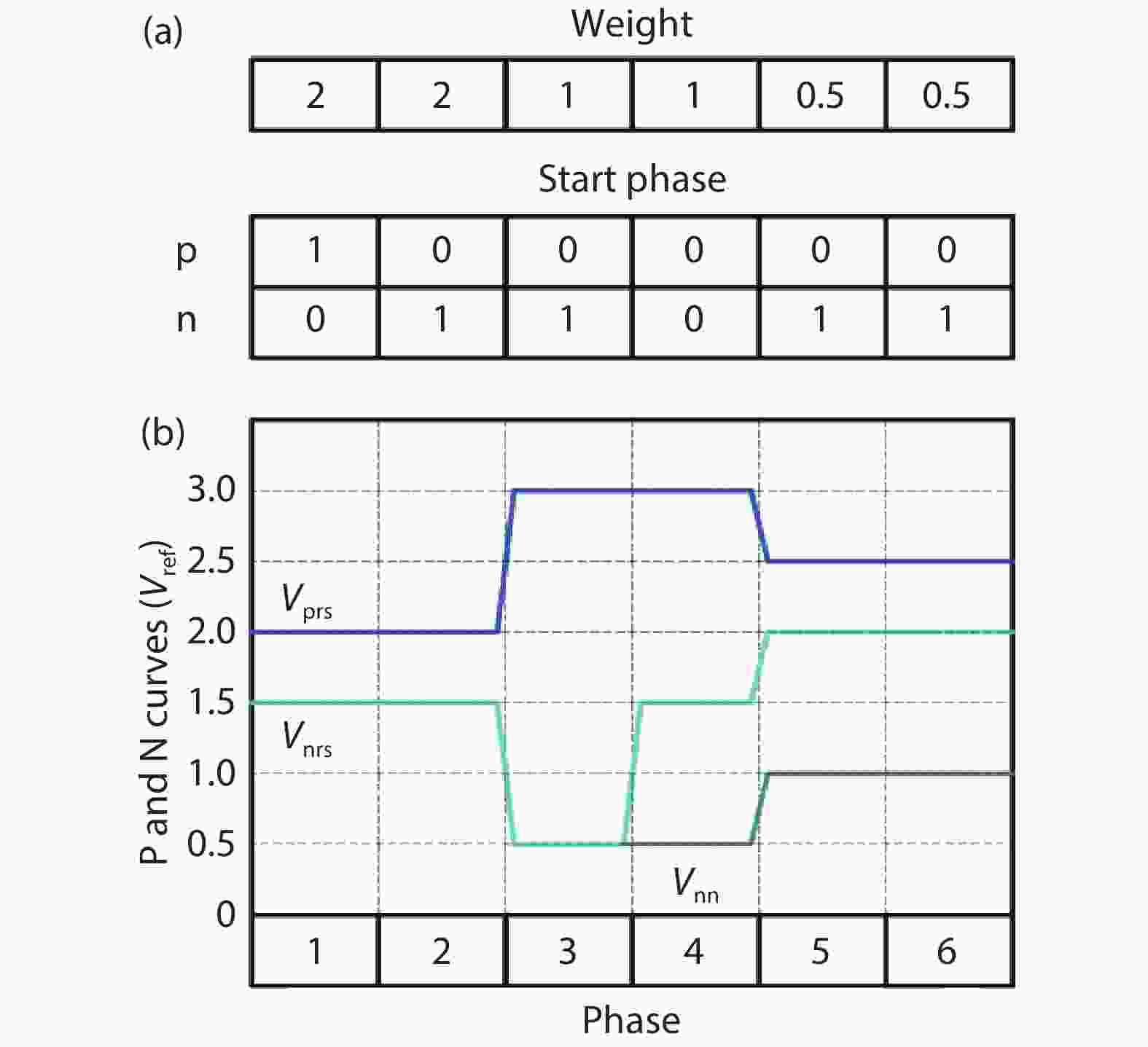
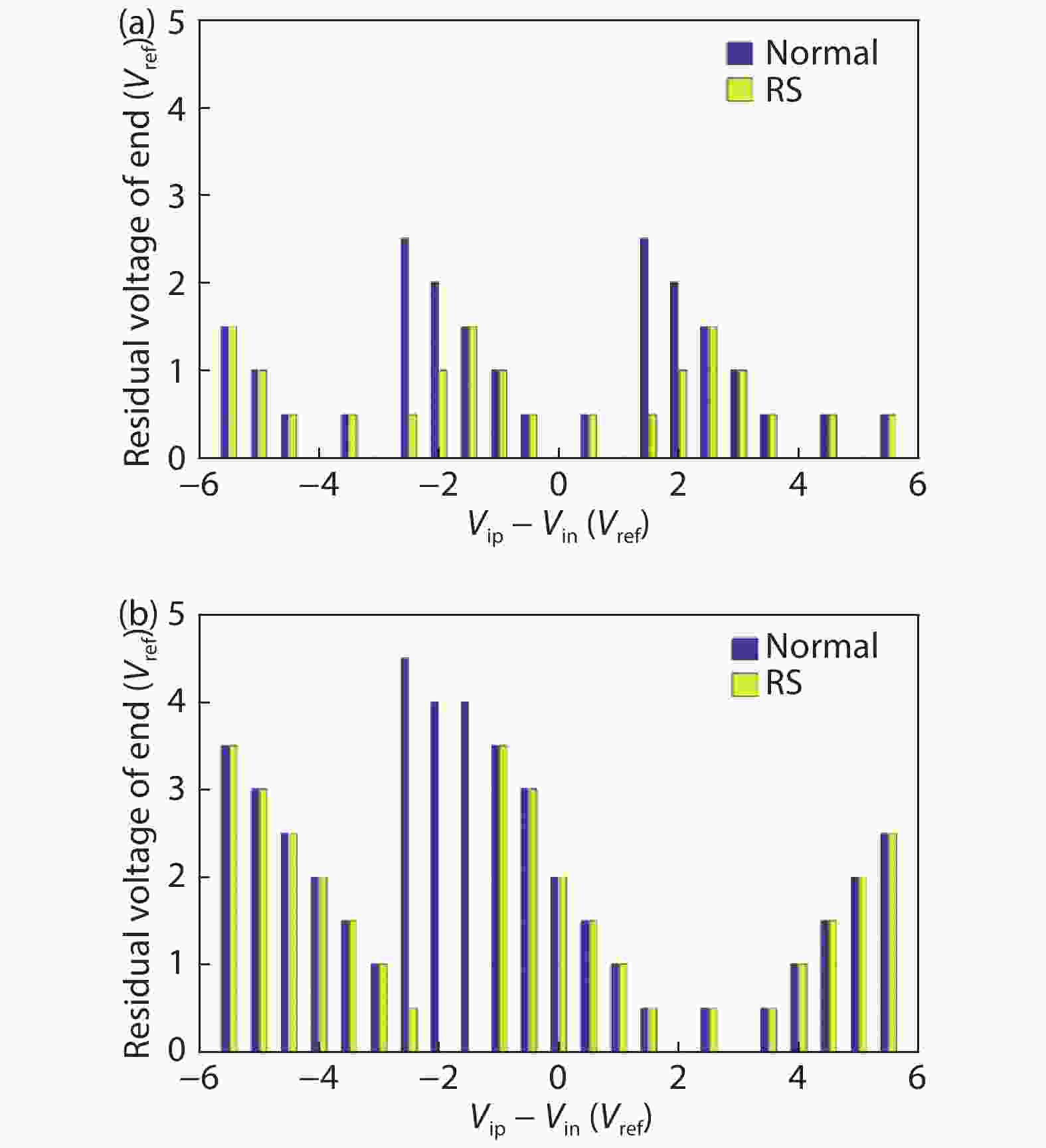
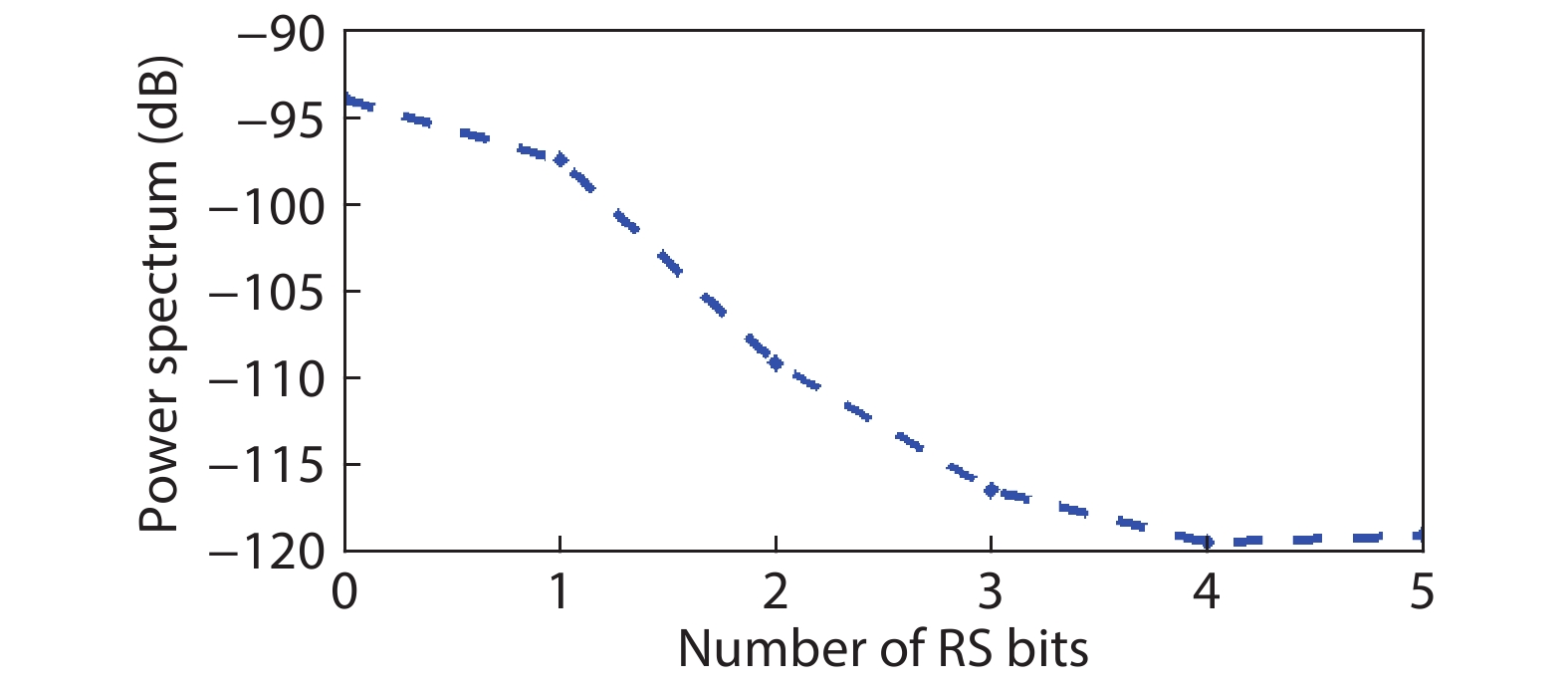
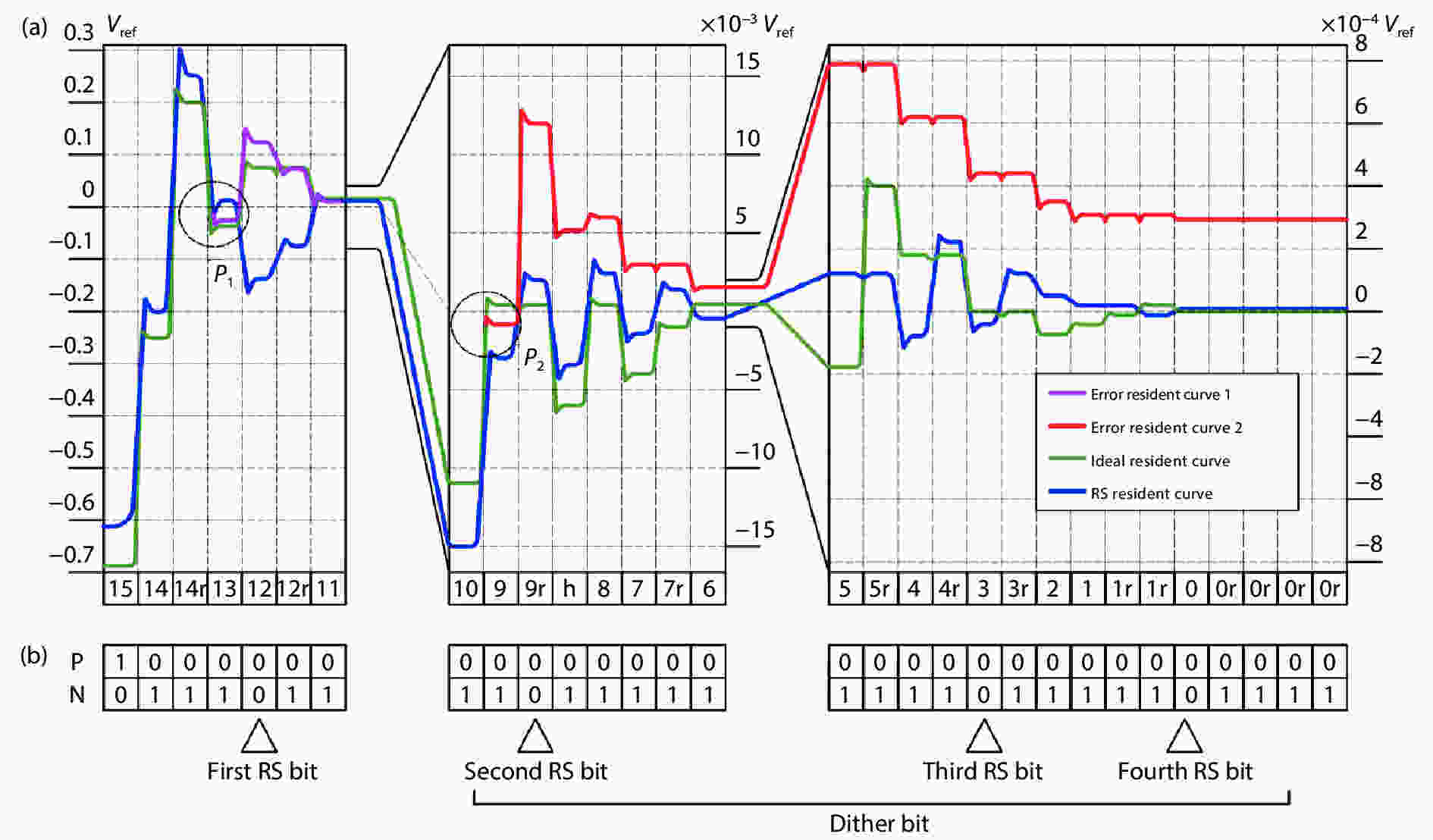
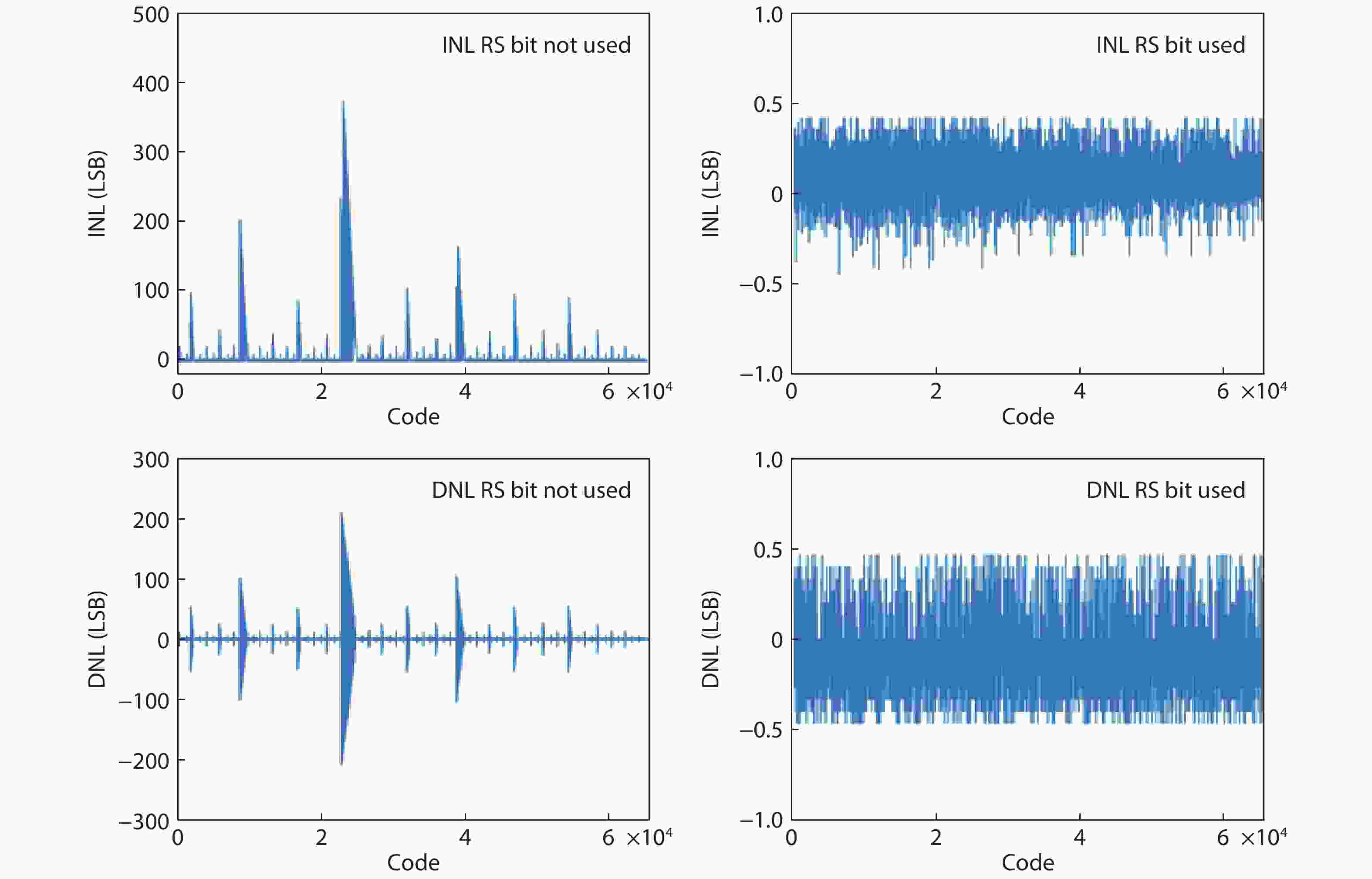
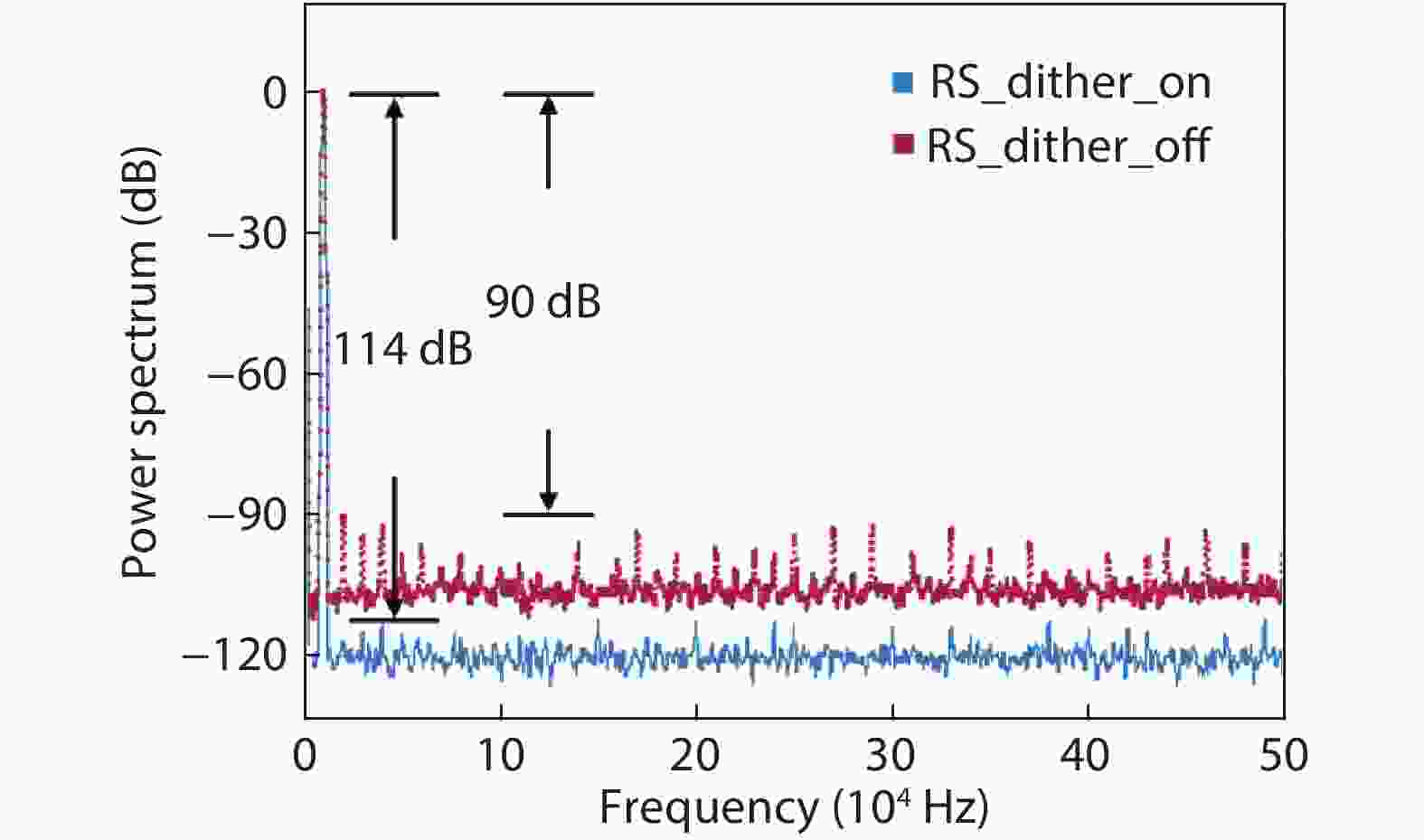
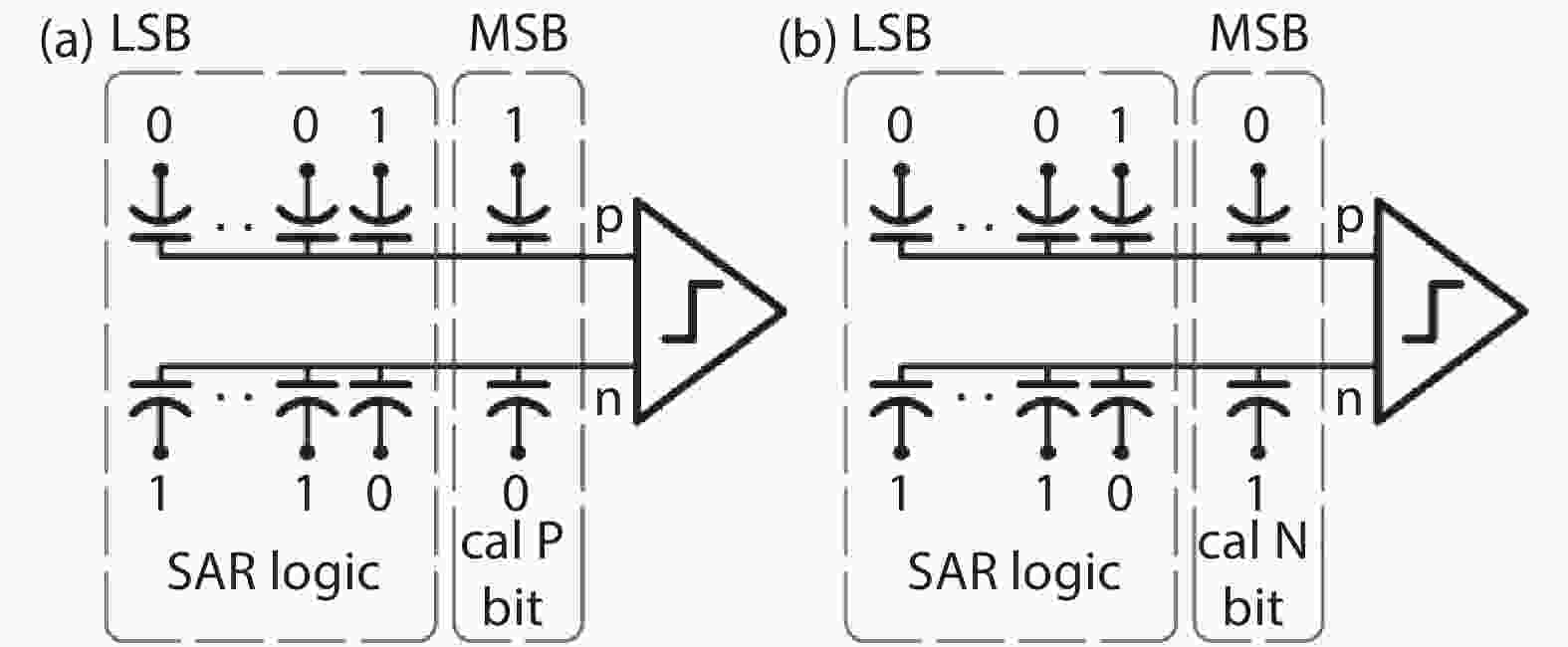
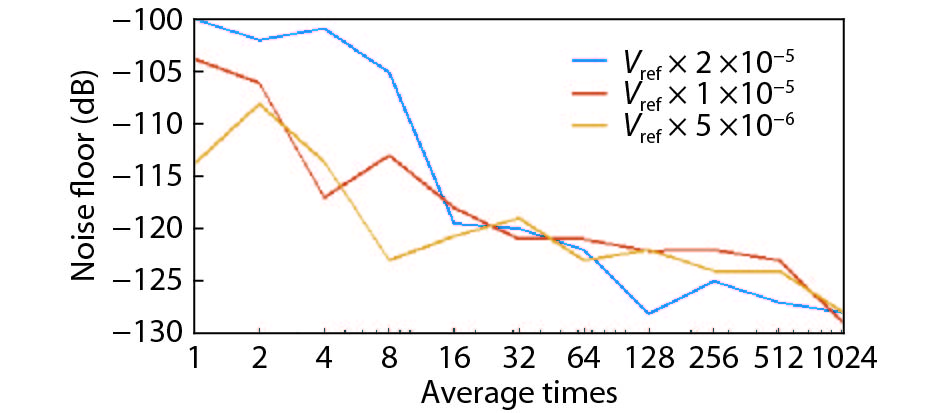
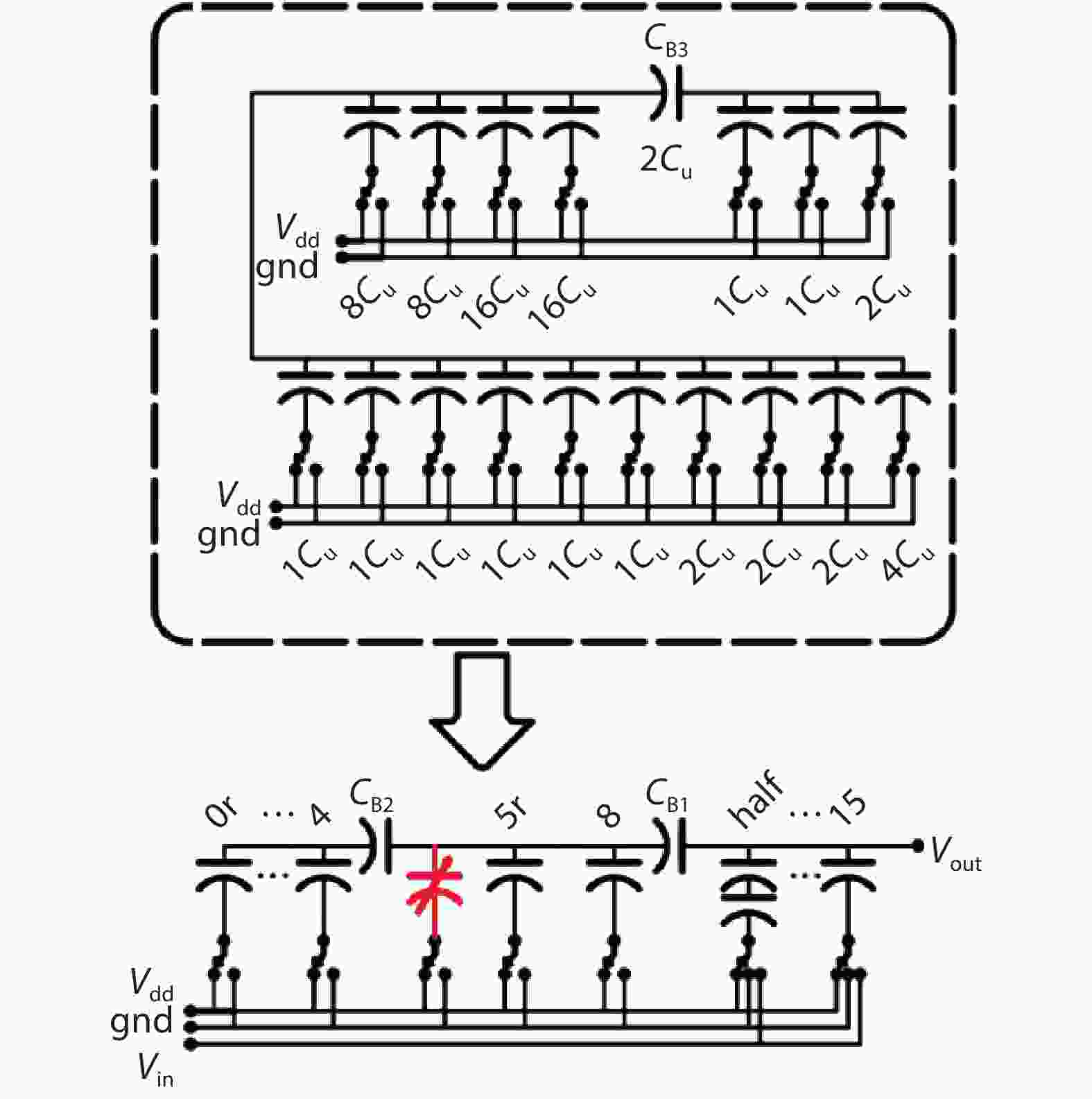
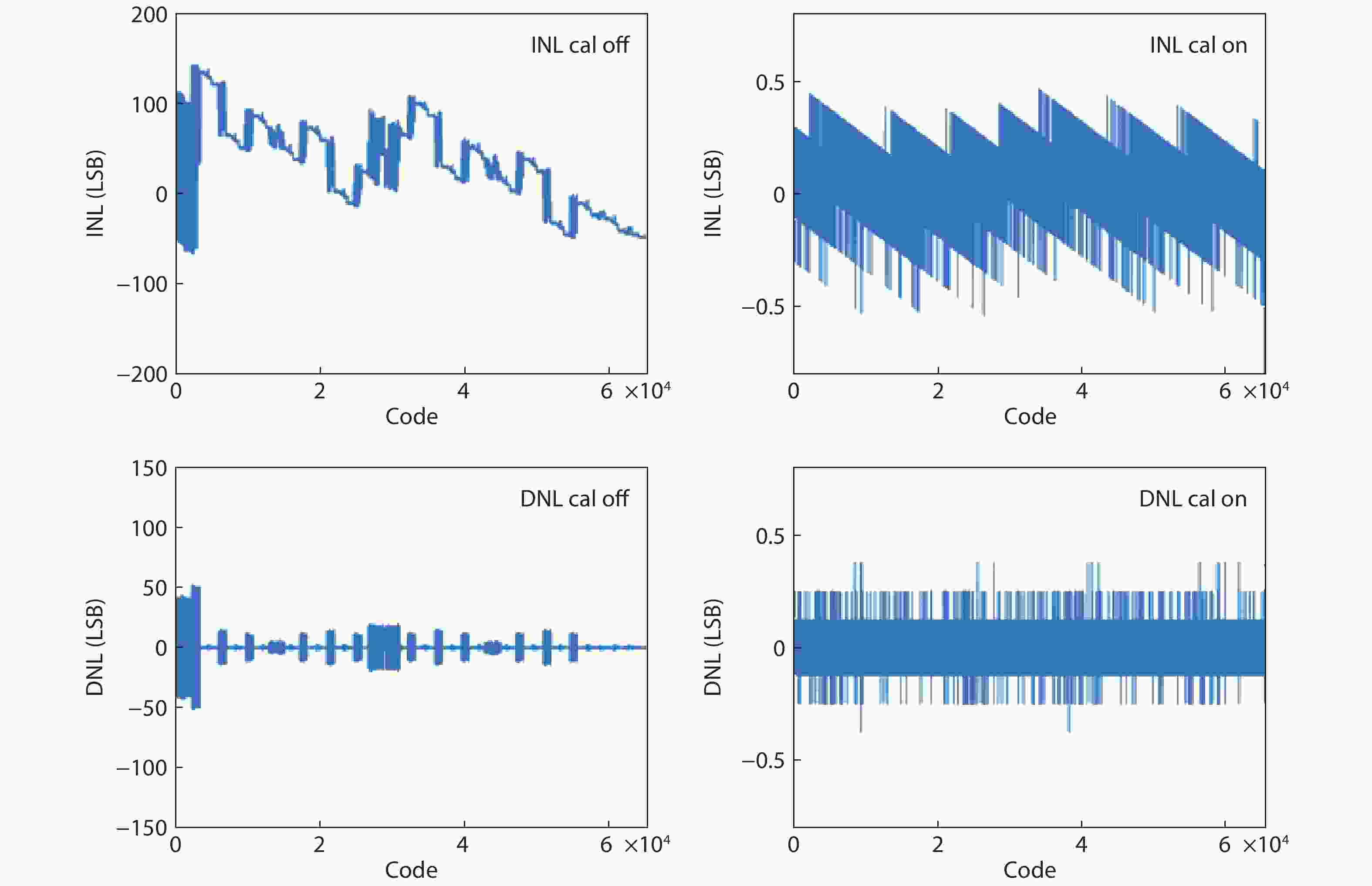
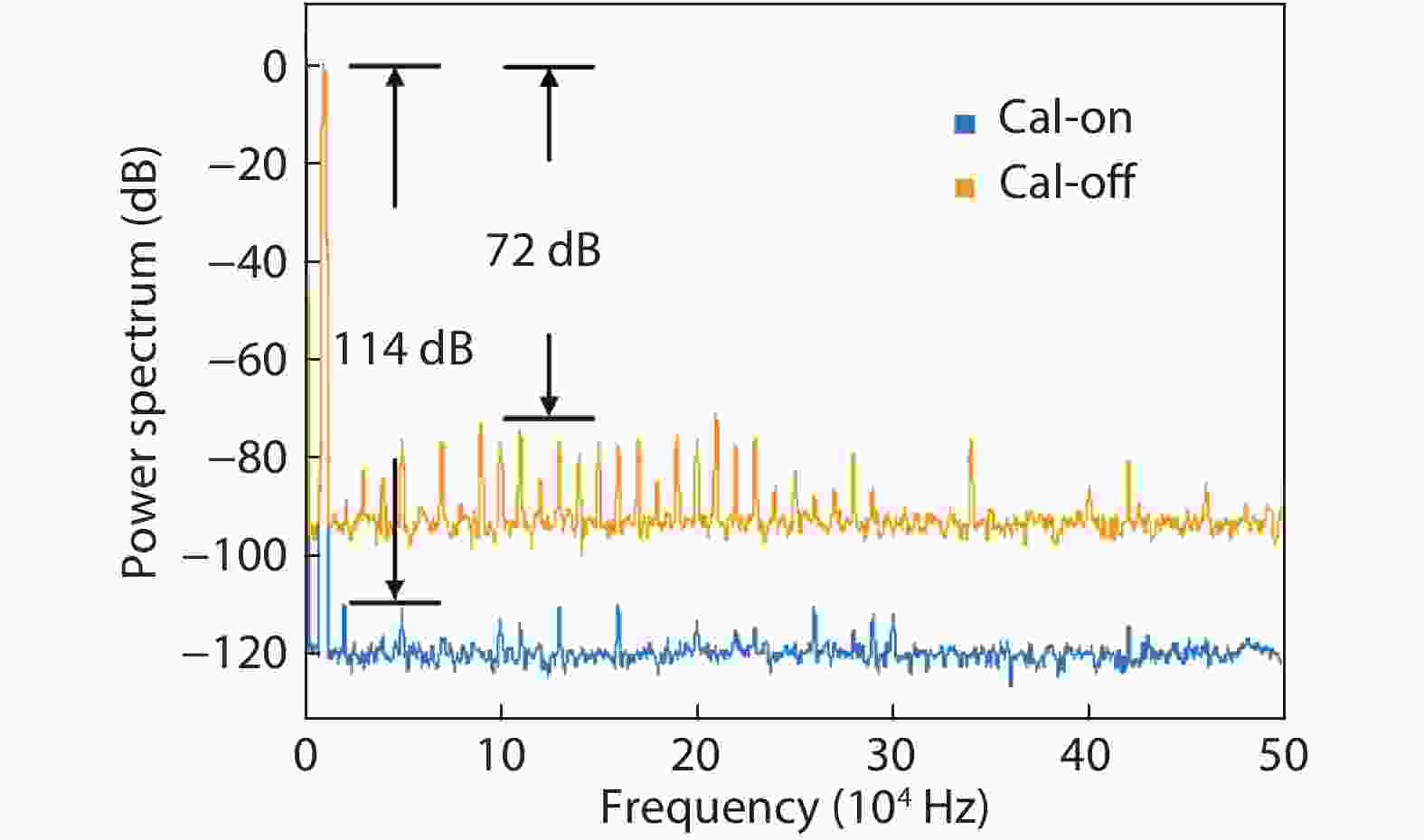
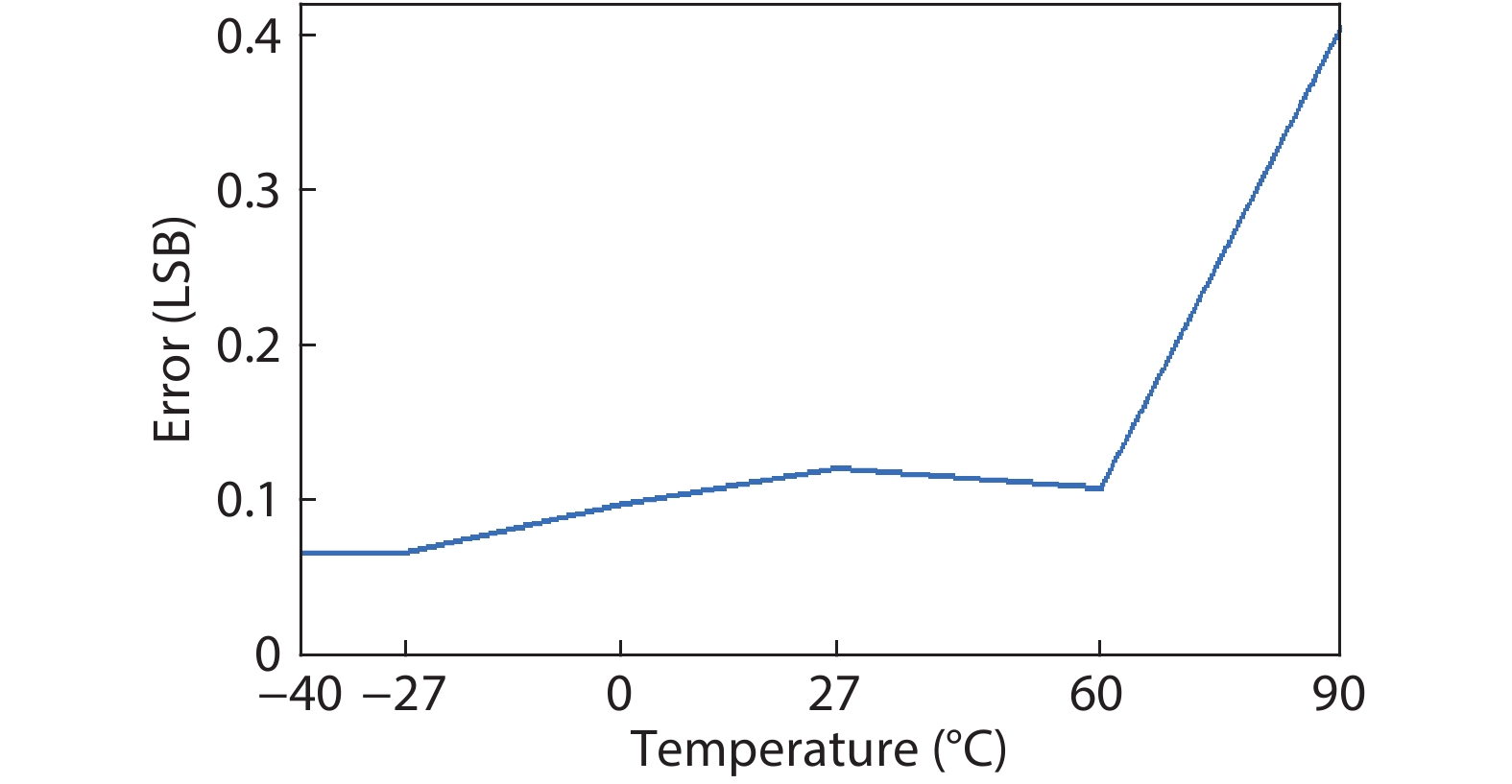
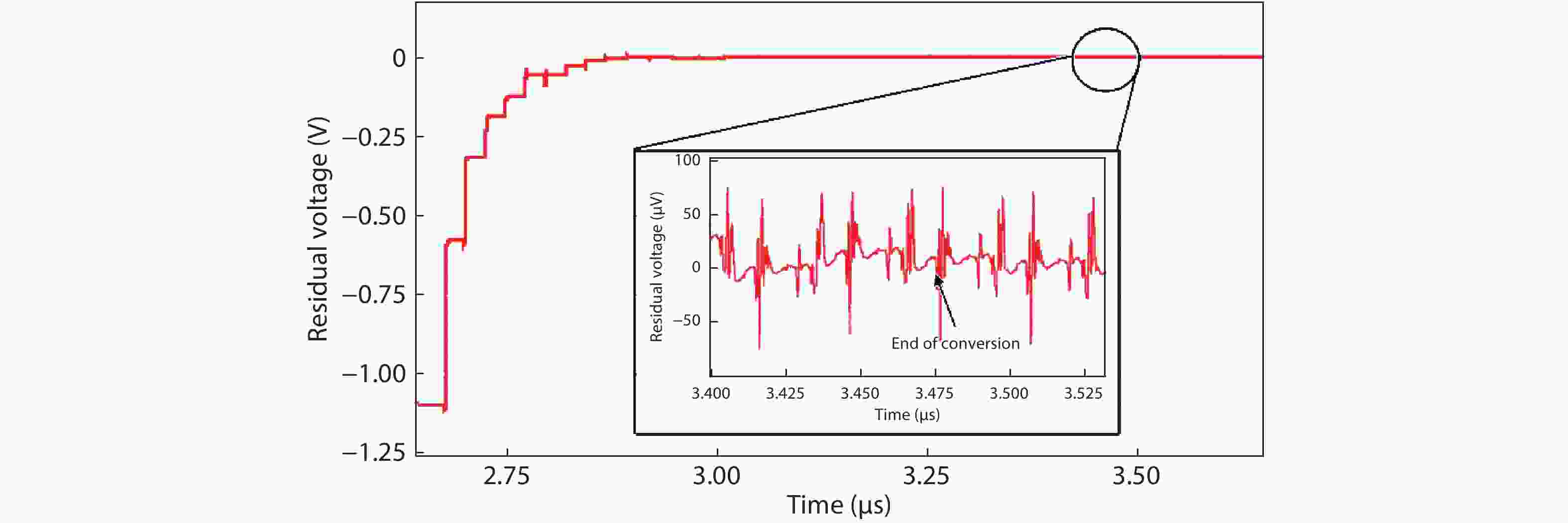
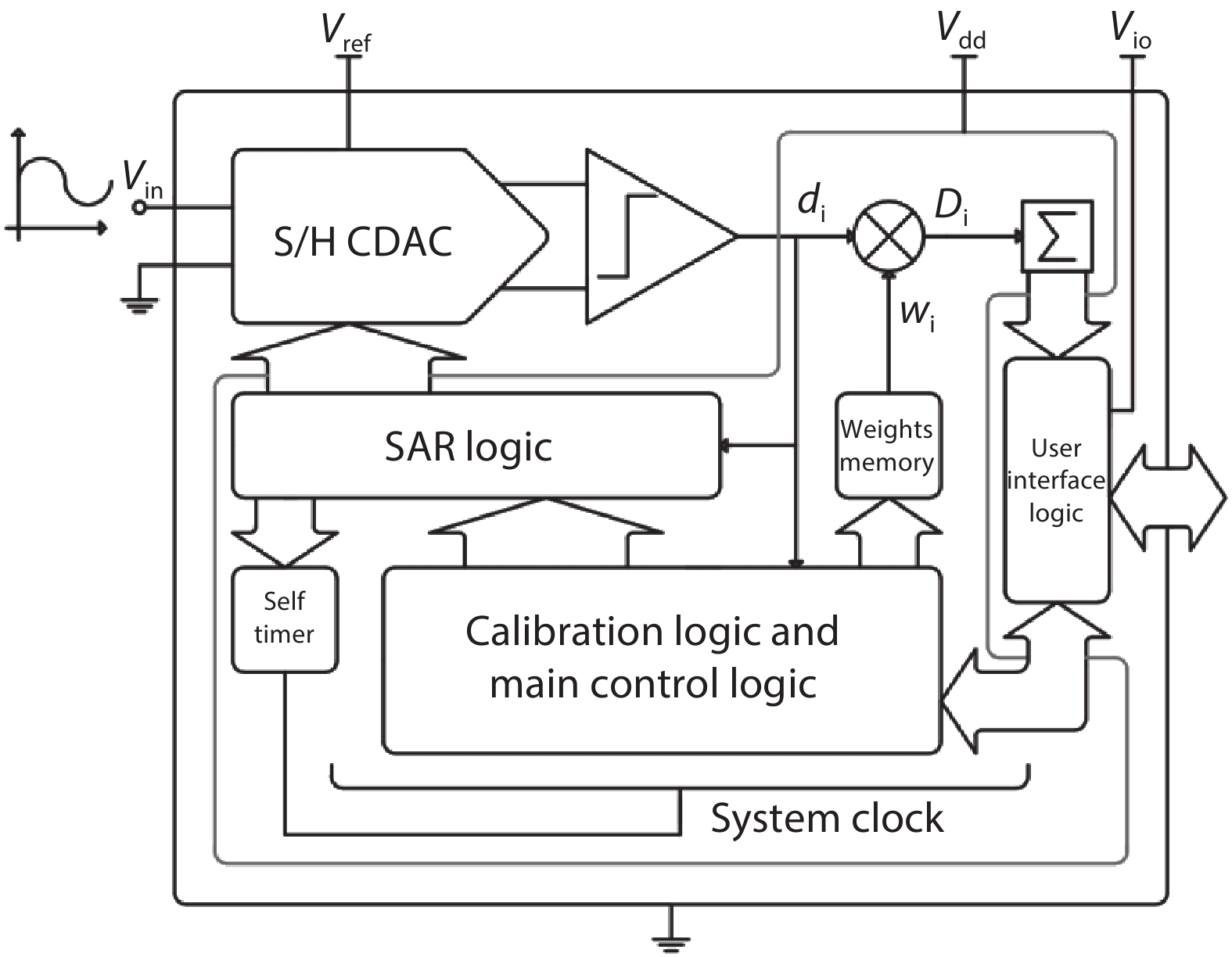
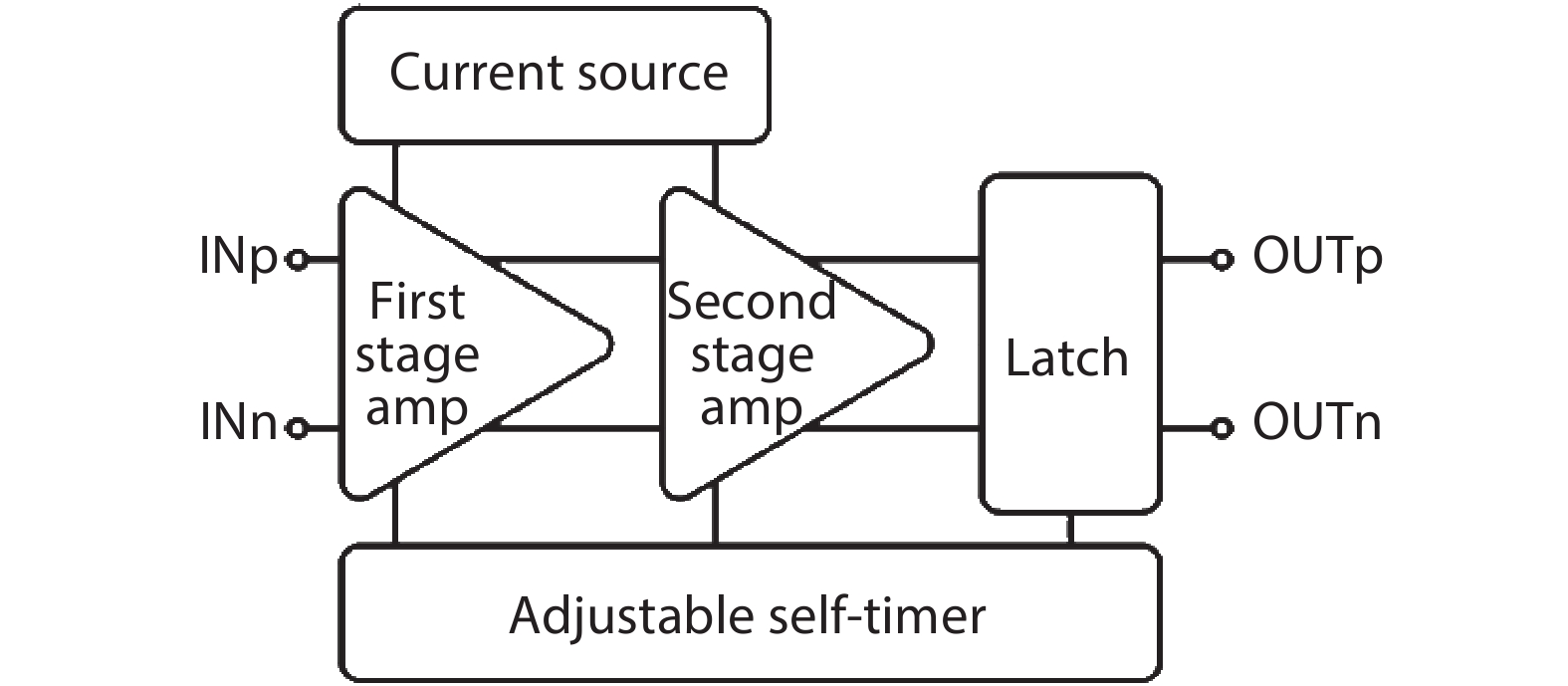
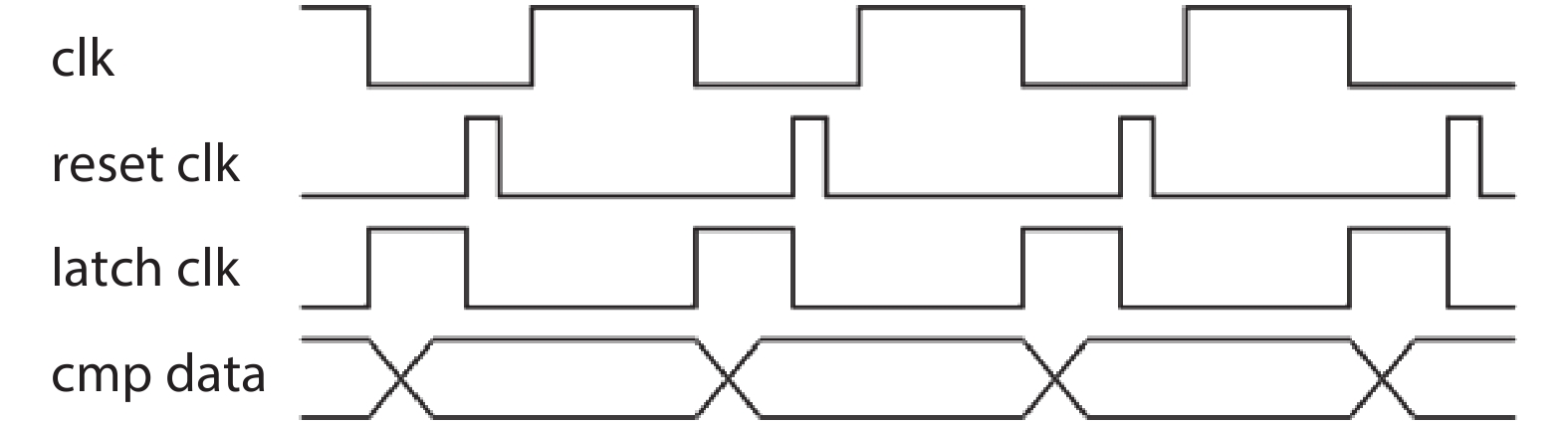
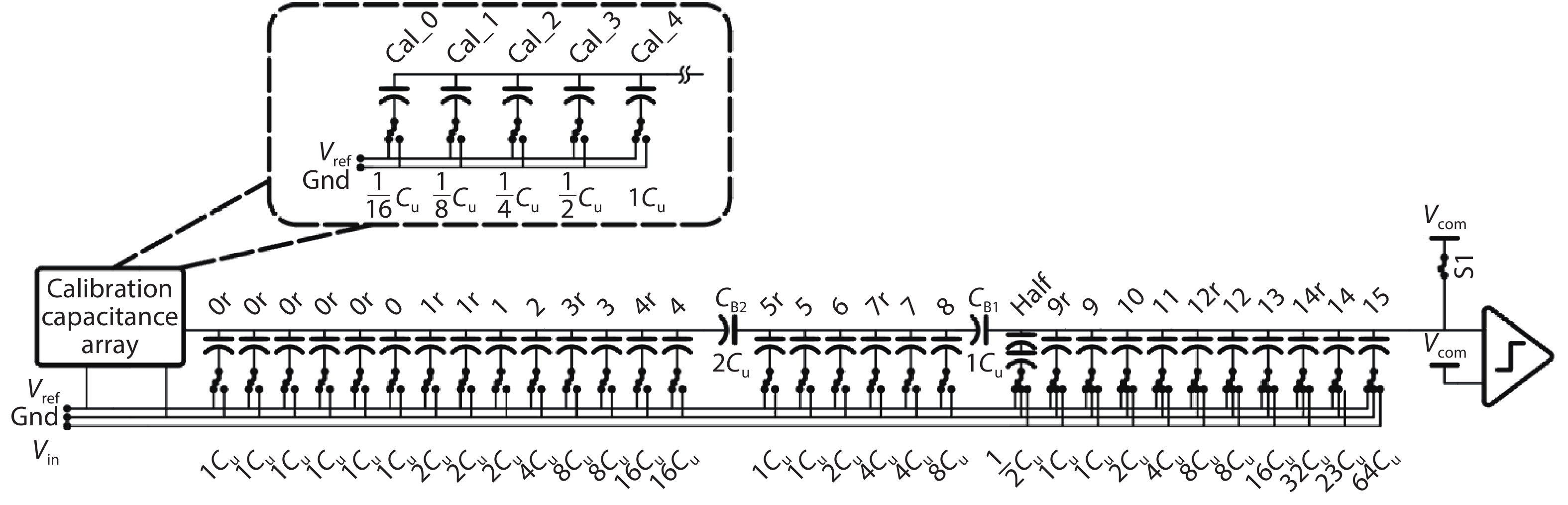
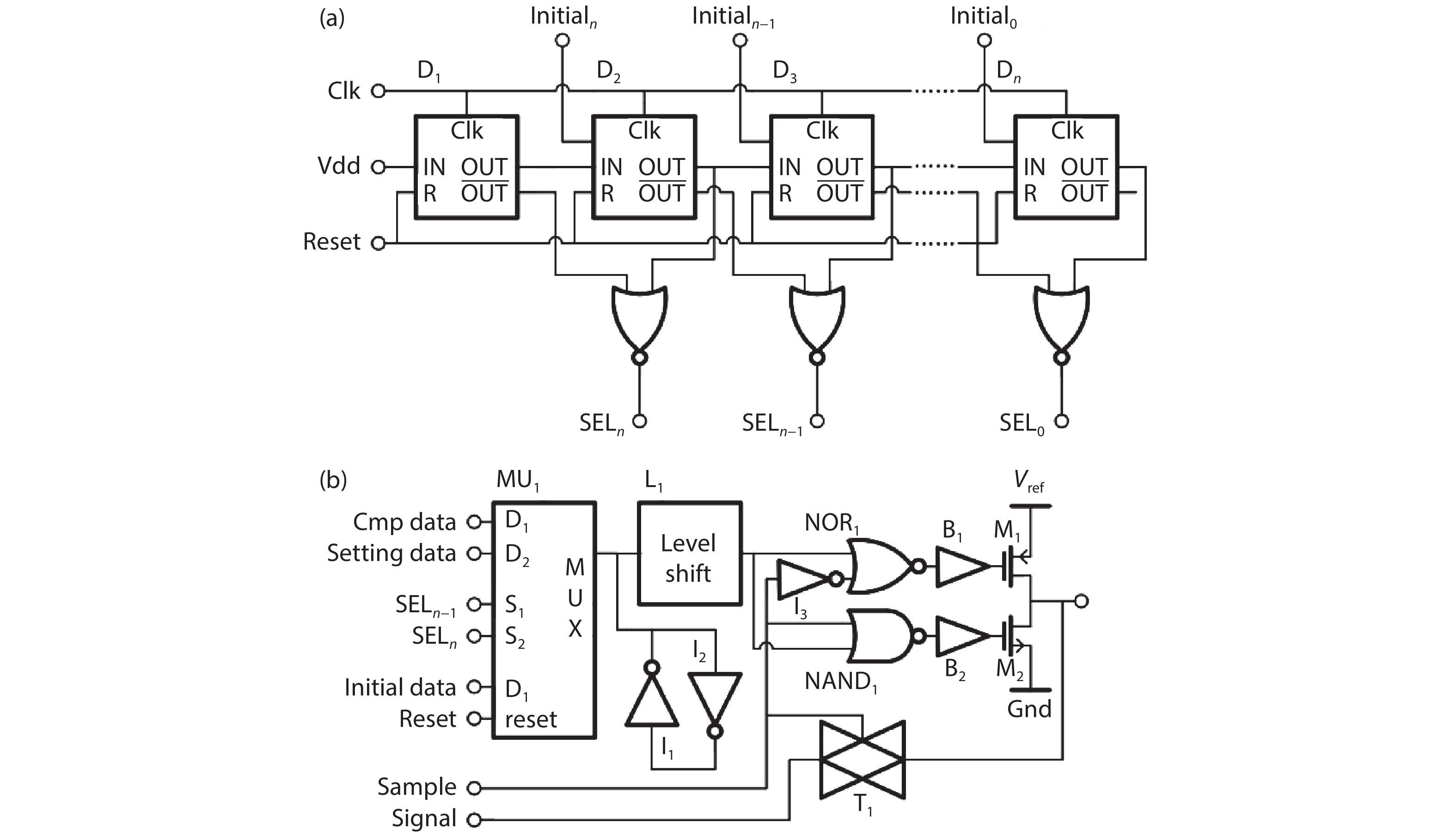
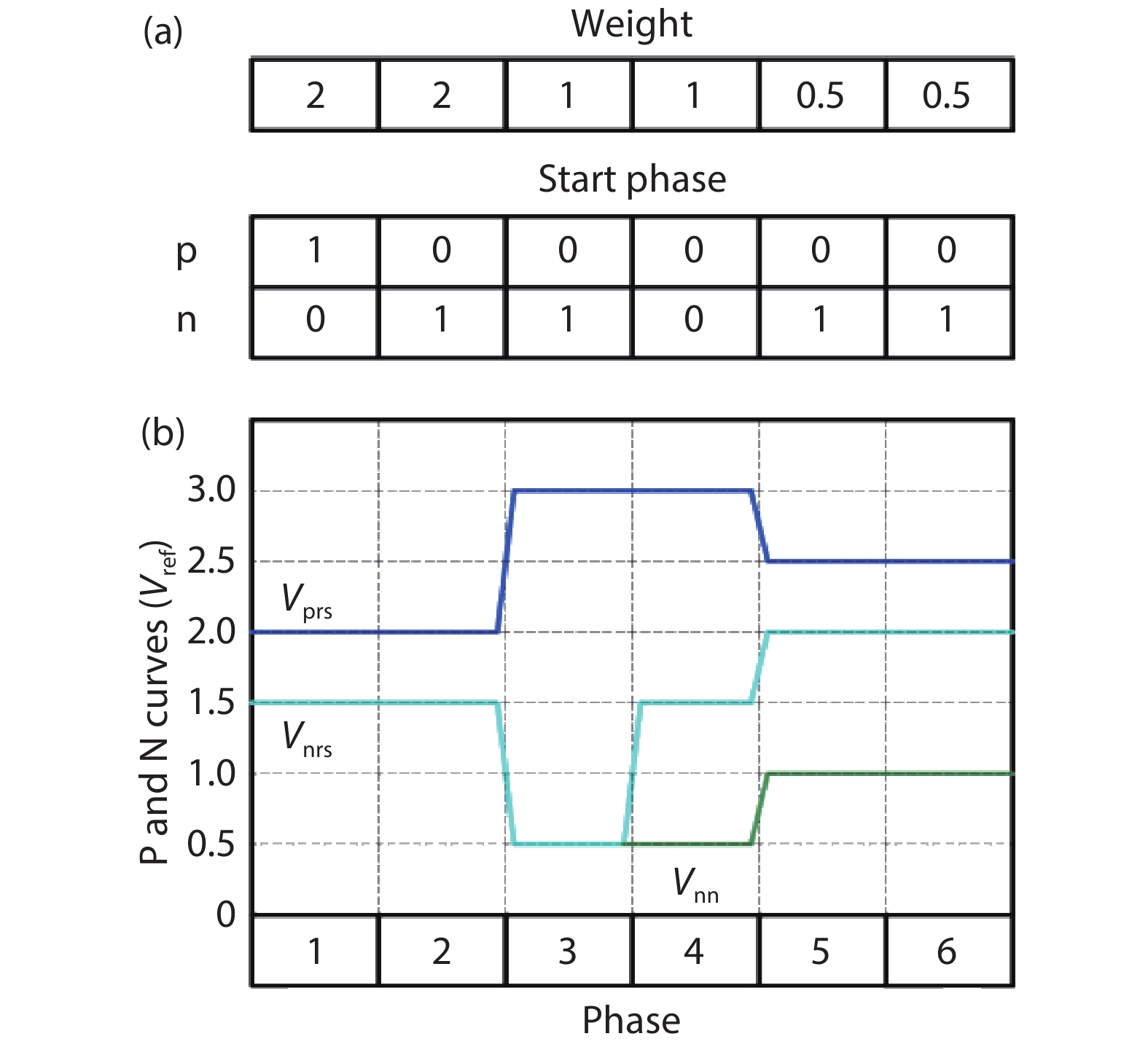
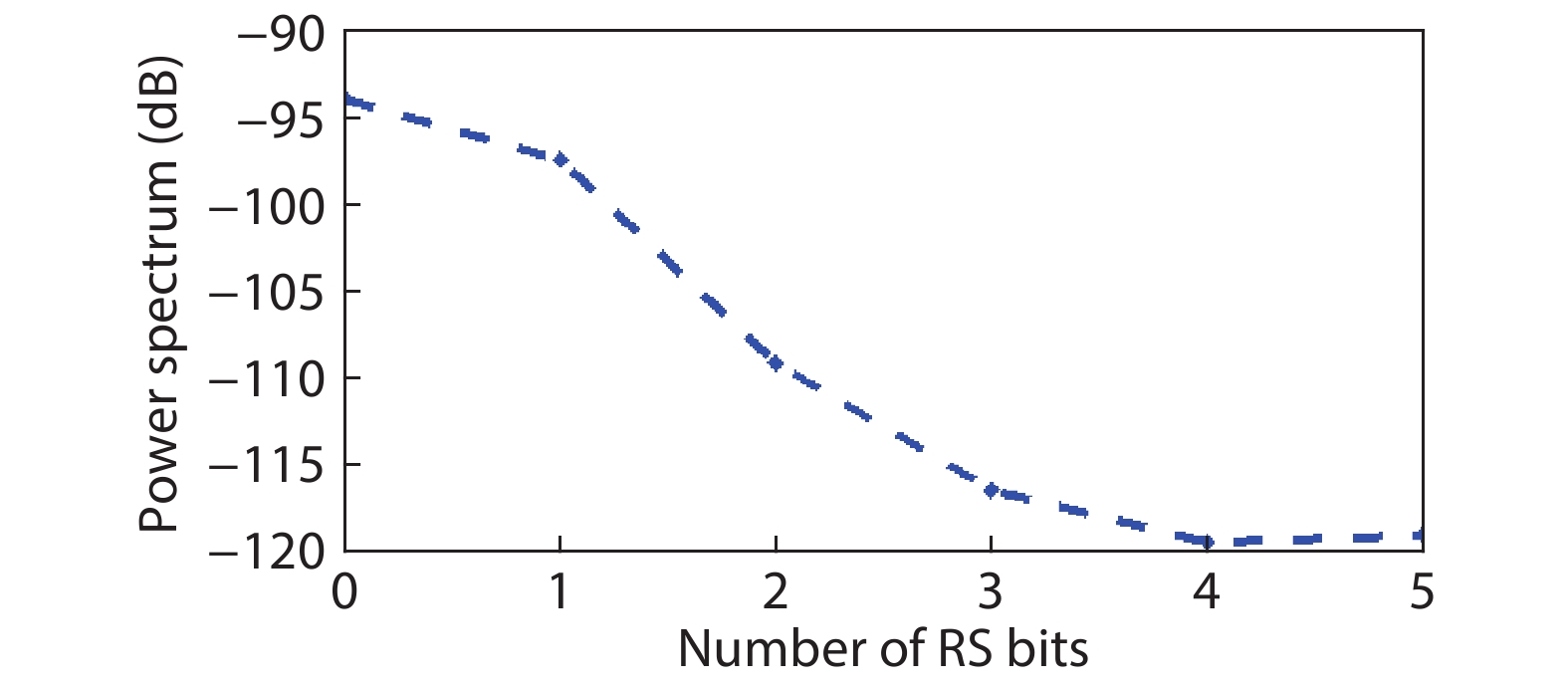
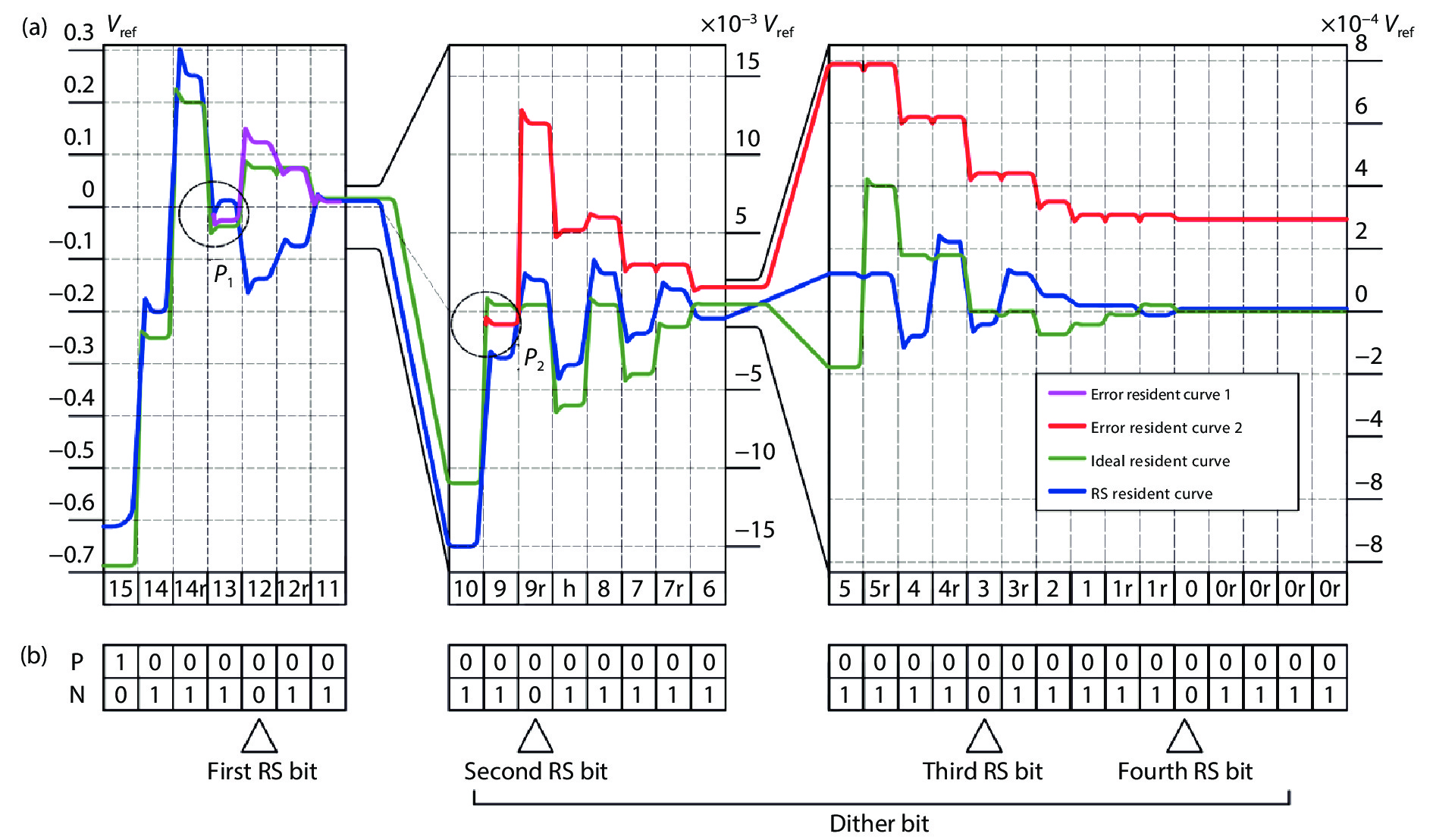
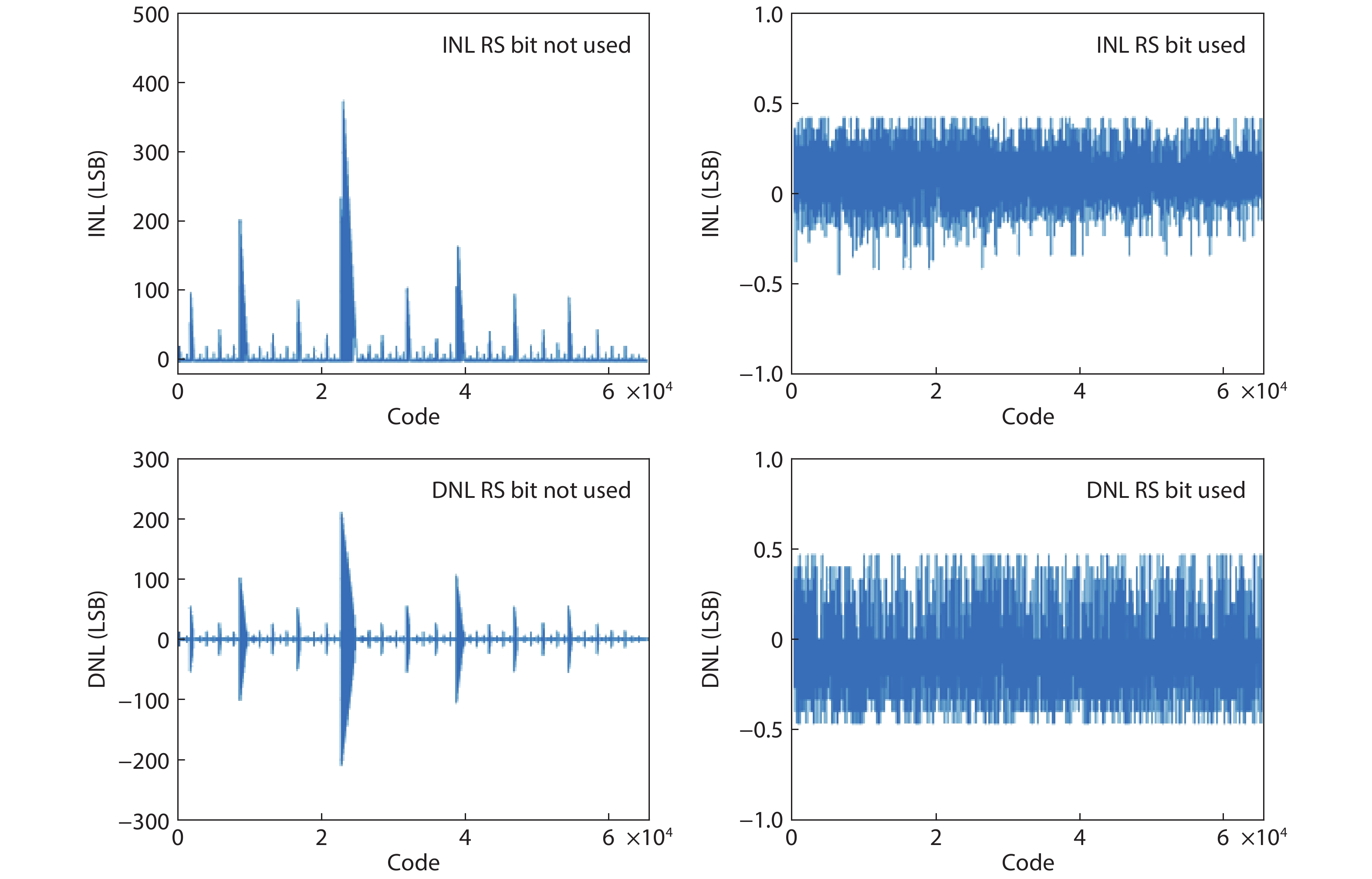
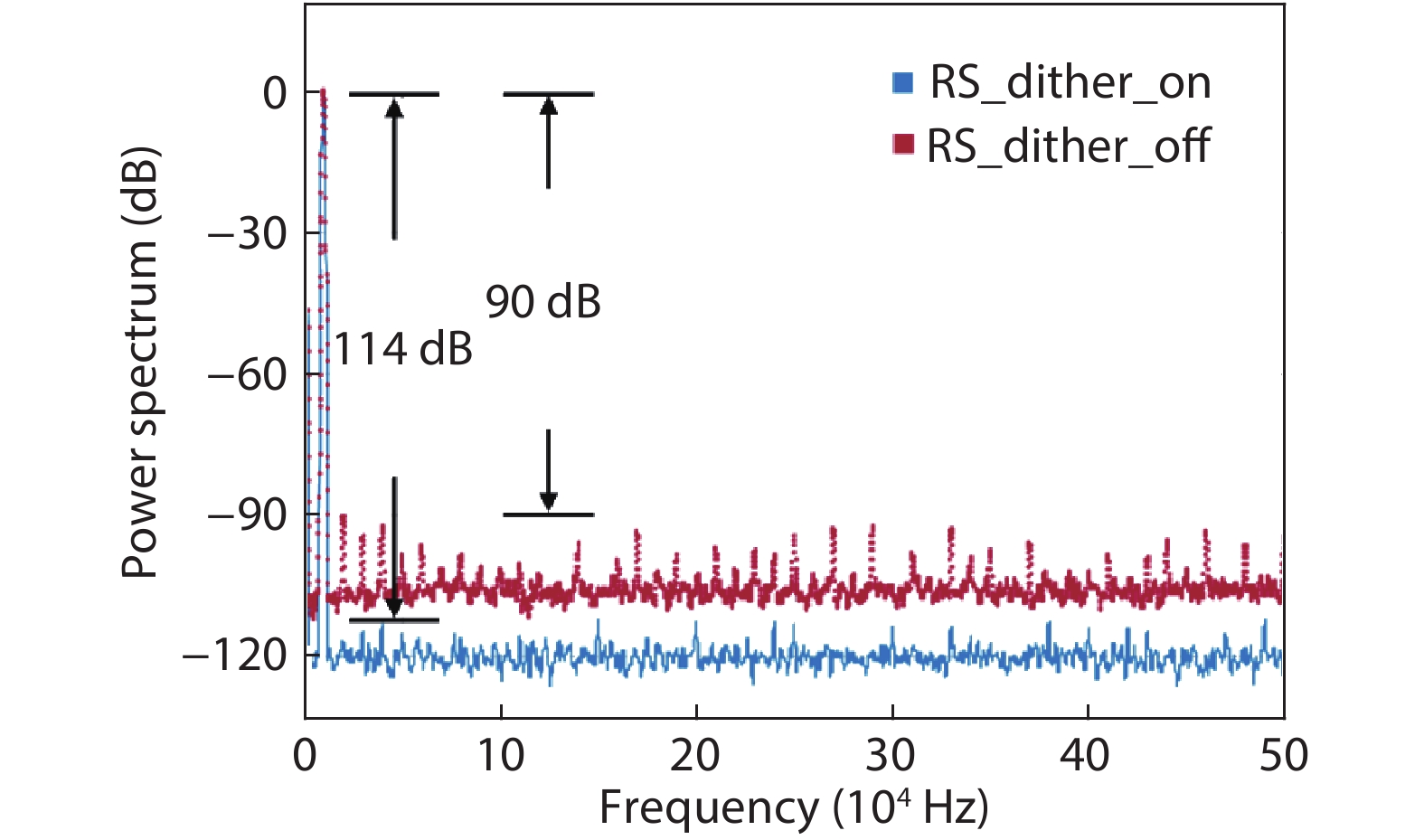
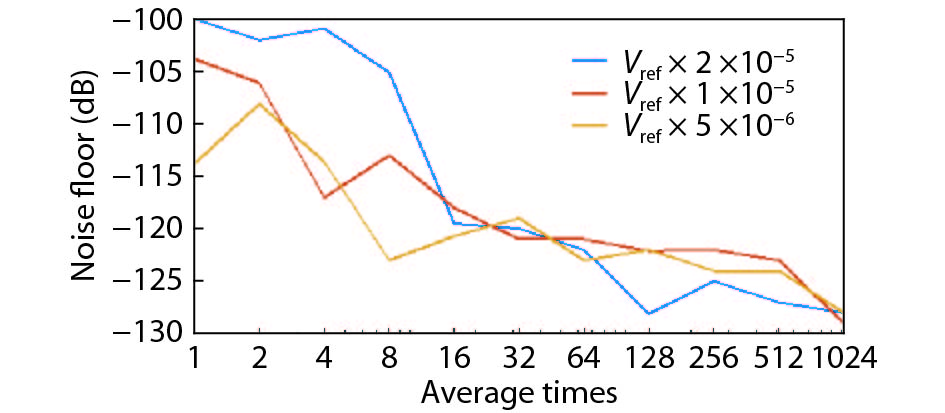
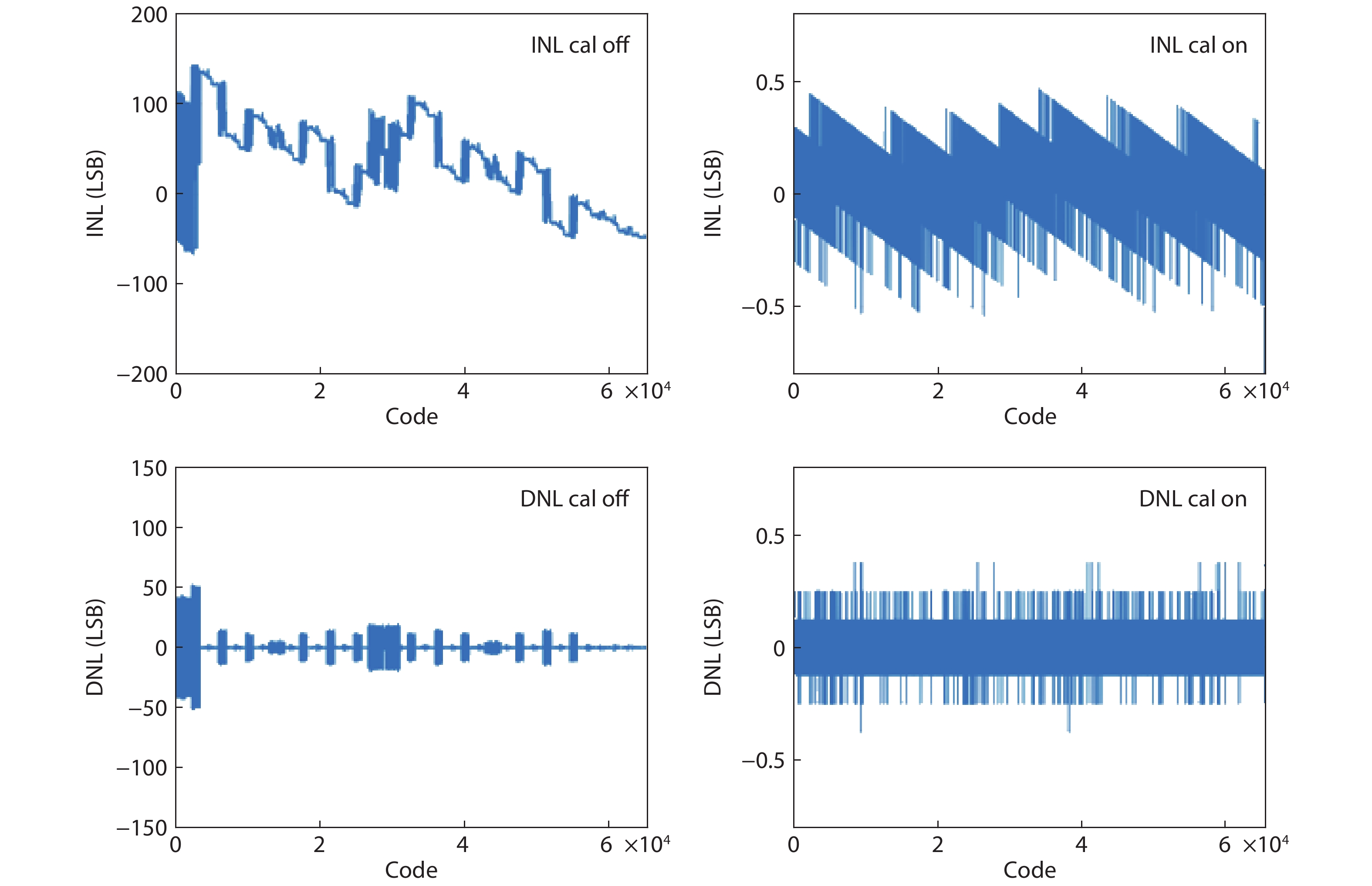
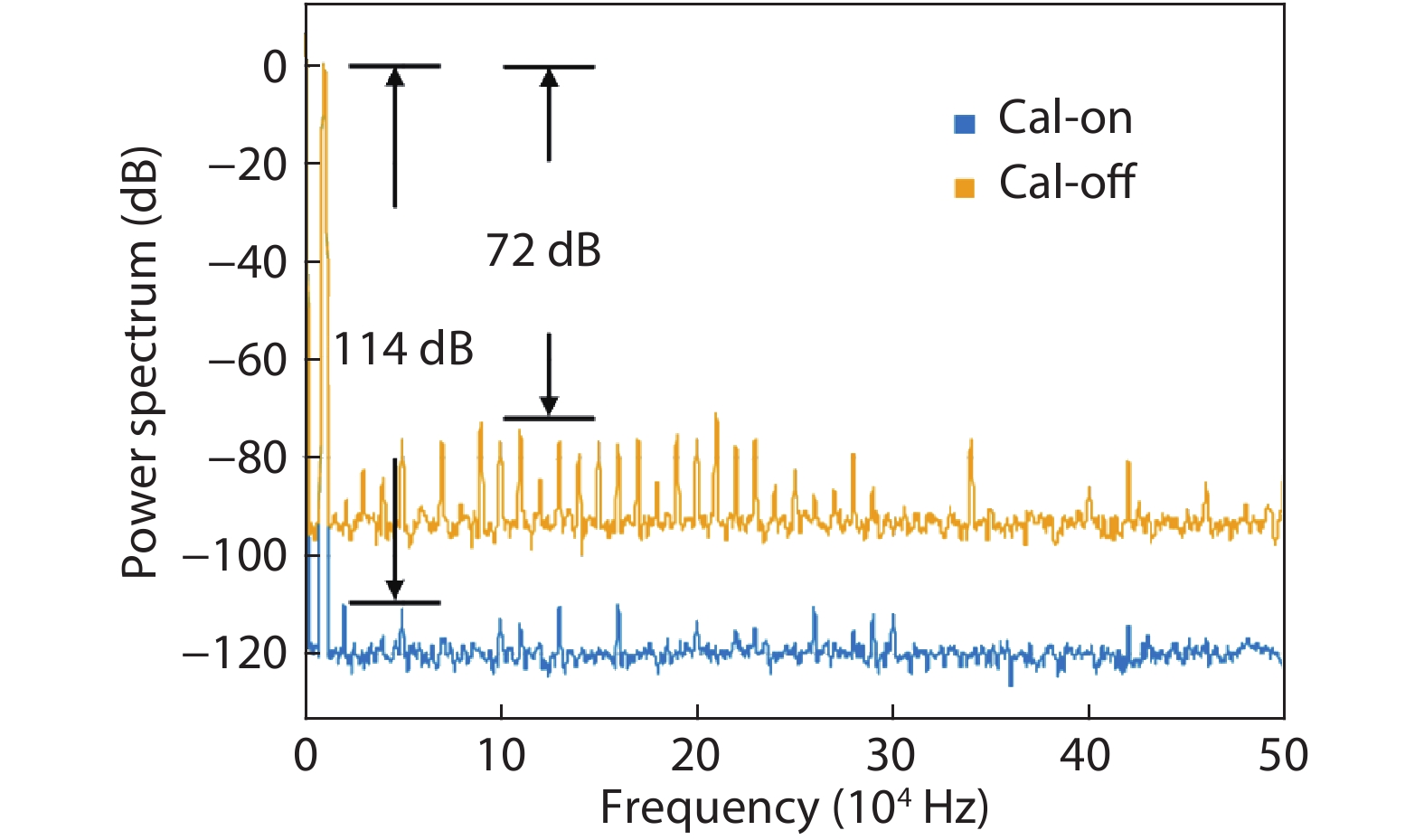
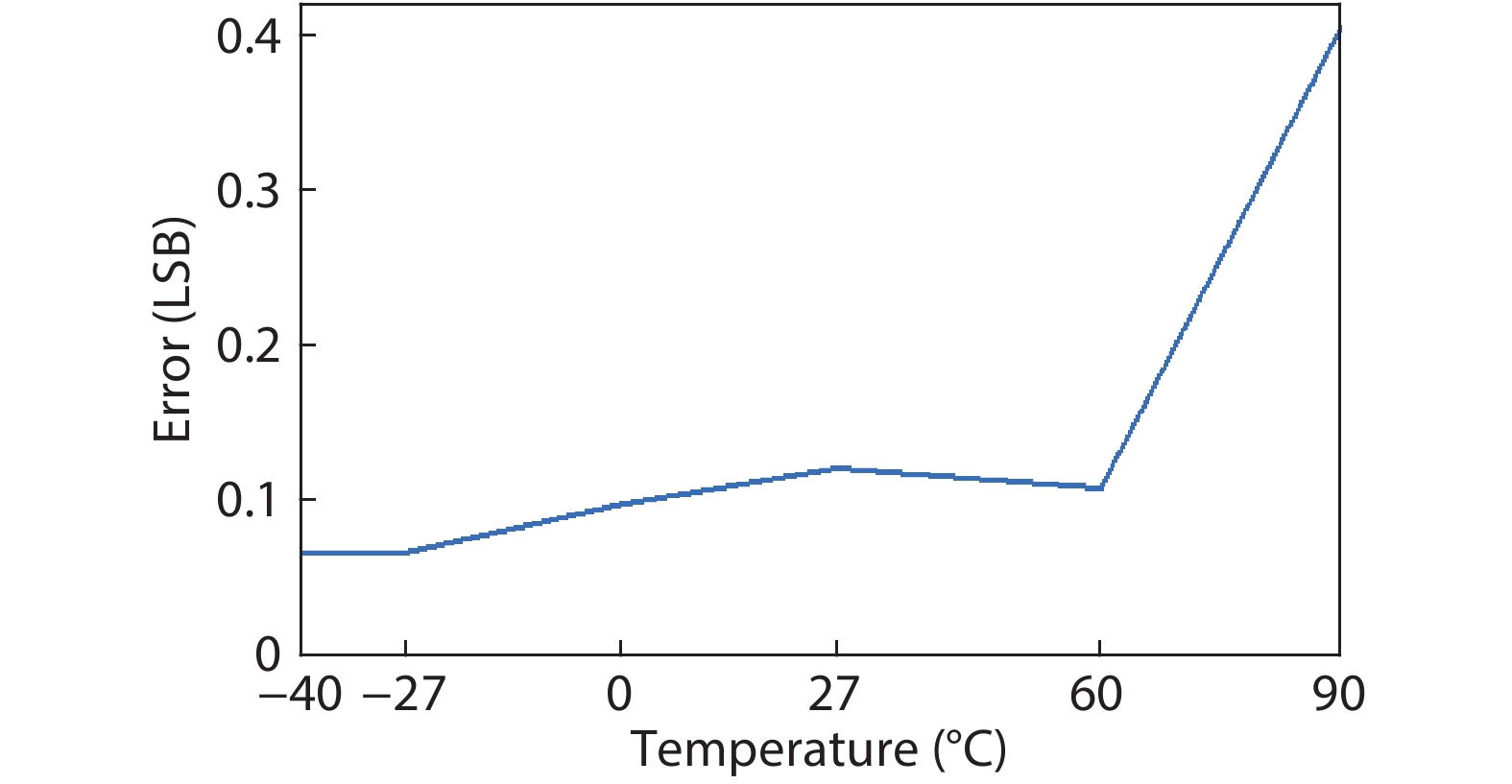
In this paper, a 16-bit 1MSPS foreground calibration successive approximation register analog-to-digital converter (SAR ADC) is developed by the CMOS 0.25 μm process. An on-chip all-digital foreground weights calibration technique integrating self-calibration weight measurement with PN port auto-balance technique is designed to improve the performance and lower the costs of the developed SAR ADC. The SAR ADC has a chip area of 2.7 × 2.4 mm2, and consumes only 100 μW at the 2.5 V supply voltage with 100 KSPS. The INL and DNL are both less than 0.5 LSB. -
References
[1] Kim W, Hong H K, Roh Y J, et al. A 0.6 V 12 b 10 MS/s low-noise asynchronous SAR-assisted time-interleaved SAR (SATI-SAR) ADC. IEEE J Solid-State Circuits, 2016, 51, 1826 doi: 10.1109/JSSC.2016.2563780[2] Shikata A, Sekimoto R, Kuroda T, et al. A 0.5 V 1.1 MS/sec 6.3 fJ/conversion-Step SAR-ADC with tri-level comparator in 40 nm CMOS. IEEE J Solid-State Circuits, 2012, 47, 1022 doi: 10.1109/JSSC.2012.2185352[3] Harpe P, Cantatore E, van Roermund A. A 10b/12b 40 kS/s SAR ADC with data-driven noise reduction achieving up to 10.1b ENOB at 2.2 fJ/conversion-step. IEEE J Solid-State Circuits, 2013, 48, 3011 doi: 10.1109/JSSC.2013.2278471[4] Nuzzo P, De Bernardinis F, Terreni P, et al. Noise analysis of regenerative comparators for reconfigurable ADC architectures. IEEE Trans Circuits Syst I, 2008, 55, 1441 doi: 10.1109/TCSI.2008.917991[5] Verbruggen B, Tsouhlarakis J, Yamamoto T, et al. A 60 dB SNDR 35 MS/s SAR ADC with comparator-noise-based stochastic residue estimation. IEEE J Solid-State Circuits, 2015, 50, 2002 doi: 10.1109/JSSC.2015.2422781[6] Zhong J Y, Zhu Y, Chan C H, et al. A 12b 180MS/s 0.068mm2 with full-calibration-integrated pipelined-SAR ADC. IEEE Trans Circuits Syst I, 2017, 64, 1684 doi: 10.1109/TCSI.2017.2679748[7] Verma N, Chandrakasan A P. An ultra low energy 12-bit rate-resolution scalable SAR ADC for wireless sensor nodes. IEEE J Solid-State Circuits, 2007, 42, 1196 doi: 10.1109/JSSC.2007.897157[8] Shen J H, Shikata A, Fernando L D, et al. A 16-bit 16-MS/s SAR ADC with on-chip calibration in 55-nm CMOS. IEEE J Solid-State Circuits, 2018, 53, 1149 doi: 10.1109/JSSC.2017.2784761[9] Chen Y, Zhu X, Tamura H, et al. Split capacitor DAC mismatch calibration in successive approximation ADC. IEICE Trans Electron, 2010, 93, 295 doi: 10.1109/CICC.2009.5280859[10] McNeill J A, Chan K Y, Coln M C W, et al. All-digital background calibration of a successive approximation ADC using the “split ADC” architecture. IEEE Trans Circuits Syst I, 2011, 58, 2355 doi: 10.1109/TCSI.2011.2123590[11] Hummerston D, Hurrell P. An 18-bit 2MS/s pipelined SAR ADC utilizing a sampling distortion cancellation circuit with –107dB THD at 100kHz. 2017 Symp VLSI Circuits, 2017, C280[12] McCreary J L, Gray P R. All-MOS charge redistribution analog-to-digital conversion techniques. I. IEEE J Solid-State Circuits, 1975, 10, 371 doi: 10.1109/JSSC.1975.1050629[13] Harpe P J, Zhou C, Bi Y, et al. A 26 W 8 bit 10 MS/s asynchronous SAR ADC for low energy radios. IEEE J Solid-State Circuits, 2011, 46, 1585 doi: 10.1109/JSSC.2011.2143870[14] Li H X, Maddox M, Coln M C W, et al. A signal-independent background-calibrating 20b 1MS/s SAR ADC with 0.3ppm INL. 2018 IEEE International Solid-State Circuits Conference, 2018[15] Liu C C, Chang S J, Huang G Y, et al. A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure. IEEE J Solid-State Circuits, 2010, 45, 731 doi: 10.1109/JSSC.2010.2042254[16] Harpe P, Zhang Y, Dolmans G, et al. A 7-to-10b 0-to-4MS/s flexible SAR ADC with 6.5-to-16fJ/conversion-step. 2012 IEEE International Solid-State Circuits Conference, 2012, 472[17] Seo M J, Roh Y J, Chang D J, et al. A reusable code-based SAR ADC design with CDAC compiler and synthesizable analog building blocks. IEEE Trans Circuits Syst II, 2018, 65, 1904 doi: 10.1109/TCSII.2018.2822811[18] Harpe P, Cantatore E, van Roermund A. An oversampled 12/14b SAR ADC with noise reduction and linearity enhancements achieving up to 79.1dB SNDR. 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), 2014, 194[19] Miki T, Morie T, Matsukawa K, et al. A 4.2 mW 50 MS/s 13 bit CMOS SAR ADC With SNR and SFDR enhancement techniques. IEEE J Solid-State Circuits, 2015, 50, 1372 doi: 10.1109/JSSC.2015.2417803[20] Hurrell C P, Lyden C, Laing D, et al. An 18 b 12.5 MS/s ADC with 93 dB SNR. IEEE J Solid-State Circuits, 2010, 45, 2647 doi: 10.1109/JSSC.2010.2075310[21] Wagdy M F, Goff M. Linearizing average transfer characteristics of ideal ADC's via analog and digital dither. IEEE Trans Instrum Meas, 1994, 43, 146 doi: 10.1109/19.293411[22] Lee C C, Lu C Y, Narayanaswamy R, et al. A 12b 70MS/s SAR ADC with digital startup calibration in 14nm CMOS. 2015 Symposium on VLSI Circuits (VLSI Circuits), 2015, C62[23] Shen J H, Shikata A, Fernando L, et al. A 16-bit 16MS/s SAR ADC with on-chip calibration in 55nm CMOS. 2017 Symposium on VLSI Circuits Digest of Technical Papers, 2017[24] Maddox M, Chen B Z, Coln M, et al. A 16 bit linear passive-charge-sharing SAR ADC in 55nm CMOS. 2016 IEEE Asian Solid-State Circuits Conf (A-SSCC), 2016, 153 -
Proportional views





 DownLoad:
DownLoad: