| Citation: |
Jing Teng, Nan Liu, Yongqing Li. Mn-doped topological insulators: a review[J]. Journal of Semiconductors, 2019, 40(8): 081507. doi: 10.1088/1674-4926/40/8/081507
****
J Teng, N Liu, Y Q Li, Mn-doped topological insulators: a review[J]. J. Semicond., 2019, 40(8): 081507. doi: 10.1088/1674-4926/40/8/081507.
|
-
Abstract
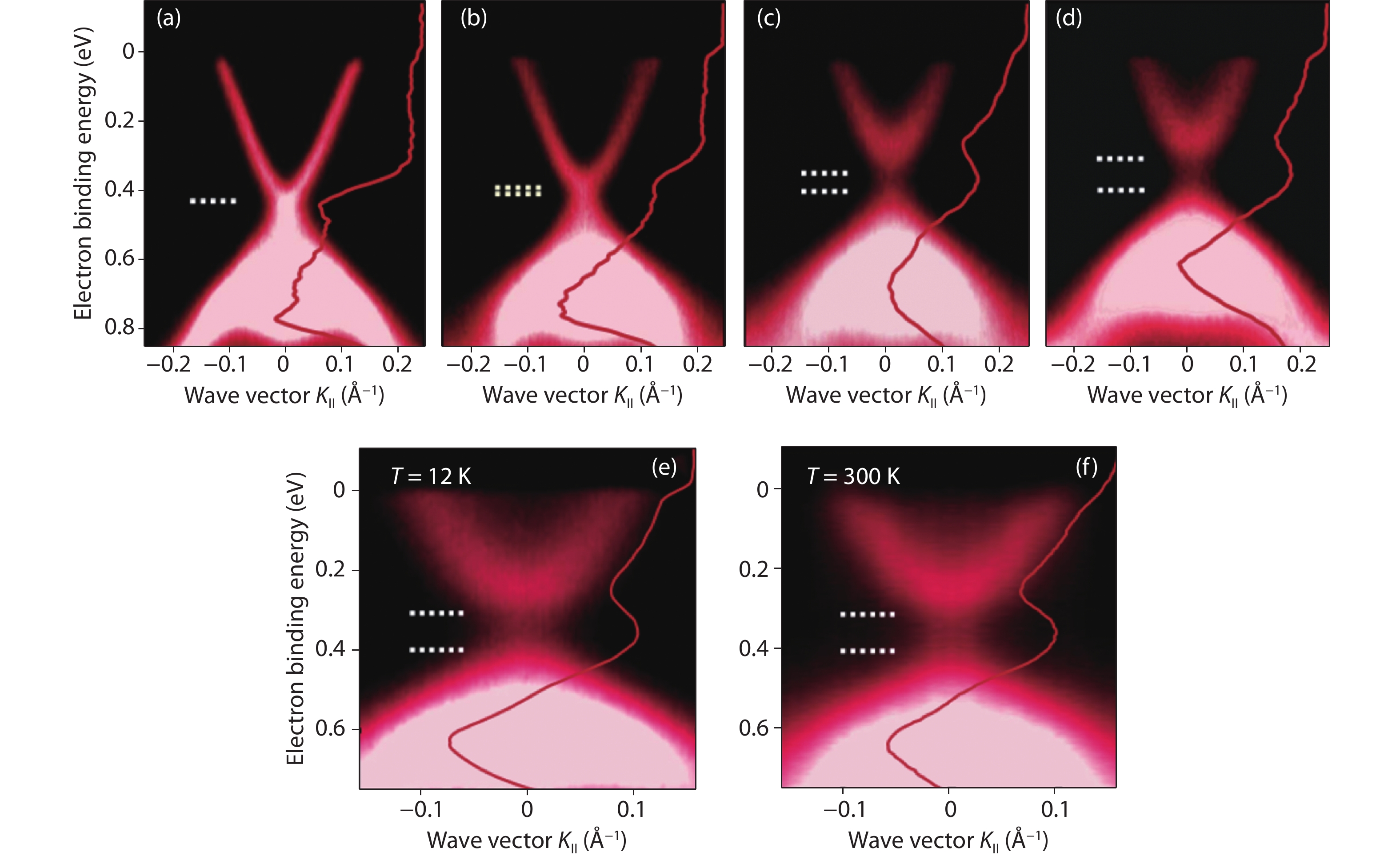
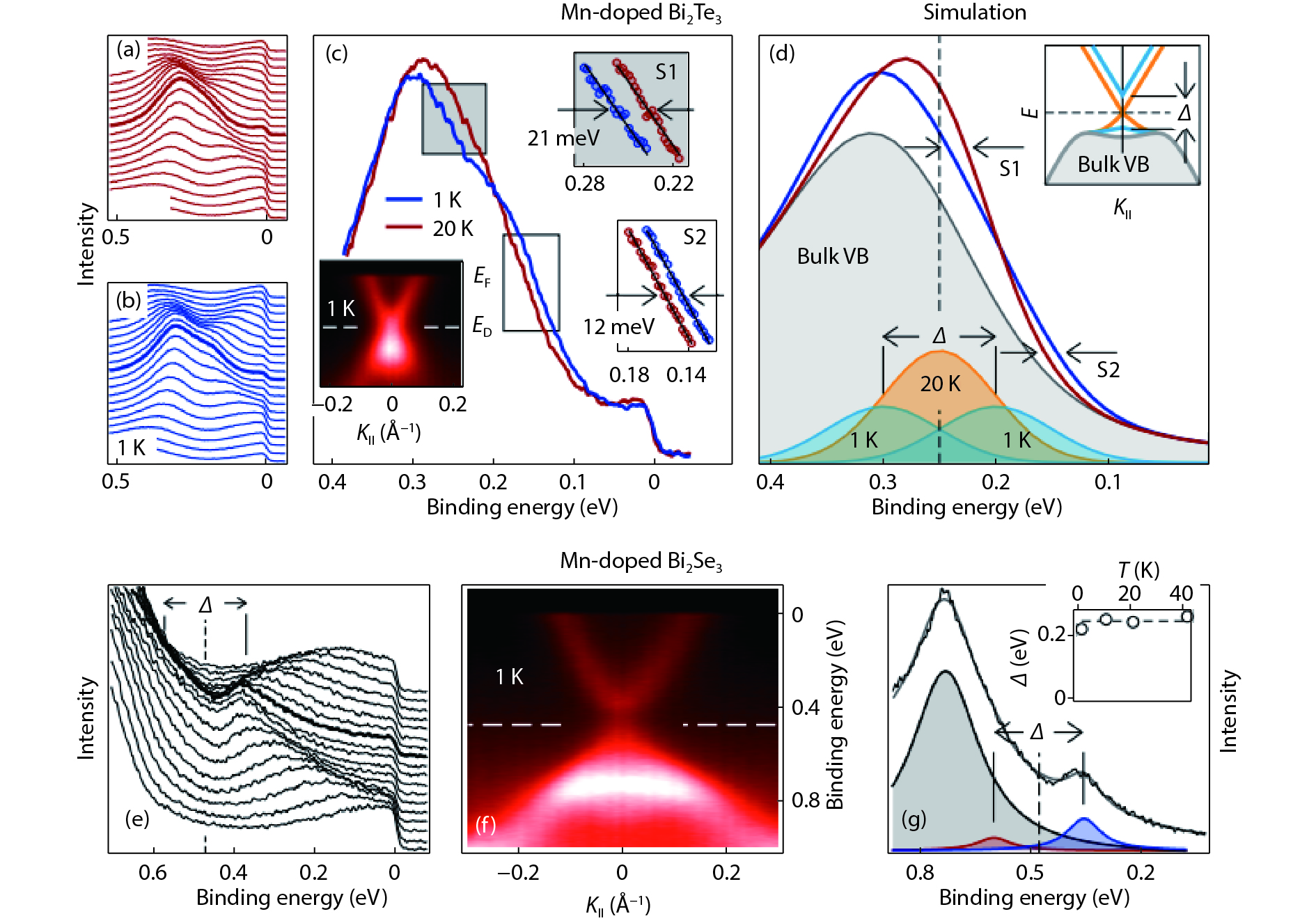
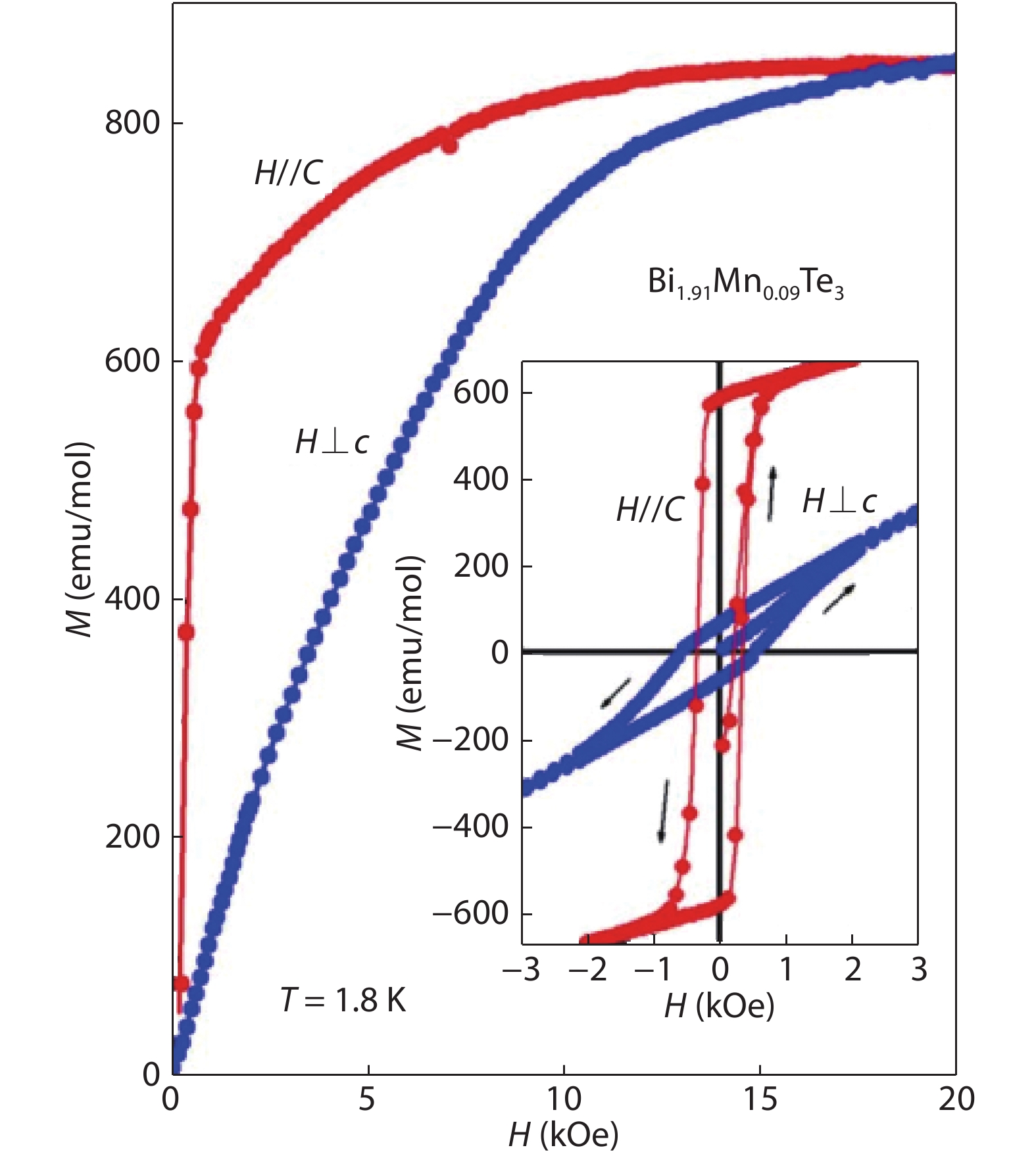
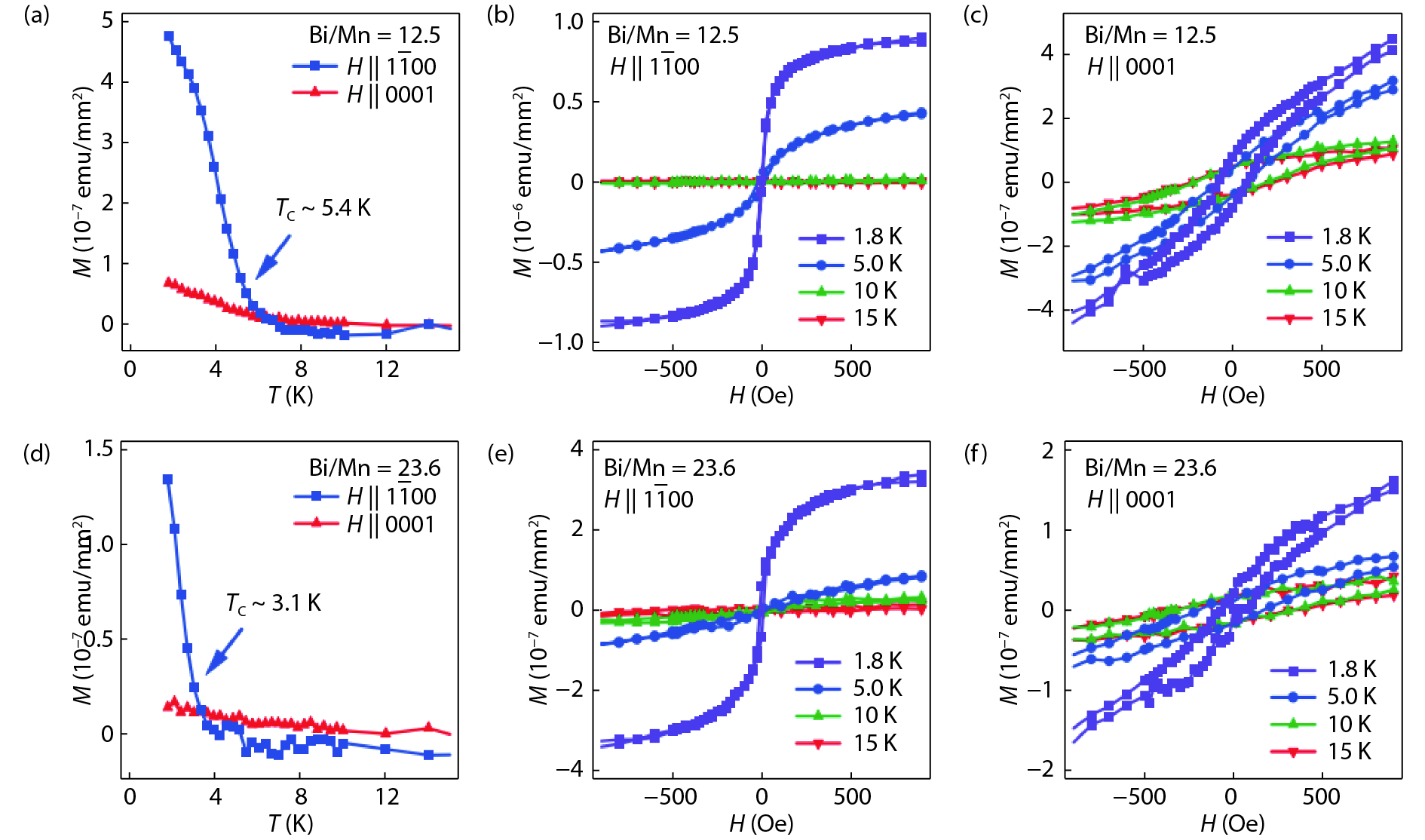
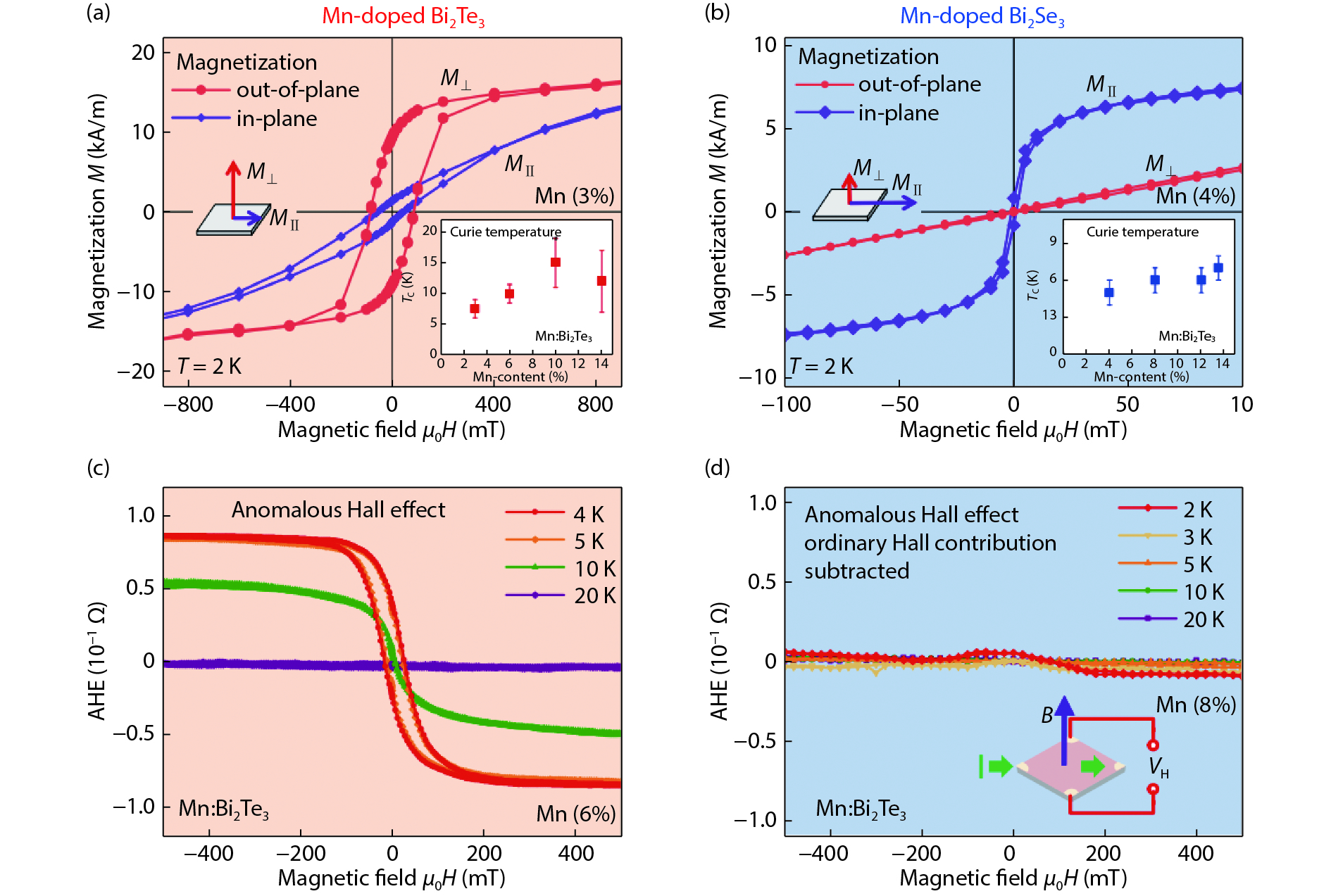
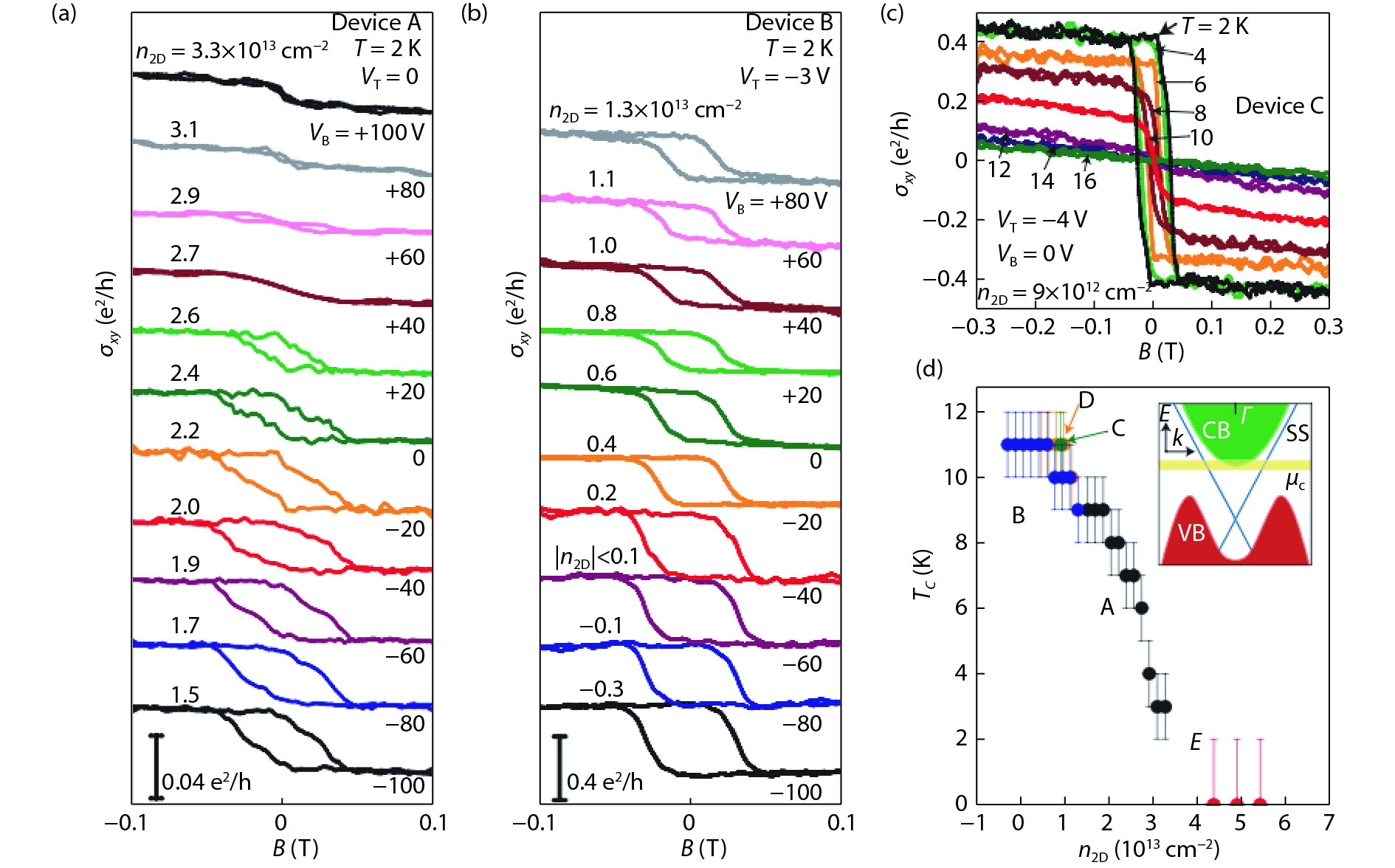
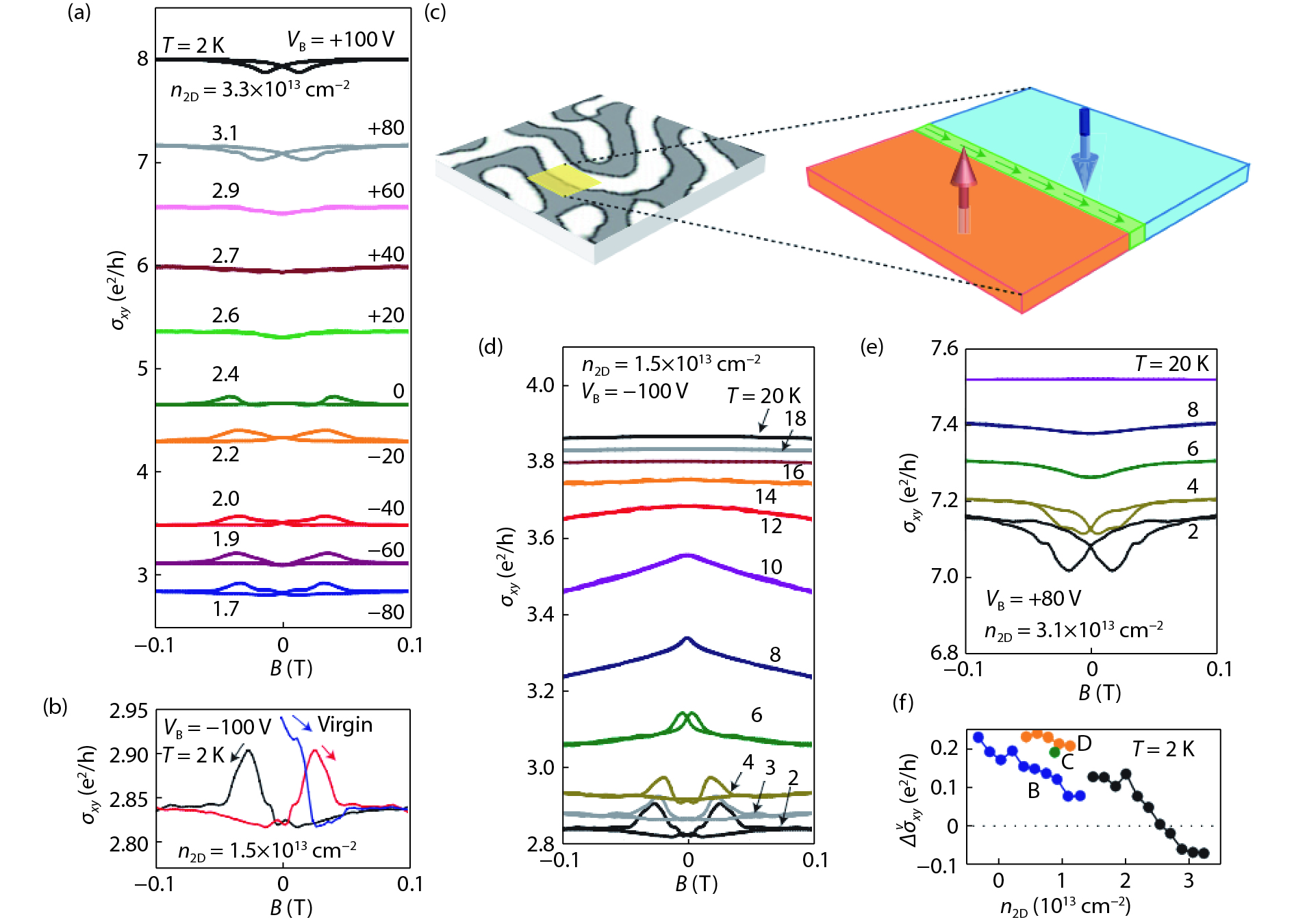
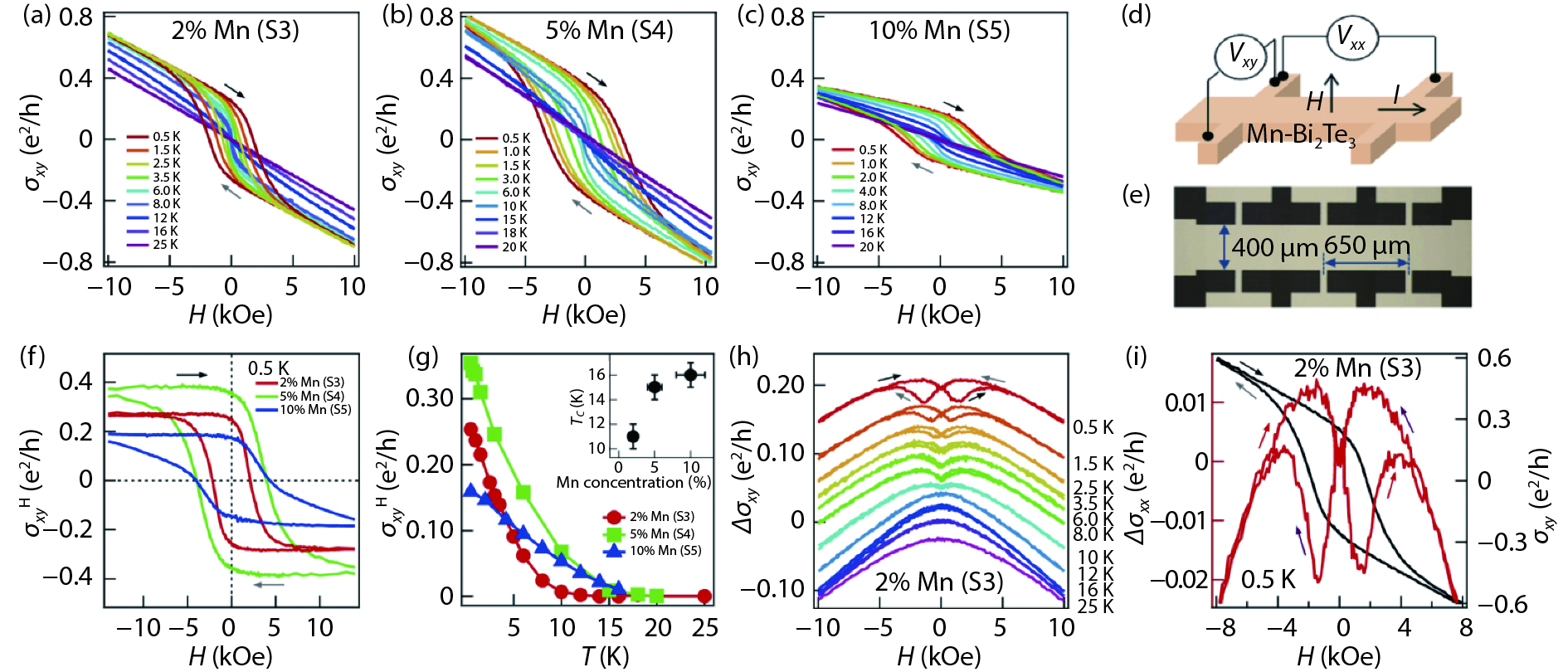
Topological insulators (TIs) host robust edge or surface states protected by time-reversal symmetry (TRS), which makes them prime candidates for applications in spintronic devices. A promising avenue of research for the development of functional TI devices has involved doping of three-dimensional (3D) TI thin film and bulk materials with magnetic elements. This approach aims to break the TRS and open a surface band gap near the Dirac point. Utilizing this gapped surface state allows for a wide range of novel physical effects to be observed, paving a way for applications in spintronics and quantum computation. This review focuses on the research of 3D TIs doped with manganese (Mn). We summarize major progress in the study of Mn doped chalcogenide TIs, including Bi2Se3, Bi2Te3, and Bi2(Te,Se)3. The transport properties, in particular the anomalous Hall effect, of the Mn-doped Bi2Se3 are discussed in detail. Finally, we conclude with future prospects and challenges in further studies of Mn doped TIs. -
References
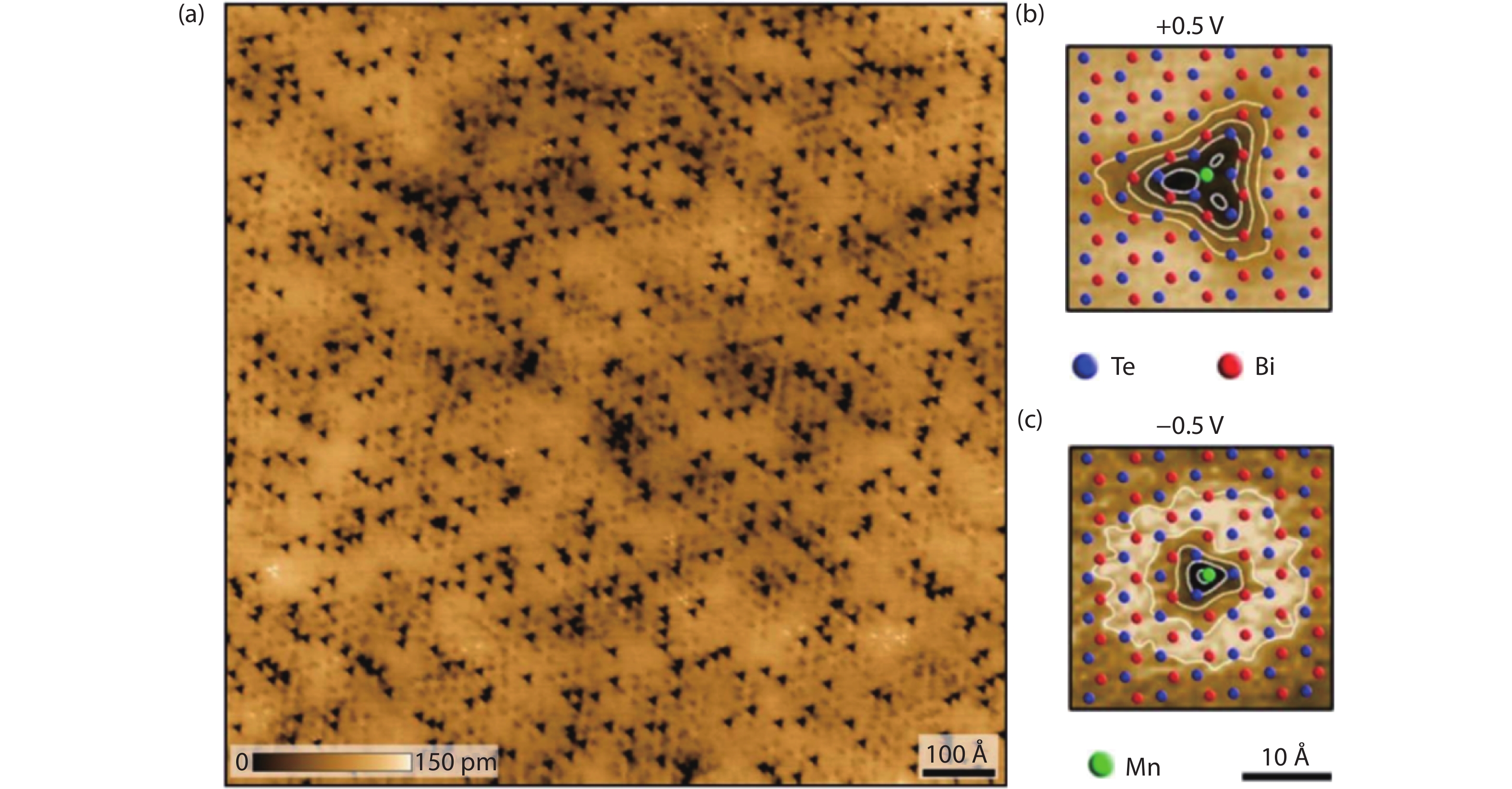
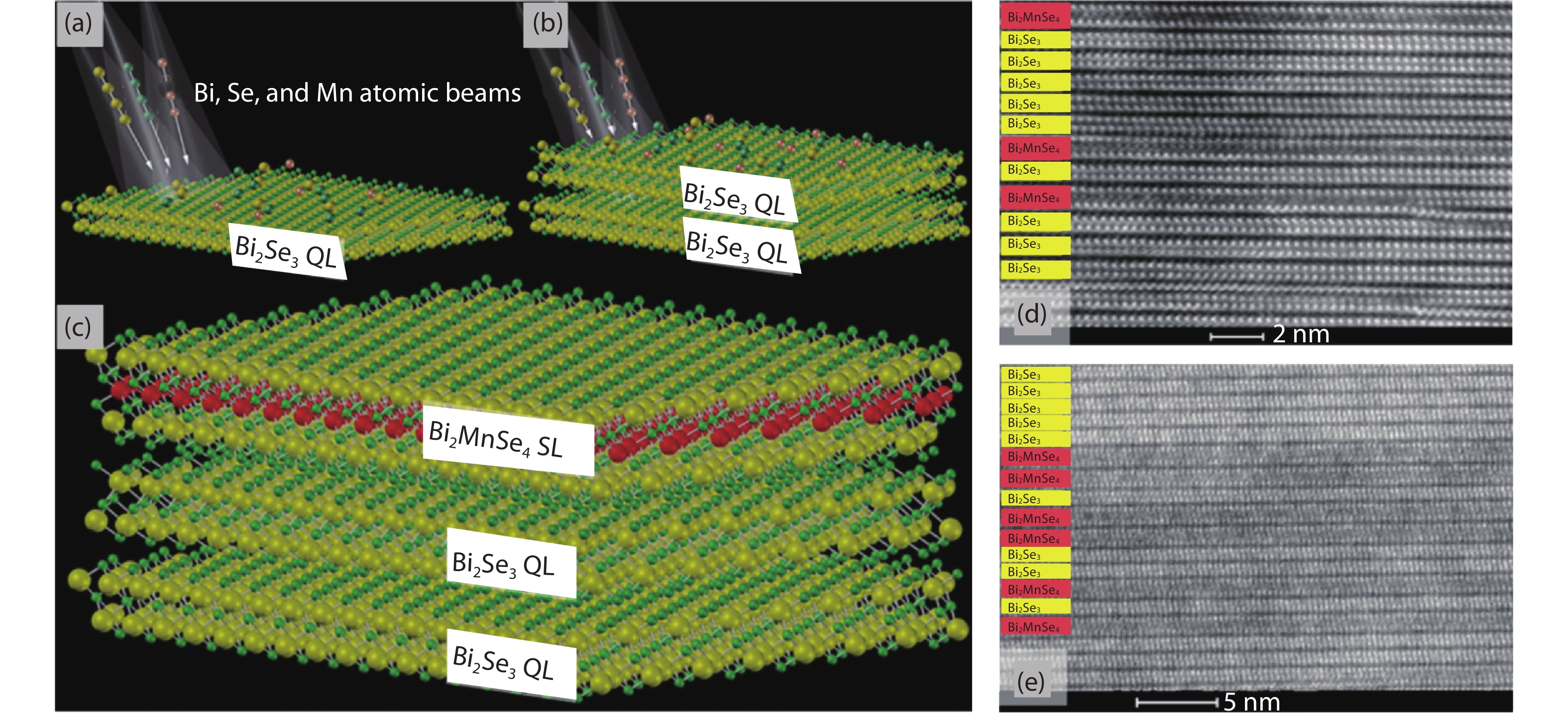
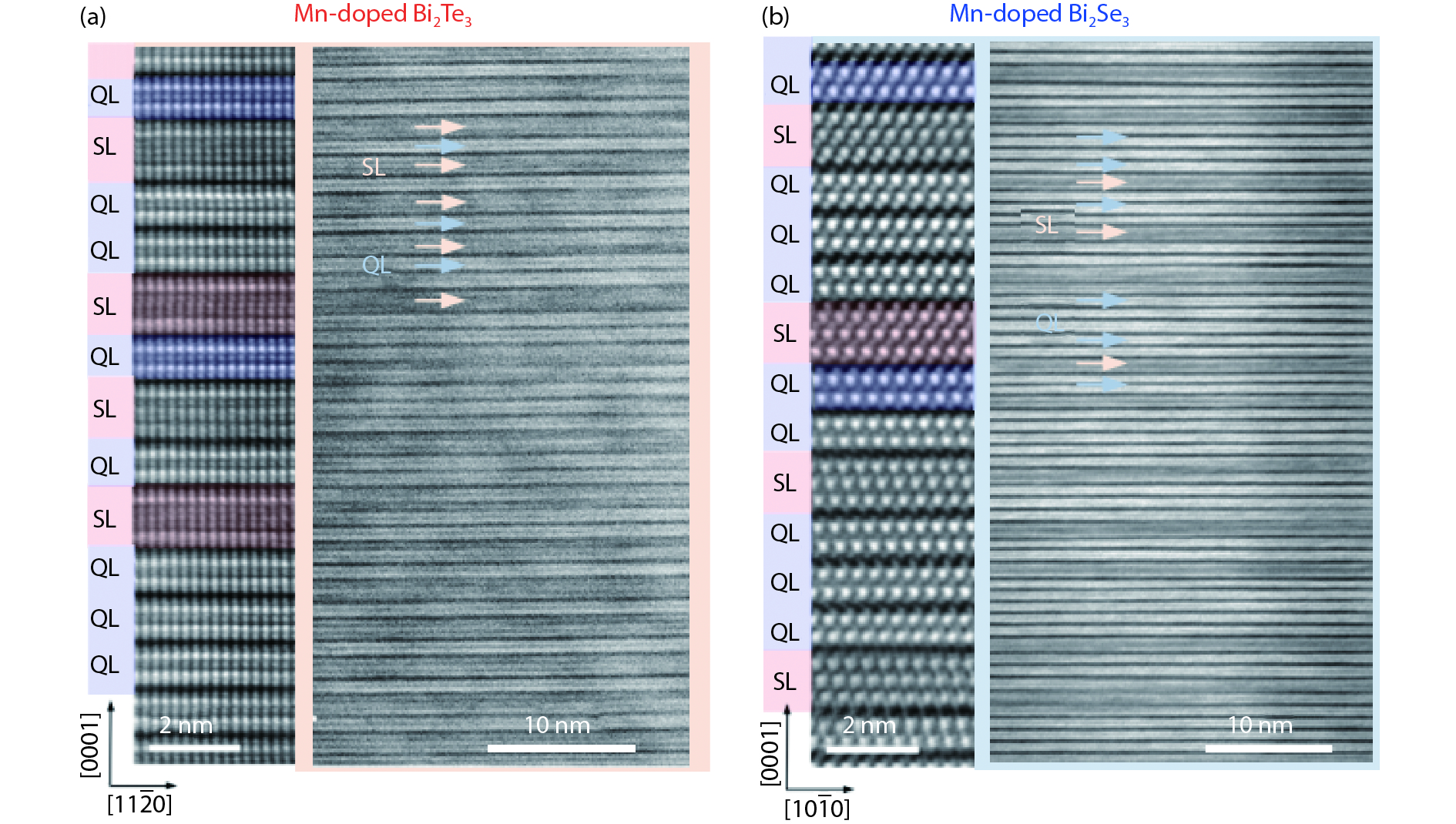
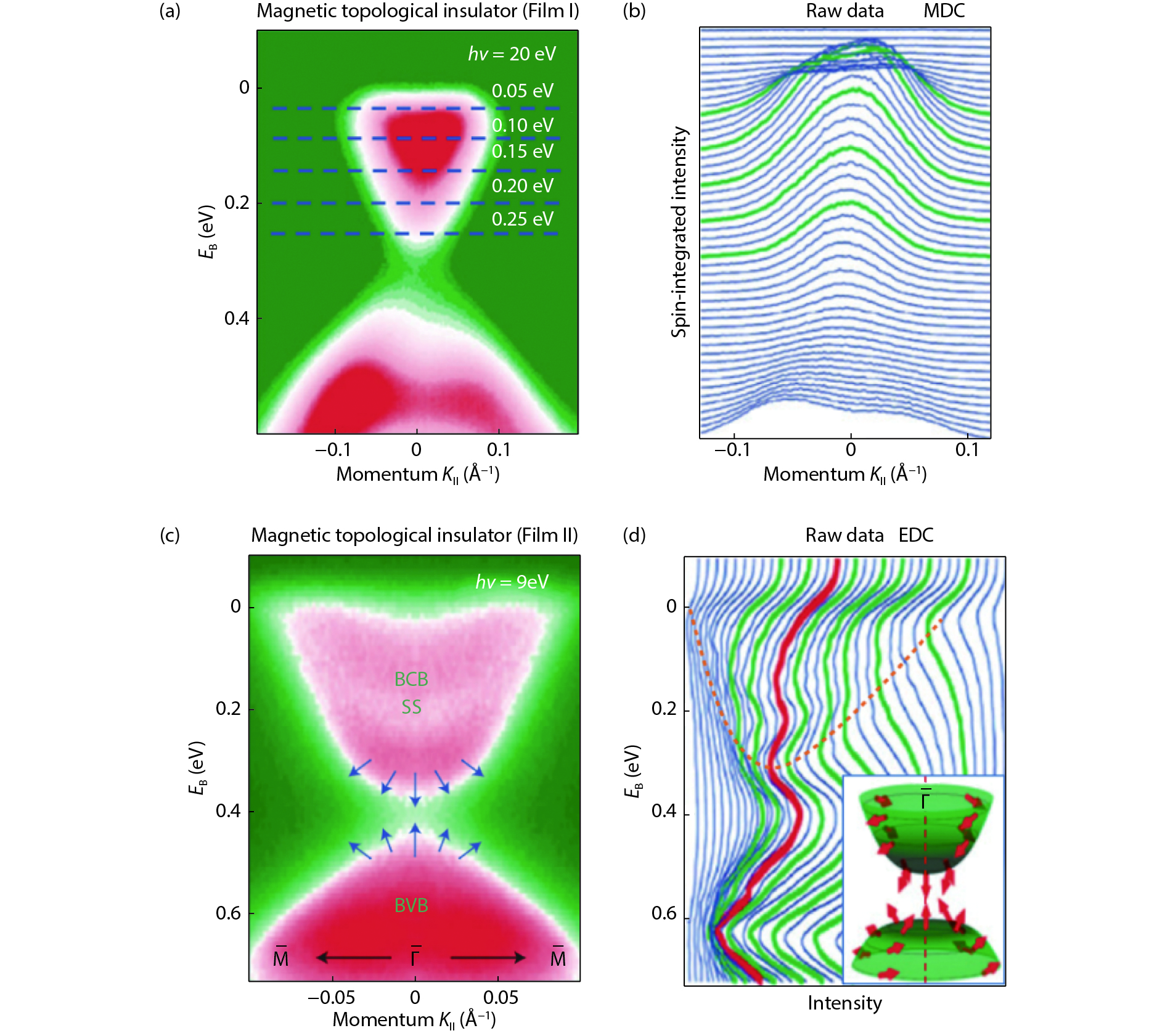
[1] Kane C L, Mele E J. Z2 topological order and the quantum spin Hall effect. Phys Rev Lett, 2005, 95, 146802 doi: 10.1103/PhysRevLett.95.146802[2] Kane C L, Mele E J. Quantum spin Hall effect in graphene. Phys Rev Lett, 2005, 95, 226801 doi: 10.1103/PhysRevLett.95.226801[3] Zhang Y, Tan Y W, Stormer H L, et al. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature, 2005, 438, 201 doi: 10.1038/nature04235[4] Bernevig B A, Zhang S C. Quantum spin Hall effect. Phys Rev Lett, 2006, 96, 106802 doi: 10.1103/PhysRevLett.96.106802[5] Prange R E, Girvin S M. The quantum Hall effect. New York: Springer-Verlag, 1990[6] Klitzing K V, Dorda G, Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys Rev Lett, 1980, 45, 494 doi: 10.1103/PhysRevLett.45.494[7] Thouless D J, Kohmoto M, Nightingale M P, et al. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett, 1982, 49, 405 doi: 10.1103/PhysRevLett.49.405[8] Simon B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys Rev Lett, 1983, 51, 2167 doi: 10.1103/PhysRevLett.51.2167[9] Bernevig B A, Hughes T L, Zhang S C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science, 2006, 314, 1757 doi: 10.1126/science.1133734[10] Koenig M, Wiedmann S, Bruene C, et al. Quantum spin Hall insulator state in HgTe quantum wells. Science, 2007, 318, 766 doi: 10.1126/science.1148047[11] Qi X L, Zhang S C. Topological insulators and superconductors. Rev Mov Phys, 2011, 83, 1057 doi: 10.1103/revmodphys.83.1057[12] Ando Y. Topological insulator materials. J Phys Soc Jpn, 2013, 82, 102001 doi: 10.7566/JPSJ.82.102001[13] Fu L, Kane C L, Mele E J. Topological insulators in three dimensions. Phys Rev Lett, 2007, 98, 106803 doi: 10.1103/physrevlett.98.106803[14] Hsieh D, Qian D, Wray L, et al. A topological Dirac insulator in a quantum spin Hall phase. Nature, 2008, 452, 970 doi: 10.1038/nature06843[15] Xia Y, Qian D, Hsieh D, et al. Observation of a large-gap topological insulator class with a single Dirac cone on the surface. Nat Phys, 2009, 5, 398 doi: 10.1038/nphys1274[16] Chen Y L, Analytis J G, Chu J H, et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science, 2009, 325, 178 doi: 10.1126/science.1173034[17] Zhang H, Liu C X, Qi X L, et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat Phys, 2009, 5, 438 doi: 10.1038/nphys1270[18] Chen J, Qin H J, Yang F, et al. Gate-voltage control of chemical potential and weak antilocalization in Bi2Se3. Phys Rev Lett, 2010, 105, 176602 doi: 10.1103/PhysRevLett.105.176602[19] Qu D X, Hor Y S, Xiong J, et al. Quantum oscillations and Hall anomaly of surface states in the topological insulator Bi2Te3. Science, 2010, 329, 821 doi: 10.1126/science.1189792[20] Analytis J G, Chu J H, Chen Y, et al. Bulk Fermi surface coexistence with Dirac surface state in Bi2Se3: A comparison of photoemission and Shubnikov–de Haas measurements. Phys Rev B, 2010, 81, 205407 doi: 10.1103/PhysRevB.81.205407[21] Yu R, Zhang W, Zhang H J, et al. Quantized anomalous Hall effect in magnetic topological insulators. Science, 2010, 329, 61 doi: 10.1126/science.1187485[22] Chang C Z, Zhang J, Feng X, et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science, 2013, 340, 167 doi: 10.1126/science.1234414[23] Mellnik A R, Lee J S, Richardella A, et al. Spin-transfer torque generated by a topological insulator. Nature, 2014, 511, 449 doi: 10.1038/nature13534[24] Qi X L, Hughes T L, Zhang S C. Topological field theory of time-reversal invariant insulators. Phys Rev B, 2008, 78, 195424 doi: 10.1103/physrevb.78.195424[25] Essin A M, Moore J E, Vanderbilt D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys Rev Lett, 2009, 102, 146805 doi: 10.1103/PhysRevLett.102.146805[26] Tse W K, MacDonald A H. Giant magneto-optical Kerr effect and universal Faraday effect in thin-film topological insulators. Phys Rev Lett, 2010, 105, 057401 doi: 10.1103/PhysRevLett.105.057401[27] Li R, Wang J, Qi X L, et al. Dynamical axion field in topological magnetic insulators. Nat Phys, 2010, 6, 284 doi: 10.1038/nphys1534[28] Fu L, Kane C L. Superconducting proximity effect and Majorana Fermions at the surface of a topological insulator. Phys Rev Lett, 2008, 100, 096407 doi: 10.1103/physrevlett.100.096407[29] Qi X L, Li R, Zang J, et al. Inducing a magnetic monopole with topological surface states. Science, 2009, 323, 1184 doi: 10.1126/science.1167747[30] Hasan M Z, Kane C L. Colloquium: topological insulators. Rev Mod Phys, 2010, 82, 3045 doi: 10.1103/revmodphys.82.3045[31] Lu H Z, Shi J, Shen S Q. Competition between weak localization and antilocalization in topological surface states. Phys Rev Lett, 2011, 107, 076801 doi: 10.1103/PhysRevLett.107.076801[32] Checkelsky J G, Yoshimi R, Tsukazaki A, et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat Phys, 2014, 10, 731 doi: 10.1038/nphys3053[33] Kou X, Guo S T, Fan Y, et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys Rev Lett, 2014, 113, 137201 doi: http://dx.doi.org/10.1103/PhysRevLett.113.199901[34] Bestwick A J, Fox E J, Kou X, et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys Rev Lett, 2015, 114, 187201 doi: 10.1103/PhysRevLett.114.187201[35] Chang C Z, Zhao W, Kim D Y, et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat Mater, 2015, 14, 473 doi: 10.1038/nmat4204[36] Chen Y L, Chu J H, Analytis J G, et a. Massive Dirac Fermion on the surface of a magnetically doped topological insulator. Science, 2010, 329, 659 doi: 10.1126/science.1189924[37] Xu S Y, Neupane M, Liu C, et al. Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator. Nat Phys, 2012, 8, 616 doi: 10.1038/nphys2351[38] Rienks E D L, Wimmer S, Mandal P S, et al. Large magnetic gap at the Dirac point in a Mn-induced Bi2Te3 heterostructure. arXiv: 1810.06238[39] Zhang J M, Ming W, Huang Z, et al. Stability, electronic, and magnetic properties of the magnetically doped topological insulators Bi2Se3, Bi2Te3 and Sb2Te3. Phys Rev B, 2013, 88, 235131 doi: 10.1103/PhysRevB.88.235131[40] Abdalla L B, Seixas L, Schmidt T M, et al. Topological insulator Bi2Se3(111) surface doped with transition metals: An ab initio investigation. Phys Rev B, 2013, 88, 045312 doi: 10.1103/PhysRevB.88.045312[41] Růžička J, Caha O, Hol V, et al. Structural and electronic properties of manganese doped Bi2Te3 epitaxial layers. New J Phys, 2015, 17, 013028 doi: 10.1088/1367-2630/17/1/013028[42] Lee J S, Richardella A, Rench D W, et al. Ferromagnetism and spin-dependent transport in n-type Mn-doped bismuth telluride thin films. Phys Rev B, 2014, 89, 174425 doi: 10.1103/PhysRevB.89.174425[43] Figueroa A I, van der Laan G, Collins-McIntyre L J, et al. Local structure and bonding of transition metal dopants in Bi2Se3 topological insulator thin films. J Phys Chem C, 2015, 119, 17344 doi: 10.1021/jp511713s[44] Hagmann J A, Li X, Chowdbury S, et al. Molecular beam epitaxy growth and structure of self-assembled Bi2Se3/Bi2MnSe4 multilayer heterostructures. New J Phys, 2017, 19, 085002 doi: 10.1088/1367-2630/aa759c[45] Zhang D, Richardella A, Rench D W, et al. Interplay between ferromagnetism, surface states, and quantum corrections in a magnetically doped topological insulator. Phys Rev B, 2012, 86, 205127 doi: 10.1103/PhysRevB.86.205127[46] Choi J, Choi S, Choi J, et al. Magnetic properties of Mn-doped Bi2Te3 and Sb2Te3. Phys Status Solidi B, 2004, 241, 1541 doi: 10.1002/pssb.200304527[47] Choi J, Choi S, Choi J, et al. Mn-doped V2VI3 semiconductors: Single crystal growth and magnetic properties. J Appl Phys, 2005, 97, 10D doi: 10.1063/1.1854451[48] Bos J W G, Lee M, Morosan E, et al. Ferromagnetism below 10 K in Mn-doped BiTe. Phys Rev B, 2006, 74, 184429 doi: 10.1103/PhysRevB.74.184429[49] Janíček P, Drašar Č, Lošt’ák P, et al. Transport, magnetic, optical and thermodynamic properties of Bi2– xMnxSe3 single crystals. Physica B, 2008, 403, 3553 doi: 10.1016/j.physb.2008.05.025[50] Hor Y S, Roushan P, Beidenkopf H, et al. Development of ferromagnetism in the doped topological insulator Bi2– xMnxTe3. Phys Rev B, 2010, 81, 195203 doi: 10.1103/PhysRevB.81.195203[51] Von Bardeleben H J, Cantin J L, Zhang D M, et al. Ferromagnetism in Bi2Se3:Mn epitaxial layers. Phys Rev B, 2013, 88, 075149 doi: http://dx.doi.org/10.1103/PhysRevB.88.075149[52] Zimmermann S, Steckel F, Hess C, et al. Spin dynamics and magnetic interactions of Mn dopants in the topological insulator Bi2Te3. Phys Rev B, 2016, 94, 125205 doi: 10.1103/PhysRevB.94.125205[53] Islam M F, Canali C M, Pertsova A, et al. Systematics of electronic and magnetic properties in the transition metal doped Sb2Te3 quantum anomalous Hall platform. Phys Rev B, 2018, 97, 155429 doi: 10.1103/PhysRevB.97.155429[54] Niu C, Dai Y, Guo M, et al. Mn induced ferromagnetism and modulated topological surface states in Bi2Te3. Appl Phys Lett, 2011, 98, 252502 doi: 10.1063/1.3601020[55] Liu Q, Liu C X, Xu C, et al. Magnetic impurities on the surface of a topological insulator. Phys Rev Lett, 2009, 102, 156603 doi: 10.1103/PhysRevLett.102.156603[56] Zhu J J, Yao D X, Zhang S C, et al. electrically controllable surface magnetism on the surface of topological insulators. Phys Rev Lett, 2011, 106, 097201 doi: 10.1103/physrevlett.106.097201[57] Sessi P, Reis F, Bathon T, et al. Signatures of Dirac fermion-mediated magnetic order. Nat Commun, 2014, 5, 5349 doi: 10.1038/ncomms6349[58] Chapler B C, Post K W, Richardella A R, et al. Infrared electrodynamics and ferromagnetism in the topological semiconductors Bi2Te3 and Mn-doped Bi2Te3. Phys Rev B, 2014, 89, 235308 doi: 10.1103/PhysRevB.89.235308[59] Collins-Mcintyre L J, Watson M D, Baker A A, et al. X-ray magnetic spectroscopy of MBE-grown Mn-doped Bi2Se3 thin films. AIP Adv, 2014, 4, 127136 doi: 10.1063/1.4904900[60] Sánchez-Barriga J, Varykhalov A, Springholz G, et al. Nonmagnetic band gap at the Dirac point of the magnetic topological insulator (Bi1− xMnx)2Se3. Nat Commun, 2016, 7, 10559 doi: 10.1038/ncomms10559[61] Liu N, Teng J, Li Y. Two-component anomalous Hall effect in a magnetically doped topological insulator. Nat Commun, 2018, 9, 1282 doi: 10.1038/s41467-018-03684-0[62] Tarasenko R, Vališka M, Vondráček M, et al. Magnetic and structural properties of Mn-doped Bi2Se3 topological insulators. Physica B, 2016, 481, 262 doi: 10.1016/j.physb.2015.11.022[63] Watson M D, Collins-McIntyre L J, Shelford L R, et al. Study of the structural, electric and magnetic properties of Mn-doped Bi2Te3 single crystals. New J Phys, 2013, 15, 103016 doi: 10.1088/1367-2630/15/10/103016[64] Li Y, Zou X, J Li, Zhou G, et al. Ferromagnetism and topological surface states of manganese doped Bi2Te3: Insights from density-functional calculations. J Chem Phys, 2014, 140, 124704 doi: 10.1063/1.4869146[65] Checkelsky J G, Ye J, Onose Y, et al. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat Phys, 2012, 8, 729 doi: 10.1038/nphys2388[66] Rosenberg G, Franz M. Surface magnetic ordering in topological insulators with bulk magnetic dopants. Phys Rev B, 2012, 85, 195119 doi: 10.1103/physrevb.85.195119[67] Liu C, Zang Yunyi, Ruan Wei, et al. Dimensional crossover-induced topological Hall effect in a magnetic topological insulator. Phys Rev Lett, 2017, 119, 176809 doi: 10.1103/PhysRevLett.119.176809[68] Kamboj S, Das S, Sirohi A, et al. Suppression of transport spin-polarization of surface states with emergence of ferromagnetism in Mn-doped Bi2Se3. J Phys Cond Matt, 2018, 30, 355001 doi: 10.1088/1361-648X/aad3ed[69] Ado I A, Dmitriev I A, Ostrovsky P M, et al. Anomalous Hall effect with massive Dirac fermions, Anomalous Hall effect with massive Dirac fermions. EPL, 2015, 111, 37004 doi: 10.1209/0295-5075/111/37004[70] Zhang J, Chang C Z, Tang P, et al. Topology-driven magnetic quantum phase transition in topological insulators. Science, 2013, 339, 1582 doi: 10.1126/science.1230905[71] Zhang Z, Feng X, Guo M, et al. Electrically tuned magnetic order and magnetoresistance in a topological insulator. Nat Commun, 2014, 5, 4915 doi: 10.1038/ncomms5915[72] Keser A C, Raimondi R, Culcer D. Sign change in the anomalous Hall effect and strong transport effects in a 2D massive Dirac metal due to spin-charge correlated disorder. arXiv: 1902.09605[73] Liu M, Zhang J, Chang C Z, et al. Crossover between weak antilocalization and weak localization in a magnetically doped topological insulator. Phys Rev Lett, 2012, 108, 036805 doi: 10.1103/PhysRevLett.108.036805[74] Li J, Li Y, Du S, et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci Adv, 2019, 5 doi: 10.1126/sciadv.aaw5685[75] Zhang D, Shi M, Zhu T, et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys Rev Lett, 2019, 122, 206401 doi: 10.1103/PhysRevLett.122.206401[76] Otrokov M M, Klimovskikh I I, et al. Prediction and observation of the first antiferromagnetic topological insulator. arXiv: 1809.07389[77] Chen B, Fei F, Zhang D, et al. Searching the Mn(Sb, Bi)2Te4 family of materials for the ideal intrinsic magnetic topological insulator. arXiv: 1903.09934[78] Deng Y, Yu Y, Shi M Z, et al. Magnetic-field-induced quantized anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. arXiv: 1904.11468[79] Liu C, Wang Y, Li H, et al. Quantum phase transition from axion insulator to Chern insulator in MnBi2Te4. arXiv: 1905.00715[80] Gong Y, Guo J, Li J, et al. Experimental realization of an intrinsic magnetic topological insulator. Chin Phys Lett, 2019, 36, 076801 doi: 10.1088/0256-307X/36/7/076801[81] Zhang S, Wang R, Wang X, et al. Experimental observation of the gate-controlled reversal of the anomalous Hall effect in the intrinsic magnetic topological insulator MnBi2Te4 device. arXiv: 1905.04839 -
Proportional views





 DownLoad:
DownLoad: