| Citation: |
Jiwen Yin, Weiping Li, Yifu Yu. Properties of a polaron in a quantum dot:a squeezed-state variational approach[J]. Journal of Semiconductors, 2013, 34(1): 012001. doi: 10.1088/1674-4926/34/1/012001
****
J W Yin, W P Li, Y F Yu. Properties of a polaron in a quantum dot:a squeezed-state variational approach[J]. J. Semicond., 2013, 34(1): 012001. doi: 10.1088/1674-4926/34/1/012001.
|
Properties of a polaron in a quantum dot:a squeezed-state variational approach
DOI: 10.1088/1674-4926/34/1/012001
More Information
-
Abstract
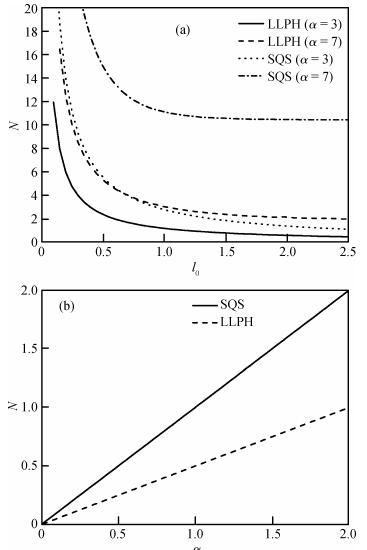
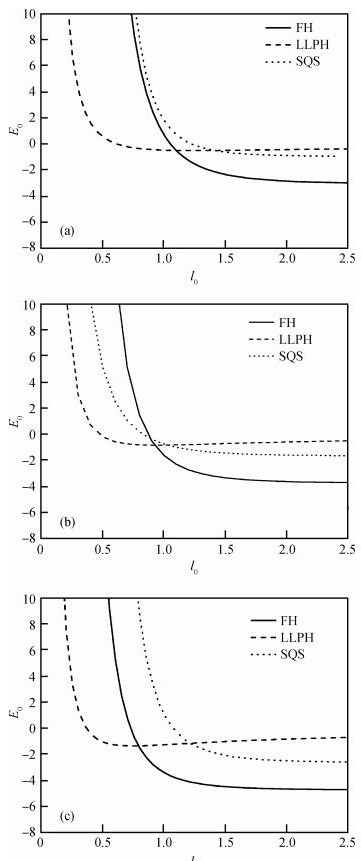
The ground-state energy and the average number of virtual phonons around the electron in a parabolic quantum dot for the entire range of the electron-phonon coupling constant are obtained using the single-mode squeezed-state variational approach. The variational approach we applied is based on two successive canonical transformations and using a displaced-oscillator type unitary transformation to deal with the bilinear terms which are usually neglected. In order to study the relationship between the ground-state energy and the average number of virtual phonons around the electron of a polaron in a parabolic quantum dot with the electron-LO-phonon coupling constant and the confinement length, numerical calculations are carried out in the electron-LO-phonon strong-and weak-coupling regions.-
Keywords:
- squeezed-state,
- quantum dot,
- polaron
-
References
[1] Haupt D, Wendler L. Resonant magnetopolaron effects in parabolic quantum wells in a tilted magnetic field. Z Phys B, 1994, 94:49 doi: 10.1007/BF01307653[2] Ercelebi A, Senger R T. Strong coupling characterisation of quasi-1D polarons in cylindrical QW-wires. Solid State Commun, 1995, 97:509[3] Chen Q H, Wang Z B, Wu F L, et al. Variational path-integral study on bound polarons in parabolic quantum dots and wires. Chin Phys Lett, 2001, 18:668 doi: 10.1088/0256-307X/18/5/315[4] De Liberato S, CIuti C. Quantum theory of intersubband polarons. Phys Rev B, 2012, 85:125302 doi: 10.1103/PhysRevB.85.125302[5] Kandemir B S. Polaronic effects on the energy spectrum of two anyons in a parabolic quantum dot. Phys Rev B, 2006, 73:115301 doi: 10.1103/PhysRevB.73.115301[6] Chen Q H, Ren Y H, Jiao Z K, et al. Polaronic effect on the binding energy of an impurity with varying position in parabolic quantum dots. Phys Lett A, 1999, 252:251 doi: 10.1016/S0375-9601(98)00949-9[7] Zhang Y, Ong W, Arakelyan I, et al. Polaron-to-polaron transitions in the radio-frequency spectrum of a quasi-two-dimensional Fermi gas. Phys Rev Lett, 2012, 108:235302 doi: 10.1103/PhysRevLett.108.235302[8] Devreese J T, Alexandrov A. Frohlich polaron and bipolaron:recent developments. Rep Prog Phys, 2009, 72:066501 doi: 10.1088/0034-4885/72/6/066501[9] Yin J W, Yu Y F, Xiao J L. Influence of the interaction between phonons and Coulomb potential on the properties of a bound polaron in a quantum dot. Chinese Journal of Semiconductors, 2007, 28:71[10] Lamouche G, Fishman G. Two interacting electrons in a three-dimensional parabolic quantum dot:a simple solution. J Phys:Condens Matter, 1998, 10:7857 doi: 10.1088/0953-8984/10/35/018[11] Li W P, Xiao J L. Influence of Coulomb potential on the properties of a polaron in a quantum dot. Chinese Journal of Semiconductors, 2007, 28:1187[12] Vasilevskiy M I, Anda E V, Makler S S. Electron-phonon interaction effects in semiconductor quantum dots:a non-perturbative approach. Phys Rev B, 2004, 70:035318 doi: 10.1103/PhysRevB.70.035318[13] Chen Q H, Ren Y H, Jiao Z K, et al. Feynman-Haken path-integral approach for polarons in parabolic quantum wires and dots. Phys Rev B, 1998, 58:16340 doi: 10.1103/PhysRevB.58.16340[14] Mukhopadhyay S, Chatterjee A. The ground and the first excited states of an electron in a multidimensional polar semiconductor quantum dot:an all-coupling variational approach. J Phys:Condens Matter, 1999, 11:2071 doi: 10.1088/0953-8984/11/9/005[15] Kervan N, Altanhan T, Chatterjee A. A variational approach with squeezed-states for the polaronic effects in quantum dots. Phys Lett A, 2003, 315:280 doi: 10.1016/S0375-9601(03)01011-9[16] Kandemir B S, Cetin A. Impurity magnetopolaron in a parabolic quantum dot:the squeezed-state variational approach. J Phys:Condens Matter, 2005, 17:667 doi: 10.1088/0953-8984/17/4/009 -
Proportional views





 DownLoad:
DownLoad: