| Citation: |
Binbin Jie, Chihtang Sah. Solid State Physics View of Liquid State Chemistry——Electrical conduction in pure water[J]. Journal of Semiconductors, 2013, 34(12): 121001. doi: 10.1088/1674-4926/34/12/121001
****
B B Jie, C T Sah. Solid State Physics View of Liquid State Chemistry——Electrical conduction in pure water[J]. J. Semicond., 2013, 34(12): 121001. doi: 10.1088/1674-4926/34/12/121001.
|
Solid State Physics View of Liquid State Chemistry——Electrical conduction in pure water
DOI: 10.1088/1674-4926/34/12/121001
More Information
-
Abstract
Engineering characterization of water has produced huge varieties of materials with special properties to meet human needs. Equilibrium properties of water-based liquids are well understood via localized atomic and molecular orbital theories. However, the mechanism of electrical conductivity of pure water has proven elusive. We show here it is trapping limited drift of positive and negative quasi-protons (or protons and proton-vacancies) on the extended water lattice, which is accounted for by the long-range correlation inherent in the Fermion (electrons and protons) and Boson (phonons) energy band theory of quasi-particles in solids, with vigorous adherence to equilibrium and nonequilibrium states. -
References
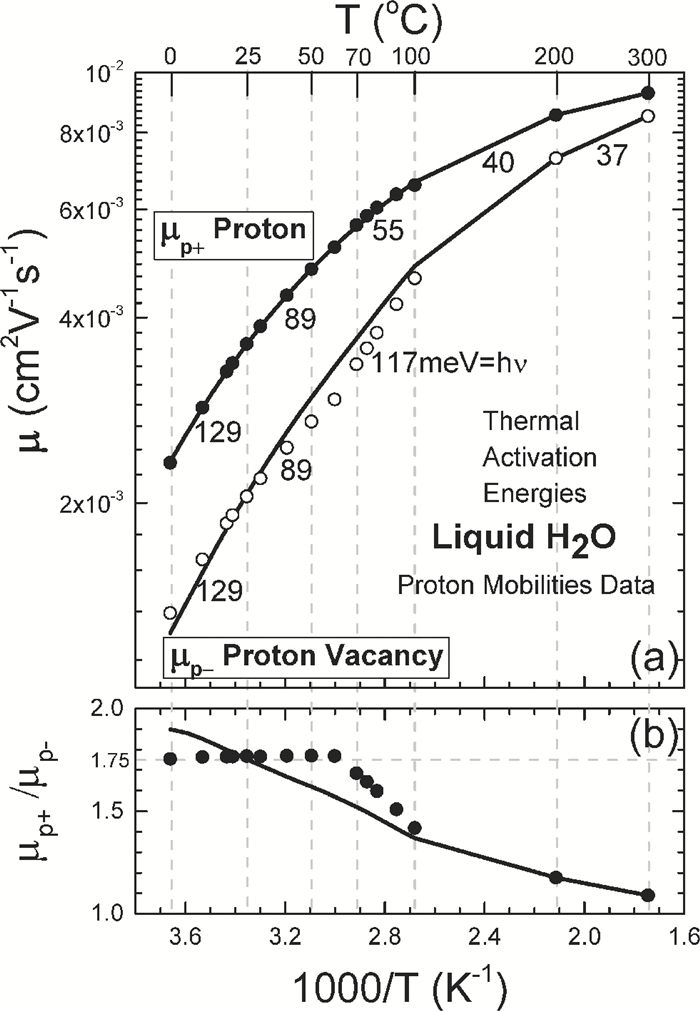
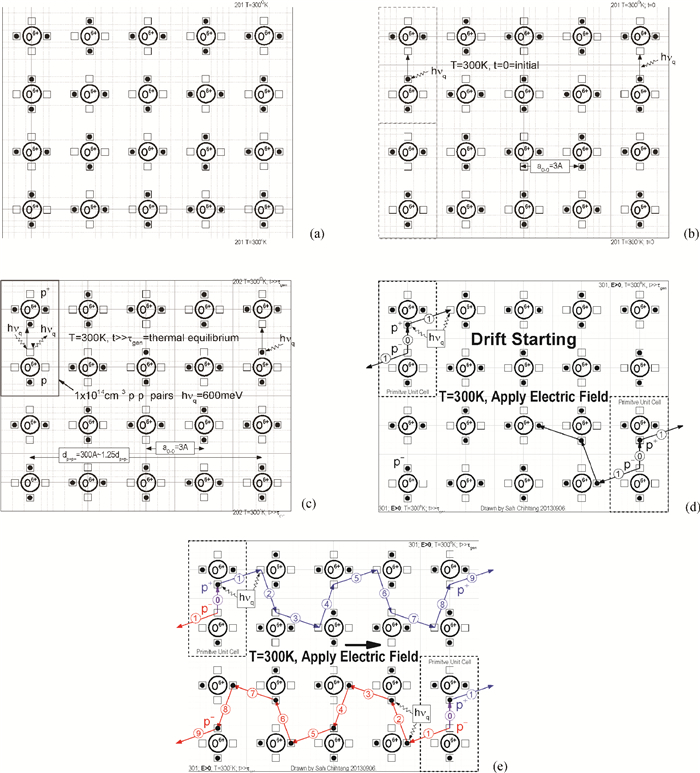
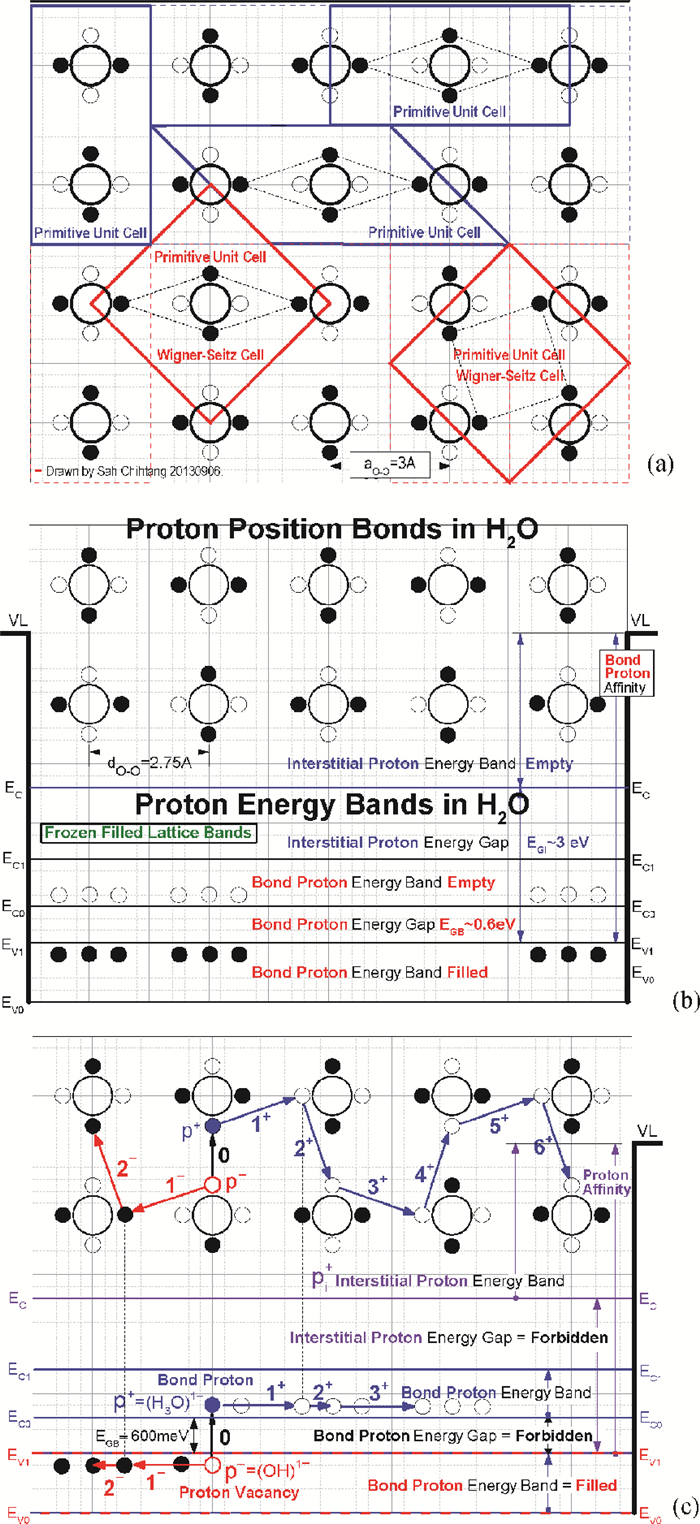
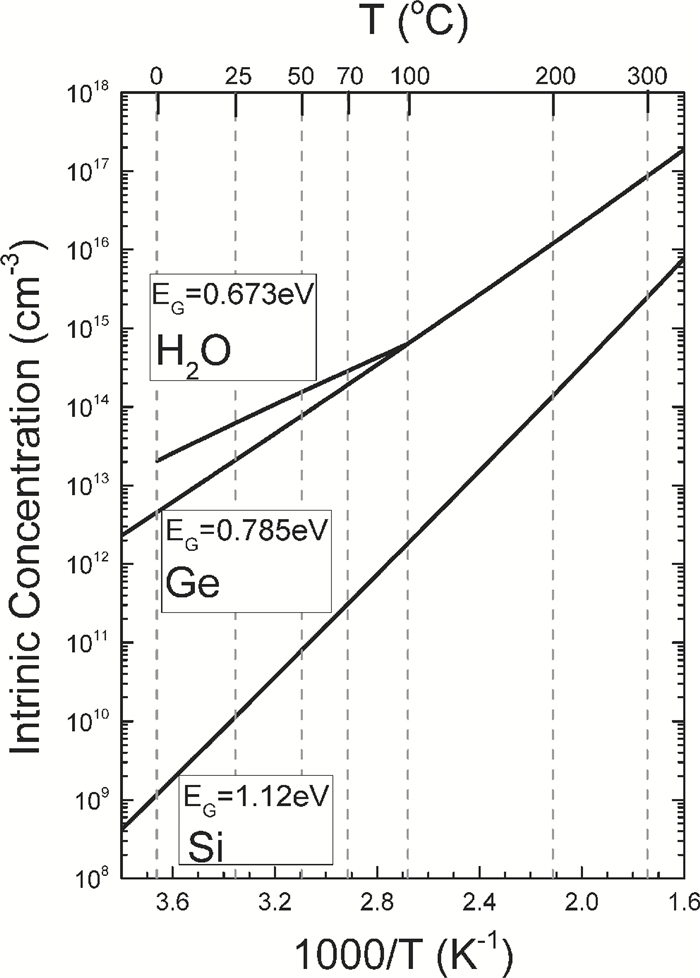
[1] J. D. Bernal and R. H. Fowler, "A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions", J. Chem. Phys. 1(8), 515-548, August, 1933. Received April 29, 1933. (University of Cambridge, England. )[2] Linus Pauling, "The structure and entropy of ice and other crystals with some randomness of atomic arrangement", J. Amer. Chem. Soc. 57(12), 2680-2684, December 1935. Received September 24, 1935. (Gates Chemical Laboratory, Caltech, Pasadena. )[3] W. F. Giauque and H. L. Hohnston, "Symmetrical and Antisymmetrical Hydrogen and the Third Law of Thermodynamics. Thermal Equilibrium and the Triple Point Pressure", J. Amer. Chem. Soc. 50, 3221-3228, 1928; J. O. Clayton and W. F. Giauque, "The Heat Capacity and Entropy of Carbon Monoxide. Heat of Vaporation. Vapor Pressures of Solid and Liquid. Free Energy to 5000°K. From Spectroscopic Data", J. Amer. Chem. Soc. 54, 2610-2626, 1932; W. W. Blue and W. F. Giauque, "The Heat Capacity and Vapor Pressure of Solid and Liquid Nitrous Oxide. The Entropy from its Band Spectrum", J. Amer. Chem. Soc. 57, 991-997, 1935. Quoted by Pauling in Ref. [2]. (UC Berkeley)[4] J. Frenkel, Kinetic Theory of Liquids, Oxford University Press, 1946 from 1943 manuscript. Dover Republication, 1955. 488pp.[5] J. M. Ziman, Models of Disorder——The theoretical physics of homogenously disordered system, Cambridge University Press, 1979. 525pp.[6] Sah Chihtang and Jie Binbin, "Semiconductor Physics View of Liquid State Chemistry", Invited Paper at the Special Session, the Sah Pen-Tung 111th Anniversary Symposium, of the 2013 National Fall-Meeting of the Chinese Physical Society, September 13-15, 2013, Xiamen University, Xiamen, Fujian, China.[7] Gilbert Newton Lewis and Merle Randall, Thermodynamics and the Free Energy of Chemical Substances, McGraw-Hill Book Company, New York, 1923. 653pp. (Textbook of graduate course in Chemistry at UC Berkeley, learned by Linda Chang in September 1959. ) See especially Chapter Ⅱ. Definitions: The Concept of Equilibrium. p. 8-20.[8] Chih-Tang Sah, Fundamentals of Solid-State Electronics, World Scientific Publishing Co. , Singapore, 1991. 1010pp. See especially Chapter 2 Homogenous Semiconductor at Equilibrium, Section 200 Introduction, 201 Homogeneous and 202 Equilibrium, p. 152-159.[9] J. L. Aragones, L. G. MacDowell, and C. Vega, "Dielectric Constant of Ices and Waters: A Lesson about Water Interactions", J. Physical Chemistry A, 115, 5754-5758, 2011. Received: June 28, 2010, Revised: September 7, 2010. Published: September 24, 2010. (U. Complutense de Madrid, Spain. )[10] Peter Atkins and Julio De Paula, Physical Chemistry, 9th Edition, W. H. Freeman and Company, New York. 2010. 972pp. One or two volumes. Figure 20. 12 on charge transport or effective motion of a proton in water on p. 762 in Volume 1, violates a number of fundamental principles governing the properties of materials. Figure 12. 38 on p. 472 gives the three normal modes of vibration of the H2O molecule, with frequencies (νg=(kg/mg)1/2/2π cg in cm-1) of 3756 and 3652 for the asymmetrical and symmetrical stretching (pumping) and 1595 for bending or breathing mode.[11] D. Eisenberg and W. Kauzmann, The Structure and Properties of Water, Clarendon Press, Oxford University Press. 1969. Published in the Oxford Classics Series, 2005. Reprinted 2011. 296pp. Figures on p. 227 give the proton and proton vacancy transport model in water, closest to our model, however, they require additional rotation of the whole water molecule and they do not satisfy the translational symmetry of the extended water lattice, which involves two water molecules in the primitive cubic unit cell and four water molecules in the primitive hexagonal unit cell. The highly localized molecular orbital theory does not account for the correlated motion of the water molecules in the extended volume of the water or liquid H2O.[12] N. H. Fletcher, The Chemical Physics of Ice (Cambridge Monographs on Physics), Cambridge University Press. 1970. Digital version 2009. Made in the U. S. A. Lexington, KY, 03 September 2013. 271pp. N. H. Fletcher, "Structural aspects of the ice-water system", Report Progress Physics, 34, 913-994, 1971.[13] Peter V. Hobbs, Ice Physics, Oxford Classic Texts in the Physical Sciences, Oxford University Press, Oxford, 1974. Paperback 2010. 837 pp. Figure 1. 1 on p. 6 gives the three vibration normal modes of the water molecule, with their vibrational frequency or wave number formulas for an anharmonic oscillator given by Eqs. (1. 7) and (1. 9), and ground state energy given by Eq. (1. 8), the anharmonicity constants derived in 1956 by Benedict in Table 1. 1, with the numerical results (cm-1) of 3574. 32, 3754. 32 and 1596. 71 and 575 meV, respectively. A detailed description of the Pauling zero-point entropy calculation for the 1h hexagonal ice crystal is given in section 1. 2. 2 on p. 25-33, including the 1964 analytical solution of Hollins that took into account of the correlated motion of the smallest hexagonal ring structure containing six H2O molecules ring, and the interference between rings described by DiMarzio and Sillingerin, giving a slight increase of the residual entropy, the factor of 1/729, which was extended numerically by Nagle in 1966 giving S0=Rloge[(3/2)×(1+1/729)2 +0. 002732]=3. 4103 J/mol-degree almost in exact agreement with the experimental value obtained in constant pressure heat capacity measurements made by Giauque and Stout in 1936, added by Simon and extended to nearly 0°K in 1966 by Flubacher et al. in 1960, giving a calculated experimental value of 3. 41 by Eisenberg and Kauzmann in 1969, as indicated in Fig. 5. 7 on p. 363 and Table 5. 4 on p. 364, which ascertain the position of the two protons in the 1h hexagonal ice, which is more than 70% of ice.[14] Victor F. Petrenko (Thayer School of Engineering, Dartmouth College, Hanover, New Hampshire) and Robert W. Whitworth (School of Physics and Astronomy, The University of Birmingham), Physics of Ice, Oxford University Press, Oxford, 1999. Reprinted 2003. 373 pp. The three vibrational modes of H2O molecule in dilute gas, shown in Fig. 3. 9, are given in both units, ν1=3656. 65 cm-1=453. 370 meV, ν2=1594. 59 cm-1=197. 705 meV, and ν3=3757. 79 cm-1=465. 909 meV, whereas, the two stretching modes, ν1 and ν3, depend on the force constant to stretch the O: H bond, while the bending mode, ν2, depends on the force constant to change the H: O: H bond angle. The two force-constant phonon energy band diagram (hbar ω q-q) computed by Faure in 1969 is given in Fig. 3. 12 on p. 55, showing the 12 branches from the four H2O molecules in the primitive translation unit cell of the hexagonal ice (1h) crystal, in which each H2O molecule vibrates as a unit, or as a particle (or a point) of mass MH2O=18, with the zone-center longitudinal phonons at q=0 of 29. 7 meV, 22. 7 meV and 18. 8 meV. The 24 vibrational branches due to the 3-dimensional vibrations around each two protons' oxygen atomic core, via the Born-Oppenheimer adiabetic notion, of the 8 hydrogen ions, or protons, in the translational primitive unit cell, can be scaled by the square-root of the (force/mass) ratio: ν H/νH2O=[(kH/MH)1/2/(kH2O/MH2O)1/2] (MH2O/MH)1/2=(18/1)1/2=4. 243, for those optical modes in which the two protons move separately or in opposite directions. For those acoustic modes in which the two protons move together or in the same direction, the single proton mass is replaced by the two proton mass and the frequencies are reduced by 21/2. Since the force constants are not constant, which we assumed constant in this mass-scaling, we won't add the small correction via center of the mass, to this adiabatic estimate, (1+ MH/MH2O)1/2=(1+1/18)1/2=1. 0274. These give the energies of the zone center longitudinal phonons of 29. 7×4. 243=126 meV, 22. 7×4. 243=96 meV and 18. 8×4. 243=80 meV for the two protons vibrating separately, and 21/2=1. 414 less for the two protons vibrating together, 89 meV, 68 meV and 56 meV. These theoretical estimate by mass scaling, compare favorably with the experimental energies of the phonon absorbed in order to detrap proton or thermally release the trapped proton from the trap, which are: 129 meV (0-20℃) and 89 meV (25-55℃) for both p+ and p-, and 55 meV for p+ and 117 meV for p- (60-100℃), from the thermally activated mobilities of proton, p+, and proton vacancy, p-, which we discovered while plotting the published experimental data, described in the text. These water phonons could correspond to the antisymmetric and symmetric stretching modes, and the bending mode of vibration of the two protons in the isolated H2O.[15] George Malenkov, "Liquid water and ices: understanding the structure and physical properties", J. Physics: Condens. Matter 21, 283101(35 pages). Received 13 November 2007. Published, 18 June 2009. (AN Frumkin Institute of Physical Chemistry and Electrochemistry, Leninskii Prospect, Moscow, Russiaule.[16] John C. Slater, Introduction to Chemical Physics, McGraw-Hill Book company, 1939. Dover edition, 1970. 521pp. The number of vibrational degree of freedom is given on p. 140 for the molecule (dilute gas) H2O, H: O: H, of the temperate equivalent vibration frequencies of 5170° K and 5400° K for the symmetrical or pull-pull and the asymmetrical or push-pull pumping (stretching) modes, and 2290° K for the breathing (bending) mode, which are lowered in liquid H2O or water due to the presence of neighboring molecules which slow down the vibrations. (M. I. T. )[17] John C. Slater, Quantum Theory of Molecules and Solids Volume 3 Insulators, Semiconductors and Metals, McGraw-Hill Book Company, New York, 1967. 549pp. (M. I. T. )[18] John C. Slater, Quantum Theory of Matter, McGraw-Hill Book Company, New York, First Edition, 1951. Second Edition, 1968. 763pp. (M. I. T. )[19] William Shockley, Electrons and Holes in Semiconductors, D. Van Nostrand Company, Inc. 1950. (Bell Telephone Laboratories. )[20] N. B. Hannay (Editor), Semiconductors, Reinhold Publishing Company, New York, Chapman & Hall, Ltd, London. 767pp, 1959. This was a first public disclosure of the similarity between water and semiconductor. See Fig. 5. 1 on p. 196 of Chapter 5, Defect Interactions in Semiconductors, by C. S. Fuller. (Bell Telephone Laboratories. )[21] H. S. Harned, and B. B. Owen, The Physical Chemistry of Electrolytic Solutions, 3rd Edition, Reinhold, New York, 1958. 2nd Edition, 1949; 1st Edition 1943(Yale University), published by the American Chemical Society in its Monograph Series. Pp. 231, 233, 638, 645, as quoted by Truman S. Light, "Temperature Dependence and Measurement of Resistivity of Pure Water", Analytical Chemistry 56, 1138-1142, 1984.[22] Afred Pebler, "Temperature Correction for the Specific Conductivity of Dilute Aqueous Ammonia Solutions", Analytical Chemistry, 53, 1134-1136, 1981. (60℃ to 90℃) Westinghouse Research and Development Laboratory, Pittsburgh, Penn.[23] S. Alvin, S. Quist and William L. Marshall, "Assignment of Limiting Equivalent Conductances for Single Ions to 400℃", J. Physical Chemistry, 69, 2984-2987, 1985. (100℃, 200℃ and 300℃) Reactor Chemistry Division, Oak Ridge National Laboratory.[24] Truman S. Light, Stuart Licht, Anthony C. Bevilacqua, and Kenneth R. Morash, "The Fundamental Conductivity and Resistivity of Water", Electrochemical and Solid-State Letters, 8(1), E16-E19, 2005. doi: 10.1149/1.1836121 -
Proportional views





 DownLoad:
DownLoad: