1. Introduction

Graphene is an exciting material for fundamental and applied solid-state physics research due to its special electronic structure and massless Dirac-fermion behavior^[1-9]. Novel condensed matter effects arising from its unique two-dimensional (2D) energy dispersion, along with superior properties, make it a promising material for the next generation of faster and smaller electronic devices. However, with 2D graphene being a zero-gap semiconductor, its use in an active electronic device such as a field effect transistor (FET) lacks an essential feature, namely, a band gap around the Fermi level. To solve this problem, various schemes have been presented to open a band gap in graphene^[10-15]. One scheme proposed by Eduardo is that the band structure of bilayer graphene can be controlled externally by applying a gate bias, and the value of the gap as a function of the electronic density can be extracted using a tight binding model^[10]. Another suggestion is the creation of gaps through confinement. Band-gap engineering of graphene nanoribbons (GNRs) has been experimentally demonstrated, and a GNR-based field-effect transistor (with a width of several tens of nanometers down to 2 nm) has been characterized^{[12, 13, 15]}. Chemical modification provides an effective way to manipulate the electronic properties of graphene-based materials. Doping graphene chemically with nitrogen has been studied both theoretically and experimentally^[16-22]. The interplay between nitrogen lone-pair electrons and the graphene $\pi$ system changes the electronic property and chemical reactivity. Recently, two stable, ordered N-doped graphene structures, C$_{3}$N and C$_{12}$N, were theoretically revealed through the cluster–expansion technique and particle-swarm optimization method^[23]. Calculations show that the band gap of C$_{3}$N and C$_{12}$N are 0.96 eV and 0.98 eV, respectively, which is a good band gap for many semiconductors.

Graphene-oxide (G-O) has recently emerged as a new carbon-based nanoscale material^{[24, 25]}. It contains a range of oxygen functional groups, which renders it a good candidate for many applications, such as sensors and flexible transparent conductive electrodes^[26]. However, previous studies have indicated that G-O is an insulator with poor electronic properties. Thus, control oxidation of G-O by various chemical and thermal reduction treatments plays an important role that provides tunability for the electronic and mechanical properties. Recently, a new material called graphene monoxide (GMO) has been experimentally developed, which has a quasi-hexagonal unit cell and an unusually high 1 : 1 C : O ratio^[27]. The calculation based on density functional theory (DFT) shows that the direct band gap of GMO is $\sim$ 0.9 eV^[27]. The semiconducting properties of GMO suggest that this new material might be useful for various electronic applications, which may hold the key towards graphene-based electronics. However, the ground state and optical properties of this new type of semiconductor are still far from clear. 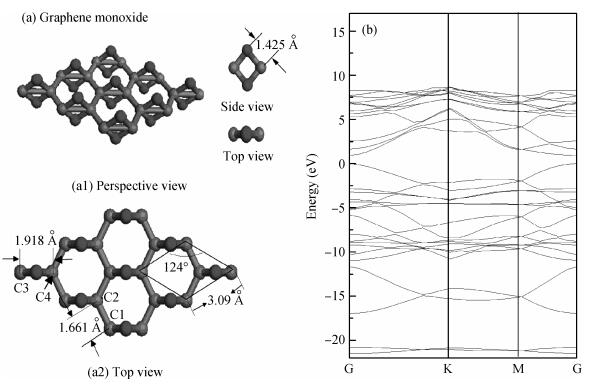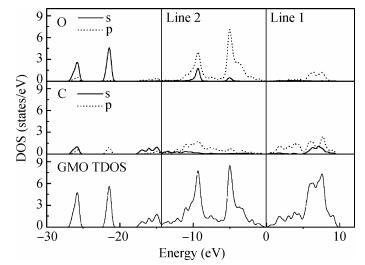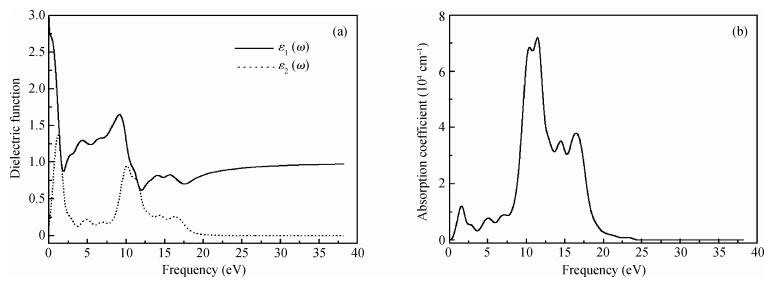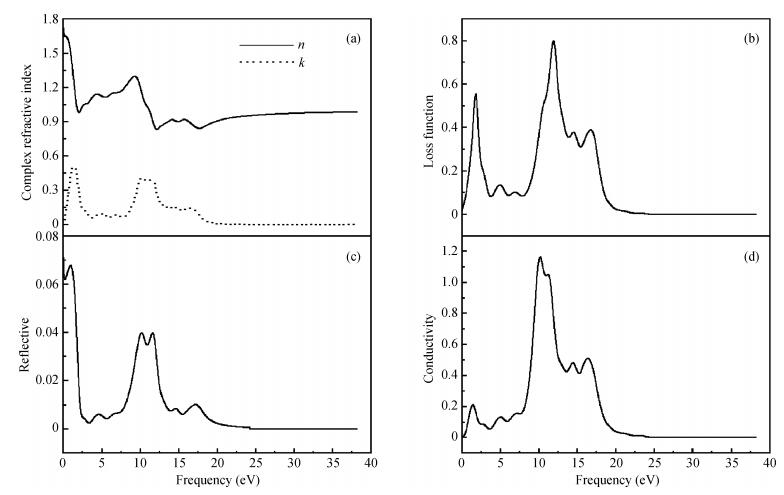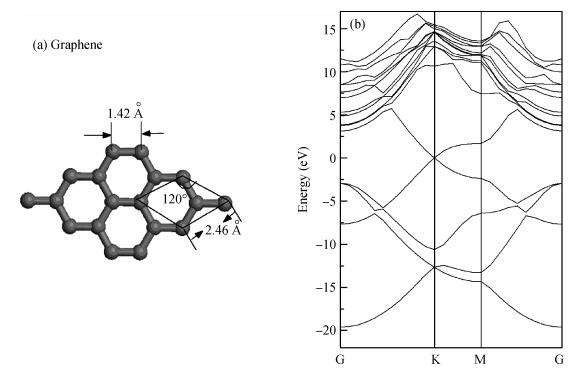In this paper, we present a detailed theoretical study about the electronic and optical properties of GMO, which are critical to the potential applications in electronic devices.

2. Computational method

A detailed description of the crystal structural data of GMO can be derived from Ref. [27]. Guided by the experiment, the lattice and electronic structure of GMO are calculated within the frame of the DFT. CASTEP is used to optimize the initial structure. The interactions between the valence electrons and the ionic core are represented by ultra-soft pseudopotentials, and the exchange-correlation energy is calculated by the generalized gradient approximation (GGA) in terms of Perdew-Burke-Ernzerl (PBE). The valence electron configuration considered in this paper includes O 2s$^{2}$2p$^{4}$ and C 2s$^{2}$2p$^{2}$. Lots of converging tests are performed, and there is a cutoff energy of 380 eV and 10 $\times$ 10 $\times$ 1 Monkhorst-Pack $k$-points for integrals in the Brillouin zone. The structure is considered to be in equilibrium when the average force acting on the ions is finally reduced to 5.0 $\times$ 10$^{-7}$ eV/atom.

3. Results and discussion

3.1 Geometry structure and Muliken's population analysis

In order to compare the electronic structure of graphene and GMO, we start our simulations with the case of graphene. The calculated lattice structure and band structure for graphene are shown in Fig. 1. From Fig. 1(b), one can see that the band gap of graphene is zero, which shows that graphene is a zero-gap semiconductor. The optimized structure and calculated band structure for graphene are in agreement with the theoretical results reported elsewhere^[28], and confirm the accuracy and reliability of our calculations. Next, a detailed simulation is considered for GMO. We construct the crystal structure directed by Ref. [27] and optimize it using CASTEP. Muliken's population analysis is calculated to investigate the electronic structure of GMO, as listed in Table 1. Detailed results about the bond parameters for GMO are marked in Fig. 2(a), and found to be consistent with the experiment^[27]. Compared with graphene, the bond length of C–C is changed from 1.42 to 1.661 Å and 1.918 Å, respectively. The primitive vectors increase from 2.46 to 3.09 Å, and the angle between them is 120$^\circ$ versus 124$^\circ$. Thus, the structure of GMO no longer has the three-fold symmetry of the graphene lattice. Consequently, the space group for graphene belongs to D$_{\rm 6h}$ symmetry, while the GMO corresponds to D$_{\rm 2h}$ symmetry. In addition, it is evident from Table 1 that the charge of O and C in GMO is –0.45 and 0.45, which is related to the electron gains and losses. For this reason, the total electron number for C decreases from 4.0 to 3.55, and increases to 6.45 for O.

3.2 Band structure and density of states

The band structure for the GMO calculation is then obtained, and the corresponding band gap is 0.952 eV. This result is closer to the calculated result of ~0.90 eV reported in Ref. [27]. Figure 2(b) illustrates the band structure of GMO, which shows that it is a direct band gap semiconductor. The valence band maximum and the conduction minimum are located at the G point. Fortunately, a band gap is opened in graphene-based material by the chemical functionalization, which has an important significance to the development of electronic devices. Figure 3 shows the total density of states (TDOS) for GMO and the partial DOS plots of C and O, where line 1 represents the Fermi level. One can see that the peaks of TDOS on the left side of line 2 are mainly provided by the O2s and C2s orbital. As the energy is greater than –14.2 eV, corresponding to the right side of line 2, the curve in TDOS mostly consists of the O2p and C2p orbital. Interestingly, the valance band near the Fermi level is mainly composed of O2s2p, while the conduction band is attributed to the 2s and 2p orbital of C.

3.3 Optical properties

The study of the optical functions helps give a better understanding of the electronic structure, which is useful for the design and manufacture of the photoelectron devices. The optical properties may be received from the complex dielectric function, $\varepsilon (\omega )=\varepsilon _{1}(\omega )$ $+$ i$\varepsilon _{2}(\omega)$. The imaginary part of the dielectric constant $\varepsilon_{2}(\omega)$ can be calculated from the momentum matrix elements between the occupied and the unoccupied electronic states. The real part $\varepsilon_{1}(\omega)$ is derived from the imaginary part $\varepsilon_2(\omega)$ by the Kramers-Kronig transformation. Besides, other optical constants, such as the absorption coefficient $\alpha$, complex refractive index $n_{\rm c}= n$ – i$k$, with $n$, $k$ the refractive index and extinction coefficient, loss-function $\beta$, reflectivity $R$ and conductivity $\sigma$, are calculated by the following equations^[29].

$\varepsilon _2 (\omega )=\frac{2e^2\pi }{\Omega \varepsilon _0 }\sum\limits_{k, v, c} {\left| {\psi _k^c } \right|} ur\left| {\psi _k^v } \right|\delta (E_k^c -E_k^v -E),$

(1)

$\varepsilon _1 (\omega )=1+\frac{2}{\pi }P\int_0^\infty {\frac{{\omega }'\varepsilon _2 ({\omega }')}{{\omega }'^2-\omega ^2}} {\rm d}{\omega }',$

(2)

$\alpha (\omega )=\sqrt 2 \left[\sqrt {\varepsilon _1 ^2(\omega )+\varepsilon _2 ^2(\omega )}-\varepsilon _1 (\omega)\right]^{1/2},$

(3)

$n(\omega )=\frac{\sqrt 2}{2}\left[\sqrt {\varepsilon _1 ^2(\omega )+\varepsilon _2 ^2(\omega )} +\varepsilon _1 (\omega)\right]^{1/2},$

(4)

$k(\omega )=\frac{\sqrt 2}{2}\left[\sqrt {\varepsilon _1 ^2(\omega )+\varepsilon _2 ^2(\omega )}-\varepsilon _1 (\omega)\right]^{1/2},$

(5)

$\beta (\omega )={\rm Im}\left(\frac{-1}{\varepsilon (\omega)}\right),$

(6)

$R(\omega )=\left| {\frac{\sqrt {\varepsilon (\omega )} -1}{\sqrt {\varepsilon (\omega )} +1}} \right|^2,$

(7)

$\sigma (\omega )={\rm Re}\left(-{\rm i}\frac{\omega }{4\pi }(\varepsilon (\omega )-1)\right),$

(8)

where $u$ is the vector defining the polarization of the incident electric field, $\omega$ is the light frequency, $e$ is the electric charge, and $\psi _k^c$ and $\psi _k^v$ are the conduction and valence band wave functions at $k$, respectively. The $P$ in front of the integral means the principal value.

Figure 4 depicts the dielectric function and the absorption coefficient of GMO for photon frequency up to 40 eV. The solid and dotted lines in Fig. 4(a) show the imaginary and real part of the dielectric function, respectively. It is observed that the static constant $\varepsilon_{1}$(0) is close to 3, and the curve drops rapidly till $\omega$ $=$ 1.82 eV. In the range of 1.82–12.02 eV, $\varepsilon_{1}(\omega )$ rises slowly and then decreases sharply. With a further increase in frequency, the value of $\varepsilon_{1}(\omega )$ increases slowly and up to a constant $\varepsilon_{1}(\omega )$ $=$ 0.97 when $\omega$ $>$ 35 eV. Two obvious peaks of the $\varepsilon_{2}(\omega )$ can be found, which are always related to electron excitation. The imaginary part of dielectric function $\varepsilon_{2}(\omega )$ vanishes with the frequency $\omega$ $>$ 24.9 eV. It is noteworthy that the $\varepsilon_{1}(\omega )$ $>$ 0 and $\varepsilon_{2}(\omega)$ $=$ 0 values mean that the region is a transparent area. If we refer to the absorption parameter as shown in Fig. 4(b), the optical absorption edge is about 0.95 eV, which corresponds to the GMO band gap in our calculation.

The other optical constants, including the complex refractive index $n$ and $k$, loss-function $\beta$, reflectivity $R$ and conductivity $\sigma$ are displayed in Fig. 5. The static refractive index $n$ of GMO shown in Fig. 5(a) has a value of 1.7. In Fig. 5(b), the electron energy function describes the energy loss of a fast electron traversing a material with the change in frequency. Two apparent peaks of loss function are located at 1.80 and 11.93 eV, and are associated with the plasma frequency. Figure 5(c) shows the reflectivity spectra as a function of light frequency. The spectra shows that the reflectivity $R$ $=$ 0 when the frequency $\omega$ $>$ 24.9 eV, which proves once again the existence of the transparent area. Figure 5(d) depicts the change in conductivity caused by the frequency, which is the physical basis to the application in optical electronic devices. The curve is similar to the absorption coefficient in Fig. 4(b), and even the corresponding location for the peaks and valleys is the same. The minimum value is 3.79 eV, while the maximum point occurs at 10.16 eV. As $\omega$ $>$ 24.9 eV, its value is equal to zero.

4. Conclusion

In summary, the electronic structure and optical properties of GMO are studied based on density functional theory. Directed by the experimental data of GMO, we use CASTEP to calculate the Muliken population and the band structure. The results show that the geometric structure changes significantly from graphene to GMO. As shown in Figs. 1 and 2, the magnitude of the lattice parameters increases from 2.46 to 3.09 Å, and the angle between them is 120$^\circ$ of an ideal hexagonal lattice of graphene versus 124$^\circ$ in GMO. In particular, the band structure indicates that GMO is semiconducting with a direct band gap of 0.952 eV. This new material has potential for various electronic applications that may hold the key towards graphene-based electronics. Further, the optical properties, e.g. the dielectric function, absorption coefficient, complex refractive index, loss-function, reflectivity and conductivity are analyzed in detail.