| Citation: |
Yamin Zhang, Shiwei Feng, Hui Zhu, Xueqin Gong, Bing Deng, Lin Ma. Self-heating and traps effects on the drain transient response of AlGaN/GaN HEMTs[J]. Journal of Semiconductors, 2014, 35(10): 104003. doi: 10.1088/1674-4926/35/10/104003
****
Y M Zhang, S W Feng, H Zhu, X Q Gong, B Deng, L Ma. Self-heating and traps effects on the drain transient response of AlGaN/GaN HEMTs[J]. J. Semicond., 2014, 35(10): 104003. doi: 10.1088/1674-4926/35/10/104003.
|
Self-heating and traps effects on the drain transient response of AlGaN/GaN HEMTs
DOI: 10.1088/1674-4926/35/10/104003
More Information
-
Abstract
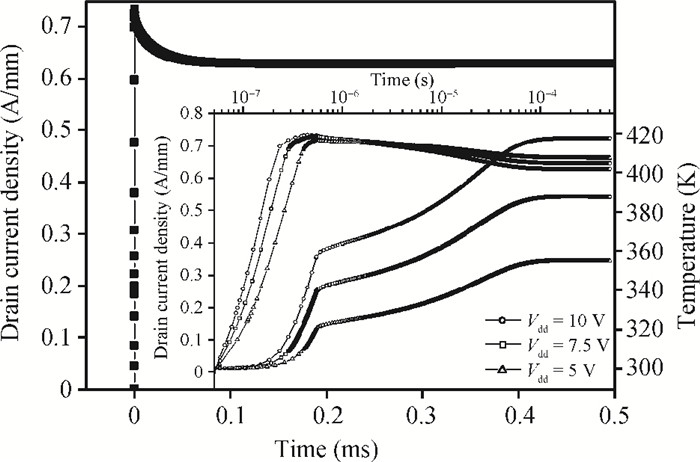
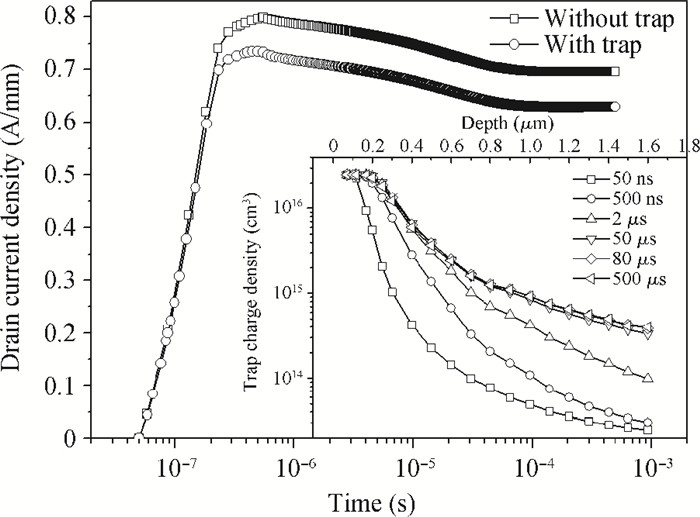
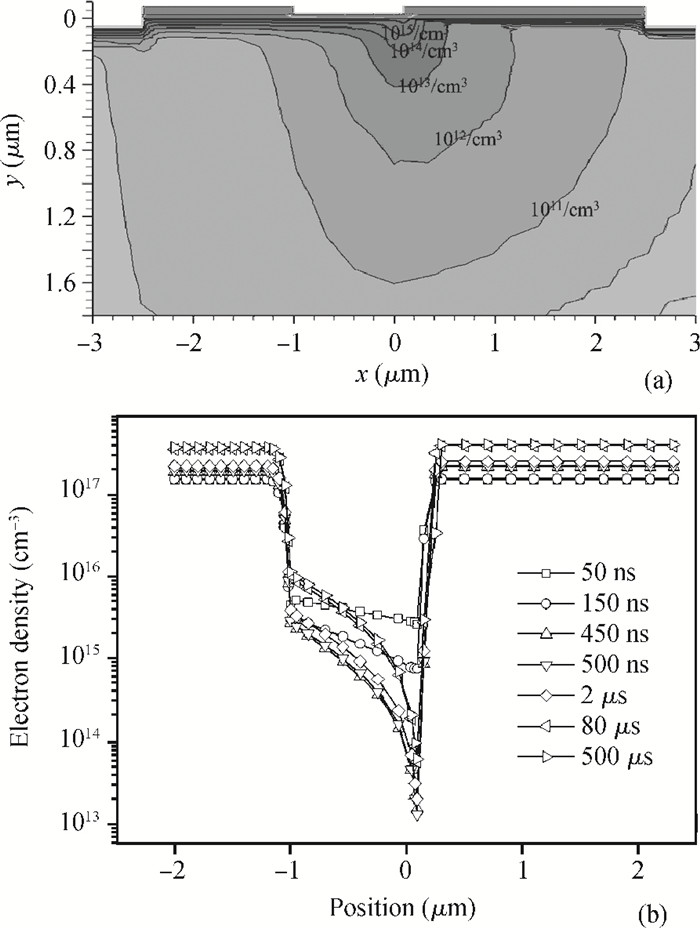
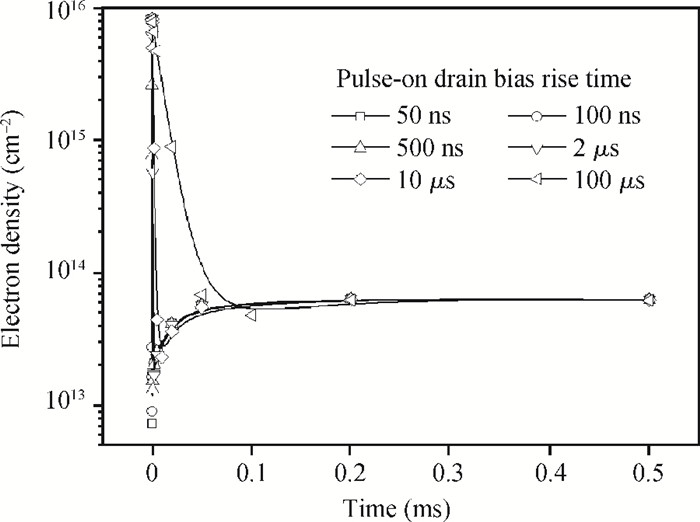
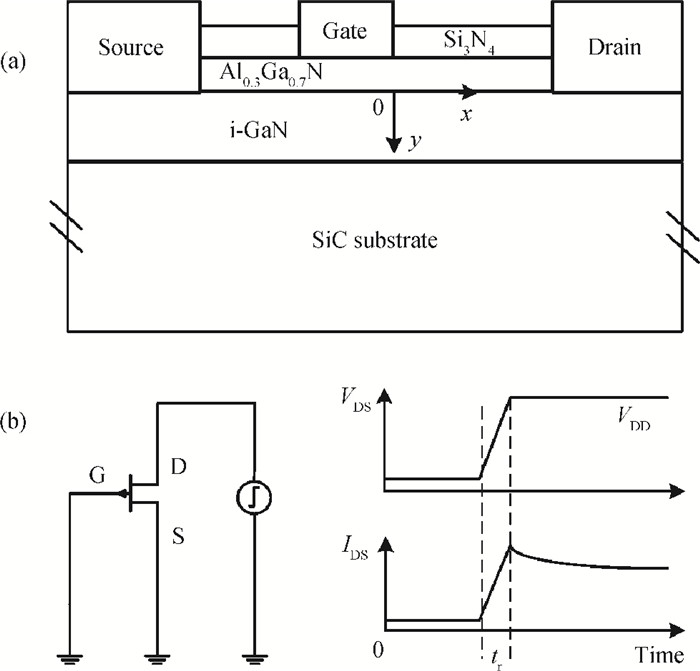
The effects of self-heating and traps on the drain current transient responses of AlGaN/GaN HEMTs are studied by 2D numerical simulation. The variation of the drain current simulated by the drain turn-on pulses has been analyzed. Our results show that temperature is the main factor for the drain current lag. The time that the drain current takes to reach a steady state depends on the thermal time constant, which is 80 μs in this case. The dynamics of the trapping of electron and channel electron density under drain turn-on pulse voltage are discussed in detail, which indicates that the accepter traps in the buffer are the major reason for the current collapse when the electric field significantly changes. The channel electron density has been shown to increase as the channel temperature rises. -
References
[1] Wang C, Chong C, He Y, et al. Breakdown voltage and current collapse of F-plasma treated AlGaN/GaN HEMTs. Journal of Semiconductors, 2014, 35(1):014008 doi: 10.1088/1674-4926/35/1/014008[2] Chu F, Chen C, Liu X. Breakdown voltage enhancement of AlGaN/GaN high electron mobility transistors by polyimide/chromium composite thin film passivation. Journal of Semiconductors, 2014, 35(3):034007 doi: 10.1088/1674-4926/35/3/034007[3] Yang Z, Wang J, Xu Z, et al. Analysis of AlGaN/GaN high electron mobility transistors failure mechanism under semi-on DC stress. Journal of Semiconductors, 2014, 35(1):014007 doi: 10.1088/1674-4926/35/1/014007[4] Zhang Y, Feng S, Zhu H, et al. Effect of self-heating on the drain current transient response in AlGaN/GaN HEMTs. IEEE Electron Device Lett, 2014, 35(3):345 doi: 10.1109/LED.2014.2300856[5] Tirado J M, Sánchez-Rojas J L, Izpura J I. Trapping effects in the transient response of AlGaN/GaN HEMT devices. IEEE Trans Electron Devices, 2007, 54(3):410 doi: 10.1109/TED.2006.890592[6] Wang X D, Hu W D, Chen X S, et al. The study of self-heating and hot-electron effects for AlGaN/GaN double-channel HEMTs. IEEE Trans Electron Devices, 2012, 59(5):1393 doi: 10.1109/TED.2012.2188634[7] Zhang W, Zhang Y, Mao W, et al. Influence of the interface acceptor-like traps on the transient response of AlGaN/GaN HEMTs. IEEE Electron Device Lett, 2013, 34(1):45 doi: 10.1109/LED.2012.2227235[8] Miccoli C, Martino V C, Reina S, et al. Trapping and thermal effects analysis for AlGaN/GaN HEMTs by means of TCAD simulations. IEEE Electron Device Lett, 2013, 34(9):1121 doi: 10.1109/LED.2013.2274326[9] Hu W D, Chen X S, Yin F, et al. Two-dimensional transient simulations of drain lag and current collapse in GaN-based high-electron-mobility transistors. J Appl Phys, 2009, 105(8):084502 doi: 10.1063/1.3106603[10] Turin V O, Balandin A A. Electrothermal simulation of the self-heating effects in GaN-based field-effect transistors. J Appl Phys, 2006, 100(5):054501 doi: 10.1063/1.2336299[11] Hu W D, Chen X S, Quan Z J, et al. Self-heating simulation of GaN-based metal-oxide-semiconductor high-electron-mobility transistors including hot electron and quantum effects. J Appl Phys, 2006, 100(7):074501 doi: 10.1063/1.2354327[12] Zhang Y, Feng S, Zhu H, et al. Two-dimensional transient simulations of the self-heating effects in GaN-based HEMTs. Microelectron Reliab, 2013, 53(5):694 doi: 10.1016/j.microrel.2013.02.004[13] Meneghesso G, Meneghini M, Bisi D, et al. Trapping phenomena in AlGaN/GaN HEMTs:a study based on pulsed and transient measurements. Semicond Sci Technol, 2013, 28(7):074021 doi: 10.1088/0268-1242/28/7/074021[14] Manoi A, Pomeroy J W, Killat N, et al. Benchmarking of thermal boundary resistance in AlGaN/GaN HEMTs on SiC substrates:implications of the nucleation layer microstructure. IEEE Electron Device Lett, 2010, 31(12):1395 doi: 10.1109/LED.2010.2077730[15] Wang L, Fjeldly T A, Iniguez B, et al. Self-heating and kink effects in a-Si:H thin film transistors. IEEE Trans Electron Devices, 2000, 47(2):387 doi: 10.1109/16.822285[16] Wang M, Chen K J. Kink effect in AlGaN/GaN HEMTs induced by drain and gate pumping. IEEE Electron Device Lett, 2011, 32(4):482 doi: 10.1109/LED.2011.2105460[17] Nakkala P, Martin A, Campovecchio M, et al. Pulsed characterisation of trapping dynamics in AlGaN/GaN HEMTs. Electron Lett, 2013, 49(22):1406 doi: 10.1049/el.2013.2304[18] Maeda N, Tsubaki K, Saitoh T, et al. High-temperature electron transport properties in AlGaN/GaN heterostructures. Appl Phys Lett, 2001, 79(11):1634 doi: 10.1063/1.1400779 -
Proportional views





 DownLoad:
DownLoad: