| Citation: |
Hui Guo, Yaqiu Zhao, Yuming Zhang, Xianbao Ling. Influence of N-type doping on the oxidation rate in n-type 6H-SiC[J]. Journal of Semiconductors, 2015, 36(1): 013006. doi: 10.1088/1674-4926/36/1/013006
****
H Guo, Y Q Zhao, Y M Zhang, X B Ling. Influence of N-type doping on the oxidation rate in n-type 6H-SiC[J]. J. Semicond., 2015, 36(1): 013006. doi: 10.1088/1674-4926/36/1/013006.
|
Influence of N-type doping on the oxidation rate in n-type 6H-SiC
DOI: 10.1088/1674-4926/36/1/013006
More Information
-
Abstract
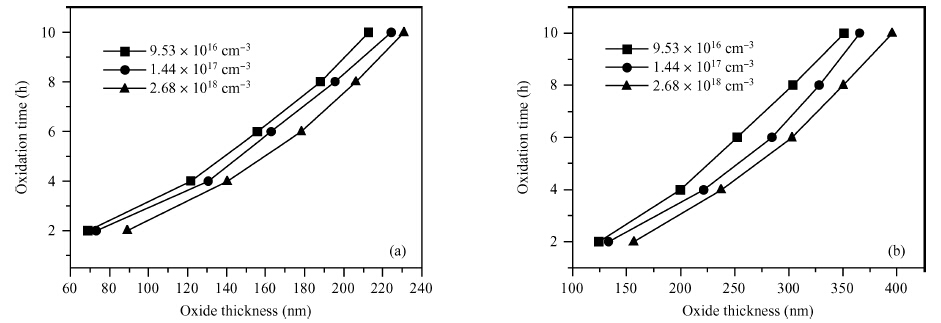
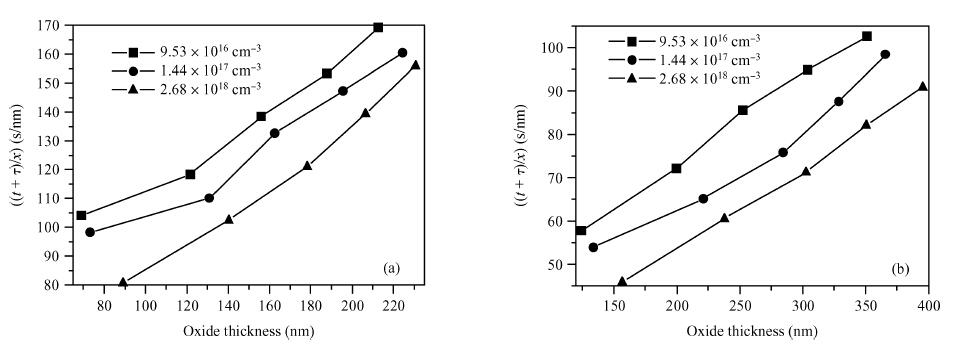
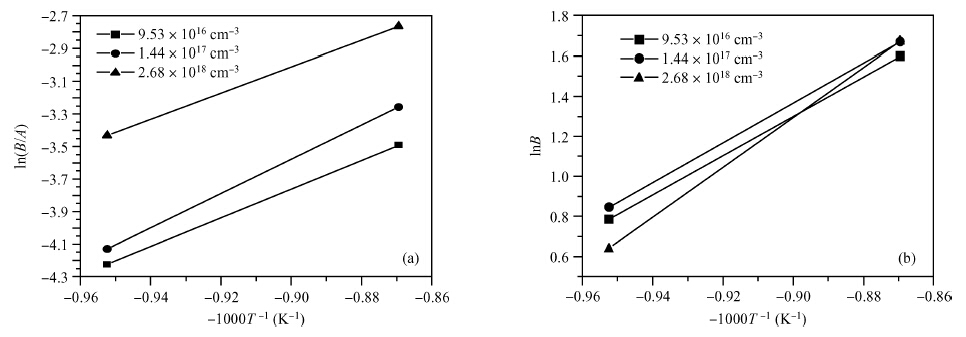
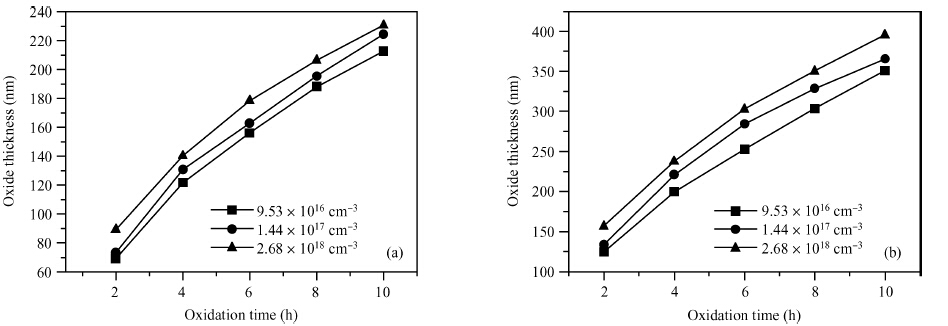
The doping dependence of dry thermal oxidation rates in n-type 6H-SiC was studied. The oxidation temperature ranged from 1050 to 1150 ℃ and the nitrogen doping concentration ranged from 9.53 × 1016, 1.44 × 1017, to 2.68 × 1018 cm-3. By combining the modified deal-grove model and Arrhenius equation, the linear and parabolic rate constants, and their corresponding activation energies were extracted. The results show that: higher temperature corresponded to thicker oxides; dry thermal oxidation rate in n-type 6H-SiC depended on the doping concentration; both linear-rate-constant and parabolic-rate-constant increased with the doping concentration; the parabolic activation energy increased from 0.082 to 0.104 eV, both linear and parabolic activation energies increasing with the doping concentration; and, the parabolic pre-exponential factor increased from 2.6 × 104 to 2.7 × 105 nm2/s, both linear and parabolic pre-exponential factor increasing with doping concentration. Moreover, the experiment also illustrated that it is unreasonable to use a variation of the Arrhenius activation energy to explain the doping dependence of thermal oxidation on SiC. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] -
Proportional views





 DownLoad:
DownLoad: