| Citation: |
Jihai Duan, Chuang Lan, Weilin Xu, Baolin Wei. An OTA-C filter for ECG acquisition systems with highly linear range and less passband attenuation[J]. Journal of Semiconductors, 2015, 36(5): 055006. doi: 10.1088/1674-4926/36/5/055006
****
J H Duan, C Lan, W L Xu, B L Wei. An OTA-C filter for ECG acquisition systems with highly linear range and less passband attenuation[J]. J. Semicond., 2015, 36(5): 055006. doi: 10.1088/1674-4926/36/5/055006.
|
An OTA-C filter for ECG acquisition systems with highly linear range and less passband attenuation
DOI: 10.1088/1674-4926/36/5/055006
More Information
-
Abstract
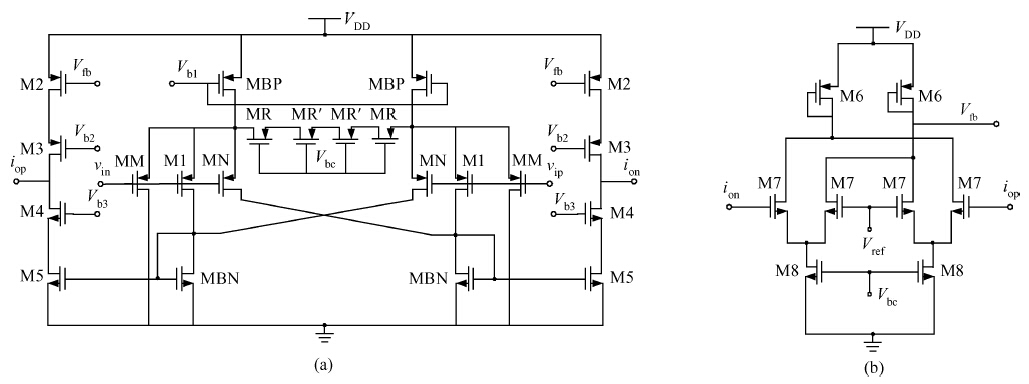
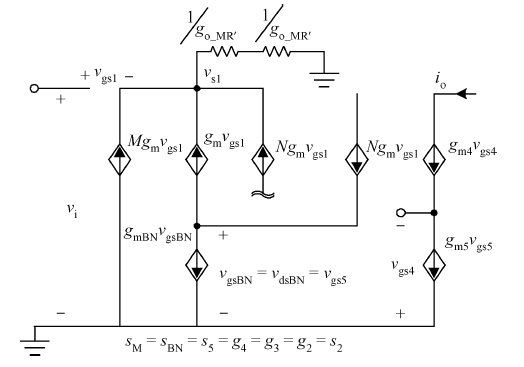
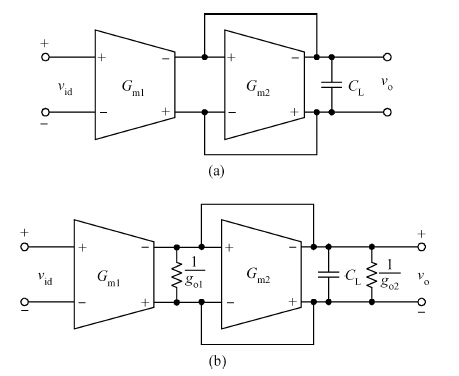
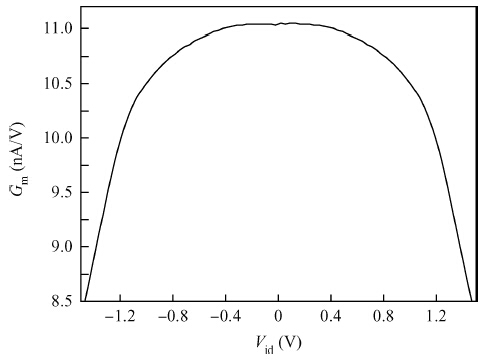
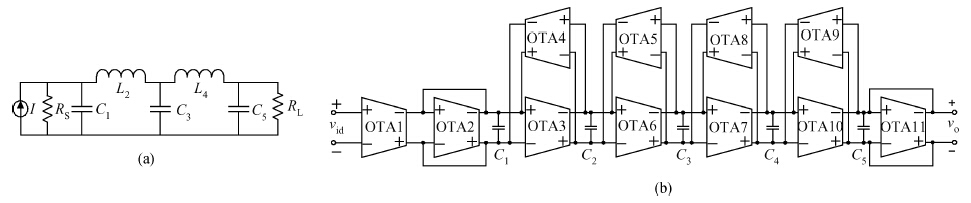
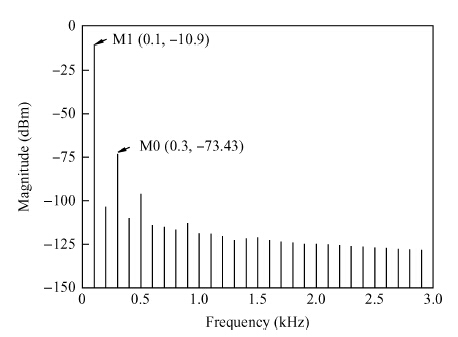
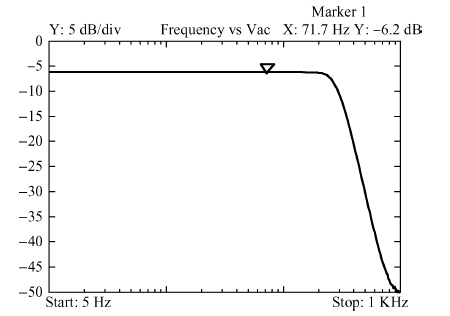
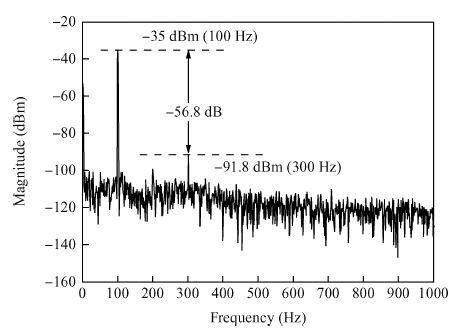
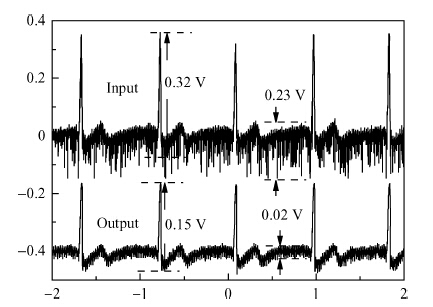
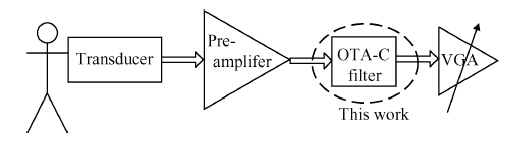
A fifth order operational transconductance amplifier-C (OTA-C) Butterworth type low-pass filter with highly linear range and less passband attenuation is presented for wearable bio-telemetry monitoring applications in a UWB wireless body area network. The source degeneration structure applied in typical small transconductance circuit is improved to provide a highly linear range for the OTA-C filter. Moreover, to reduce the passband attenuation of the filter, a cascode structure is employed as the output stage of the OTA. The OTA-based circuit is operated in weak inversion due to strict power limitation in the biomedical chip. The filter is fabricated in a SMIC 0.18-μ m CMOS process. The measured results for the filter have shown a passband gain of -6.2 dB, while the -3-dB frequency is around 276 Hz. For the 0.8 VPP sinusoidal input at 100 Hz, a total harmonic distortion (THD) of -56.8 dB is obtained. An electrocardiogram signal with noise interference is fed into this chip to validate the function of the designed filter. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] -
Proportional views





 DownLoad:
DownLoad: