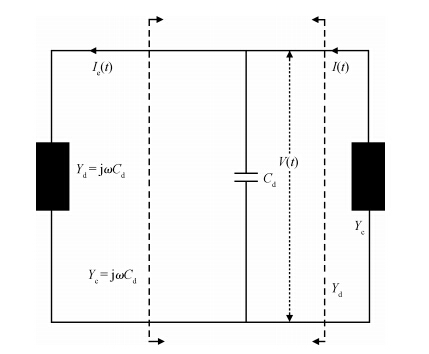
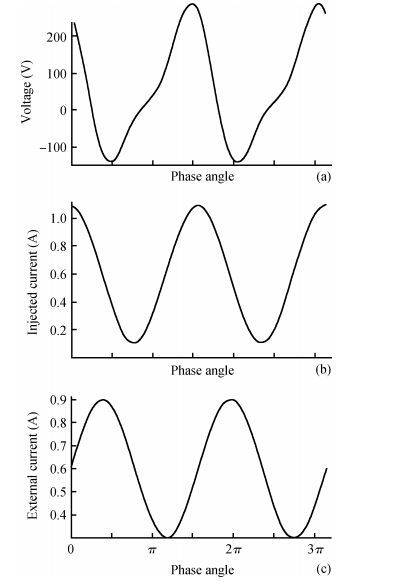
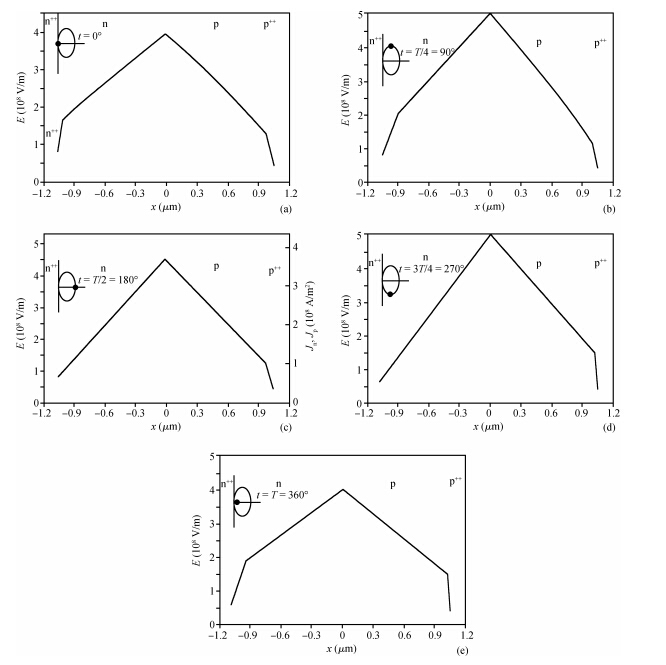
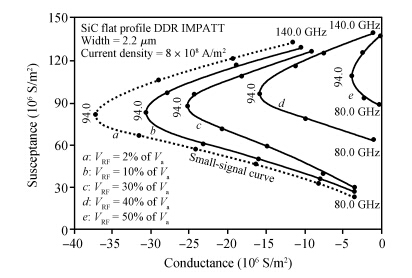
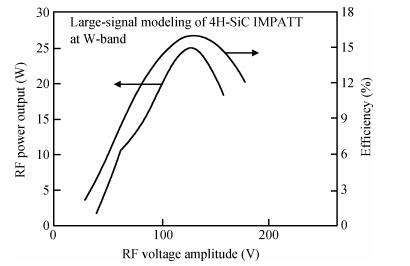
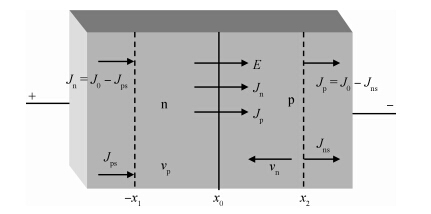
Abstract: A full-scale, self-consistent, non-linear, large-signal model of double-drift hetero-structure IMPATT diode with general doping profile is derived. This newly developed model, for the first time, has been used to analyze the large-signal characteristics of hexagonal SiC-based double-drift IMPATT diode. Considering the fabrication feasibility, the authors have studied the large-signal characteristics of Si/SiC-based hetero-structure devices. Under small-voltage modulation (～ 2%, i.e. small-signal conditions) results are in good agreement with calculations done using a linearised small-signal model. The large-signal values of the diode's negative conductance (5 × 10⁶S/m²), susceptance (10.4 × 10⁷ S/m^2}), average breakdown voltage (207.6 V), and power generating efficiency (15%, RF power: 25.0 W at 94 GHz) are obtained as a function of oscillation amplitude (50% of DC breakdown voltage) for a fixed average current density. The large-signal calculations exhibit power and efficiency saturation for large-signal (> 50%) voltage modulation and thereafter decrease gradually with further increasing voltage-modulation. This generalized large-signal formulation is applicable for all types of IMPATT structures with distributed and narrow avalanche zones. The simulator is made more realistic by incorporating the space-charge effects, realistic field and temperature dependent material parameters in Si and SiC. The electric field snap-shots and the large-signal impedance and admittance of the diode with current excitation are expressed in closed loop form. This study will act as a guide for researchers to fabricate a high-power Si/SiC-based IMPATT for possible application in high-power MM-wave communication systems.

Key words: Si/SiC hetero-structure double drift diode, full-scale large-signal modelling, high-power, parasitic effects, noise-analysis