| Citation: |
Kenyu Osada, Hiroyasu Katsuno, Toshiharu Irisawa, Yukio Saito. Scaling relation of domain competition on (2+1)-dimensional ballistic deposition model with surface diffusion[J]. Journal of Semiconductors, 2016, 37(9): 092001. doi: 10.1088/1674-4926/37/9/092001
****
K. Osada, H Katsuno, T Irisawa, Y Saito. Scaling relation of domain competition on (2+1)-dimensional ballistic deposition model with surface diffusion[J]. J. Semicond., 2016, 37(9): 092001. doi: 10.1088/1674-4926/37/9/092001.
|
Scaling relation of domain competition on (2+1)-dimensional ballistic deposition model with surface diffusion
DOI: 10.1088/1674-4926/37/9/092001
More Information
-
Abstract
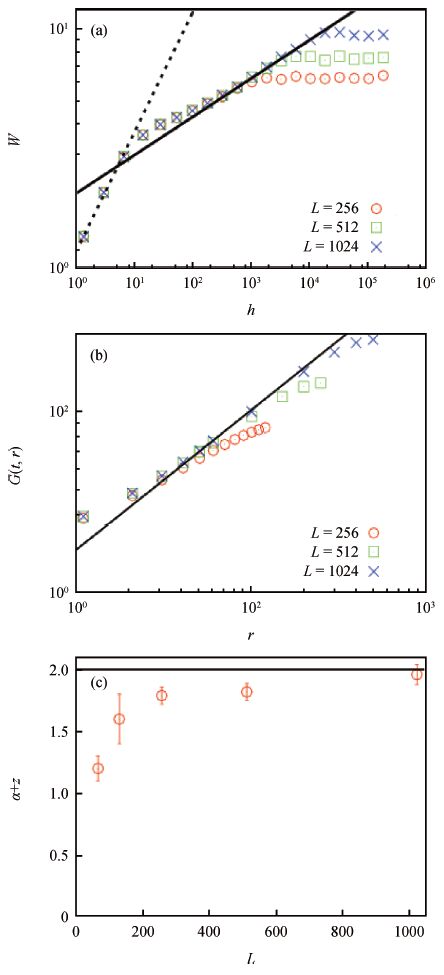
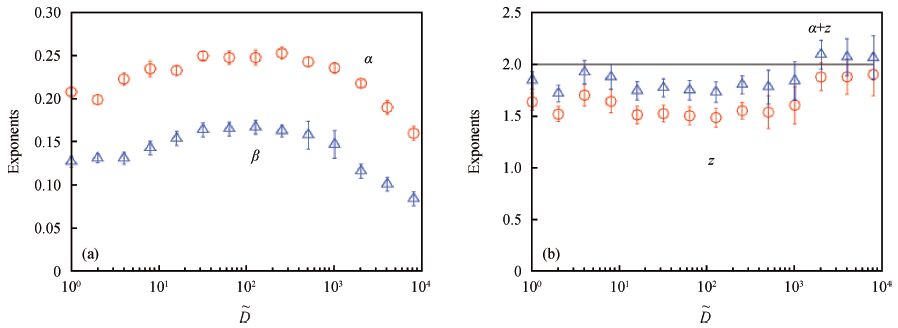
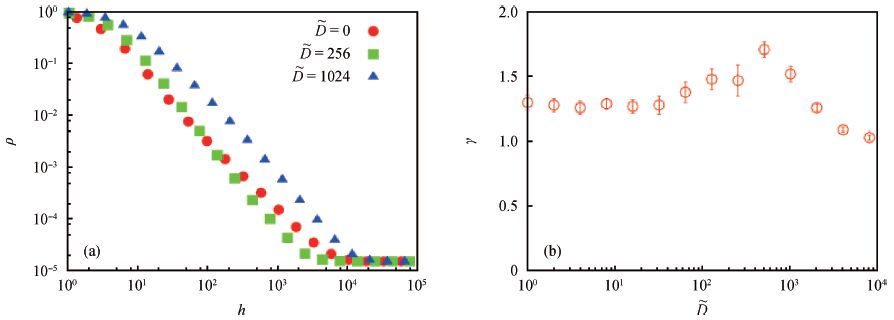
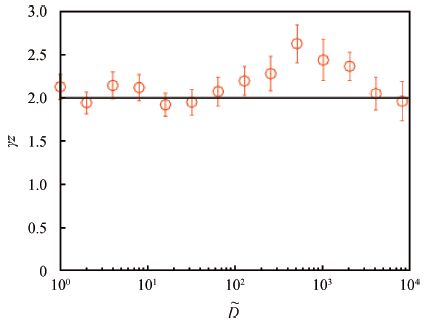
During heteroepitaxial overlayer growth multiple crystal domains nucleated on a substrate surface compete with each other in such a manner that a domain covered by neighboring ones stops growing. The number density of active domains ρ decreases as the height h increases. A simple scaling argument leads to a scaling law of ρ~h-γ with a coarsening exponent γ=d/z, where d is the dimension of the substrate surface and z the dynamic exponent of a growth front. This scaling relation is confirmed by performing kinetic Monte Carlo simulations of the ballistic deposition model on a two-dimensional (d=2) surface, even when an isolated deposited particle diffuses on a crystal surface. -
References
[1] Hayes W, Stoneham A M. Defects and defect processes in nonmetallic solids. New York: John Wiley & Sons, 1985[2] Amano H, Sawai N, Akasaki I, et al. Metalorganic vapor phase epitaxial growth of a high quality GaN film using an AlN buffer layer. Appl Phys Lett, 1986, 48: 353 doi: 10.1063/1.96549[3] Nakamura S. GaN growth using GaN buffer layer. Jpn J Appl Phys, 1991, 30: L1705 doi: 10.1143/JJAP.30.L1705[4] Zheleva T S, Nam O H, Bremser M D, et al. Dislocation density reduction via lateral epitaxy in selectively grown GaN structures. Appl Phys Lett, 1997, 71: 2472 doi: 10.1063/1.120091[5] Hersee S D, Sun X Y, Wang X, et al. Nanoheteroepitaxial growth of GaN on Si nanopillar arrays. J Appl Phys, 2005, 97: 124308 doi: 10.1063/1.1937468[6] Saito Y, Omura S. Domain competition during ballistic deposition: effect of surface diffusion and surface patterning. Phys Rev E, 2011, 84: 021601 http://cn.bing.com/academic/profile?id=2062908940&encoded=0&v=paper_preview&mkt=zh-cn[7] Family F, Vicsek T. Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. J Phys A, 1985, 18(2): L75 doi: 10.1088/0305-4470/18/2/005[8] Barabási A L, Stanley H E. Fractal concepts in surface growth. Cambridge: Cambridge University Press, 1995[9] Kardar M, Parisi G, Zhang Y C. Dynamic scaling of growing interfaces. Phys Rev Lett, 1986, 56: 889 doi: 10.1103/PhysRevLett.56.889[10] Farnudi B, Vvdensky D D. Large-scale simulations of ballistic deposition: the approach to asymptotic scaling. Phys Rev E, 2011, 83: 020103(R) http://cn.bing.com/academic/profile?id=2070087653&encoded=0&v=paper_preview&mkt=zh-cn[11] Alves S G, Oliveira T J, Ferreira S C. Origins of scaling corrections in ballistic growth models. Phys Rev E, 2014, 90: 052405 doi: 10.1103/PhysRevE.90.052405[12] Ballestad A, Ruck B J, Admcyk M, et al. Evidence from the surface morphology for nonlinear growth of epitaxial GaAs films. Phys Rev Lett, 2001, 86: 2377 doi: 10.1103/PhysRevLett.86.2377[13] Halpin-Healy T, Palasantzas G. Universal correlators and distributions as experimental signatures of (2+1)-dimensional Kardar-Parisi-Zhang growth. Euro Phys Lett, 2014, 105: 50001 doi: 10.1209/0295-5075/105/50001[14] Michely T, Krug J. Island, mounds and atoms: patterns and processes in crystal growth far from equilibrium. Berlin: Springer-Verlag, 2004[15] Ehrlich G, Hudda F G. Atomic view of surface self-diffusion: tungsten on tungsten. J Chem Phys, 1966, 44: 1039 doi: 10.1063/1.1726787[16] Schwoebel R L, Shipsey E J. Step motion on crystal surfaces. J Appl Phys, 1966, 37: 3682 doi: 10.1063/1.1707904[17] Bortz A B, Kalos M H, Lebowitz J L. A new algorithm for Monte Carlo simulation of Ising spin system. J Comput Phys, 1975, 17: 10 doi: 10.1016/0021-9991(75)90060-1[18] Saberi A A, Dashti-Naserabadi H, Rouhani S. Classification of (2+1)-dimensional growing surfaces using Schramm-Loewner evolution. Phys Rev E, 2010, 82: 020101(R) http://cn.bing.com/academic/profile?id=2081862734&encoded=0&v=paper_preview&mkt=zh-cn[19] Oliveira T J, Alves S G, Ferreira S C. Kardar-Parisi-Zhang universality class in (2+1) dimensions: universal geometry-dependent distributions and finite-time corrections. Phys Rev E, 2013, 87: 040102(R) http://cn.bing.com/academic/profile?id=2012768116&encoded=0&v=paper_preview&mkt=zh-cn[20] Moser K, Wolf D E. Numerical solution of the Kardar-Parisi-Zhang equation in one, two and three dimensions. Physica A, 1991, 178: 215 doi: 10.1016/0378-4371(91)90017-7[21] Tamborenea P, Das Sarma S. Surface-diffusion-driven kinetic growth on one-dimensinoal substrate. Phys Rev E, 1993, 48: 2575 doi: 10.1103/PhysRevE.48.2575 -
Proportional views





 DownLoad:
DownLoad: