| Citation: |
D. Ajitha, K.V. Ramanaiah, V. Sumalatha. An enhanced high-speed multi-digit BCD adder using quantum-dot cellular automata[J]. Journal of Semiconductors, 2017, 38(2): 024002. doi: 10.1088/1674-4926/38/2/024002
****
D. Ajitha, K.V. Ramanaiah, V. Sumalatha. An enhanced high-speed multi-digit BCD adder using quantum-dot cellular automata[J]. J. Semicond., 2017, 38(2): 024002. doi: 10.1088/1674-4926/38/2/024002.
|
An enhanced high-speed multi-digit BCD adder using quantum-dot cellular automata
DOI: 10.1088/1674-4926/38/2/024002
More Information
-
Abstract
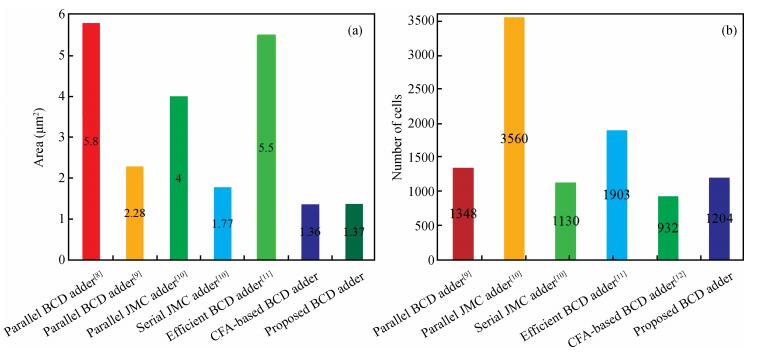
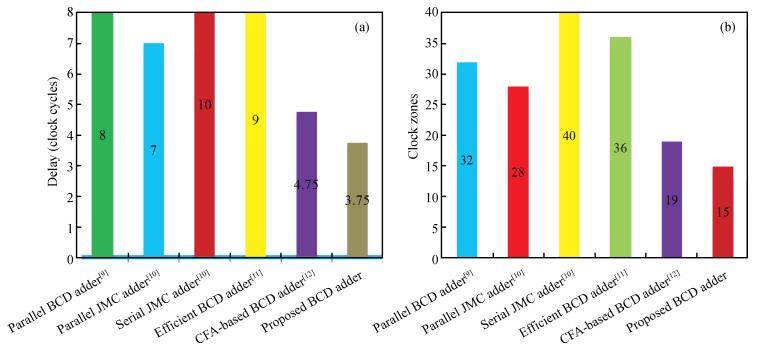
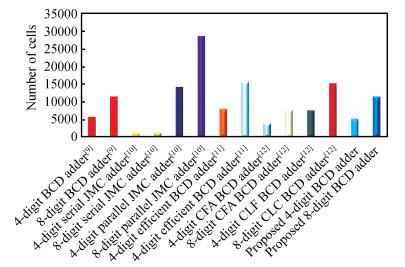
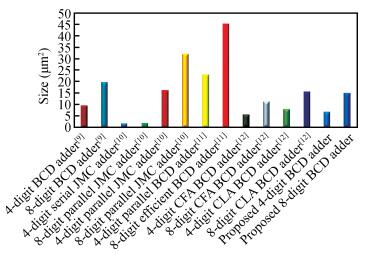
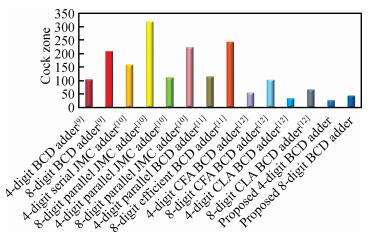
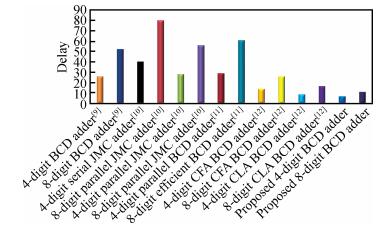
The advent of development of high-performance, low-power digital circuits is achieved by a suitable emerging nanodevice called quantum-dot cellular automata (QCA). Even though many efficient arithmetic circuits were designed using QCA, there is still a challenge to implement high-speed circuits in an optimized manner. Among these circuits, one of the essential structures is a parallel multi-digit decimal adder unit with significant speed which is very attractive for future environments. To achieve high speed, a new correction logic formulation method is proposed for single and multi-digit BCD adder. The proposed enhanced single-digit BCD adder (ESDBA) is 26% faster than the carry flow adder (CFA)-based BCD adder. The multi-digit operations are also performed using the proposed ESDBA, which is cascaded innovatively. The enhanced multi-digit BCD adder (EMDBA) performs two 4-digit and two 8-digit BCD addition 50% faster than the CFA-based BCD adder with the nominal overhead of the area. The EMDBA performs two 4-digit BCD addition 24% faster with 23% decrease in the area, similarly for 8-digit operation the EMDBA achieves 36% increase in speed with 21% less area compared to the existing carry look ahead (CLA)-based BCD adder design. The proposed multi-digit adder produces significantly less delay of (N-1)+3.5 clock cycles compared to the N*One digit BCD adder delay required by the conventional BCD adder method. It is observed that as per our knowledge this is the first innovative proposal for multi-digit BCD addition using QCA. -
References
[1] Lent C S, Tougaw P, Porod W, et al. Quantum cellular automata. Nanotechnology, 1993, 4:49 doi: 10.1088/0957-4484/4/1/004[2] Aspray W. Computing before computers. Ames, Iowa:Iowa State University Press, 1990[3] Zuras D, Cowlishaw M, Aiken A, et al. IEEE standard for floating-point arithmetic. IEEE Std 754, 2008:1[4] Cowlishaw M F. Decimal floating-point:algorism for computers. 16th IEEE Symposium on Computer Arithmetic, 2003:104[5] Schwarz E M, Check M A, Shum C L, et al. The microarchitecture of the IBM eServer z900 processor. IBM J Res Dev, 2002, 46(45):381 https://www.cl.cam.ac.uk/teaching/0607/CompArch/ibmz90-schwarz.pdf[6] Pudi V, Sridharan K. Efficient design of a hybrid adder in quantum-dot cellular automata. IEEE Trans Very Large Scale Integration (VLSI) Syst, 2011, 19(9):1535 doi: 10.1109/TVLSI.2010.2054120[7] Pudi V, Sridharan K. New decomposition theorems on majority logic for low-delay adder designs in quantum dot cellular automata. IEEE Trans Circuits Syst Ⅱ, 2012, 59(10):678 https://www.researchgate.net/publication/260667145_New_Decomposition_Theorems_on_Majority_Logic_for_Low-Delay_Adder_Designs_in_Quantum_Dot_Cellular_Automata[8] Taghizadeh M, Askari M, Fardad K. BCD computing structures inquantum-dot cellular automata. IEEE International Conference on Computer and Communication Engineering, 2008:1042[9] Kharbash F, Chaudhry G M. The design of quantum-dot cellular automata decimal adder. IEEE International Conference on Multitopic, 2008:71[10] Gladshtein M. Quantum-dot cellular automata serial decimal adder. IEEE Trans Nanotechnol, 2011, 10(6):1377 doi: 10.1109/TNANO.2011.2138714[11] Shah N A, Khanday F A, Bangi Z A. Quantum cellular automata based efficient BCD adder structure. Commun Inform Sci Management Eng, 2012, 2(2):11[12] Liu W, Lu L, Swartzlander E E. Cost-efficient decimal adder design in quantum-dot cellular automata. IEEE International Symposium on Circuits and Systems, 2012:1347[13] Aggarwal M, Agarwal A, Mehra M R. 4-input decimal adder using 90 nm CMOS technology. IOSR J Eng, 2013, 3(5):2250[14] Perri S, Corsonello P, Cocorullo G. Area-delay efficient binary adders in QCA. IEEE Trans Very Large Scale Integration (VLSI) Syst, 2014, 22(5):1174 doi: 10.1109/TVLSI.2013.2261831[15] Cho H, Swartzlander E E Jr. Adder and multiplier design in quantum-dot cellular automata. IEEE Trans Comput, 2009, 58(6):721 doi: 10.1109/TC.2009.21[16] Lent C S, Tougaw P D. Lines of interacting quantum-dot cells:a binary wire. J Appl Phys, 1993, 74(10):6227 doi: 10.1063/1.355196[17] Walus K, Schulhof G, Jullien G A. High level exploration of quantum-dot cellular automata (QCA). Thirty-Eighth Asilomar IEEE Conference on Signals Systems and Computers, 2004:30[18] Kim K, Wu K, Karri R. Towards designing robust QCA architectures in the presence of sneak noise paths. IEEE Conference on Design Automation and Test, 2005:1214[19] Kim K, Wu K, Karri R. The robust QCA adder designs using composable QCA building blocks. IEEE Trans Comput-Aided Des Integr Circuits Syst, 2007, 26(1):176 doi: 10.1109/TCAD.2006.883921[20] Gin A, Tougaw P D, Williams S. An alternative geometry for quantum-dot cellular automata. J Appl Phys, 1999, 85(12):8281 doi: 10.1063/1.370670[21] Walus K, Jullien G A. Design tools for an emerging SoC technology:quantum-dot cellular automata. Proc IEEE, 2006, 94(6):1225 doi: 10.1109/JPROC.2006.875791[22] Kumar R, Ghosh B, Gupta S. Adder design using a 5-input majority gate in a novel "multilayer gate design paradigm" for quantum dot cellular automata circuits. J Semicond, 2015, 36(4):045001 doi: 10.1088/1674-4926/36/4/045001[23] Niemier M T, Kogge P M. Problems in designing with QCAs:Layout D timing. Int J Circuit Theory Appl, 2001, 29(1):49 doi: 10.1002/(ISSN)1097-007X -
Proportional views





 DownLoad:
DownLoad: