| Citation: |
Huifang Xu, Yuehua Dai. Two-dimensional analytical model of double-gate tunnel FETs with interface trapped charges including effects of channel mobile charge carriers[J]. Journal of Semiconductors, 2017, 38(2): 024004. doi: 10.1088/1674-4926/38/2/024004
****
H F Xu, Y H Dai. Two-dimensional analytical model of double-gate tunnel FETs with interface trapped charges including effects of channel mobile charge carriers[J]. J. Semicond., 2017, 38(2): 024004. doi: 10.1088/1674-4926/38/2/024004.
|
Two-dimensional analytical model of double-gate tunnel FETs with interface trapped charges including effects of channel mobile charge carriers
DOI: 10.1088/1674-4926/38/2/024004
More Information
-
Abstract
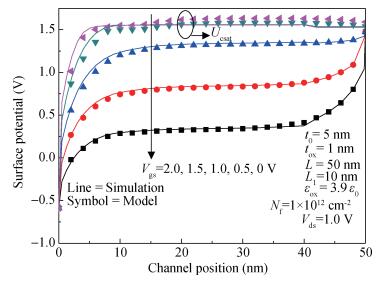
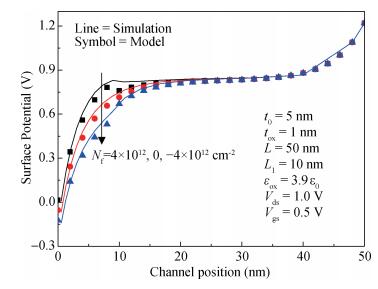
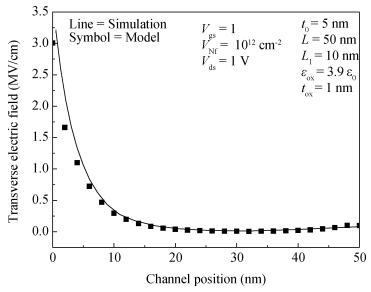
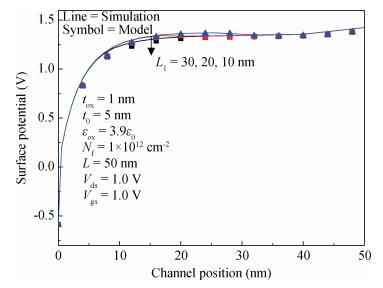
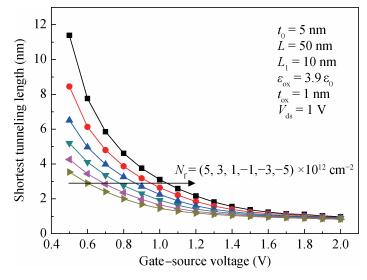
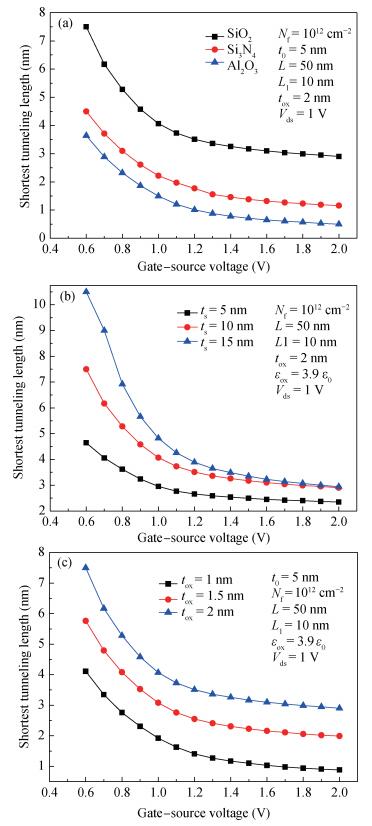
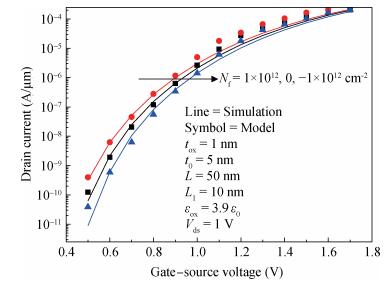
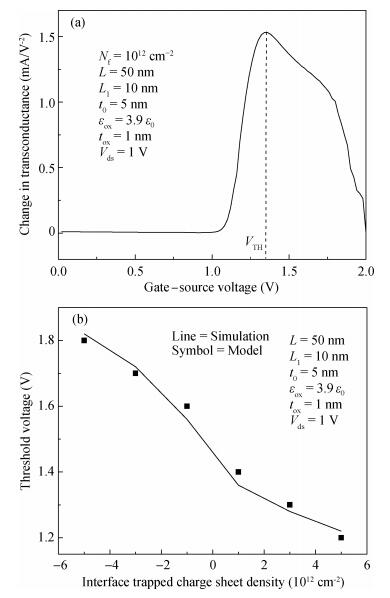
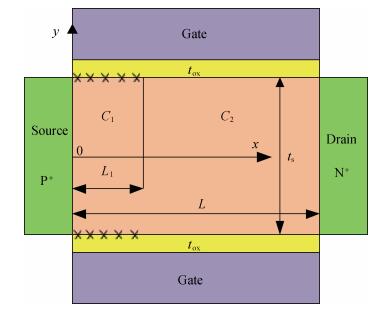
A two-dimensional analytical model of double-gate (DG) tunneling field-effect transistors (TFETs) with interface trapped charges is proposed in this paper. The influence of the channel mobile charges on the potential profile is also taken into account in order to improve the accuracy of the models. On the basis of potential profile, the electric field is derived and the expression for the drain current is obtained by integrating the BTBT generation rate. The model can be used to study the impact of interface trapped charges on the surface potential, the shortest tunneling length, the drain current and the threshold voltage for varying interface trapped charge densities, length of damaged region as well as the structural parameters of the DG TFET and can also be utilized to design the charge trapped memory devices based on TFET. The biggest advantage of this model is that it is more accurate, and in its expression there are no fitting parameters with small calculating amount. Very good agreements for both the potential, drain current and threshold voltage are observed between the model calculations and the simulated results. -
References
[1] Bardon M G, Neves H P, Puers R, et al. Pseudo-two-dimensional model for double-gate tunnel FETs considering the junctions depletion regions. IEEE Trans Electron Devices, 2010, 57(4):827 doi: 10.1109/TED.2010.2040661[2] Shiromani B R, Bahniman G, Bhupesh B. Temperature effect on hetero structure junctionless tunnel FET. J Semicond, 2015, 36(3):034002 doi: 10.1088/1674-4926/36/3/034002[3] Pranav K A. High performance 20 nm GaSb/InAs junctionless tunnel field effect transistor for low power supply. J Semicond, 2015, 36(2):24003 doi: 10.1088/1674-4926/36/2/024003[4] Sivasankaran K, Mallick P S. Impact of parameter fluctuations on RF stability performance of DG tunnel FET. J Semicond, 2015, 36(8):84001 doi: 10.1088/1674-4926/36/8/084001[5] Navjeet B, Subir K S. An analytical model for tunnel barrier modulation in triple metal double gate TFET. IEEE Trans Electron Devices, 2015, 62(7):2136 doi: 10.1109/TED.2015.2434276[6] Verhulst A S, Sorée B, Leonelli D, et al. Modeling the singlegate, double-gate, and gate-all-around tunnel field-effect transistor. Appl Phys Lett, 2007, 91(5):053102 doi: 10.1063/1.2757593[7] Pandey P, Vishnoi R, Kumar M J. A full-range dual material gate tunnel field effect transistor drain current model considering both source and drain depletion region band-to-band tunneling. J Comput Electron, 2015, 14(1):280 doi: 10.1007/s10825-014-0649-x[8] Giovanni B B, Elena G, Antonio G, et al. Dual-metal-gate InAs tunnel FET with enhanced turn-on steepness and high on current. IEEE Trans Electron Devices, 2014, 61(3):776 doi: 10.1109/TED.2014.2298212[9] Hraziia, Andrei V, Amara A, et al. An analysis on the ambipolar current in Si double-gate tunnel FETs. Solid-State Electron, 2012, 70:67 doi: 10.1016/j.sse.2011.11.009[10] Qiu Y X, Wang R S, Huang Q Q, et al. A comparative study on the impacts of interface traps on tunneling FET and MOSFET. IEEE Trans Electron Devices, 2014, 61(5):1284 doi: 10.1109/TED.2014.2312330[11] Huang X Y, Jiao G F, Cao W, et al. Effect of interface traps and oxide charge on drain current degradation in tunneling fieldeffect transistors. IEEE Electron Device Lett, 2010, 31(8):779 doi: 10.1109/LED.2010.2050456[12] Cao W, Yao C J, Jiao G F, et al. Improvement in reliability of tunneling field-effect transistor with p-n-i-n structure. IEEE Trans Electron Devices, 2011, 58(7):2122 doi: 10.1109/TED.2011.2144987[13] Arun Samuel T S, Balamurugan N B. Analytical modeling and simulation of germanium single gate silicon on insulator TFET. J Semicond, 2014, 35(3):034002 doi: 10.1088/1674-4926/35/3/034002[14] Rajat V, Jagadesh K M. Compact analytical model of dual material gate tunneling field-effect transistor using interband tunneling and channel transport. IEEE Trans Electron Devices, 2014, 61(6):1936 doi: 10.1109/TED.2014.2315294[15] Rajat V, Jagadesh K M. 2-D analytical model for the threshold voltage of a tunneling FET with localized charges. IEEE Trans Electron Devices, 2014, 61(9):3054 doi: 10.1109/TED.2014.2332039[16] Xu H F, Dai Y H, Li N, et al. A 2-D semi-analytical model of double-gate tunnel field-effect transistor. J Semicond, 2015, 36(5):054002 doi: 10.1088/1674-4926/36/5/054002[17] Gholizadeh M, Hosseini S E. A 2-D analytical model for doublegate tunnel FETs. IEEE Trans Electron Devices, 2014, 61(5):1494 doi: 10.1109/TED.2014.2313037[18] Narang R, Sasidhar Reddy K V, Saxena M, et al. a dielectricmodulated tunnel-FET-based biosensor for label-free detection:analytical modeling study and sensitivity analysis. IEEE Trans Electron Devices, 2012, 59(10):2809 doi: 10.1109/TED.2012.2208115[19] ATLAS User's Manual. Silvaco Int., Santa Clara, CA, 2009[20] Kao K H, Anne S V, William G V. Direct and indirect band-toband tunneling in germanium-based TFETs. IEEE Trans Electron Devices, 2012, 59(2):292 doi: 10.1109/TED.2011.2175228[21] Hurkx G A M, Klaassen D B M, Knuvers M P G. A new recombination model for device simulation including tunneling. IEEE Trans Electron Devices, 1992, 39(2):331 doi: 10.1109/16.121690[22] Dash S Mishra G P. A 2D analytical cylindrical gate tunnel FET (CG-TFET) model:impact of shortest tunneling distance. Adv Nat Sci:Nanosci Nanotechnol, 2015, 6:035005 doi: 10.1088/2043-6262/6/3/035005[23] Dash S Mishra G P. A new analytical threshold voltage model of cylindrical gate tunnel FET (CG-TFET). Superlattices Microstruct, 2015, 86:211 doi: 10.1016/j.spmi.2015.07.049[24] Tura A, Zhang Z N, Liu P C, et al. Vertical silicon p-n-p-n tunnel nMOSFET with MBE-grown tunneling junction. IEEE Trans Electron Devices, 2011, 58(7):1907 doi: 10.1109/TED.2011.2148118 -
Proportional views





 DownLoad:
DownLoad: