| Citation: |
Soumaia Djaadi, Kamal Eddine Aiadi, Sofiane Mahtout. First principles study of structural, electronic and magnetic properties of SnGen(0, ±1) (n = 1–17) clusters[J]. Journal of Semiconductors, 2018, 39(4): 042001. doi: 10.1088/1674-4926/39/4/042001
****
S Djaadi, K E Aiadi, S Mahtout. First principles study of structural, electronic and magnetic properties of SnGen(0, ±1) (n = 1–17) clusters[J]. J. Semicond., 2018, 39(4): 042001. doi: 10.1088/1674-4926/39/4/042001.
|
First principles study of structural, electronic and magnetic properties of SnGen(0, ±1) (n = 1–17) clusters
DOI: 10.1088/1674-4926/39/4/042001
More Information
-
Abstract
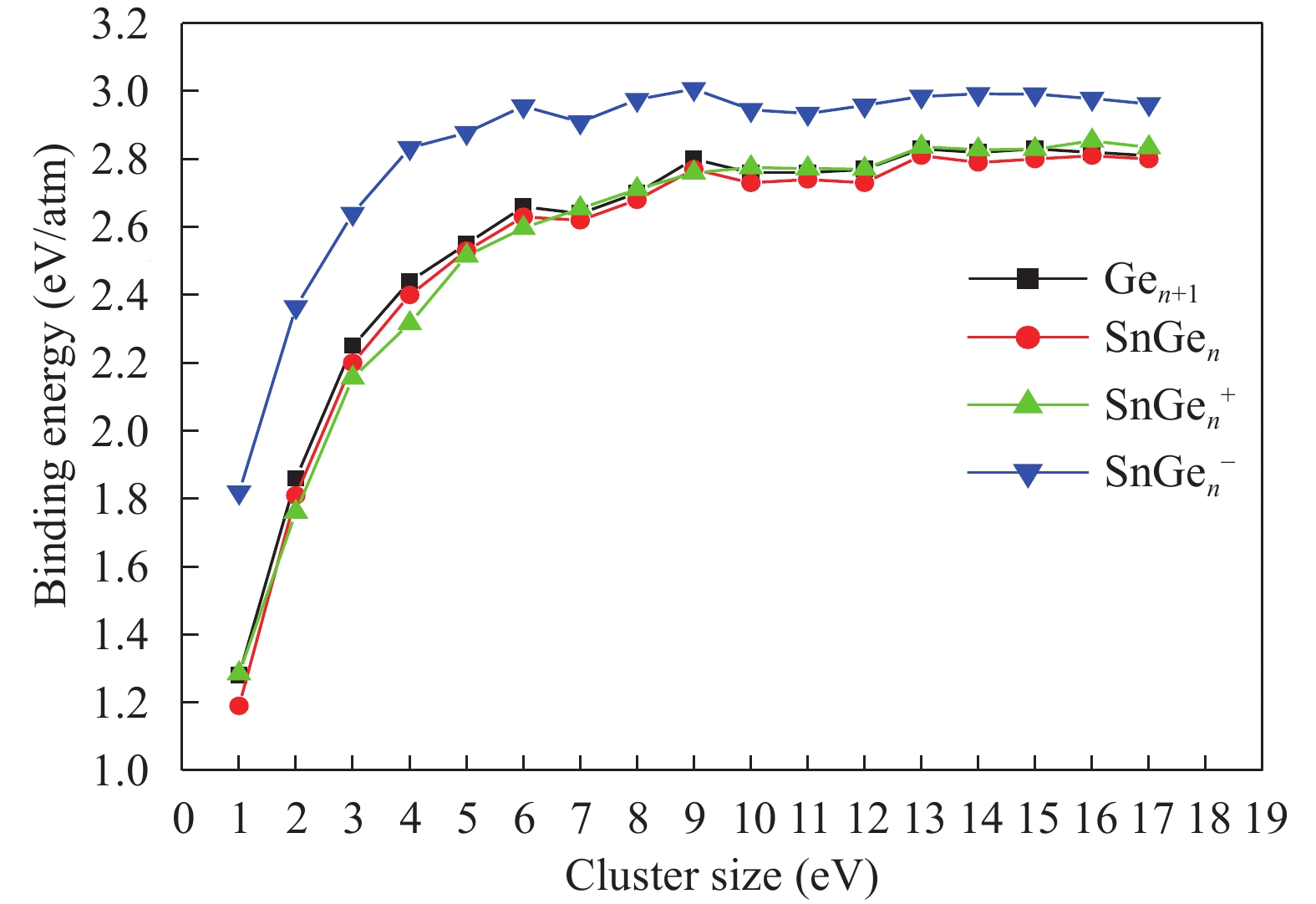
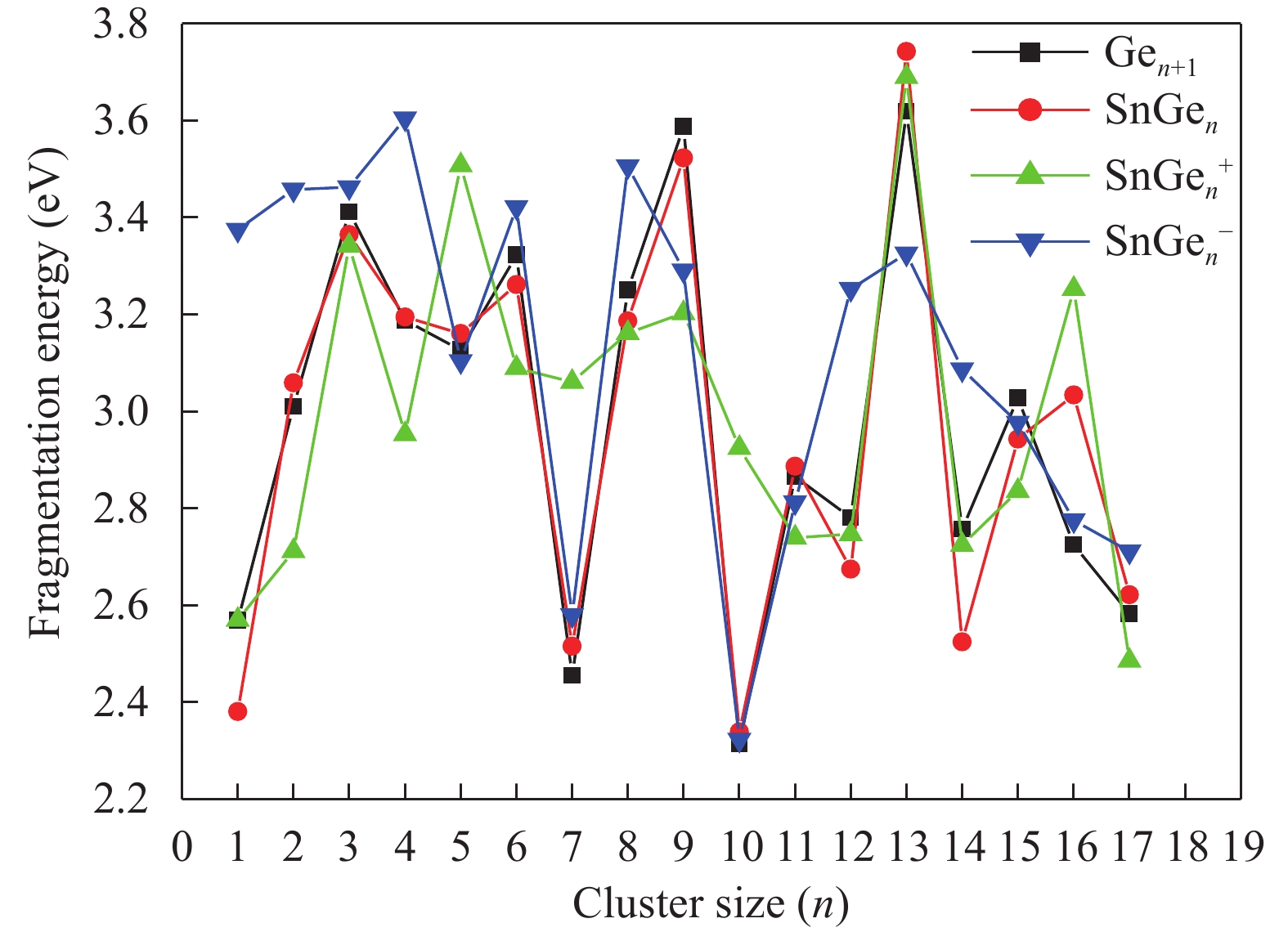
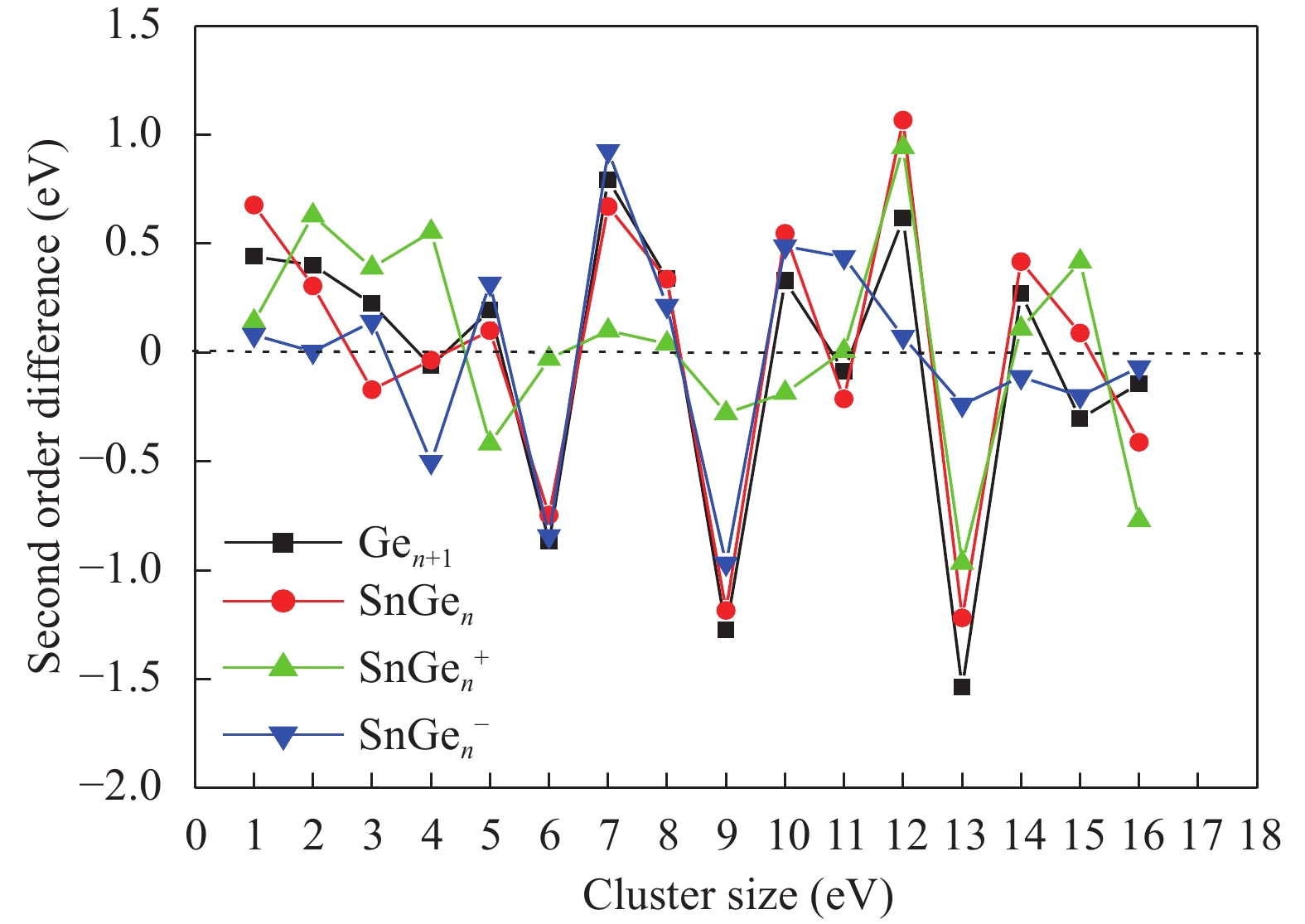
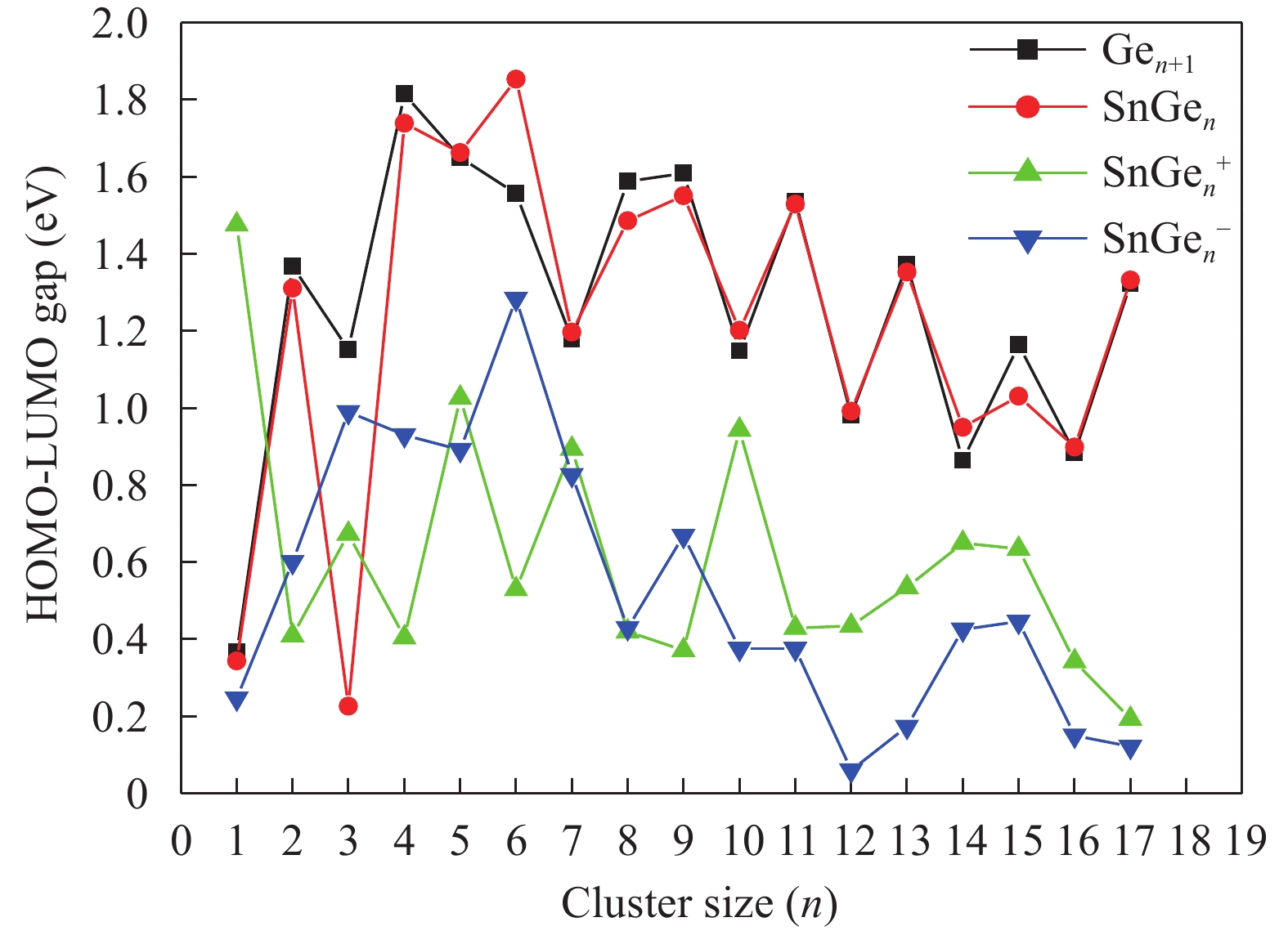
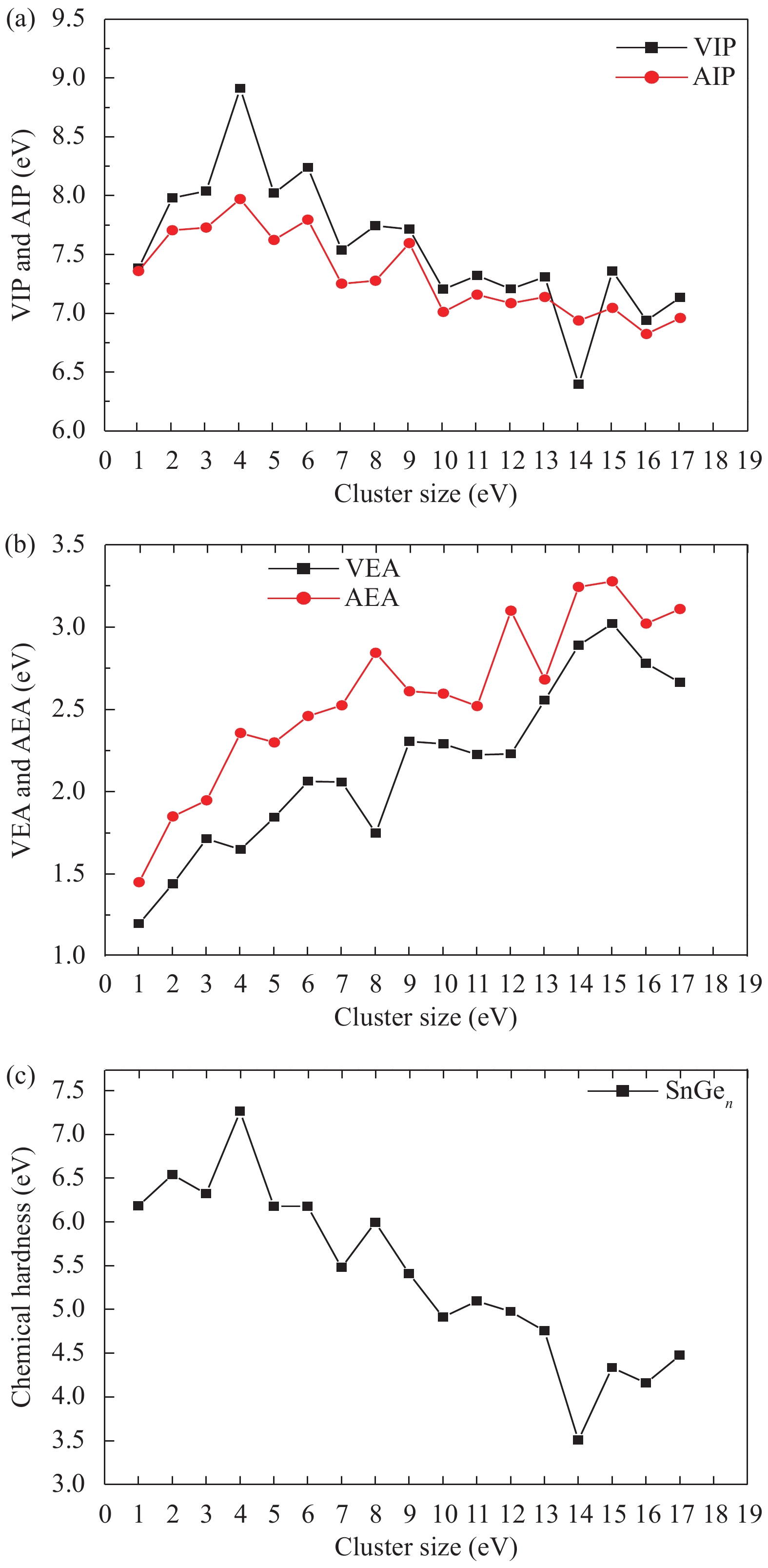
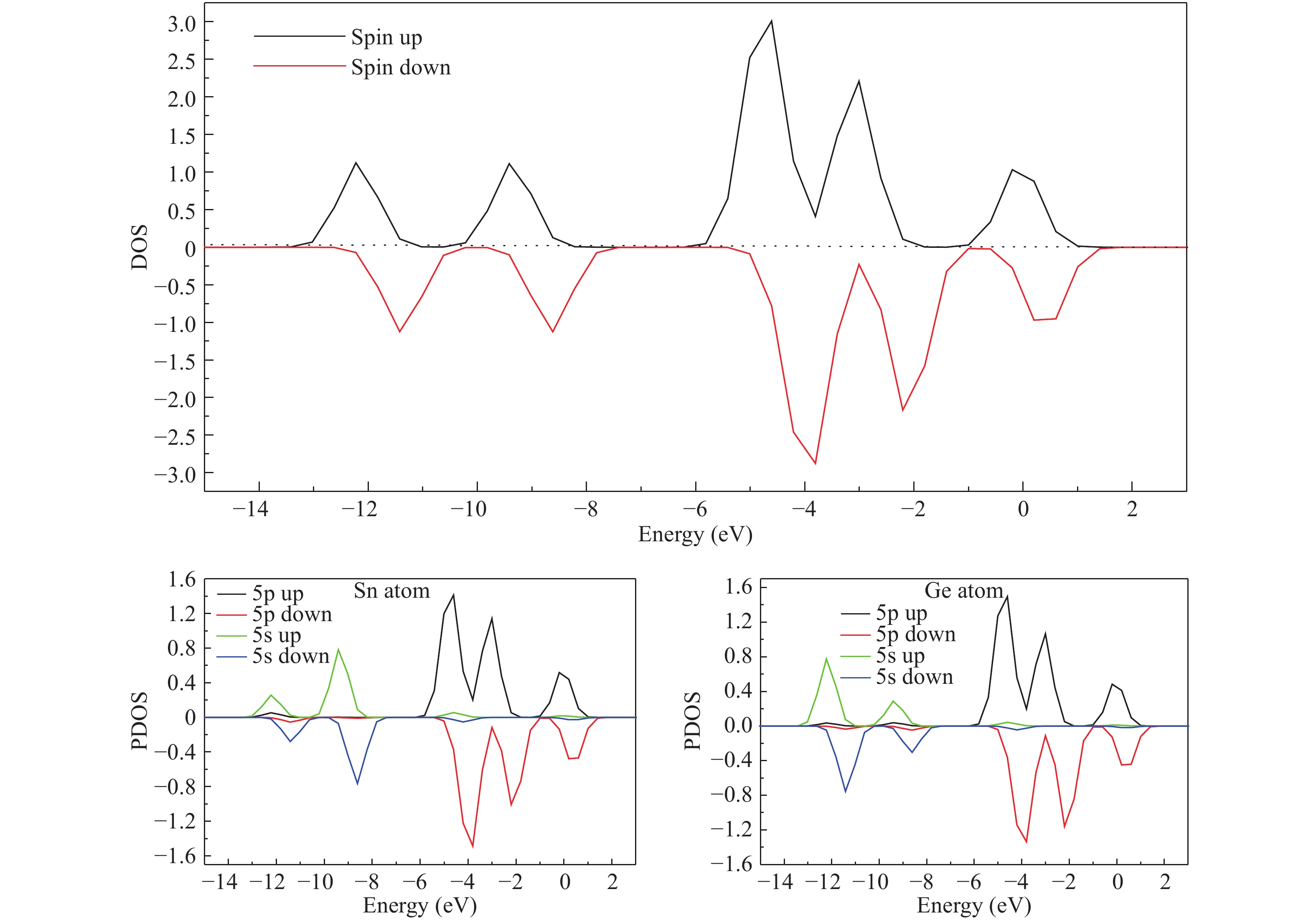
The structures, relative stability and magnetic properties of pure Gen+1, neutral cationic and anionic SnGen (n = 1–17) clusters have been investigated by using the first principles density functional theory implemented in SIESTA packages. We find that with the increasing of cluster size, the Gen+1 and SnGen(0, ±1) clusters tend to adopt compact structures. It has been also found that the Sn atom occupied a peripheral position for SnGen clusters when n < 12 and occupied a core position for n > 12. The structural and electronic properties such as optimized geometries, fragmentation energy, binding energy per atom, HOMO–LUMO gaps and second-order differences in energy of the pure Ge n+1 and SnGen clusters in their ground state are calculated and analyzed. All isomers of neutral SnGen clusters are generally nonmagnetic except for n = 1 and 4, where the total spin magnetic moments is 2μb. The total (DOS) and partial density of states of these clusters have been calculated to understand the origin of peculiar magnetic properties. The cluster size dependence of vertical ionization potentials, vertical electronic affinities, chemical hardness, adiabatic electron affinities and adiabatic ionization potentials have been calculated and discussed. -
References
[1] Samanta P N, Das K K. Electronic structure, bonding, and properties of SnmGen (m + n ≤ 5) clusters: a DFT study. Comput Theor Chem, 2012, 980: 123 doi: 10.1016/j.comptc.2011.11.038[2] Mahtout S, Tariket Y. Electronic and magnetic properties of CrGen (15 ≤ n ≤ 29) clusters: a DFT study. Chem Phys, 2016, 472: 270 doi: 10.1016/j.chemphys.2016.03.011[3] Shvartsburg A A, Liu B, Lu Z Y, et al. Structures of germanium clusters: where the growth patterns of silicon and germanium clusters diverge. Phys Rev Lett, 1999, 83(11): 2167 doi: 10.1103/PhysRevLett.83.2167[4] Burton G R, Xu C, Arnold C C, et al. Photoelectron spectroscopy and zero electron kinetic energy spectroscopy of germanium cluster anions. J Chem Phys, 1996, 104(8): 2757 doi: 10.1063/1.471098[5] Burton G R, Xu C, Neumark D M. study of small semiconductor clusters using anion photoelectron spectroscopy: germanium clusters (Gen, n = 2−15). Surf Rev Lett, 1996, 03(01): 383[6] Negishi Y, Kawamata H, Hayakawa F, et al. The infrared HOMO–LUMO gap of germanium clusters. Chem Phys Lett, 1998, 294(4): 370[7] Gingerich K A, Schmude Jr R, Baba M S, et al. Atomization enthalpies and enthalpies of formation of the germanium clusters, Ge 5, Ge 6, Ge 7, and Ge 8 by Knudsen effusion mass spectrometry. J Chem Phys, 2000, 112(17): 7443 doi: 10.1063/1.481343[8] Hostutler D A, Li H, Clouthier D J, et al. Exploring the Bermuda triangle of homonuclear diatomic spectroscopy: the electronic spectrum and structure of Ge2. J Chem Phys, 2002, 116(10): 4135 doi: 10.1063/1.1431281[9] Bals S, Aert S Van, Romero C, et al. Atomic scale dynamics of ultrasmall germanium clusters. Nat Commun, 2012, 3: 897 doi: 10.1038/ncomms1887[10] Haeck J De, Tai T B, Bhattacharyya S, et al. Structures and ionization energies of small lithium doped germanium clusters. PCCP, 2013, 15(14): 5151 doi: 10.1039/c3cp44395g[11] Deutsch P, Curtiss L, Blaudeau J P. Electron affinities of germanium anion clusters, Gen (n = 2–5). Chem Phys Lett, 2001, 344(1): 101 doi: 10.1016/S0009-2614(01)00734-5[12] Wang J, Wang G, Zhao J. Structure and electronic properties of Gen (n = 2–25) clusters from density-functional theory. Phys Rev B, 2001, 64(20): 205411 doi: 10.1103/PhysRevB.64.205411[13] Wang J, Yang M, Wang G, et al. Dipole polarizabilities of germanium clusters. Chem Phys Lett, 2003, 367(3): 448[14] Kikuchi H, Takahashi M, Kawazoe Y. Theoretical investigation of stable structures of Ge6 clusters with various negative charges. Mater Trans-JIM, 2006, 47(11): 2624 doi: 10.2320/matertrans.47.2624[15] Ma S, Wang G. Structures of medium size germanium clusters. J Mol Struct: THEOCHEM, 2006, 767(1): 75[16] Zhao W J, Wang Y X. Geometries, stabilities, and magnetic properties of MnGen (n = 2–16) clusters: density-functional theory investigations. J Mol Struct: THEOCHEM, 2009, 901(1): 18[17] Li X J, Ren H J, Yang L M. An investigation of electronic structure and aromaticity in medium-sized nanoclusters of gold-doped germanium. J Nanomater, 2012, 2012: 3[18] Zhao W J, Wang Y X. Geometries, stabilities, and electronic properties of FeGen (n = 9–16) clusters: density-functional theory investigations. Chem Phys, 2008, 352(1): 291[19] Shi S, Liu Y, Zhang C, et al. A computational investigation of aluminum-doped germanium clusters by density functional theory study. Comput Theor Chem, 2015, 1054: 8 doi: 10.1016/j.comptc.2014.12.004[20] Li X, Su K, Yang X, et al. Size-selective effects in the geometry and electronic property of bimetallic Au–Ge nanoclusters. Comput Theor Chem, 2013, 1010: 32 doi: 10.1016/j.comptc.2013.01.012[21] Kapila N, Jindal V, Sharma H. Structural, electronic and magnetic properties of Mn, Co, Ni in Gen for (n = 1–13). Physica B, 2011, 406(24): 4612[22] Tang C, Liu M, Zhu W, et al. Probing the geometric, optical, and magnetic properties of 3d transition-metal endohedral Ge 12 M (M = Sc–Ni) clusters. Comput Theor Chem, 2011, 969(1): 56[23] Katırcıoğlu Ş. Structure and stability of GenCm−n clusters. J Mol Struct: THEOCHEM, 2003, 629(1): 295[24] Andzelm J, Russo N, Salahub D R. Ground and excited states of group IVA diatomics from local‐spin‐density calculations: model potentials for Si, Ge, and Sn. J Chem Phys, 1987, 87(11): 6562 doi: 10.1063/1.453441[25] Schmude Jr R W, Gingerich K A. Thermodynamic investigation of small germanium–tin clusters with a mass spectrometer. J Chem Phys, 1998, 109(8): 3069 doi: 10.1063/1.476898[26] Han J G, Zhang P F, Li Q X, et al. A theoretical investigation of GenSn (n = 1–4) clusters. J Mol Struct: THEOCHEM, 2003, 624(1): 257[27] Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev, 1964, 136(3B): B864 doi: 10.1103/PhysRev.136.B864[28] Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects. Phys Rev, 1965, 140(4A): A1133 doi: 10.1103/PhysRev.140.A1133[29] Ordejón P, Artacho E, Soler J M. Self-consistent order-N density-functional calculations for very large systems. Phys Rev B, 1996, 53(16): R10441 doi: 10.1103/PhysRevB.53.R10441[30] Perdew J P, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B, 1981, 23(10): 5048 doi: 10.1103/PhysRevB.23.5048[31] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77(18): 3865 doi: 10.1103/PhysRevLett.77.3865[32] Kleinman L, Bylander D. Efficacious form for model pseudopotentials. Phys Rev Lett, 1982, 48(20): 1425 doi: 10.1103/PhysRevLett.48.1425[33] Troullier N, Martins J L. Efficient pseudopotentials for plane-wave calculations. Phys Rev B, 1991, 43(3): 1993 doi: 10.1103/PhysRevB.43.1993[34] Kapila N, Garg I, Jindal V, et al. First principle investigation into structural growth and magnetic properties in GenCr clusters for n = 1–13. J Magn Magn Mate, 2012, 324(18): 2885[35] Sosa-Hernández E, Alvarado-Leyva P. Magnetic properties of stable structures of small binary FenGem (n + m ≤ 4) clusters. Physica E, 2009, 42(1): 17 doi: 10.1016/j.physe.2009.07.013[36] Wang J, Han J G. A computational investigation of copper-doped germanium and germanium clusters by the density-functional theory. J Chem Phys, 2005, 123(24): 244303 doi: 10.1063/1.2148949[37] Hou X J, Gopakumar G, Lievens P, et al. Chromium-doped germanium clusters CrGen (n = 1−5): geometry, electronic structure, and topology of chemical bonding. J Phys Chem A, 2007, 111(51): 13544[38] Menon M. A transferable nonorthogonal tight-binding scheme for germanium. J Phys: Condens Matter, 1998, 10(48): 10991 doi: 10.1088/0953-8984/10/48/019[39] Li S D, Zhao G Z, Wu H S, et al. Ionization potentials, electron affinities, and vibrational frequencies of Gen (n = 5–10) neutrals and charged ions from density functional theory. J Chem Phys, 2001, 115(20): 9255[40] Kant A, Strauss B H. Atomization energies of the polymers of germanium, Ge2 to Ge7. J Chem Phys, 1966, 45(3): 822 doi: 10.1063/1.1727688[41] Vasiliev I, Öğüt S, Chelikowsky J R. Ab initio calculations for the polarizabilities of small semiconductor clusters. Phys Rev Lett, 1997, 78(25): 4805 doi: 10.1103/PhysRevLett.78.4805[42] Wang J, Han J G. The growth behaviors of the Zn-doped different sized germanium clusters: a density functional investigation. Chem Phys, 2007, 342(1): 253[43] Parr R G, Pearson R G. Absolute hardness: companion parameter to absolute electronegativity. J Am Chem Soc, 1983, 105(26): 7512 doi: 10.1021/ja00364a005[44] Parr R, Yang W. Density functional methods of atoms and molecules. New York: Oxford University Press, 1989 -
Proportional views






 DownLoad:
DownLoad: