| Citation: |
Shuang Yu, Yi Peng, Guoqiang Zhao, Jianfa Zhao, Xiancheng Wang, Jun Zhang, Zheng Deng, Changqing Jin. Colossal negative magnetoresistance in spin glass Na(Zn,Mn)Sb[J]. Journal of Semiconductors, 2023, 44(3): 032501. doi: 10.1088/1674-4926/44/3/032501
****
S Yu, Y Peng, G Q Zhao, J F Zhao, X C Wang, J Zhang, Z Deng, C Q Jin. Colossal negative magnetoresistance in spin glass Na(Zn,Mn)Sb[J]. J. Semicond, 2023, 44(3): 032501. doi: 10.1088/1674-4926/44/3/032501
|
Colossal negative magnetoresistance in spin glass Na(Zn,Mn)Sb
DOI: 10.1088/1674-4926/44/3/032501
More Information
-
Abstract
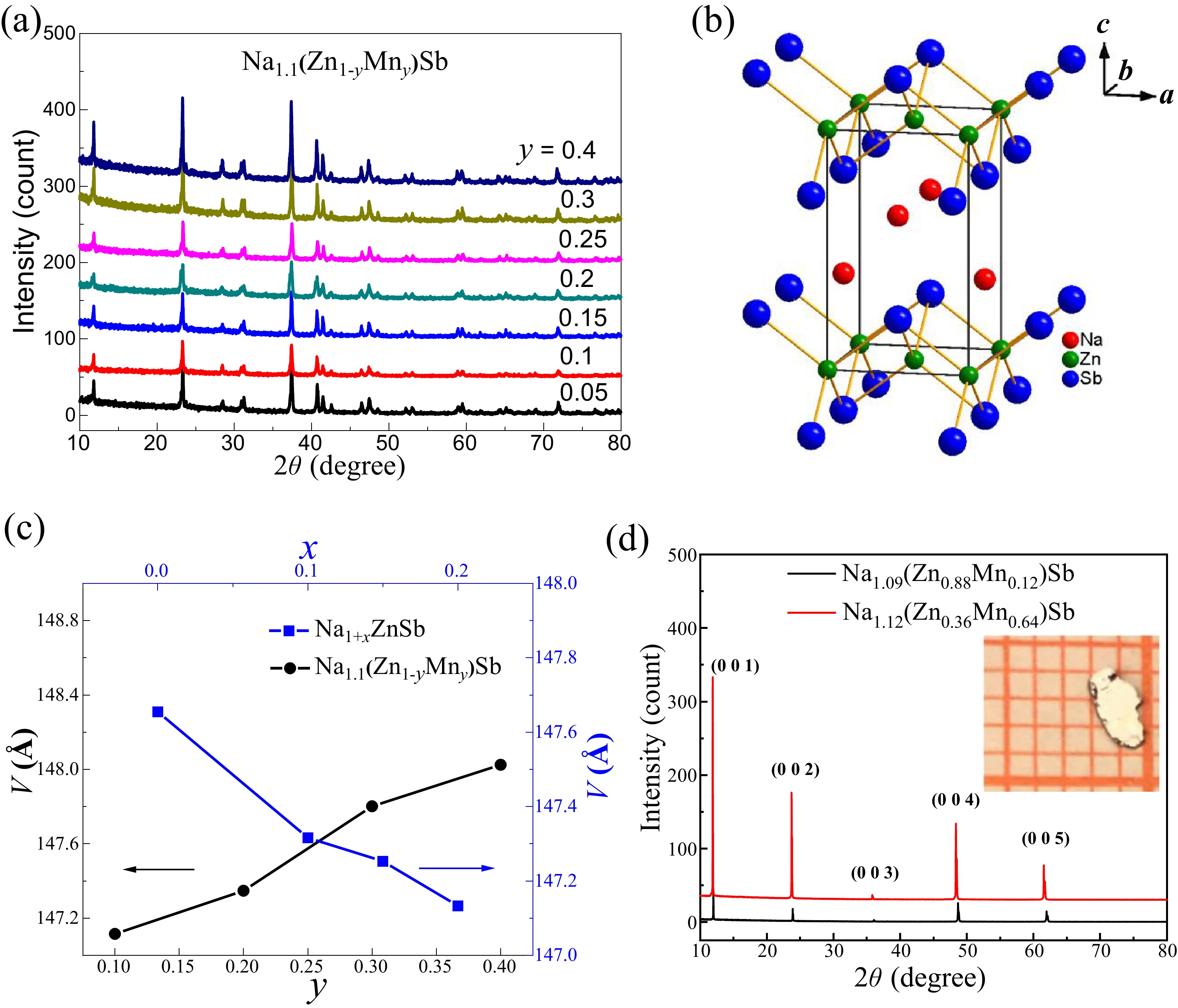
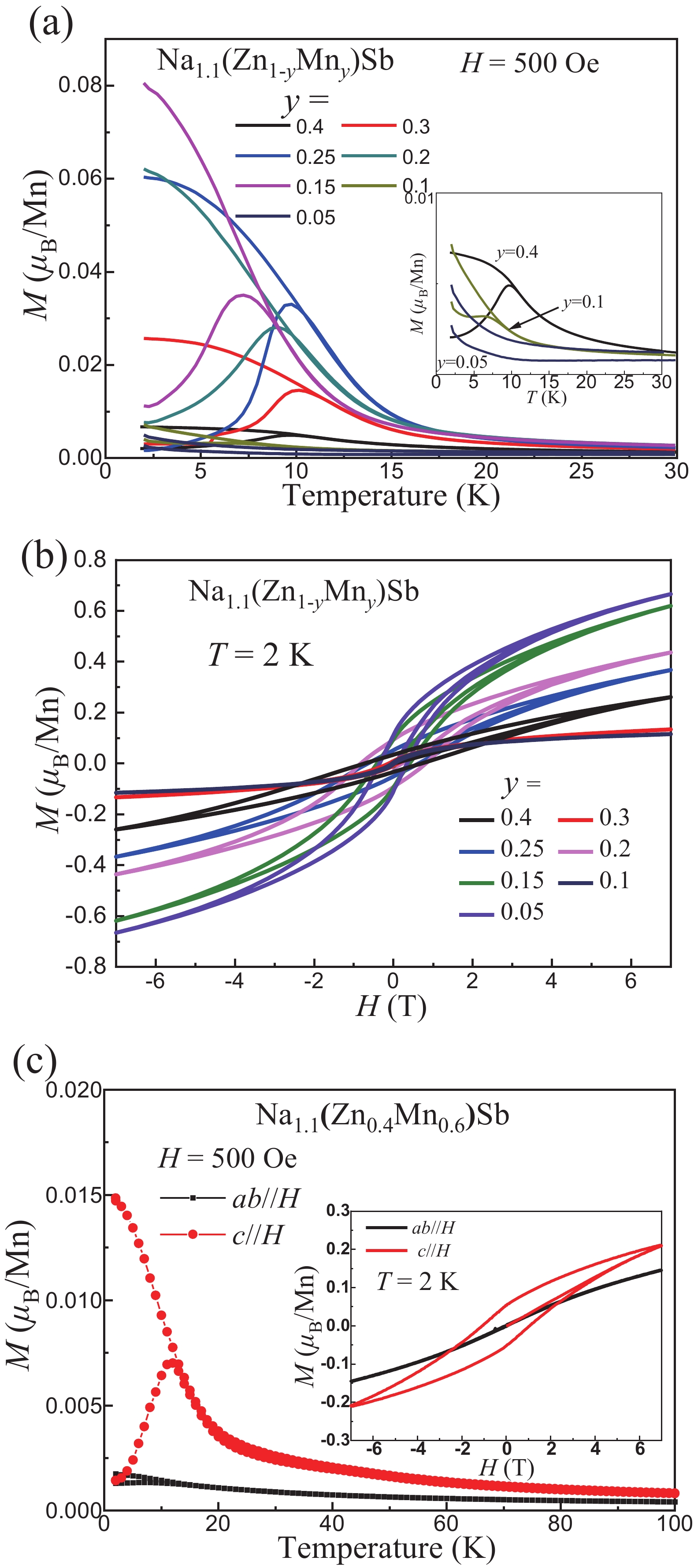
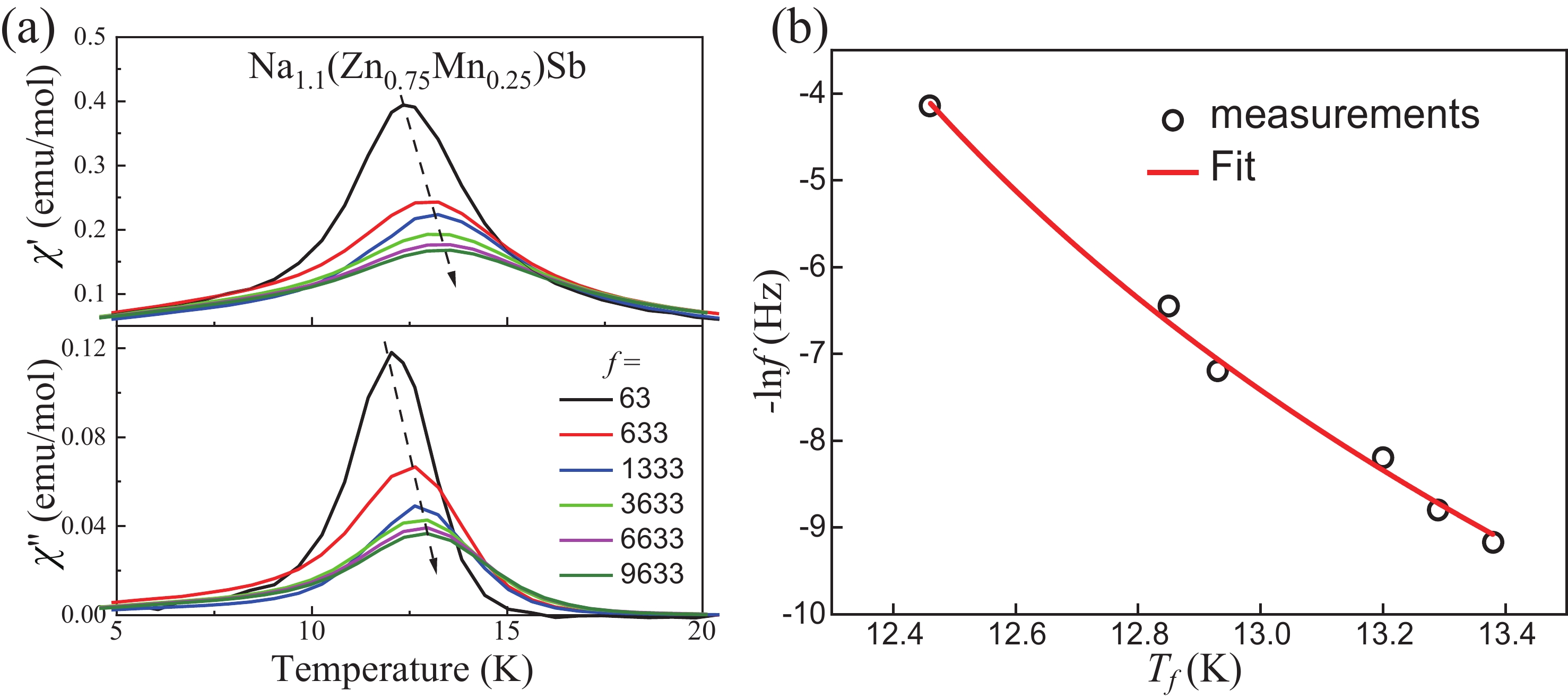
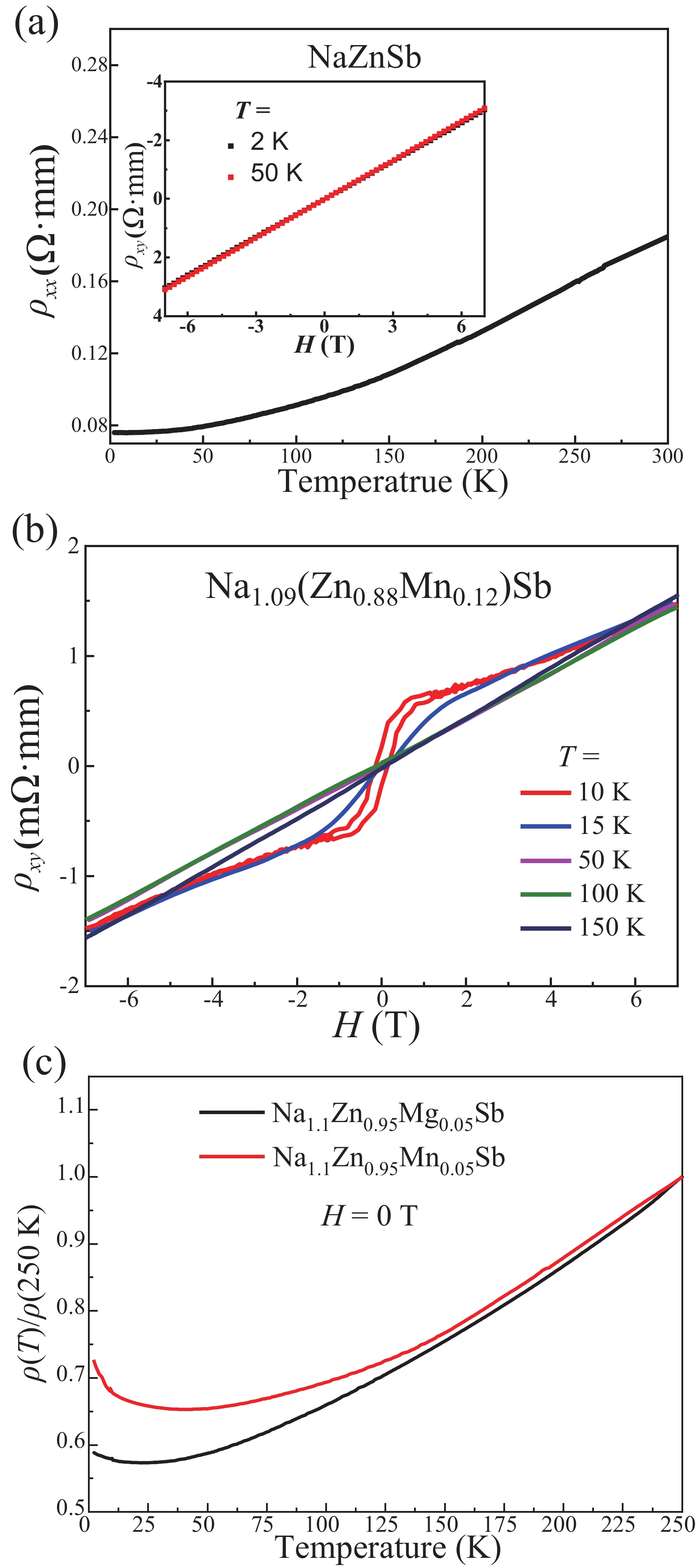
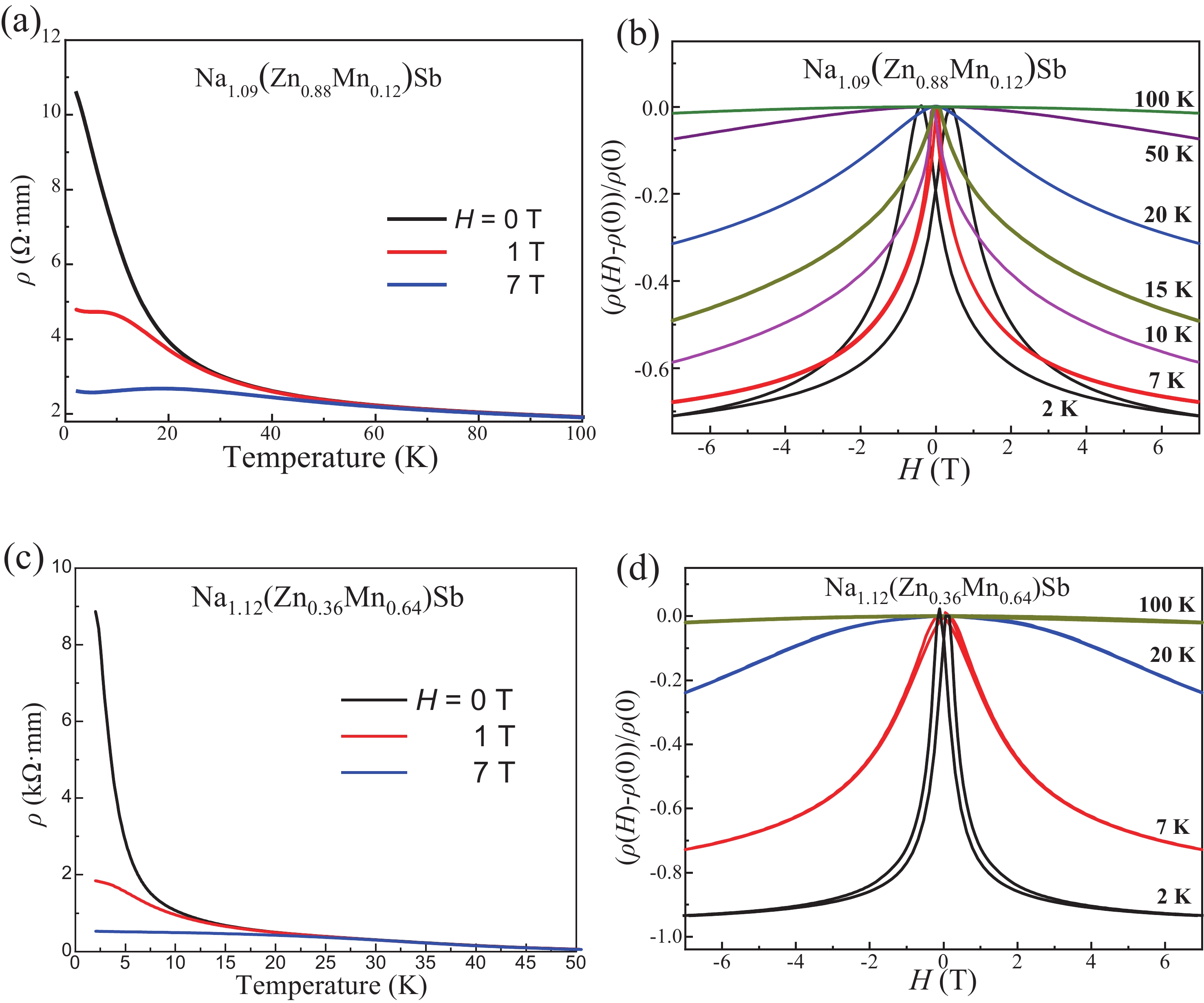
We report the study of magnetic and transport properties of polycrystalline and single crystal Na(Zn,Mn)Sb, a new member of “111” type of diluted magnetic materials. The material crystallizes into Cu2Sb-type structure which is isostructural to “111” type Fe-based superconductors. With suitable carrier and spin doping, the Na(Zn,Mn)Sb establishes spin-glass ordering with freezing temperature (Tf) below 15 K. Despite lack of long-range ferromagnetic ordering, Na(Zn,Mn)Sb single crystal still shows sizeable anomalous Hall effect below Tf. Carrier concentration determined by Hall effect measurements is over 1019 cm–3. More significantly, we observe colossal negative magnetoresistance (MR ≡ [ρ(H) − ρ(0)]/ρ(0)) of –94% in the single crystal sample. -
References
[1] Žutić I, Fabian J, Das Sarma S. Spintronics: Fundamentals and applications. Rev Mod Phys, 2004, 76, 323 doi: 10.1103/RevModPhys.76.323[2] Dietl T, Ohno H, Matsukura F, et al. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science, 2000, 287, 1019 doi: 10.1126/science.287.5455.1019[3] Dietl T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat Mater, 2010, 9, 965 doi: 10.1038/nmat2898[4] Hirohata A, Sukegawa H, Yanagihara H, et al. Roadmap for emerging materials for spintronic device applications. IEEE Trans Magn, 2015, 51, 1 doi: 10.1109/TMAG.2015.2457393[5] Song L, Yan W, Wang H L, et al. Resonant enhancement of magnetic damping driven by coherent acoustic phonons in thin Co2FeAl film epitaxied on GaAs. J Semicond, 2021, 42, 032501 doi: 10.1088/1674-4926/42/3/032501[6] von Molnár S. Magnetotransport in magnetic semiconductors and possible applications. Sens Actuat A, 2001, 91, 161 doi: 10.1016/S0924-4247(01)00466-6[7] Nigam A K, Majumdar A K. Magnetoresistance in canonical spin-glasses. Phys Rev B, 1983, 27, 495 doi: 10.1103/PhysRevB.27.495[8] Furdyna J K. Diluted magnetic semiconductors. J Appl Phys, 1988, 64, R29 doi: 10.1063/1.341700[9] Paalanen M A, Bhatt R N. Transport and thermodynamic properties across the metal-insulator transition. Phys B, 1991, 169, 223 doi: 10.1016/0921-4526(91)90233-5[10] Deng Z, Jin C Q, Liu Q Q, et al. Li(Zn, Mn)As as a new generation ferromagnet based on a I–II–V semiconductor. Nat Commun, 2011, 2, 422 doi: 10.1038/ncomms1425[11] Zhao K, Deng Z, Wang X C, et al. New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the ‘122’ iron-based superconductors. Nat Commun, 2013, 4, 1442 doi: 10.1038/ncomms2447[12] Zhao G Q, Deng Z, Jin C Q. Advances in new generation diluted magnetic semiconductors with independent spin and charge doping. J Semicond, 2019, 40, 081505 doi: 10.1088/1674-4926/40/8/081505[13] Zhao G Q, Lin C J, Deng Z, et al. Single crystal growth and spin polarization measurements of diluted magnetic semiconductor (BaK)(ZnMn)2As2. Sci Rep, 2017, 7, 14473 doi: 10.1038/s41598-017-08394-z[14] Zhao X, Dong J, Fu L, et al. (Ba1−xNax)F(Zn1−xMnx)Sb: A novel fluoride-antimonide magnetic semiconductor with decoupled charge and spin doping. J Semicond, 2022, 43, 112501 doi: 10.1088/1674-4926/43/11/112501[15] Dong J, Zhao X Q, Fu L C, et al. (Ca, K)(Zn, Mn)2As2: Ferromagnetic semiconductor induced by decoupled charge and spin doping in CaZn2As2. J Semicond, 2022, 43, 072501 doi: 10.1088/1674-4926/43/7/072501[16] Zhao K, Chen B J, Zhao G Q, et al. Ferromagnetism at 230 K in (Ba0.7K0.3)(Zn0.85Mn0.15)2As2 diluted magnetic semiconductor. Chin Sci Bull, 2014, 59, 2524 doi: 10.1007/s11434-014-0398-z[17] Yang X J, Chen Q, Li Y P, et al. Sr0.9K0.1Zn1.8Mn0.2As2: A ferromagnetic semiconductor with colossal magnetoresistance. EPL Europhys Lett, 2014, 107, 67007 doi: 10.1209/0295-5075/107/67007[18] Yang X J, Li Y K, Zhang P, et al. K and Mn co-doped BaCd2As2: A hexagonal structured bulk diluted magnetic semiconductor with large magnetoresistance. J Appl Phys, 2013, 114, 223905 doi: 10.1063/1.4842875[19] Suzuki H, Zhao K, Shibata G, et al. Photoemission and X-ray absorption studies of the isostructural to Fe-based superconductors diluted magnetic semiconductor Ba1−xKx(Zn1−yMny)2As2. Phys Rev B, 2015, 91, 140401 doi: 10.1103/PhysRevB.91.140401[20] Frandsen B A, Gong Z Z, Terban M W, et al. Local atomic and magnetic structure of dilute magnetic semiconductor (Ba, K)(Zn, Mn)2As2. Phys Rev B, 2016, 94, 094102 doi: 10.1103/PhysRevB.94.094102[21] Glasbrenner J K, Žutić I, Mazin I I. Theory of Mn-doped II-II-V semiconductors. Phys Rev B, 2014, 90, 140403 doi: 10.1103/PhysRevB.90.140403[22] Žutić I, Zhou T. Tailoring magnetism in semiconductors. Sci China Phys Mech Astron, 2018, 61, 067031 doi: 10.1007/s11433-018-9191-0[23] Wang X C, Liu Q Q, Lv Y X, et al. The superconductivity at 18 K in LiFeAs system. Solid State Commun, 2008, 148, 538 doi: 10.1016/j.ssc.2008.09.057[24] Wang R, Huang Z X, Zhao G Q, et al. Out-of-plane easy-axis in thin films of diluted magnetic semiconductor Ba1−xKx(Zn1−yMny)2As2. AIP Adv, 2017, 7, 045017 doi: 10.1063/1.4982713[25] Deng Z, Zhao K, Gu B, et al. Diluted ferromagnetic semiconductor Li(Zn, Mn)P with decoupled charge and spin doping. Phys Rev B, 2013, 88, 081203 doi: 10.1103/PhysRevB.88.081203[26] Jaiganesh G, Merita Anto Britto T, Eithiraj R D, et al. Electronic and structural properties of NaZnX (X = P, As, Sb): An ab initio study. J Phys: Condens Matter, 2008, 20, 085220 doi: 10.1088/0953-8984/20/8/085220[27] Toby B H. EXPGUI, a graphical user interface for GSAS. J Appl Cryst, 2001, 34, 210 doi: 10.1107/S0021889801002242[28] Deng Z, Retuerto M, Liu S Z, et al. Dynamic ferrimagnetic order in a highly distorted double perovskite Y2CoRuO6. Chem Mater, 2018, 30, 7047 doi: 10.1021/acs.chemmater.8b02728[29] Dho J, Kim W S, Hur N H. Reentrant spin glass behavior in Cr-doped perovskite manganite. Phys Rev Lett, 2002, 89, 027202 doi: 10.1103/PhysRevLett.89.027202[30] Kilanski L, Szymczak R, Dobrowolski W, et al. Negative magnetoresistance and anomalous Hall effect in GeMnTe-SnMnTe spin-glass-like system. J Appl Phys, 2013, 113, 063702 doi: 10.1063/1.4790321[31] Sinova J, Jungwirth T, Černe J. Magneto-transport and magneto-optical properties of ferromagnetic (III, Mn)V semiconductors: A review. Int J Mod Phys B, 2004, 18, 1083 doi: 10.1142/S0217979204024677[32] Liu X, Riney L, Guerra J, et al. Colossal negative magnetoresistance from hopping in insulating ferromagnetic semiconductors. J Semicond, 2022, 43, 112502 doi: 10.1088/1674-4926/43/11/112502 -
Proportional views





 DownLoad:
DownLoad:










 Shuang Yu:received her Ph.D. degree from Institute of Physics, Chinese Academy of Sciences in 2020. Since 2015, she has been working in Prof. Changqing Jin's group under the supervision of Associate Professor Zheng Deng and Professor Changqing Jin, with research focusing on magnetic semiconductors. Now she works in Intel Company at Dalian
Shuang Yu:received her Ph.D. degree from Institute of Physics, Chinese Academy of Sciences in 2020. Since 2015, she has been working in Prof. Changqing Jin's group under the supervision of Associate Professor Zheng Deng and Professor Changqing Jin, with research focusing on magnetic semiconductors. Now she works in Intel Company at Dalian Zheng Deng:received his Ph.D. degree from Institute of Physics, Chinese Academy of Sciences in 2012. He worked as a postdoc in the Department of Chemistry in Rutgers University from 2013.1 to 2015.1. Since then, he has been working as an associate professor at IOPCAS. His research interests include magnetic semiconductors, superconductors and emergent materials under extreme conditions
Zheng Deng:received his Ph.D. degree from Institute of Physics, Chinese Academy of Sciences in 2012. He worked as a postdoc in the Department of Chemistry in Rutgers University from 2013.1 to 2015.1. Since then, he has been working as an associate professor at IOPCAS. His research interests include magnetic semiconductors, superconductors and emergent materials under extreme conditions Changqing Jin:is currently a professor at Institute of Physics, Chinese Academy of Sciences. He received his Ph.D. degree from IOPCAS in 1991. He is a fellow of American Physical Society, a fellow of American Association for the Advancement of Science, and a fellow of the Institute of Physics (UK). His research group focuses on new Quantum matters by design using extreme conditions, and effects of pressures on novel emergent phenomena
Changqing Jin:is currently a professor at Institute of Physics, Chinese Academy of Sciences. He received his Ph.D. degree from IOPCAS in 1991. He is a fellow of American Physical Society, a fellow of American Association for the Advancement of Science, and a fellow of the Institute of Physics (UK). His research group focuses on new Quantum matters by design using extreme conditions, and effects of pressures on novel emergent phenomena



