1. Introduction

The double-gate metal oxide semiconductor field-effect transistor (DG MOSFET) architecture is considered as a promising device for nanoscale CMOS-based application. It has attracted the attention of a wide range of researchers, and this has led to many enhancements at both the design and practical implementation levels, where new materials and structural improvements have been adopted in order to obtain a higher efficiency performance^[1-3].

However, even with all these efforts, many of the proposed improvements will be put into doubt if the severe constraints imposed by the current trends in downscaling and high packaging of electronics components are not treated appropriately^[4]. In fact, by reducing the channel length of the device, its performance is affected, and such correlation is known as the short channel effect (SCE). The situation becomes worse when reaching the sub-100 nm technology node, where SCEs are aggressively amplified and various device characteristics are degraded considerably^[5]. In addition, with the continuous scaling of the geometrical dimensions of MOSFET devices, their accurate modeling under various conditions of the working regime is becoming not only a critical domain, but also a necessary subject for understanding the miniaturization limits. The analytical modeling that has succeeded in some simple situations is in this case an intractable task due to the many mathematical and computational drawbacks encountered, especially when manipulating the joint Schrödinger/Poisson equation.

Another reliability drawback that is basically related to the reduction in the device dimensions is the formation of interface traps under the hot-carrier injection effect^[6]. The hot-carrier-induced damage in MOSFET devices has two harmful consequences: trapping of carriers on the defect sites in the oxide region, and the creation of interface traps at the silicon-oxide interface^[7]. As a result, the most obvious incident of this ageing phenomenon is that various parameters of the device become dependent on the duration of the work. For this reason, the carrier trapping in gate oxides is considered as the principal cause of instability for short channel MOSFETs, and has become one of the most important concerns for future MOS-integrated circuit development.

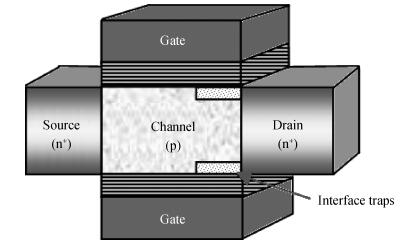
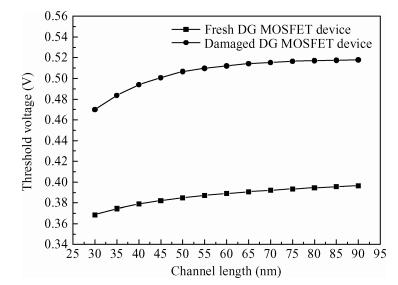
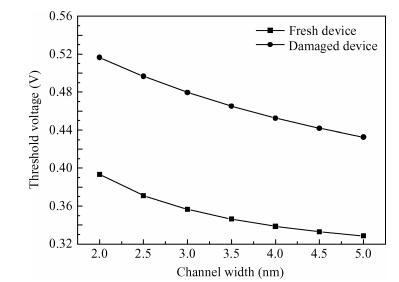
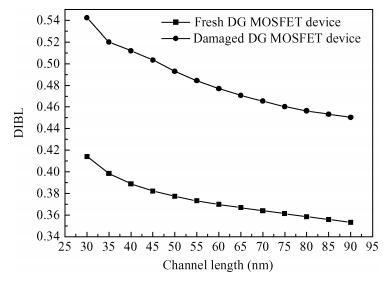
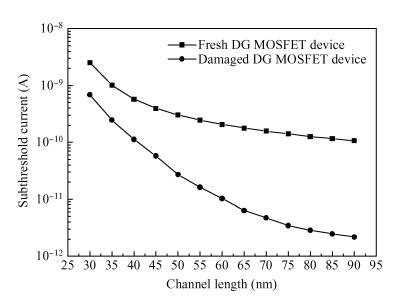
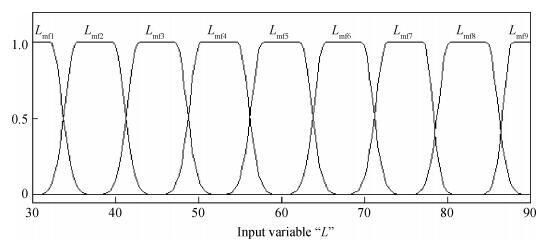
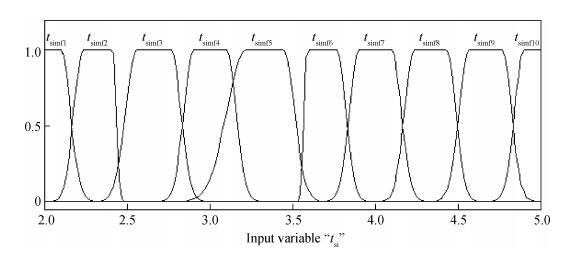
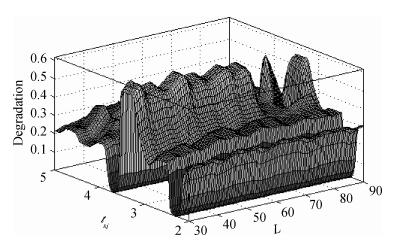
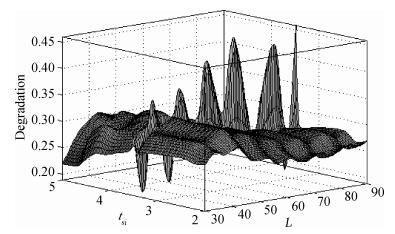
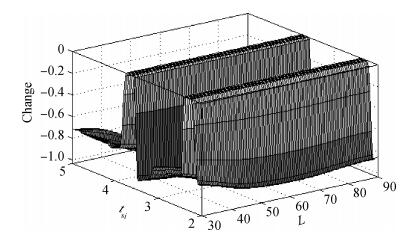
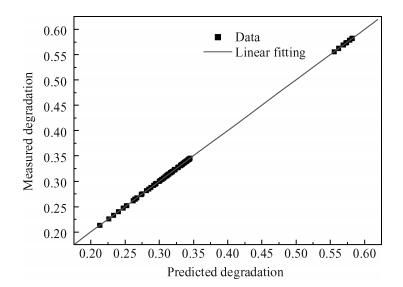
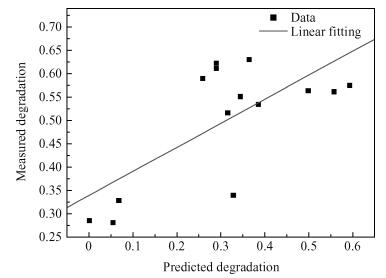
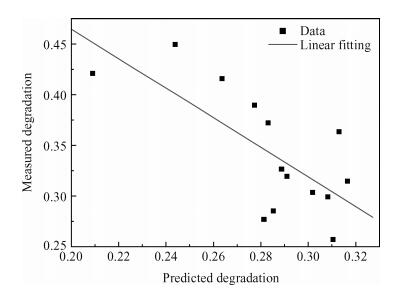
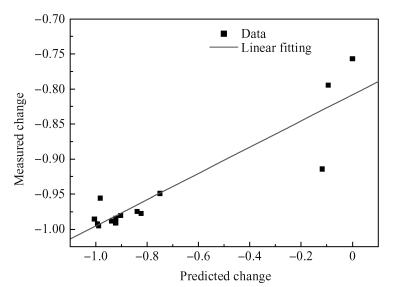
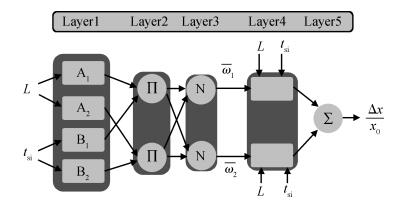
In order to have an accurate description of the DG MOSFET behavior with both an ultra thin silicon body and short channel length, the classical semiconductor equation should be extended to account for the quantum effects becoming dominant at the nanoscale level. The modeling framework based on quantum mechanics tools has received less interest due to the intractability or even the impossibility of getting a self-consistent solution from the Schrödinger/Poisson equations in terms of complexity and computational cost^[8]. Hence, other alternative approaches have been used to study the immunity of DG MOSFETs based on the analysis of subthreshold or small signal parameters before and after stressing. Compact models are widely used for this purpose. These models are built from some simplifying assumptions that are required to reduce the complexity of the resolution approach without significantly altering the quality of the obtained results^[9-12].

In this paper, we investigate the efficiency of an adaptive network-based fuzzy inference system (ANFIS) as a nanoscale thin-film DG MOSFET degradation behavior predictor in the subthreshold regime. This degradation is a complex phenomenon for thin-film MOSFETs, which mainly depends on the hot-carrier effect and quantum confinement. Two geometrical parameters were selected as the input variables to the fuzzy system (channel width and length) in order to predict the change in the subthreshold parameters: threshold voltage, drain-induced barrier lowering and OFF-current ($V_{\rm th}$, DIBL and $I_{\rm OFF})$. In order to get an optimized structure, we tried several types of membership functions during the ANFIS training phase, so that the best one in terms of accuracy could be selected.

The remainder of this paper is organized as follows. In Section 2 we outline the hot-carrier degradation problem, in addition to some of the relevant literature. In Section 3 we present the main concepts relative to the ANFIS architecture and its hybrid learning algorithm. Section 4 depicts in detail the elaboration procedure of the numerical database and the configuration of various device parameters. The computational results are discussed in Section 5, and finally, we give an outlook on the main concluding remarks and future research axes in Section 6.

2. Hot-carrier degradation in MOSFET devices

In response to the actual advances in semiconductor technology, besides the need for faster integrated circuits, the associated MOSFET sizes are continuously downscaled and therefore approaching their physical limits. On the other hand, an extreme difficulty is encountered when scaling some pertinent parameters, which is the case for the supply voltage used to operate these devices. This discrepancy in the velocity of downscaling geometrical and electrical parameters is the origin of a major reliability problem for short channel DG MOSFETs^[13].

During the operation of the device, high electric fields are created in the silicon substrate near the drain-substrate junction due to the formation of a pinch-off region. The intensity of the electric fields increases rapidly with the reduction in the channel length, as predicted by Poisson's equation. When high drain voltages are applied, carriers in the channel and pinch-off regions reach non-equilibrium energy distributions. The energetic carriers qualified as hot carriers trigger various mechanisms at the silicon–oxide interface, and a fraction of the injected hot carriers lose their energy via interaction^[14]. As the amount of injected hot carriers into the oxide depends strongly on the magnitude of the electric field inside the silicon substrate, good estimation of the hot-carrier degradation requires the accurate determination of the electric field distributions in silicon. Many of the approaches proposed for the modeling of hot-carrier distribution are based on the assumption of linear proportionality between the average carrier energy $\langle E \rangle$ and the local electric field $E_{\rm loc}$

$\left\langle E \right\rangle =q\left\langle l \right\rangle E_{\rm loc},$

(1)

where $l$ is the free path of a carrier.

According to the above formula, the maximum energy gained by a carrier is at most equal to that of an elementary charge moving across the potential difference between the drain and source electrodes of the device. If this assertion is true, no carrier injection should take place when the drain–source voltage is below the potential barrier at the Si–SiO$_{2}$ interface. However, significant substrate and gate currents are well detected at drain biases below this value, which constitutes a weak point for this model.

In order to remedy this paradoxical aspect, a more general framework should be used. Under the quantum theory of barrier penetration, carriers going across the local energy barrier at the Si–SiO$_{2}$ interface are considered as particles incident upon a barrier potential. So for each carrier there are two probability measures: a probability of reflection and a probability of transmission^[15]. Both probabilities are related to the opacity of the potential barrier, which depends in turn on many parameters such as the carrier energy. Thus, the carrier injection process is a complex function of the applied biases, the position along the channel, and the type of carrier being injected among other factors, which cannot be modelled analytically in short channel devices.

After the long working duration of a MOSFET device, a fraction of the injected carriers are trapped at defect sites in the oxide or at sites very close to the Si–SiO$_{2}$ interface. Interfacially trapped holes that are positively charged have a high probability of being occupied by the electrons injected into the oxide. An amount of energy is released when the interfacially trapped hole is neutralized by electron capture, and such energy is sufficient to disrupt the chemical bonds near the interface to create an interface trap^[16].

The damage generated by the hot-carrier effect is localized near the drain side since the electric field is maximal at this location. One way to look at this effect is to divide the MOSFET channel into two regions: the fresh region and the damaged region^[17], which results in a threshold voltage that is larger than the fresh part of the channel. Thus, the general trend of a damaged device is that the threshold voltage increases and the drive current decreases as negative trapped-charge builds up or interface trap generation proceeds^[18]. Based on analytical models, such an effect is more pronounced at large drain voltages for larger interface charge region lengths, and the device is severely affected by the presence of negative or positive traps. The threshold voltage near the drain end increases drastically due to the presence of negative interface charge density and reduces gradually for positive interface charge density^[19].

It is common to characterize the device degradation by assessing the shifts before and after the device is stressed. Therefore, the relative variation in a device parameter can be used to estimate the hot-carrier-induced failure time, which indicates that the circuit may no longer function properly where separate equations including empirical constants are developed for gate voltage regions. For example, it is observed that the variation in threshold voltage with stressing time follows a power law^[20] as

$\frac{\Delta V_{\rm th} }{V_{\rm th0} }\approx K_1 t^{n_1},$

(2)

where both fitting parameters $K_{1}$ and $n_{1}$ are dependent on the biasing applied voltages ($V_{\rm ds}$ and $V_{\rm gs})$.

3. The background of ANFIS methodology

In almost artificial intelligence-based models, the cornerstone of the elaborated approaches consists of the development of an interpolative input–output mapping, where an equivalent easy to use scheme is introduced with a set of configurable parameters to be adjusted so that a good match between the predicted and real outputs is obtained. In general, a training algorithm is used to minimize such discrepancy between both outputs. It is worth noting that there is no guarantee that the execution of such algorithms will lead to a global optimum, and therefore a validation phase for these models is a requirement.

The general structure of a fuzzy inference system includes transformations based on membership functions and a fuzzy extended version of the implication rule that maps the input characteristics to a single valued output^[21]. In many cases, the type of membership functions and the rule structure is essentially predetermined by the user's interpretation of the characteristics of the variables in the model. However, in some situations, simply looking at the data cannot specify these aspects and the need for more robust strategies arises.

The ANFIS structure can be considered as a multilayer feed forward network, where neural network learning algorithms and fuzzy reasoning cooperate in the same framework to map nonlinear relationships within complex systems. In this formalism, the input space is divided into many local subregions, which means that several of them can be activated simultaneously by a single input, and then a simple local model given by a linear function is attached to each region^[22]. The ability of ANFIS-based approaches to combine the advantages of the fuzzy computation with the numerical prediction provided by the neural networks has motivated their successful application in various engineering fields such as energy management, machining process and medical diagnosis^[23-25].

In order to highlight the ANFIS architecture and function, we consider a system with two inputs identified in this work as the channel length and thickness, because they are the principal parameters and have a strong influence on the short channel and quantum effects. The number of fuzzy sets attached to each input is denoted by $n$ and $m$, respectively. Hence, the total number of Takagi-Sugeno-Kang fuzzy IF–THEN rules is $n$$m$. The generic expression of such rules is given by

${\rm Rule}\; k:\; {\rm IF} \; L\; {\rm is} \; A_i \; {\rm and} \;t_{\rm si} \;{\rm is}\; B_j \; \\ {\rm THEN}\;f_k =p_k L+q_k t_{\rm si} +r_k, \\ i=\overline {1, m}, \;j=\overline {1, n}, \;k=\overline {1, m n},$

(3)

where $A_{i}$ and $B_{j}$ are the fuzzy sets associated with the geometrical input parameters, and $p_{k}$, $q_{k}$ and $r_{k}$ are the linear parameters in the consequent part of the rule. The corresponding ANFIS architecture is composed of interconnected nodes organized in five functional layers as follows^[26].

(1) Input nodes: each node of this layer deduces the membership grades of the crisp inputs based on the appropriate fuzzy sets using membership functions

$\begin{cases} O_{1, s} =\mu _{A_i}(L), \quad s=\overline {1, m}, \\ O_{1, s} =\mu _{B_j}\left( t_{\rm si} \right), \quad s=\overline {m+1, m+n}. \\ \end{cases}$

(4)

If we assume that we have a generic membership function, then its representation can be given by the following expression

$\mu(x)=F({x;a_{v, =, 1, :, h}}),$

(5)

where $x$ is a generic variable denoting the channel length or thickness, and {$a_{v, =, 1, :, h}$} indicates the parameters' set of the membership function in the premise part of the fuzzy rule that fixes the shape of the membership function.

(2) Rule nodes: nodes in this layer determine the fulfillment degree of the premise part of the rules by input values, using node functions as

$O_{2, k} = t\left( {\mu _{A_i}(L), \mu _{B_j}({t_{\rm si}})} \right)= \mu _{A_i}(L), \\ \mu _{B_j}({t_{\rm si}})=\omega _k, k=\overline {1, m n},$

(6)

where $t$ is a $t$-norm operator such as multiplication or minimum. The $\omega_{k}$ output indicates the firing strength of the $k$th rule.

(3) Average nodes: the role of this third layer is to calculate the ratio of each rule's firing strength to the sum of all the rule's firing strength. So, $\overline {\omega _k }$ is taken as the normalized firing strength

$O_{3, k} =\overline {\omega _k } = \frac{\omega _k }{\sum\limits_{l=1}^{m n} {\omega _l}}, \quad k=\overline {1, m n}.$

(7)

(4) Consequent nodes: each node in this layer computes the normalized output of a rule for current outputs $L$ and $t_{\rm si}$ based on the node function

$O_{4, k} =\overline {\omega _k } f_k =\overline {\omega _k } \left( {p_k L+q_k t_{\rm si} +r_k } \right),$

(8)

where {$p_{k}$, $q_{k}$, $r_{k}$} is the consequent parameter set of rule $k$.

(5) Output nodes: this layer contains only a single node that sums the outputs of the previous layer nodes to obtain the overall network output

$O_{5, 1} =\sum\limits_{k=1}^{m n} {\overline {\omega _k } f_k } =\frac{\sum\limits_{k=1}^{m n} {\omega _k f_k } }{\sum\limits_{k=1}^{m n} {\omega _k } }.$

(9)

The deposition of these layers is illustrated in Fig. 1.

The least square error criterion is used to tune up the ANFIS architecture configuration and is given by

$E=\sum\limits_{o=1}^N {E_o } =\sum\limits_{o=1}^N {\left( {T_o -f_{{\rm out}o} } \right)^2},$

(10)

where $E_{o}$ is the error measure for the $O_{\rm th}$ entry of the given training data set, $T_{o}$ is the desired output of the $O_{\rm th}$ entry and $f_{{\rm out}o}$ is the output of ANFIS using the $O_{\rm th}$ entry. If the premise parameters {$a_{v, =, 1, :, h}$} are fixed, then the output of the whole system can be expressed as a linear combination of the consequent parameters {$p_{k}$, $q_{k}$, $r_{k}$} as

$f=B\theta,$

(11)

where

$f= \begin{bmatrix} f_{\rm out1} \\ \vdots \\ f_{{\rm out}N} \\ \end{bmatrix},$

(12)

$\theta = \begin{bmatrix} p_1\\ q_1\\ r_1 \\ \vdots \\ p_{m n}\\ q_{m n}\\ r_{m n}\\ \end{bmatrix},$

(13)

$B= \begin{bmatrix} \overline {\omega _1} L_1& \overline {\omega _1} t_{\rm si1}& \overline {\omega _1}& \ldots&{\overline {\omega _{m n} } L_1 }& {\overline {\omega _{m n} } t_{\rm si1} }&{\overline {\omega _{m n} } } \\ {\overline {\omega _1 } L_2 }&{\overline {\omega _1 } t_{\rm si2}}&{\overline {\omega _1 } }&\ldots&{\overline {\omega _{m n} } L_2 }& {\overline {\omega _{m n} } t_{\rm si2} }&{\overline {\omega _{m n} } } \\ \vdots&\vdots&\vdots&\ldots &\vdots&\vdots&\vdots \\ {\overline {\omega _1 } L_N }&{\overline {\omega _1 } t_{{\rm si}N} }&{\overline {\omega _1 } } &\ldots &{\overline {\omega _{m n} } L_N }&{\overline {\omega _{m n} } t_{{\rm si}N} }&{\overline {\omega _{m n} } } \\ \end{bmatrix}.$

(14)

Since this equation is a standard linear least square problem, its algebraic solution (the estimator of the unknown matrix $\theta$) can be written as^[27]

$\theta ^\ast =\left( {B^TB} \right)^{-1}B^Tf,$

(15)

where $B^{T}$ and $B^{-1}$ are the transpose and the inverse of matrix $B$, respectively.

The hybrid learning algorithm of the ANFIS combines the gradient method with the least square method to update the parameters, where a generic parameter $\alpha$ formed by the union of the premise and the consequent parameters is updated using the formula

$\Delta \alpha =-\eta \frac{\partial E}{\partial \alpha},$

(16)

with $\eta$ a learning rate.

During the training phase, $\alpha$ is updated at each training epoch in a hybrid manner. More specifically, the consequent parameters of $\alpha$ are updated firstly using a least square algorithm, and the premise parameters are then adjusted by back propagating the errors. However, other alternative methods exist for these optimization processes in learning, such as the genetic algorithm (GA) and particle swarm optimization (PSO) based approaches, but the hybrid learning algorithm remains the most widely used in various applications^{[28, 29]}.

4. Numerical database elaboration

Since the accuracy of a properly trained ANFIS depends on the accuracy and the effective representation of the data used for its training, the database employed for this purpose should be carefully elaborated. The 3-D schematic cross-sectional view of the DG MOSFET device used in this work is depicted in Fig. 2, where an interfacial trap density is assumed to exist near the drain side as a result of the hot-carrier injection. In the elaboration procedure of the training database, different channel lengths and thicknesses are considered for evaluating the range of effects that may be more significant for analysis.

Various subthreshold characteristics ($I_{\rm OFF}$, $V_{\rm th}$ and DIBL) associated to a DG MOSFET structure with different channel lengths and thickness values are obtained numerically using the ATLAS 2-D device simulator^[30]. A total of, 91 sets of data are selected by parsing the channel length range with a step of, 5 nm and the channel thickness range with a step of 0.5 nm. The set of geometrical and electrical parameters conserved during the running of all simulations is given in Table 1.

From the simulated device structure, it can be seen that the channel and the source/drain regions have uniform doping concentrations. All simulations are carried out using two carrier types, the drift–diffusion model without impact ionization, doping concentration-dependant carrier mobility and the electric field-dependant carrier model. SRH recombination/generation is also included in the simulation to account for the leakage currents.

In our work, the subthreshold behavior of the nanoscale DG MOSFET is based on the extraction of some pertinent parameters describing the function of the device. The threshold voltage expresses the gate voltage at which an inversion charge connecting the source/drain electrodes is established. Figure 3 compares the threshold voltage curves for fresh and damaged cases as obtained using numerical simulation. For both cases, the threshold voltage increases with the channel length to reach a constant value, which is the long channel threshold voltage value. As predicted, the damaged device has a higher threshold voltage because a higher applied gate voltage is needed to make the device turn on. Another interesting feature is related to the recorded results for very short channel lengths, where both curves become closer in this case. This can be explained by the strong correlation between the hot-carrier degradation and the short channel effect.

In Fig. 4, the variation in the threshold voltage as function of the channel width is presented with a fixed value of the channel length.

The drain-induced barrier lowering, which reduces the threshold voltage for an increase in drain voltage, is calculated from the difference between the threshold voltages at low and high values of the drain–source voltage, and these are equal to 0.1 and 0.3 V, respectively. As shown in Fig. 5, the DIBL effect is more pronounced for the short channel length devices with and without interface traps.

The OFF-current arises due to the fact that the DG MOSFET is not an ideal switch since there is still some leakage current that flows through it in the OFF-state. For nanoscale devices, both short channel and hot-carrier degradation effects can induce a remarkable change in such drain controllability in the subthreshold regime.

Figure 6 shows the variation in the subthreshold current as a function of the channel length. From this figure, it can be noted that the subthreshold current is pronounced for short channel lengths in both cases (fresh and damaged devices). Another remarkable feature that is clearly shown consists of the diminution of the subthreshold current when interface traps are considered, and this can be due to the trapping of a portion of carriers forming the subthreshold current in addition to the increase in the leakage current for nanoscale devices.

5. Results and discussion

Since the performance of a well-trained ANFIS is strongly affected not only by the exhaustiveness of the training data on the considered interval but also by the type and number of MFs used to characterize the input variables, the training data set is obtained numerically using the 2-D Atlas simulator. The specification of the type and number of MFs is determined by the trial and error approach because no well-established method that can achieve this task optimally exists. So, the MFs are selected heuristically and verified empirically.

In this work, the number of MFs associated with the input variables is determined by exhaustively searching a fixed interval, and we find that the best results are located within the interval [2-15] $\times$ [2-15]. Thus, the number of fuzzy IF-THEN rules for ANFIS is bounded by the following interval [4-225]. The obtained results seem to suggest that using Gaussian combination, generalized bell-shaped and shaped MFs for the threshold voltage, the drain-induced barrier lowering and subthreshold current, respectively, give superior performance compared to other types of MFs. The analytical expressions of the three adopted MFs are indicated below.

The Gaussian combination-shaped MF is defined as

$\mu \left( {x;\sigma _1, \sigma _2, c_1, c_2 } \right)={\rm e}^{-\frac{\left( {x-c_1 } \right)^2}{2\sigma _1^2 }}+{\rm e}^{-\frac{\left( {x-c_2 } \right)^2}{2\sigma _2^2 }}.$

(17)

Whereas the generalized bell-shaped MF is given by

$\mu \left( {x;a, b, c} \right)=\frac{1}{1+\left| {\dfrac{x-c}{a}} \right|^{2b}},$

(18)

and the shaped MF can be formulated as

$\mu \left( {x;a, b, c, d} \right)= \begin{cases} 0, \quad x\leqslant a, \\ 2\left( {\dfrac{x-a}{b-a}} \right)^2, \quad a\leqslant x\leqslant \dfrac{a+b}{2}, \\ 1-2\left( {\dfrac{x-b}{b-a}} \right)^2, \quad \dfrac{a+b}{2}\leqslant x\leqslant b, \\ 1-2\left( {\dfrac{x-c}{d-c}} \right)^2, \quad c\leqslant x\leqslant \dfrac{c+d}{2}, \\ 2\left( {\dfrac{x-d}{d-c}} \right)^2, \quad \dfrac{c+d}{2}\leqslant x\leqslant d, \\ 0, \quad x \geqslant d. \\ \end{cases}$

(19)

The best membership function configuration for the channel length and thickness in the case of the prediction of the threshold voltage relative degradation is illustrated in Figs. 7 and 8.

In order to show the obtained fuzzy rule responses, Figures 9, 10 and 11 depict the ANFIS controller rule surface for the variation in the relative degradation of the threshold voltage, drain-induced barrier lowering and subthreshold current, respectively, as a function of both channel length and thickness. Since the threshold voltage and the drain-induced barrier lowering are correlated, they present a similar behavior characterized by the presence of many local optima, which expresses the modeling complexity of both parameters in contrast to the subthreshold current, which presents a more shaped behavior. A similar situation has been deduced using analytical compact modeling for the case without introducing quantum effects, where the analytical models associated with the threshold voltage are more complicated and require more elaborate methods for their resolution compared to those associated with the subthreshold current^[31-34].

Figures 12 and 13 represent the regression curves of the threshold voltage relative degradation for the training and testing phases. From these figures, it is easy to note that a positive correlation exists between the predicted and numerical values of the relative degradation in the case of the testing data set, which means that a sufficient agreement is satisfied between the predicted and numerical results.

Figures 14 and 15 represent the regression curves of the drain-induced barrier lowering and the subthreshold current relative degradations for the testing phase. In Fig. 14, the correlation between the predicted and numerical values is negative in contrast to Fig. 15, which shows a positive correlation.

From these figures, it can be noticed that for different output variables, the elaborated fuzzy models were able to describe efficiently and with high accuracy, the general tendency behavior of the relative degradation in the threshold voltage, DIBL and subthreshold current. Hence, the adoption of fuzzy logic-based frameworks can be of crucial importance in dealing with nanoscale devices, especially with the inclusion of the parasitic effects occurring at this level and making the analytical modeling an intractable or even an impossible task to achieve.

A summary of the main obtained results for both phases (training and testing phases) is provided in Table 2 for different subthreshold behavior parameters.

As deduced from these results, the correlation coefficient ($R)$ for the testing data is comprised of an absolute value between 0.7 and 0.9. Such a value indicates that we have a strong correlation between the predicted and the measured relative degradation values of the considered parameters' relative degradation. Thus, the performance of our proposed fuzzy approach is acceptable and can be used for further analysis of device behavior in nanoelectronic digital applications.

6. Conclusion

In this paper, an ANFIS-based approach has been proposed to efficiently estimate the relative degradation of the threshold voltage, drain-induced barrier lowering and the subthreshold current, which are considered the principal parameters that characterize CMOS-based devices in the subthreshold regime. Due to the strong influence of the channel length and thickness on the hot-carrier and quantum confinement effects, they were used as the input variables for the fuzzy system. Thanks to the numerical results obtained using the 2D-ATLAS simulator, it was possible to construct the required training database, where a hybrid learning algorithm was used to configure the different premises and consequent parameters included within the IF–THEN rules. The obtained performance demonstrated that the proposed approach can be implemented into circuit simulators in order to study nanoscale CMOS devices, including the hot-carrier degradation effects. The interesting features of the capabilities of ANFIS in dealing with the complexity and uncertainty related to the phenomenological description of device phenomena at a nanoscale level which are statistical in nature, make our proposed approach an adequate tool for future reliability prediction purposes. As a future work direction, the proposed framework can be extended by also including the small signal parameters, which affect the device behavior for analog circuit applications. However, new complex models and simulations should be developed in this case.