| Citation: |
Yawei Guo, Li Li, Peng Ou, Zhida Hui, Xu Cheng, Xiaoyang Zeng. A 0.06 mm2 1.0 V 2.5 mW 10 bit 250 MS/s current-steering D/A converter in 65 nm GP CMOS process[J]. Journal of Semiconductors, 2014, 35(6): 065002. doi: 10.1088/1674-4926/35/6/065002
****
Y W Guo, L Li, P Ou, Z D Hui, X Cheng, X Y Zeng. A 0.06 mm2 1.0 V 2.5 mW 10 bit 250 MS/s current-steering D/A converter in 65 nm GP CMOS process[J]. J. Semicond., 2014, 35(6): 065002. doi: 10.1088/1674-4926/35/6/065002.
|
A 0.06 mm2 1.0 V 2.5 mW 10 bit 250 MS/s current-steering D/A converter in 65 nm GP CMOS process
DOI: 10.1088/1674-4926/35/6/065002
More Information
-
Abstract
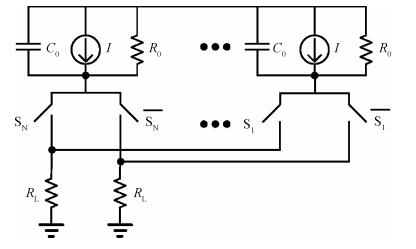
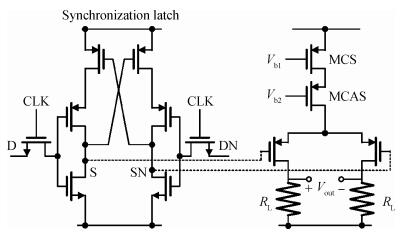
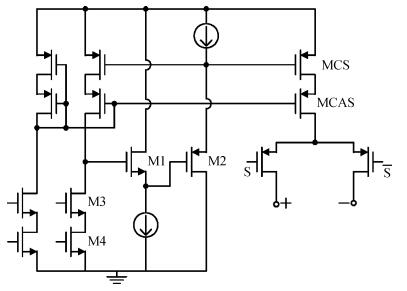
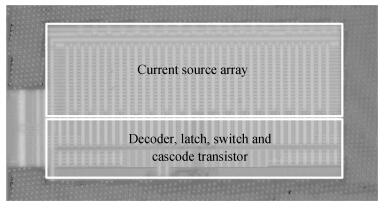
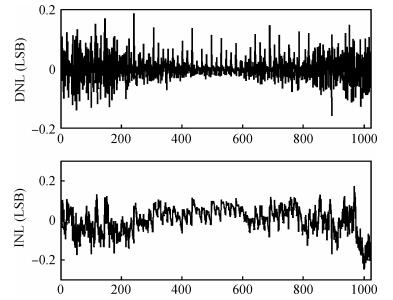
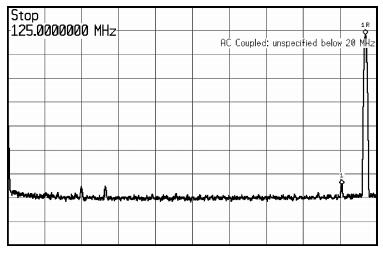
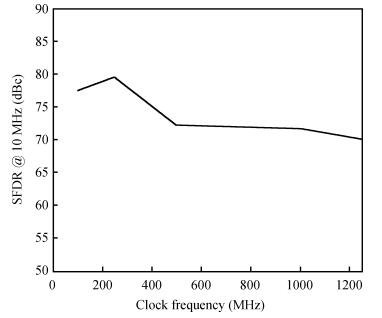
A 10 bit 250 MS/s current-steering digital-to-analog converter is presented. Only standard VT core devices are available for the sake of simplicity and low cost. In order to meet the INL performance, a Monte Carlo model is built to analyze the impact of mismatch on integral nonlinearity (INL) yield with both end-point line and best-fit line. A formula is derived for the relationship of INL and output impedance. The relation of dynamic range and output impedance is also discussed. The double centroid layout is adopted for the current source array in order to mitigate the effect of electrical, process, and temperature gradient. An adapted current mirror is used to overcome the gate leakage of the current source array, which cannot be ignored in the 65 nm GP CMOS process. The digital-to-analog converter occupies 0.06 mm2, and consumes 2.5 mW from a single 1.0 V supply at 250 MS/s. -
References
[1] Lin W, Kuo T. A compact dynamic-performance-improved current-steering DAC with random rotation-based binary-weighted selection. IEEE J Solid-State Circuits, 2012, 37(2):444 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&tp=&arnumber=6059519&contentType=Journals+%26+Magazines&searchField%3DSearch_All%26queryText%3DCurrent+Steering+DAC[2] Van den Bosch A, Borremans M A F, Steyaert M S J, et al. A 10-bit 1-GSample/s Nyquist current-steering CMOS D/A converter. IEEE J Solid-State Circuits, 2001, 36(3):315 doi: 10.1109/4.910469[3] Pelgrom M J M, Duinmaijer A C J, Welbers A P G. Matching properties of MOS transistors. IEEE J Solid-State Circuits, 1989, 24(5):1433 doi: 10.1109/JSSC.1989.572629[4] Razavi B. Principles of data conversion system design. New York:Wiley-IEEE Press, 1994[5] Hui Z, Yuan Y, Guo Y, et al. A low-power digital-to-analog converter for GSM wireless transmitters. Research & Progress of SSE, 2011, 31(1):90 http://en.cnki.com.cn/article_en/cjfdtotal-gtdz201101022.htm[6] Van den Bosch A, Steyaert M, Sansen W. SFDR-bandwidth limitations for high speed high resolution current steering CMOS D/A converters. Proc IEEE Int Conf Electron, Circuits Syst, 1999:1193 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=814383&pageNumber%3D34018%26rowsPerPage%3D100[7] Luschas S, Lee H S. Output impedance requirements for DACs. Proc Int Symp Circuits Syst, 2003, 1:I-861 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1205700[8] Palmers P, Steyaert M S J. A 10-bit 1.6-GS/s 27-mW current-steering D/A converter with 550-MHz 54-dB SFDR bandwidth in 130-nm CMOS. IEEE Trans Circuits Syst Ⅰ:Reguar Papers, 2010, 57(11):2870 doi: 10.1109/TCSI.2010.2052491[9] Bastos J, Marques A M, Steyaert M S J, et al. A 12-bit intrinsic accuracy high-speed CMOS DAC. IEEE J Solid-State Circuits, 1998, 33(12):1959 doi: 10.1109/4.735536[10] Deveugele J, Steyaert M S J. A 10-bit 250-MS/s binary-weighted current-steering DAC. IEEE J Solid-State Circuits, 2006, 41(2):320 doi: 10.1109/JSSC.2005.862342[11] Lee D, Lin Y, Kuo T. Nyquist-rate current-steering digital-to-analog converters with random multiple data-weighted averaging techinque and QN rotated walk switching scheme. IEEE Trans Circuits Syst Ⅱ:Express Briefs, 2006, 53(11):1264 doi: 10.1109/TCSII.2006.882355[12] Gielen G, Dehaene W. Analog and digital circuit design in 65 nm CMOS:end of the road. Proceedings of the Design, Automation and Test in Europe, 2005, 1:37 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1395526[13] Seth S, Sreenath S K. Gate leakage insensitive current mirror circuit. US Patent, No. 7332965B2, 2008 http://www.freepatentsonline.com/7332965.html[14] Chen T, Geens P, van der Plas G, et al. A 14-bit 130-MHz CMOS current-steering DAC with adjustable INL. Proc IEEE Eur Solid-State Circuits Conf (ESSCIRC), 2004:167 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=1356644&sortType%3Dasc_p_Sequence%26filter%3DAND%28p_IS_Number%3A29756%29[15] Zhao Qi, Li Ran, Qiu Dong, et al. a 14-bit 1-GS/s DAC with a programmable interpolation filter in 65 nm CMOS. Journal of Semiconductors, 2013, 34(2):025004 doi: 10.1088/1674-4926/34/2/025004 -
Proportional views






 DownLoad:
DownLoad: