| Citation: |
Zhuomao Zhu, Baoan Bian, Haifeng Shi. Effect of N and Fe codoping on the electronic structure and optical properties of TiO2 from first-principles study[J]. Journal of Semiconductors, 2015, 36(10): 102003. doi: 10.1088/1674-4926/36/10/102003
****
Z M Zhu, B A Bian, H F Shi. Effect of N and Fe codoping on the electronic structure and optical properties of TiO2 from first-principles study[J]. J. Semicond., 2015, 36(10): 102003. doi: 10.1088/1674-4926/36/10/102003.
|
Effect of N and Fe codoping on the electronic structure and optical properties of TiO2 from first-principles study
DOI: 10.1088/1674-4926/36/10/102003
-
Abstract
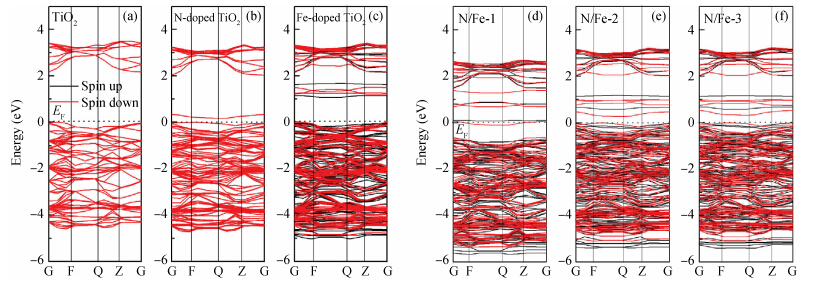
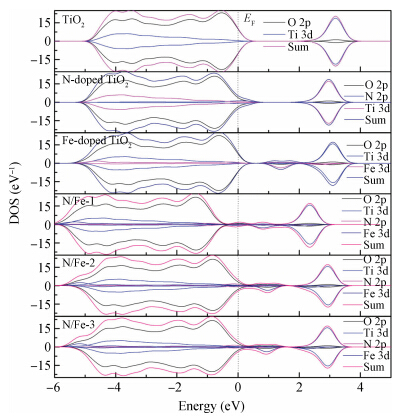
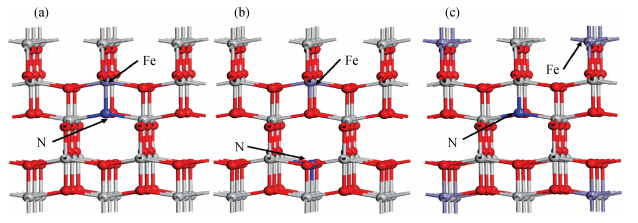
The electronic structure and optical properties of N and Fe codoping TiO2 have been investigated by first-principles calculations based on density functional theory.The calculated results indicate that the stability of N and Fe codoping TiO2 will change at different substitutional sites of N and Fe.The mechanism of band gap narrowing of doping TiO2 is discussed by investigating the density of state.The different substitutional site of N and Fe in codoping TiO2 influences the visible-light absorption.An increased visible-light absorption for doping TiO2 results from the synergistic effect of N and Fe codoping.Therefore, N and Fe codoping may enhance the visible-light photocatalytic activity of TiO2.-
Keywords:
- codoping,
- first-principle,
- electronic structure,
- optical properties
-
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] -
Proportional views





 DownLoad:
DownLoad: