Fig. 1.
(Color online) The 2 $\times $ 2 $\times $ 2 supercell of the cubic perovskite PbTiO$_{3}$. The black, gray, and red spheres represent Pb, Ti, and O atoms, respectively.
DownLoad:
| Citation: |
Peijiang Niu, Jinliang Yan, Delan Meng. The effects of N-doping and oxygen vacancy on the electronic structure and conductivity of PbTiO3[J]. Journal of Semiconductors, 2015, 36(4): 043004. doi: 10.1088/1674-4926/36/4/043004
****
P J Niu, J L Yan, D L Meng. The effects of N-doping and oxygen vacancy on the electronic structure and conductivity of PbTiO3[J]. J. Semicond., 2015, 36(4): 043004. doi: 10.1088/1674-4926/36/4/043004.
|
The effects of N-doping and oxygen vacancy on the electronic structure and conductivity of PbTiO3
DOI: 10.1088/1674-4926/36/4/043004
More Information
-
Abstract
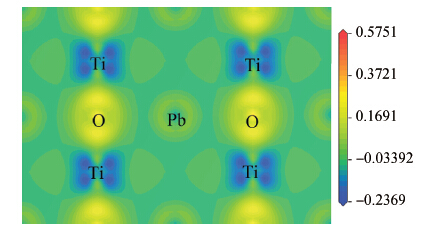
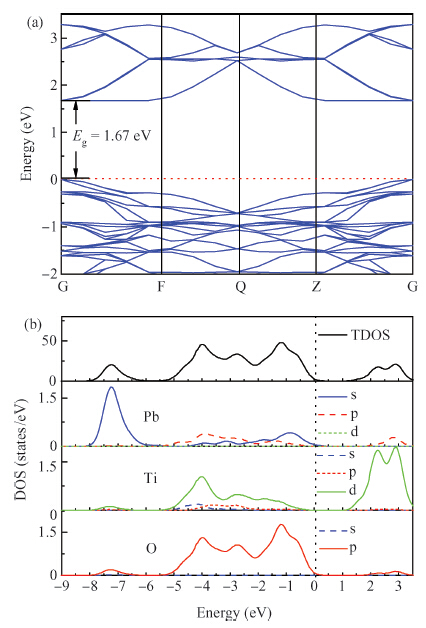
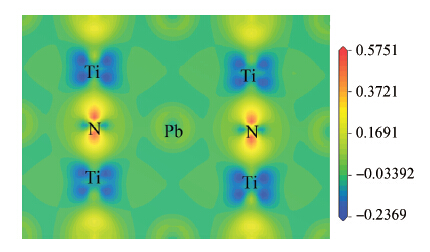
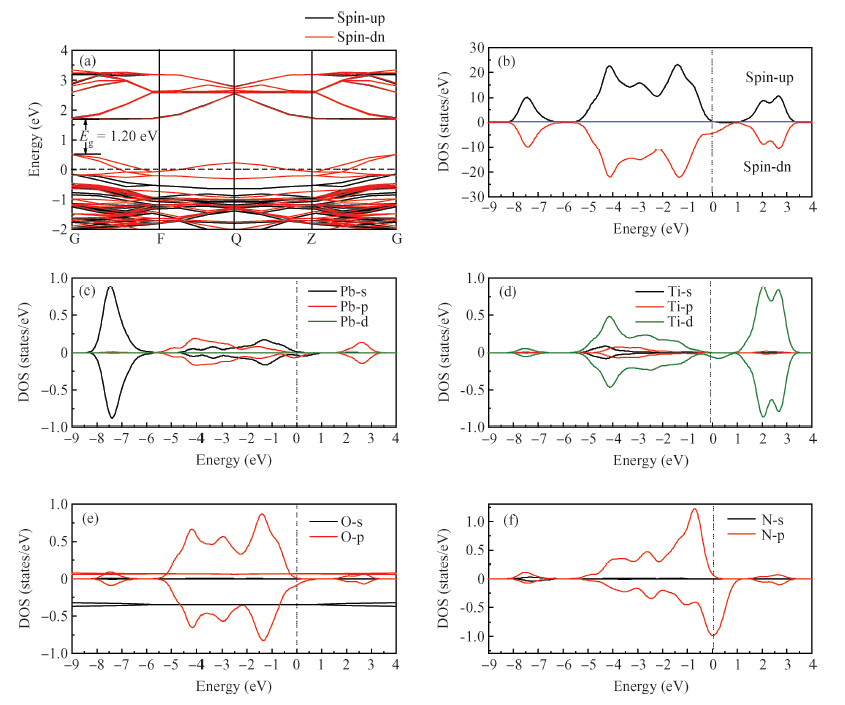
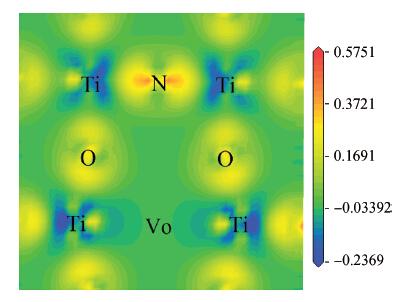
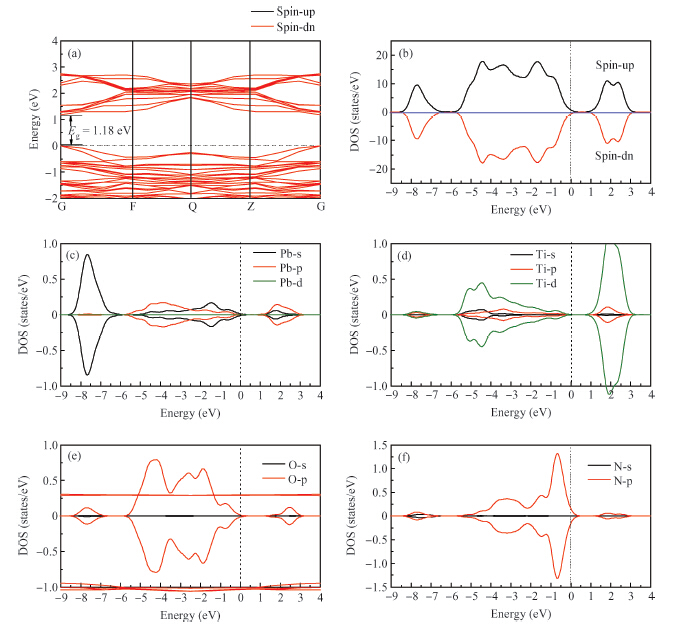
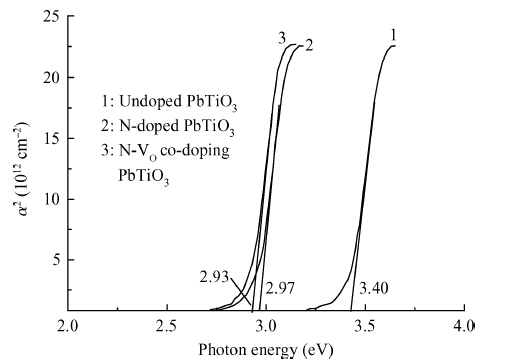
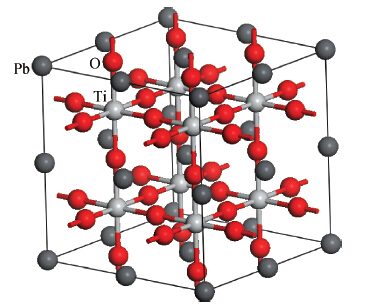
By using spin-polarized density functional theory calculations, the electron density differences, band structures and density of states of p-type N-doped PbTiO3 have been studied. In addition, the oxygen vacancy in N-doped PbTiO3 is also discussed. After the nitrogen dopant is introduced into the crystal, the N-doped PbTiO3 system is spin-polarized, the spin-down valance bands move to a high energy level and the Fermi energy level moves to the top of the valance bands, finally the band gap is narrowed. In this process, the N-doped PbTiO3 shows typical p-type semiconductor characteristics. When an oxygen vacancy and N impurity coexist in PbTiO3, there is no spin-polarized phenomenon. The conduction bands move downward and the acceptors are found to be fully compensated. The calculation results are mostly consistent with the experimental data. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] -
Proportional views
