| Citation: |
Tanu Goyal, Manoj Kumar Majumder, Brajesh Kumar Kaushik. Propagation delay and power dissipation for different aspect ratio of single-walled carbon nanotube bundled TSV[J]. Journal of Semiconductors, 2015, 36(6): 065001. doi: 10.1088/1674-4926/36/6/065001
****
T Goyal, M K Majumder, B K Kaushik. Propagation delay and power dissipation for different aspect ratio of single-walled carbon nanotube bundled TSV[J]. J. Semicond., 2015, 36(6): 065001. doi: 10.1088/1674-4926/36/6/065001.
|
Propagation delay and power dissipation for different aspect ratio of single-walled carbon nanotube bundled TSV
DOI: 10.1088/1674-4926/36/6/065001
More Information
-
Abstract
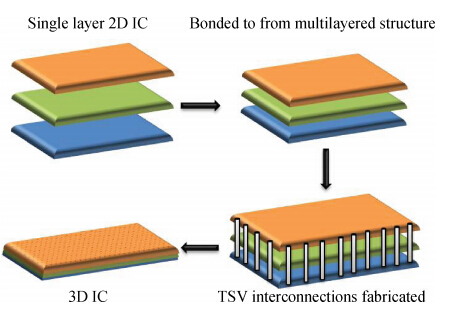
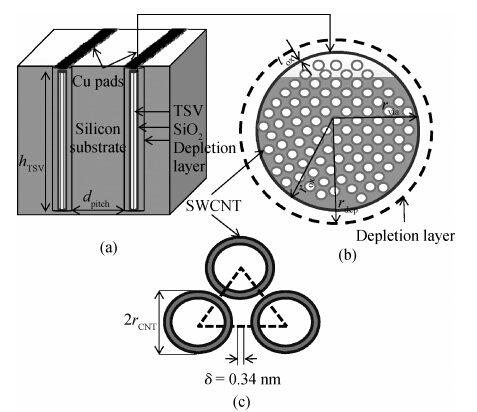
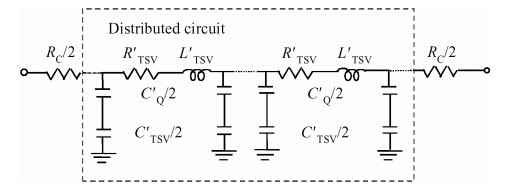
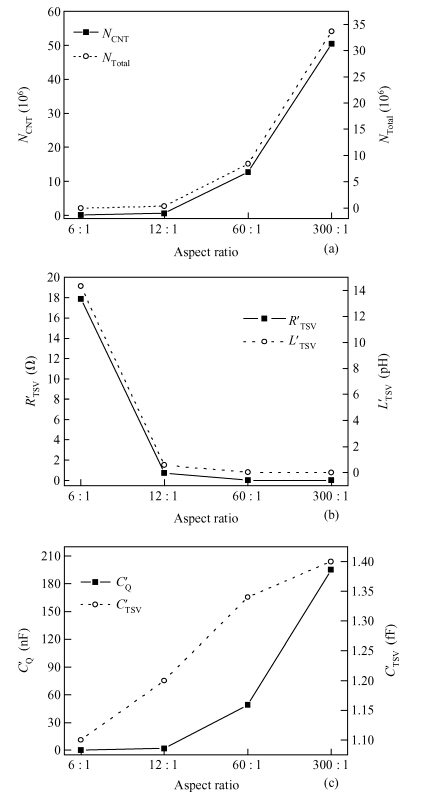
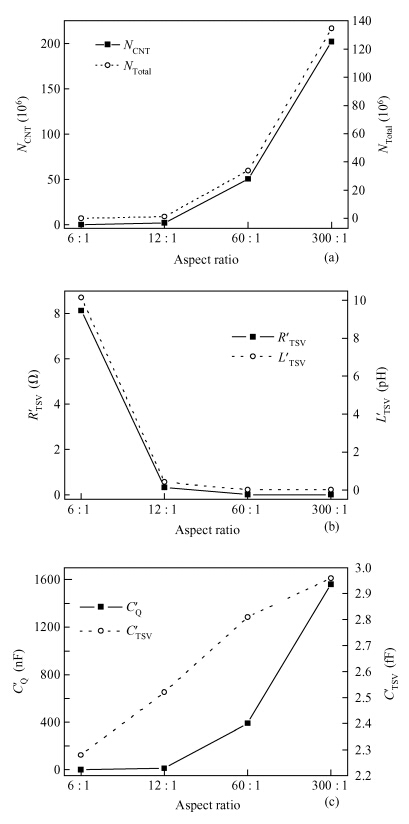
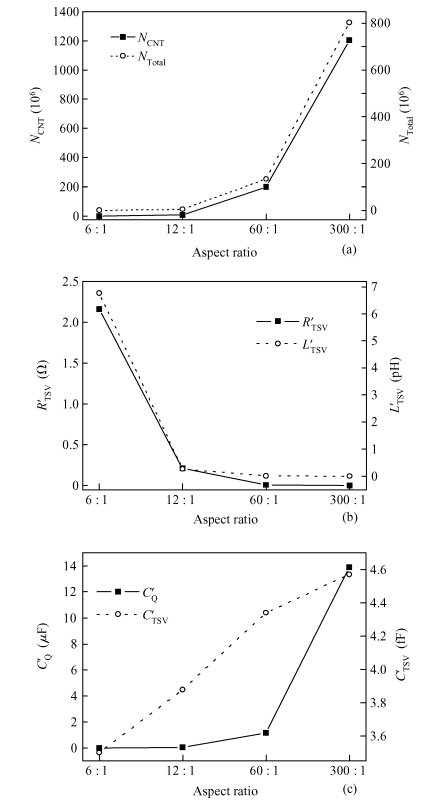
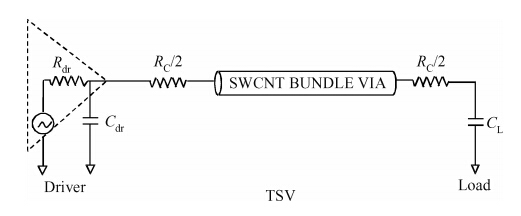
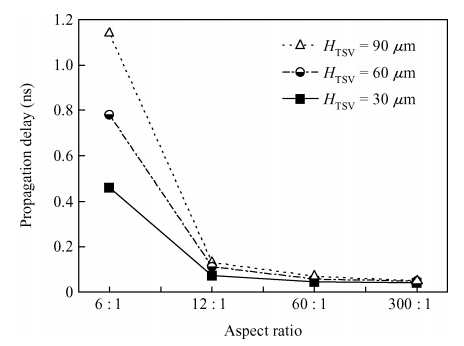
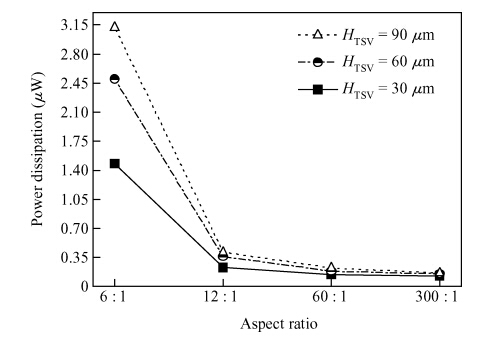
Through-silicon vias (TSVs) have provided an attractive solution for three-dimensional (3D) integrated devices and circuit technologies with reduced parasitic losses and power dissipation, higher input-output (I/O) density and improved system performance. This paper investigates the propagation delay and average power dissipation of single-walled carbon nanotube bundled TSVs having different via radius and height. Depending on the physical configuration, a comprehensive and accurate analytical model of CNT bundled TSV is employed to represent the via (vertical interconnect access) line of a driver-TSV-load (DTL) system. The via radius and height are used to estimate the bundle aspect ratio (AR) and the cross-sectional area. For a fixed via height, the delay and the power dissipation are reduced up to 96.2% using a SWCNT bundled TSV with AR = 300 : 1 in comparison to AR = 6 : 1. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] -
Proportional views





 DownLoad:
DownLoad: