1. Introduction

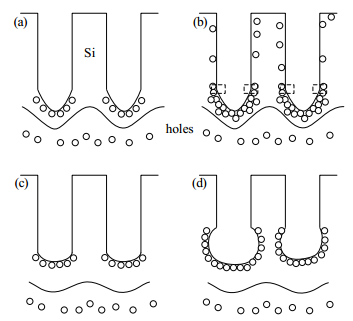
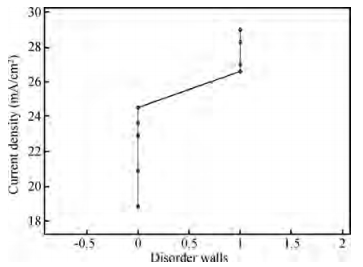
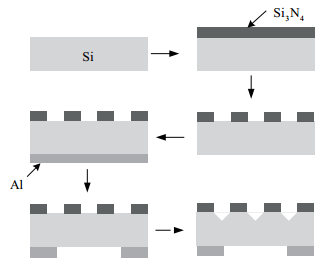
The fabrication of ordered, high aspect-ratio (HAR) microstructures in porous silicon by photo-assisted electrochemical etching (PAEE) is an important technology because of its widespread applications^[1-5], such as energy devices, X-ray imaging devices, microchannel plates, and photonic crystals. Over the last twenty years, different morphologies including pores, pillars, wall arrays, and other ordered patterns in porous silicon substrates have been obtained through the use of PAEE in hydrofluoric acid electrolyte^[6-8]. In this work, HAR wall arrays act as the phase gratings used in X-ray differential phase-contrast imaging (DPCI).

Generally, in PAEE it is possible for holes generated in the sidewalls to move to the interface, resulting in the dissolution of the sidewalls^[9]. This results in nonuniform wall widths. To obtain uniform walls, Lehmann's formula was modified to increase the current density as the etching time increases. Unfortunately, this results in disordered etching at the bottom of the wall arrays. As previously reported in References ^[10-14], there are many factors that influence the formation of microstructures by PAEE, including voltage, current density, silicon resistivity, illumination, and electrolyte concentration, and their induced etching results were listed.

In this paper, focusing on the causes of disordered walls, the effect of etching parameters, particularly the applied voltage and the current density, on the etching process for 5-inch n-type silicon wafers are investigated. The contrast experiments show that the morphology of the wall arrays can be controlled by regulating both the applied voltage and the current density. Finally, a wall array of 5.6 μm period and 55 μm depth was achieved at a voltage of 3 V and a monotonically increasing current density ranging from 22.9 to 24.5 mA/cm².

2. Experiments

The silicon wafers used in this study were 5 inches in diameter, n-type, (100) oriented, 5-7 Ω·cm resistivity, and 425 μm thick. An aluminum layer with thickness of 1 μm was deposited on the back side of the wafer to form an ohmic contact, and a 0.3 μm silicon nitride layer was deposited on the front side. We defined periodic patterns of wall arrays by standard photolithography and RIE. The period of the wall arrays was 5.6 μm and the wall width was 2.8 μm. Next, inverted pyramid-shaped grooves were created by KOH anisotropic etching at a temperature of 80 ℃ and used as the HF-etching seeds. The prestructuring process is shown in Figure 1.

The PAEE setup consisted of five main parts: the Teflon container, the power supply, the illumination system, the solution circulation system, and the cooling system, as previously described^[14]. The electrolyte solution consisted of deionized water, HF (5% by weight) and ethanol. Ethanol was added to remove hydrogen bubbles and to smooth the surface of walls. All experiments were carried out based on Lehmann's formula^[10].

$${{J}_{\text{ps}}}=C{{c}^{1.5}}\text{exp}\left( -{{E}_{\text{a}}}/{{K}_{\text{B}}}T \right),$$

(1)

where $J_{\rm ps}$ is the critical current density, C=3300 A/cm², ${{E}_{\text{a}}}$=0.345 eV, $K_{\rm B}$ is the Boltzmann constant, c is the HF concentration, and T is the solution temperature (294 K in our cases).

A voltage of 3 V and a current density of 22.9 mA/cm² were applied to the silicon wafer. The result is shown in Figure 2(a). Note that the width of walls gradually increases from the top (2.2 μm) to the bottom (3.2 μm). According to the previous Reference^[9], wall arrays with uniform widths can be obtained by increasing the current density as the etching depth increases. Holding voltage constant at 3 V, the current density was increased from 22.9 to 27.8 mA/cm². As a result, a more uniform wall array was achieved. However, as shown in Figure 2(b), disordered walls were simultaneously observed in the middle of the wall array (annotated with black lines). Furthermore, the width of the trenches and the depth of the wall arrays became irregular.

3. Results and discussion

For electrochemical etching of n-type silicon, the sample is typically illuminated using LEDs or tungsten halogen lamps at the back surface[10, 11]. The illumination generates electron hole pairs in the path to the penetration depth. Then, holes move towards the front side of the silicon. To control the distribution of holes in the interface between the silicon and the electrolyte, a voltage must be applied and pyramid-shaped grooves must be established. The voltage can establish an electrical field along the silicon surface and collect holes at the tips of these grooves. This depletes the space charge region (SCR), which causes a passivation of the walls. In the PAEE process, a balance is maintained between the charge transfer and the mass transport. The current density is an important parameter representing the relationship between charge transfer and mass transport^[10].

Ideally, all holes generated beneath the pyramid-shaped grooves would be attracted to the tips and react with HF, with none generated in the SCR. However, light with a wavelength less than 1100 nm can pass through silicon to a long penetration depth and excite electron hole pairs. Therefore, holes inevitably generate in the SCR and move to the interface of the sidewalls. These holes are then consumed in the sidewalls, causing them to dissolve. As the depth increases, the walls gradually thin at the top due to the long dissolution time (in comparison to the bottom). Therefore, a measure of gradually increasing current density was employed to improve wall width uniformity. However, as shown in Figure 2(b), disordered walls appeared when the current density increased to approximately 25.4 mA/cm², corresponding to an etching depth of 29 μm.

The theory of SCR can be used to explain some of the etching results^[15-17]. According to Schottky contact theory, the width of the SCR w, is given by^[11]:

$$w=\sqrt {\frac{2\varepsilon_{0} \varepsilon_{\rm si} V_{\rm eff} }{qN_{\rm D} }},$$

(2)

where $\varepsilon_{\rm si}$ is the dielectric permittivity of the silicon, $V_{\rm eff}$ is the effective voltage, and $N_{\rm D}$ is the doping density. For a given silicon wafer, w is proportional to the square root of $V_{\rm eff}$. The larger the effective voltage, the wider the SCR becomes^[17].

Theoretically, the effect of the applied voltage can be divided into two aspects in PAEE: the protection of the sidewalls from dissolution, reliant on matching the SCR formed by the voltage and the walls width; and the effect constraining the holes in the tips of the pyramid shaped grooves, dependent on the distance from the tips to the electric field line. Sidewalls dissolution would be inevitable if the SCR were less than half of the walls width^[16]. When the applied voltage is increased to the critical value, etching occurs regularly under the critical current density with the holes distributed both in the tips and along the surface of tips, as shown in Figure 3(a). As current density is increased through illumination, more holes are generated and accumulate in and on the tips, as shown in Figure 3(b). A portion of these holes contributes to normal trench etching, but others collect at some sites, as shown in the dotted line regions in Figure 3(b). These regions attract more holes, resulting in preferential etching. Hence, trenches including these sites become wider, making the walls thinner and more disordered. At higher hole concentration, over-etching and electropolishing can occur. As the applied voltage is increased, the electric field line is pushed further away from the tips and the SCR increases in width, as shown in Figure 3(c). The morphology of the tips changes to flat, which results in the accumulation of more holes in those sites shown in Figure 3(b). At this condition, a small current density may be appropriate to ensure normal etching. Furthermore, increased morphology sensitivity to changes in current density can be obtained. As the current density is increased, more holes concentrate in and on the tips, further worsening wall disorder, as shown in Figure 3(d). Conversely, it will be difficult for the appearing of disordered walls with decreasing the voltage to less than critical value. Conclusively, maintaining the width of walls and increasing current density are contrary processes, because a large current density corresponds to a large duty ratio. The holes become heterogeneously distributed when both parameters are increased to large values, which leads to morphology changes.

To validate this deduction, a set of experiments was implemented, with voltages at 2.7, 3.0, 3.5, and 3.5 V, and current densities at 29.1, 18.9, 22.9, and 25.1 mA/cm², as shown in Table 1.

Sample #1 was etched with a voltage of 2.7 V and a current density of 29.1 mA/cm², larger than the critical value of 22.9 mA/cm². There are no disordered walls, but some pore walls remained. This indicates that the lower voltage can bear the larger current density. Sample #2 was etched with a voltage of 3.0 V and a current density of 18.9 mA/cm², less than the critical value. Again, there were no disordered walls, but some pore walls still remained near the bottom. Sample #3 and sample #4 were both etched with voltages of 3.5 V. They were subjected to current densities of 22.9 mA/cm² and 25.1 mA/cm², respectively. Disordered walls occurred in the middle and the bottom, but the trenches were clear of pore walls. The disordered walls became more prevalent as the current density was increased. Side views of the samples obtained by scanning electron microscope (SEM) are shown in Figure 4. The positions of the disordered walls are not regular.

At the critical voltage of 3 V, three regions can be distinguished: incomplete, complete, and disordered etching. Under these conditions, the current density becomes the influencing factor on the wall array etching. Some experiments were implemented to distinguish the condition of disordered walls at a voltage of 3 V and current densities varying from 18.9 to 29 mA/cm², as shown in Figure 5. The circles represent the applied current density. A binary representation was used to indicate the conditions of “no disordered walls” (0) and “disordered walls” (1). Between 24.5 and 26.5 mA/cm², the number of disordered walls was significantly less than experiments where the current density was larger than 26.5 mA/cm². To fabricate wall arrays with uniform widths and no disordered features, the modified Lehmann formula must be limited to a maximum current density. Finally, an experiment was implemented at the critical voltage, with current density increased monotonically from 22.9 to 24.5 mA/cm². A wall array with a period of 5.6 μm and a depth of 55 μm was achieved and is shown in Figure 6.

4. Conclusions

Compensating current density can provide uniform wall widths in PAEE for 5-inch HAR wall arrays, but can also result in disordered walls. In this paper, an analysis of this effect from the point of view of the applied voltage and the current density was presented. Then, various values of voltage and current density were applied to validate the analysis. Furthermore, a series of experiments were implemented at a voltage of 3 V, with current density varying from 18.9 to 29 mA/cm², to determine conditions for avoiding disordered walls. Finally, a uniform wall array with a period of 5.6 μm and a depth of 55 μm was achieved by monotonically increasing the current density from 22.9 to 24.5 mA/cm².