| Citation: |
Huajun Chen, Changzhao Chen, Yang Li, Xianwen Fang. Monolayer-molybdenum-disulfide-based nano-optomechanical transistor andewline tunable nonlinear responses[J]. Journal of Semiconductors, 2016, 37(11): 114004. doi: 10.1088/1674-4926/37/11/114004
****
H J Chen, C Z Chen, Y Li, X W Fang. Monolayer-molybdenum-disulfide-based nano-optomechanical transistor andewline tunable nonlinear responses[J]. J. Semicond., 2016, 37(11): 114004. doi: 10.1088/1674-4926/37/11/114004.
|
Monolayer-molybdenum-disulfide-based nano-optomechanical transistor andewline tunable nonlinear responses
DOI: 10.1088/1674-4926/37/11/114004
More Information
-
Abstract
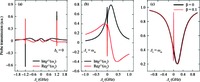
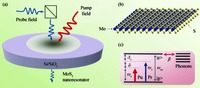
Atomically thin two-dimensional semiconductor nanomaterials have attained considerable attention currently. Here, we present a nano-optomechanical system based on a suspended monolayer molybdenum disulfide (MoS2). The linear and nonlinear coherent optical properties of this system, and the phenomenon of phonon-induced transparency are demonstrated. The transmission of the probe field can be manipulated by the power of a second ‘gating' (pump) field, which indicates a promising candidate for an optical transistor. We further study the nonlinear effect of the system, and the optical Kerr effect of the monolayer MoS2 resonator can be regulated under different parameter regimes. This scheme proposed here may indicate potential chip-scale applications of monolayer MoS2 resonator in quantum information with the currently popular pump-probe technology. -
References
[1] Neto A H C, Guinea F, Peres N M R, et al. The electronic properties of graphene. Rev Mod Phys, 2009, 81(1):109 doi: 10.1103/RevModPhys.81.109[2] Chen C, Rosenblatt S, Bolotin K I, et al. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nature Nanotechnology, 2009, 4(12):861 doi: 10.1038/nnano.2009.267[3] Ganatra R, Zhang Q. Few-layer MoS2:a promising layered semiconductor. ACS Nano, 2014, 8(5):4074 doi: 10.1021/nn405938z[4] Mak K F, Lee C, Hone J, et al. Atomically thin MoS2:a new direct-gap semiconductor. Phys Rev Lett, 2010, 105(13):136805 doi: 10.1103/PhysRevLett.105.136805[5] He K, Poole C, Mak K F, et al. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett, 2013, 13(6):2931 doi: 10.1021/nl4013166[6] Eda G, Yamaguchi H, Voiry D, et al. Photoluminescence from chemically exfoliated MoS2. Nano Lett, 2011, 11(12):5111 doi: 10.1021/nl201874w[7] Lee H S, Min S W, Chang Y G, et al. MoS2 nanosheet phototransistors with thickness modulated optical energy gap. Nano Lett, 2012, 12(7):3695 doi: 10.1021/nl301485q[8] Lopez-Sanchez O, Lembke D, Kayci M, et al. Ultrasensitive photodetectors based on monolayer MoS2. Nat Nanotechnol, 2013, 8(7):497 doi: 10.1038/nnano.2013.100[9] Fontana M, Deppe T, Boyd A K, et al. Electron-hole transport and photovoltaic effect in gated MoS2 Schottky junctions. Sci Rep, 2013, 3, 1634 http://cn.bing.com/academic/profile?id=1974974080&encoded=0&v=paper_preview&mkt=zh-cn[10] Radisavljevic B, Radenovic A, Brivio J, et al. Single-layer MoS2 transistors. Nat Nanotechnol, 2011, 6(3):147 doi: 10.1038/nnano.2010.279[11] Krasnozhon D, Lembke D, Nyffeler C, et al. MoS2 transistors operating at gigahertz frequencies. Nano Lett, 2014, 14(10):5905 doi: 10.1021/nl5028638[12] Li H, Yin Z, He Q, et al. Fabrication of single-and multilayer MoS2 film-based field-effect transistors for sensing NO at room temperature. Small, 2012, 8(1):63 doi: 10.1002/smll.201101016[13] Perkins F K, Friedman A L, Cobas E, et al. Chemical vapor sensing with monolayer MoS2. Nano Lett, 2013, 13(2):668 doi: 10.1021/nl3043079[14] Liu B, Chen L, Liu G, et al. High-performance chemical sensing using Schottky-contacted chemical vapor deposition grown monolayer MoS2 transistors. ACS Nano, 2014, 8(5):5304 doi: 10.1021/nn5015215[15] Weber P, Guttinger J, Tsioutsios I, et al. Coupling graphene mechanical resonators to superconducting microwave cavities. Nano Lett, 2014, 14(5):2854 doi: 10.1021/nl500879k[16] Singh V, Bosman S J, Schneider B H, et al. Optomechanical coupling between a multilayer graphene mechanical resonator and a superconducting microwave cavity. Nat Nanotechnol, 2014, 9(10):820 doi: 10.1038/nnano.2014.168[17] Lee J, Wang Z, He K, et al. High frequency MoS2 nanomechanical resonators. ACS Nano, 2013, 7(7):6086 doi: 10.1021/nn4018872[18] van Leeuwen R, Castellanos-Gomez A, Steele G A, et al. Time-domain response of atomically thin MoS2 nanomechanical resonators. Appl Phys Lett, 2014, 105(4):041911 doi: 10.1063/1.4892072[19] Castellanos-Gomez A, van Leeuwen R, Buscema M, et al. Single-layer MoS2 mechanical resonators. Adv Mater, 2013, 25(46):6719 doi: 10.1002/adma.v25.46[20] Bertolazzi S, Brivio J, Kis A. Stretching and breaking of ultrathin MoS2. ACS Nano, 2011, 5(12):9703 doi: 10.1021/nn203879f[21] Castellanos-Gomez A, Poot M, Steele G A, et al. Elastic properties of freely suspended MoS2 nanosheets. Adv Mater, 2012, 24(6):772 doi: 10.1002/adma.201103965[22] Lee C, Yan H, Brus L E, et al. Anomalous lattice vibrations of single-and few-layer MoS2. ACS Nano, 2010, 4(5):2695 doi: 10.1021/nn1003937[23] Kioseoglou G, Hanbicki A T, Currie M, et al. Valley polarization and intervalley scattering in monolayer MoS2. Appl Phys Lett, 2012, 101(22):221907 doi: 10.1063/1.4768299[24] Molina-Sanchez A, Wirtz L. Phonons in single-layer and few-layer MoS2 and WS2. Phys Rev B, 2011, 84(15):155413 doi: 10.1103/PhysRevB.84.155413[25] Li T. Ideal strength and phonon instability in single-layer MoS2. Phys Rev B, 2012, 85(23):235407 doi: 10.1103/PhysRevB.85.235407[26] Wang Z, Lee J, He K, et al. Embracing structural nonidealities and asymmetries in two dimensional nanomechanical resonators. Sci Rep, 2014, 4:3919 http://cn.bing.com/academic/profile?id=2128957616&encoded=0&v=paper_preview&mkt=zh-cn[27] Suzuki H, Yamaguchi N, Izumi H. Theoretical and experimental studies on the resonance frequencies of a stretched circular plate:application to Japanese drum diaphragms. Acoust Sci Technol, 2009, 30(5):348 doi: 10.1250/ast.30.348[28] Chen H J, Zhu K D. Coherent optical responses and their application in biomolecule mass sensing based on a monolayer MoS2 nanoresonator. J Opt Soc Am B, 2014, 31(7):1684 doi: 10.1364/JOSAB.31.001684[29] Li J J, Zhu K D. All-optical mass sensing with coupled mechanical resonator systems. Phys Rep, 2013, 525(3):223 doi: 10.1016/j.physrep.2012.11.003[30] Xu X, Sun B, Berman P R, et al. Coherent optical spectroscopy of a strongly driven quantum dot. Science, 2007, 317(5840):929 doi: 10.1126/science.1142979[31] Chen H J, Zhu K D. Graphene-based nanoresonator with applications in optical transistor and mass sensing. Sensors, 2014, 14(9):16740 doi: 10.3390/s140916740[32] Safavi-Naeini A H, Alegre T P M, Chan J, et al. Electromagnetically induced transparency and slow light with optomechanics. Nature, 2011, 472(7341):69 doi: 10.1038/nature09933[33] Okamoto H, Gourgout A, Chang C Y, et al. Coherent phonon manipulation in coupled mechanical resonators. Nat Phys, 2013, 9(8):480 doi: 10.1038/nphys2665[34] Yan H, Low T, Guinea F, et al. Tunable phonon-induced transparency in bilayer grapheme nanoribbons. Nano Lett, 2014, 14(8):4581 doi: 10.1021/nl501628x -
Proportional views





 DownLoad:
DownLoad: