J. Semicond. > 2016, Volume 37 > Issue 2 > 022002
|

SEMICONDUCTOR PHYSICS

Impact of stray charge on interconnect wire via probability model of double-dot system

Xiangye Chen1, , Li Cai2, Qiang Zeng1 and Xinqiao Wang1

+ Author Affiliations

 Corresponding author: Xiangye Chen, Email: conquor_fighter@qq.com

DOI: 10.1088/1674-4926/37/2/022002

PDF

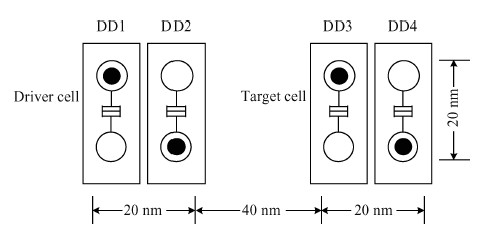
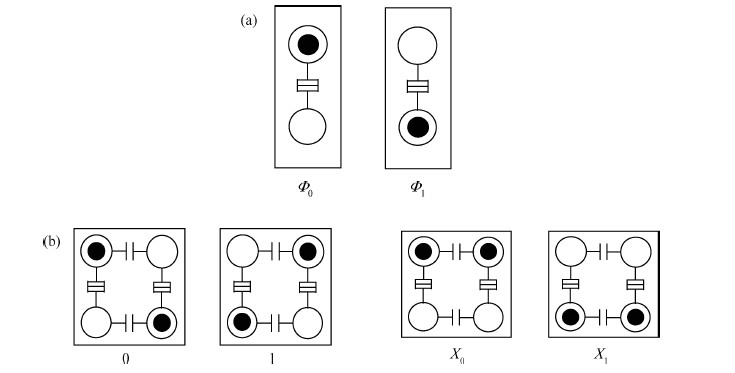
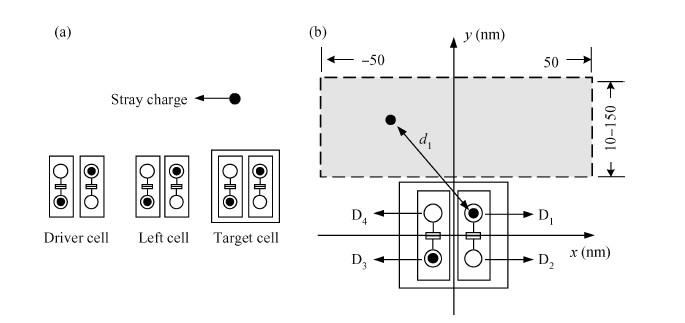
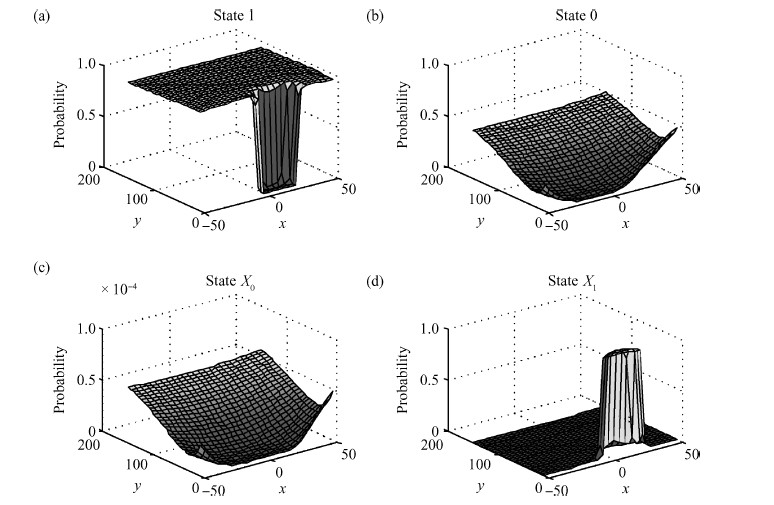
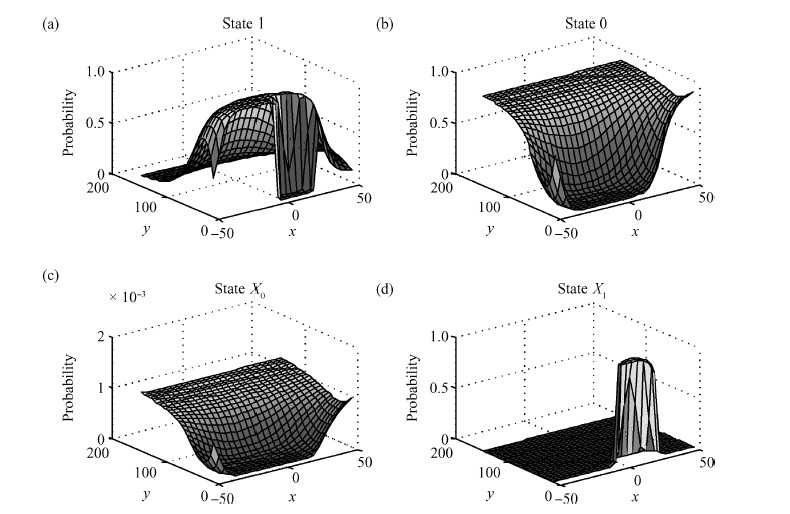
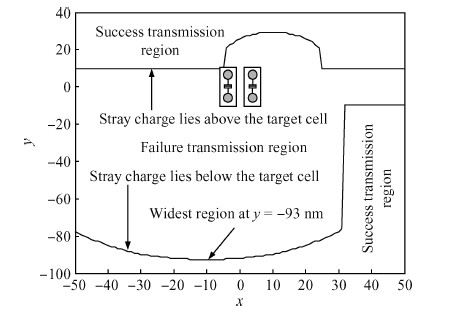
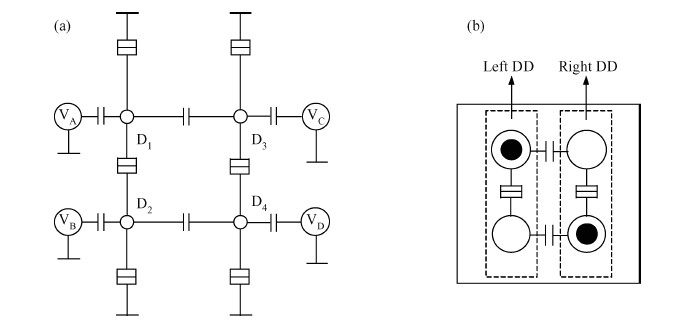
Abstract: The behavior of quantum cellular automata (QCA) under the influence of a stray charge is quantified. A new time-independent switching paradigm, a probability model of the double-dot system, is developed. Superiority in releasing the calculation operation is presented by the probability model compared to previous stray charge analysis utilizing ICHA or full-basis calculation. Simulation results illustrate that there is a 186-nm-wide region surrounding a QCA wire where a stray charge will cause the target cell to switch unsuccessfully. The failure is exhibited by two new states' dominating the target cell. Therefore, a bistable saturation model is no longer applicable for stray charge analysis.

Key words: quantum cellular automata, interconnect wire, stray charge, probability model of double-dot system



[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
Fig. 1.  (a) Schematic diagram of an integrated cell[11]. (b) A two double-dot system consisting of an integrated cell[23].

DownLoad: Full-Size Img PowerPoint
Fig. 2.  Schematic diagram of a target DD and its driver cells.

DownLoad: Full-Size Img PowerPoint
Fig. 3.  States in probability model. (a) Two states exhibited by a DD cell. (b) Four states exhibited by an integrated cell.

DownLoad: Full-Size Img PowerPoint
Fig. 4.  Schematic diagram of a two cells wire.

DownLoad: Full-Size Img PowerPoint
Fig. 5.  Target cell performance with the driver cell of ‘1’.

DownLoad: Full-Size Img PowerPoint
Fig. 6.  Target cell performance with the driver cell of ‘0’.

DownLoad: Full-Size Img PowerPoint
Fig. 7.  Target cell performance with the driver cell of ‘0’.

DownLoad: Full-Size Img PowerPoint
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]

    • Search

    Advanced Search >>

    GET CITATION

    shu

    Export: BibTex EndNote

    Article Metrics

    Article views: 2602 Times PDF downloads: 11 Times Cited by: 0 Times

    History

    Received: 20 May 2015 Revised: Online: Published: 01 February 2016

    Catalog

      Email This Article

      User name:
      Email:*请输入正确邮箱
      Code:*验证码错误
      Send
      Article Navigation >  Journal of Semiconductors  > 2016  >  37(2): 022002
      Xiangye Chen, Li Cai, Qiang Zeng, Xinqiao Wang. Impact of stray charge on interconnect wire via probability model of double-dot system[J]. Journal of Semiconductors, 2016, 37(2): 022002. doi: 10.1088/1674-4926/37/2/022002 ****X Y Chen, L Cai, Q Zeng, X Q Wang. Impact of stray charge on interconnect wire via probability model of double-dot system[J]. J. Semicond., 2016, 37(2): 022002. doi: 10.1088/1674-4926/37/2/022002.
      Citation:
      Xiangye Chen, Li Cai, Qiang Zeng, Xinqiao Wang. Impact of stray charge on interconnect wire via probability model of double-dot system[J]. Journal of Semiconductors, 2016, 37(2): 022002. doi: 10.1088/1674-4926/37/2/022002 ****
      X Y Chen, L Cai, Q Zeng, X Q Wang. Impact of stray charge on interconnect wire via probability model of double-dot system[J]. J. Semicond., 2016, 37(2): 022002. doi: 10.1088/1674-4926/37/2/022002.
      shu

      Impact of stray charge on interconnect wire via probability model of double-dot system

      DOI: 10.1088/1674-4926/37/2/022002
      • 1.

        Flight Instructor Training Base, Air Force Aviation University, Bengbu 233000, China

      • 2.

        College of Science, Air Force Engineering University, Xi'an 710051, China

      Funds:

      Project supported by the National Natural Science Foundation of China (No. 61172043) and the Key Program of Shaanxi Provincial Natural Science for Basic Research (No. 2011JZ015).

      More Information
      • Corresponding author: Email: conquor_fighter@qq.com
      • Received Date: 2015-05-20
      • Accepted Date: 2015-07-29
      • Published Date: 2016-01-25

      Catalog

        Journal of Semiconductors © 2017 All Rights Reserved   京ICP备05085259号-2

        /

        DownLoad:  Full-Size Img  PowerPoint
        Return
        Return