| Citation: |
Mei Lin, Yixu Xu, Jianhua Zhang, Shunqing Wu, Zizhong Zhu. Hybrid functional calculations on the band gap bowing parameters of InxGa1-xN[J]. Journal of Semiconductors, 2016, 37(4): 042001. doi: 10.1088/1674-4926/37/4/042001
****
M Lin, Y X Xu, J H Zhang, S Q Wu, Z Z Zhu. Hybrid functional calculations on the band gap bowing parameters of InxGa1-xN[J]. J. Semicond., 2016, 37(4): 042001. doi: 10.1088/1674-4926/37/4/042001.
|
Hybrid functional calculations on the band gap bowing parameters of InxGa1-xN
DOI: 10.1088/1674-4926/37/4/042001
More Information
-
Abstract
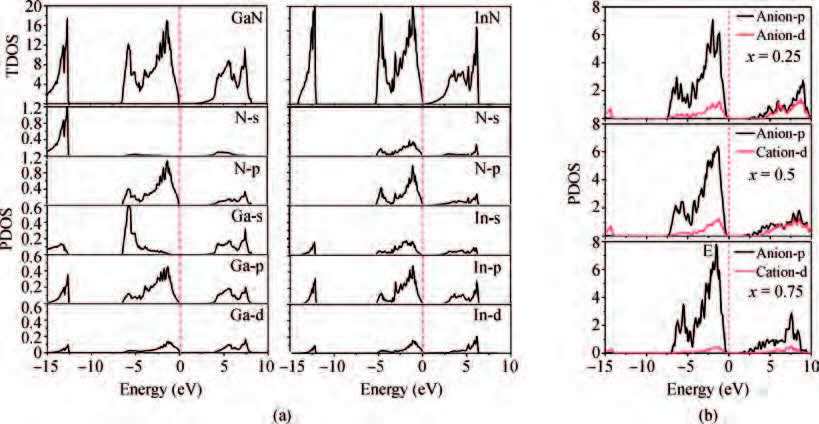
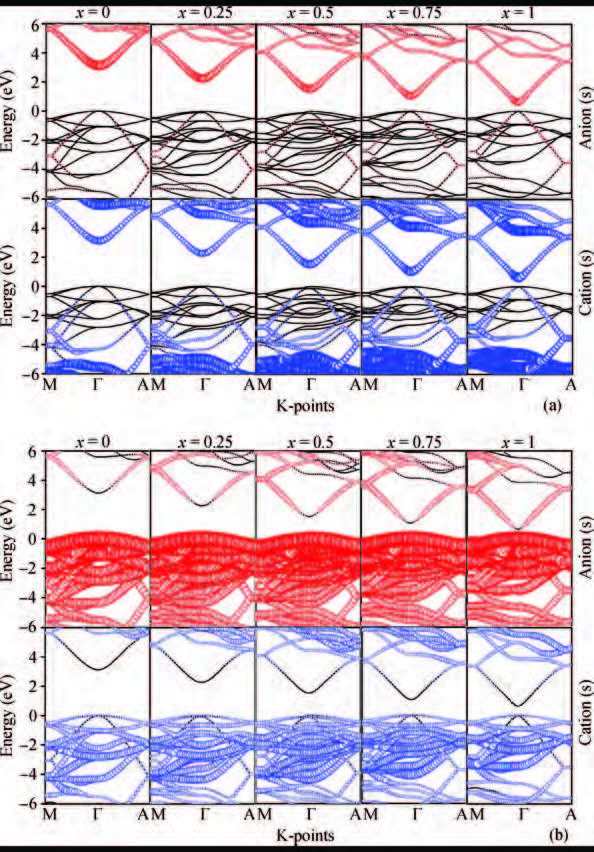
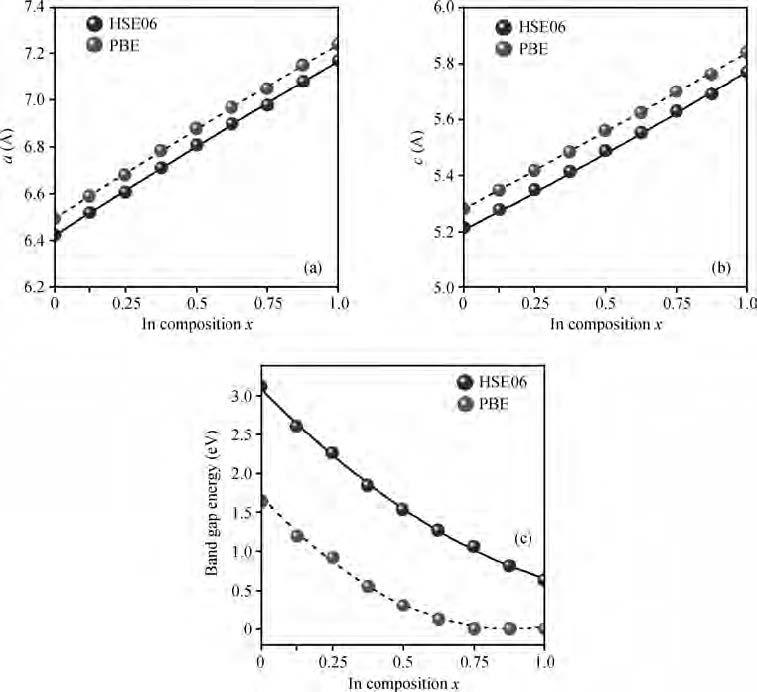
The electronic band structures and band gap bowing parameters of InxGa1-xN are studied by the first-principles method based on the density functional theory. Calculations by employing both the Heyd-Scuseria-Ernzerh of hybrid functional (HSE06) and the Perdew-Burke-Ernzerhof (PBE) one are performed. We found that the theoretical band gap bowing parameter is dependent significantly on the calculation method, especially on the exchange-correlation functional employed in the DFT calculations. The band gap of InxGa1-xN alloy decreases considerably when the In constituent x increases. It is the interactions of s-s and p-p orbitals between anions and cations that play significant roles in formatting the band gaps bowing. In general, the HSE06 hybrid functional could provide a good alternative to the PBE functional in calculating the band gap bowing parameters.-
Keywords:
- InxGa1-xN,
- bowing parameters,
- HSE06 functional,
- PBE functional
-
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] -
Proportional views





 DownLoad:
DownLoad: