| Citation: |
Yao Fei, Tianshu Yang, Zhaofeng Li, Wen Liu, Xiaodong Wang, Wanhua Zheng, Fuhua Yang. Design of the low-loss waveguide coil for interferometric integrated optic gyroscopes[J]. Journal of Semiconductors, 2017, 38(4): 044009. doi: 10.1088/1674-4926/38/4/044009
****
Y Fei, T S Yang, Z F Li, W Liu, X D Wang, W H Zheng, F H Yang. Design of the low-loss waveguide coil for interferometric integrated optic gyroscopes[J]. J. Semicond., 2017, 38(4): 044009. doi: 10.1088/1674-4926/38/4/044009.
|
Design of the low-loss waveguide coil for interferometric integrated optic gyroscopes
DOI: 10.1088/1674-4926/38/4/044009
More Information
-
Abstract
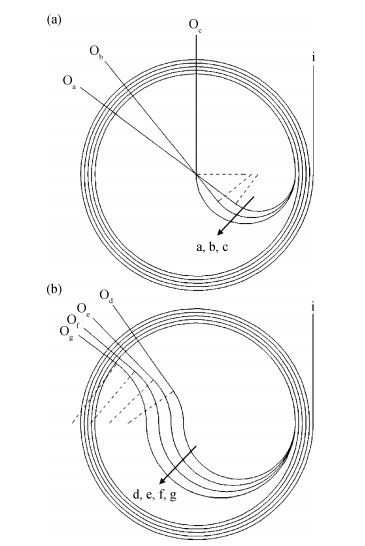
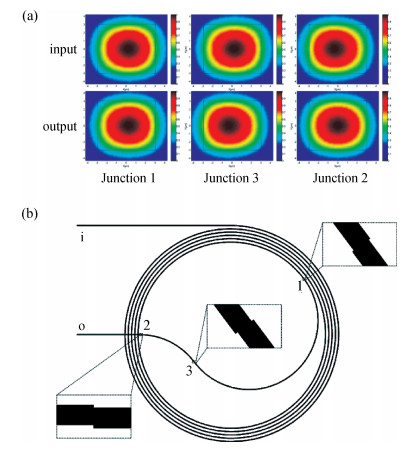
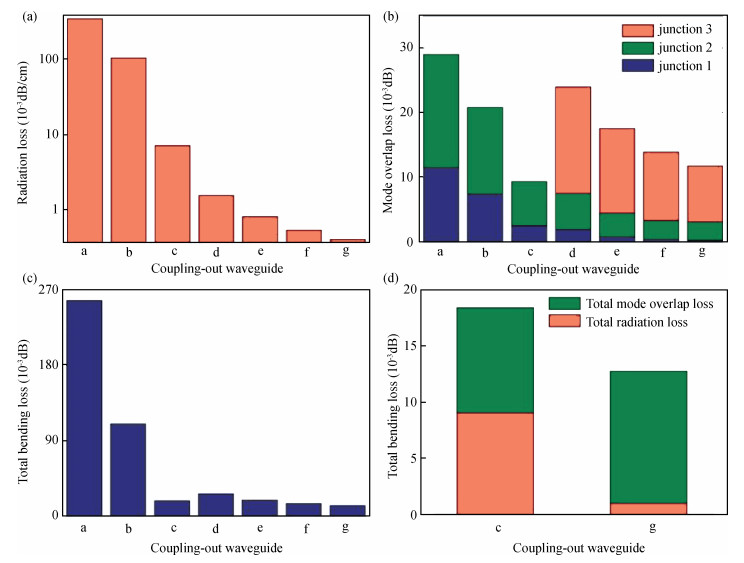
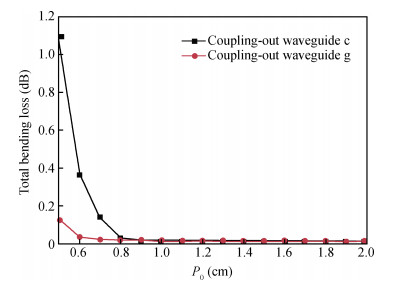
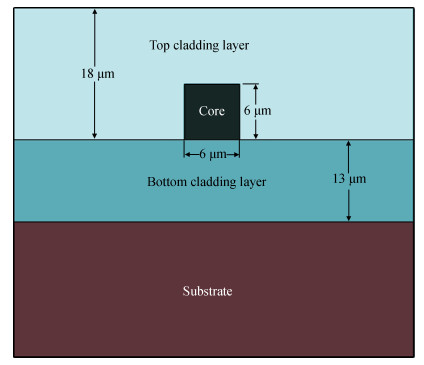
With the development of manufacturing technology, the propagation loss of the planar waveguide is getting lower and lower, and the shot-noise-limited sensitivity of an IIOG will be greatly improved. When the propagation loss is getting lower, improper coupling-out waveguide in the waveguide coil may lead to non-ignorable bending loss and crosstalk because of the small radius of curvature and X-junction. In this paper, different coupling-out waveguides have been designed. After calculation and optimization by the beam propagation method, we found the proper coupling-out waveguide having relatively low propagation loss, which can improve the sensitivity of the IIOG.-
Keywords:
- gyroscopes,
- Sagnac effect,
- planar waveguides,
- integrated optics
-
References
[1] Li C, Zhang C, Song N, et al. Polarization-maintaining fiber loop with double optical length and its application to fiber optic gyroscope. Chin Opt Lett, 2011, 9(2): 020604 doi: 10.3788/COL[2] Mi J, Zhang C, Li Z, et al. Bias phase and light power dependence of the random walk coefficient of fiber optic gyroscope. Chin Opt Lett, 2006, 4(7): 379 http://en.cnki.com.cn/Article_en/CJFDTOTAL-GXKB200607003.htm[3] Yang Y, Zhang W, Ma J, et al. Low cost, practical, all-digital open-loop fiber-optic gyroscope. Chin Opt Lett, 2003, 1(10): 567 https://www.researchgate.net/publication/249341747_Low_cost_practical_all-digital_open-loop_fiber-optic_gyroscope[4] Zheng Y, Ren Y, An P, et al. Wide dynamic range experiments on a resonator fiber optic gyro based on closed-loop frequency locking technique. Chin Opt Lett, 2015, 13(2): 020601 doi: 10.3788/COL[5] Sagnac G. Lèher lumineux dèontrèpar l'effet du vent relatif d'èher dans un interfèomère en rotation uniforme. CR Acad Sci, 1913, 157: 708[6] Mottier P, Pouteau P. Solid state optical gyrometer integrated on silicon. Electron Lett, 1997, 33(23): 1975 doi: 10.1049/el:19971319[7] Ciminelli C, Dell'Olio F, Armenise M N. High-Q spiral resonator for optical gyroscope applications: numerical and experimental investigation. IEEE Photon J, 2012, 4(5): 1844 doi: 10.1109/JPHOT.2012.2218098[8] Ning L, Guo L J, Kong M, et al. Waveguide-type optical passive ring resonator gyro using frequency modulation spectroscopy technique. J Semicond, 2014, 35(12): 124008 doi: 10.1088/1674-4926/35/12/124008[9] Lee H, Chen T, Li J, et al. Ultra-low-loss optical delay line on a silicon chip. Nat Commun, 2012, 3: 867 doi: 10.1038/ncomms1876[10] Bauters J F, Heck M J, John D D, et al. Planar waveguides with less than 0. 1 dB/m propagation loss fabricated with wafer bonding. Opt Express, 2011, 19(24): 24090[11] Srinivasan S, Moreira R, Blumenthal D, et al. Design of integrated hybrid silicon waveguide optical gyroscope. Opt Express, 2014, 22(21): 24988 doi: 10.1364/OE.22.024988[12] Zhang T, Liu H, Qian Y, et al. Power loss of X-junction in solid state optical gyrometer simulated by beam propagation method. Proc SPIE, 2005, 5644: 479 doi: 10.1117/12.570300[13] Gundavarapu S, Huffman T, Belt M, et al. Integrated ultra-low-loss silicon nitride waveguide coil for optical gyroscopes. Opt Fiber Commun Conf, 2016[14] Feit M, Fleck J Jr. Light propagation in graded-index optical fibers. Appl Opt, 1978, 17(24): 3990 doi: 10.1364/AO.17.003990[15] Scarmozzino R, Gopinath A, Pregla R, et al. Numerical techniques for modeling guided-wave photonic devices. IEEE J Sel Top Quantum Electron, 2000, 6(1): 150 doi: 10.1109/2944.826883[16] Yevick D. A guide to electric field propagation techniques for guided-wave optics. Opt Quantum Electron, 1994, 26(3): S185 doi: 10.1007/BF00384672[17] Lefèvre H C. The fiber-optic gyroscope. Artech Hourse, 1992[18] Neumann E G. Curved dielectric optical waveguides with reduced transition losses. IEE Proceedings H: Microwaves Optics and Antennas, 1982[19] Kitoh T, Takato N, Yasu M, et al. Bending loss reduction in silica-based waveguides by using lateral offsets. J Lightw Technol, 1995, 13(4): 555 doi: 10.1109/50.372465[20] Ciminelli C, Dell'Olio F, Campanella C E, et al. Photonic technologies for angular velocity sensing. Adv Opt Photon, 2010, 2(3): 370 doi: 10.1364/AOP.2.000370[21] López-Higuera J M. Handbook of optical fibre sensing technology. Wiley, 2002 -
Proportional views





 DownLoad:
DownLoad: