1. Introduction

Phase locked loop (PLL) is a critical sub-system for many applications such as wireless transceiver, high speed analog-to-digital converters (ADC) and system-on-chip (SoC) circuits^[1–4]. In the nano-scale CMOS process, the performances of analog PLLs are limited by the poor intrinsic device gain, decreased supply voltage and increased leakage current. Therefore, all-digital PLLs (ADPLL) have been designed to take advantage of the new process and to improve the PLL performances. The ADPLLs that employ a time-to-digital converter (TDC) for phase detecting need a high resolution and wide-linear range TDC in order to achieve low in-band phase noise^[5–7]. But a TDC with high resolution and wide-linear range is area consuming and power hungry. Compared with the TDC based ADPLL, the bang-bang phase/frequency detector (BBPFD) based ADPLLs (BBPLLs) which use only 1-bit phase-detecting output have advantages of simplicity, low power and low area^[8–17].

However, the conventional BBPLL has the issue of a long locked time because the BBPFD recognizes only the polarity of the phase error and has no magnitude information of phase error for phase locking. Consequently, traditional BBPLLs are still unsuitable for the frequency hopping systems and fast recovering applications, which require a short locked time of the PLL. Several techniques have been proposed to reduce the locked time of the BBPLL^[13–17]. These techniques are based on the idea of coarse frequency searching or dynamically calibrating loop band-width, according to the detecting phase error. In Refs. [13–15], a multi-level-output BBPFD (MLO-BBPFD)^[13,14] or a hybrid TDC-BBPFD^[15] is proposed to accelerate the locking process of the BBPLL. The MLO-BBPFD and TDC-BBPFD have the advantage of multi-bits phase error output, which contains the magnitude of the phase error for fast frequency acquisition. However, the MLO-BBPFD and TDC-BBPFD greatly complicate the circuits design and increase the power and area. In Ref. [14], a frequency search algorithm is used for DCO coarse frequency control words setting, thus it accelerates the frequency searching process. However, the frequency search time and accuracy are sensitive to process-voltage-temperature (PVT) variations as the DCO gain is changed due to PVT variations. The fixed searching time of the frequency search process is unavoidable and wasted even when the frequency jump is very small. In Ref. [16], a modified bang-bang algorithm based on a finite state machine (FSM) is adopted to monitor the phase error and increase the locking speed. However, with the FSM method the BBPLL still needs a long time in the frequency acquisition process. Besides, there is an unstable damping effect during the locking process. Thus, extra locking time is needed to make the BBPLL settling down.

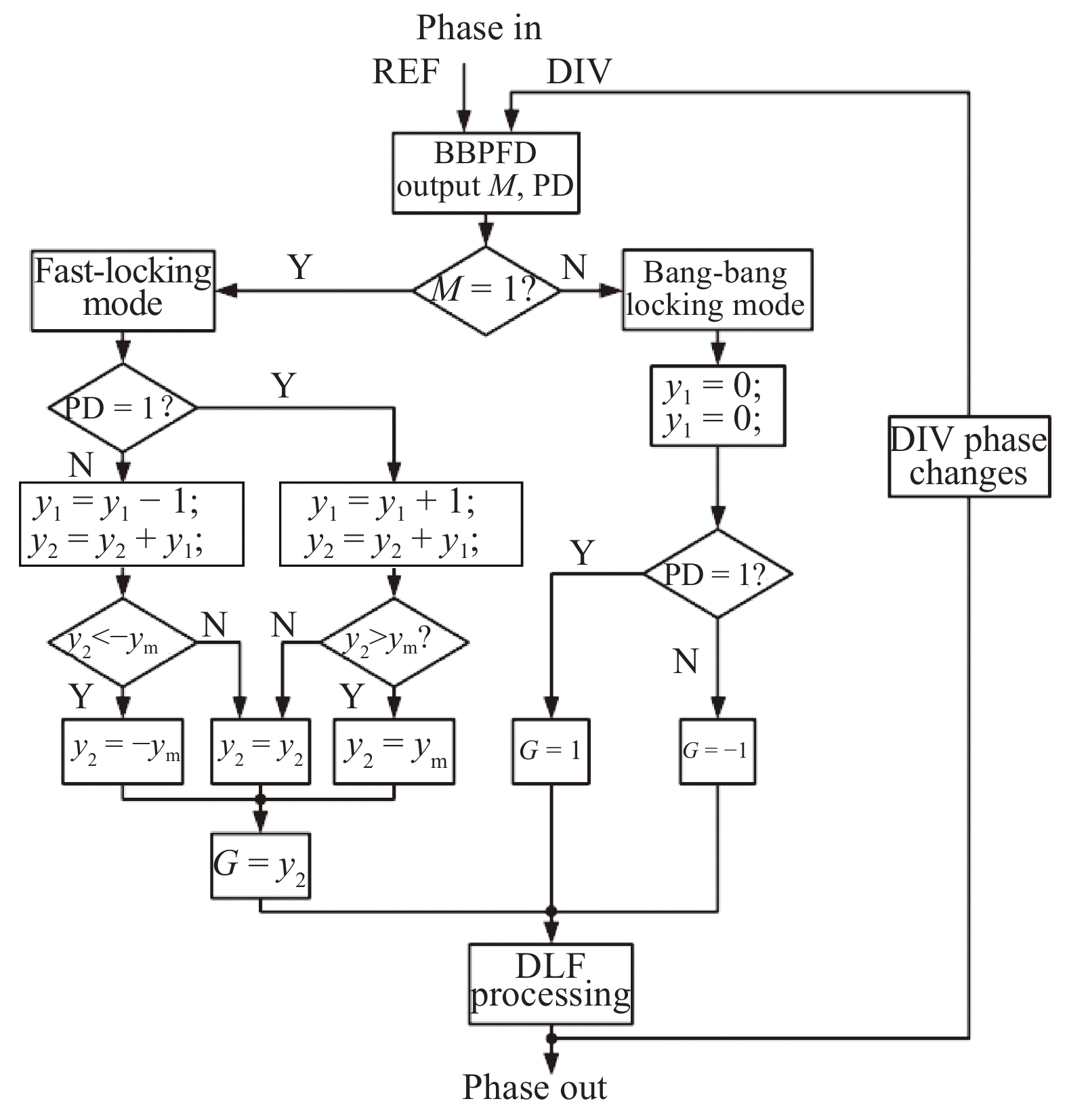
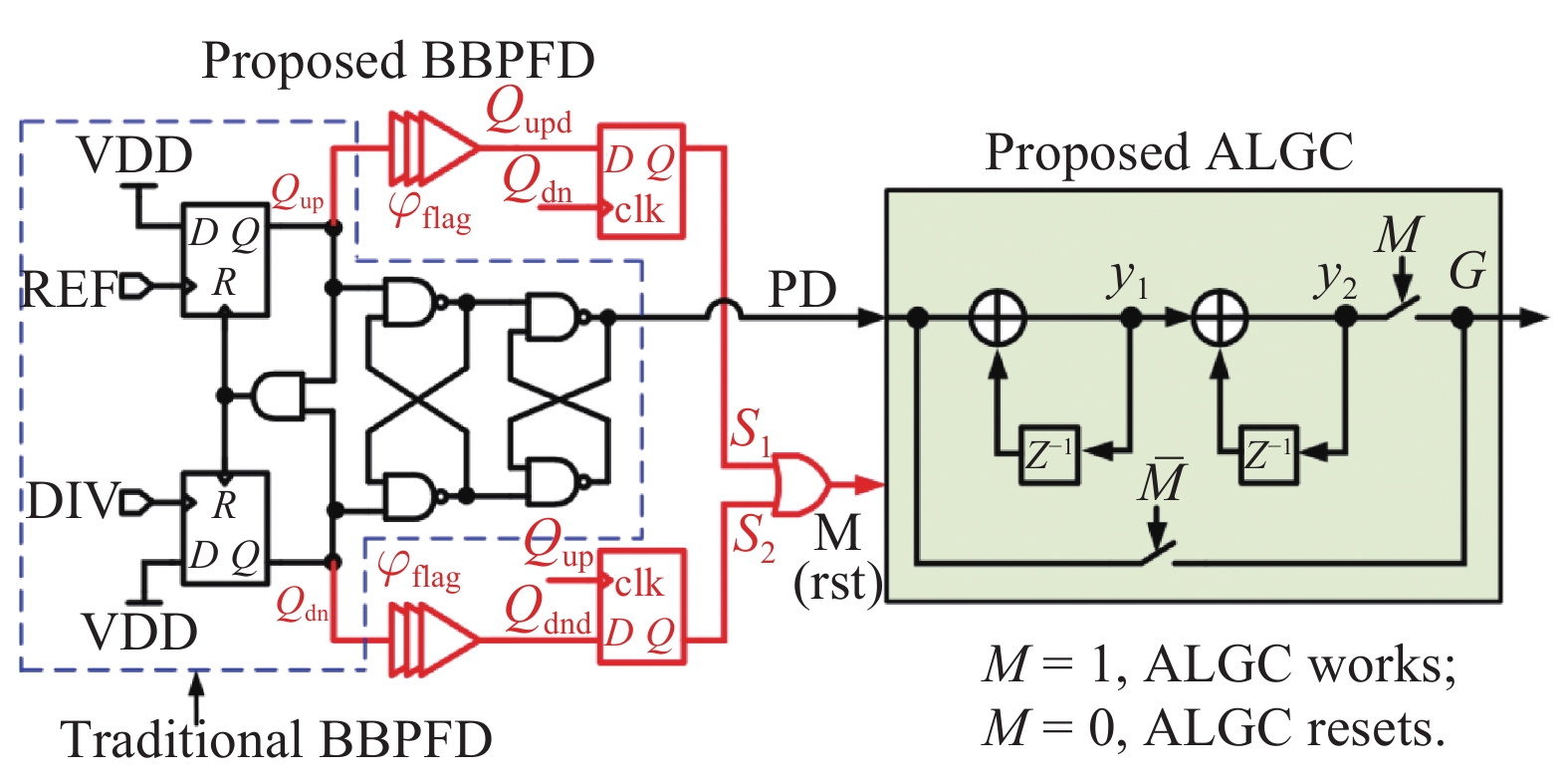
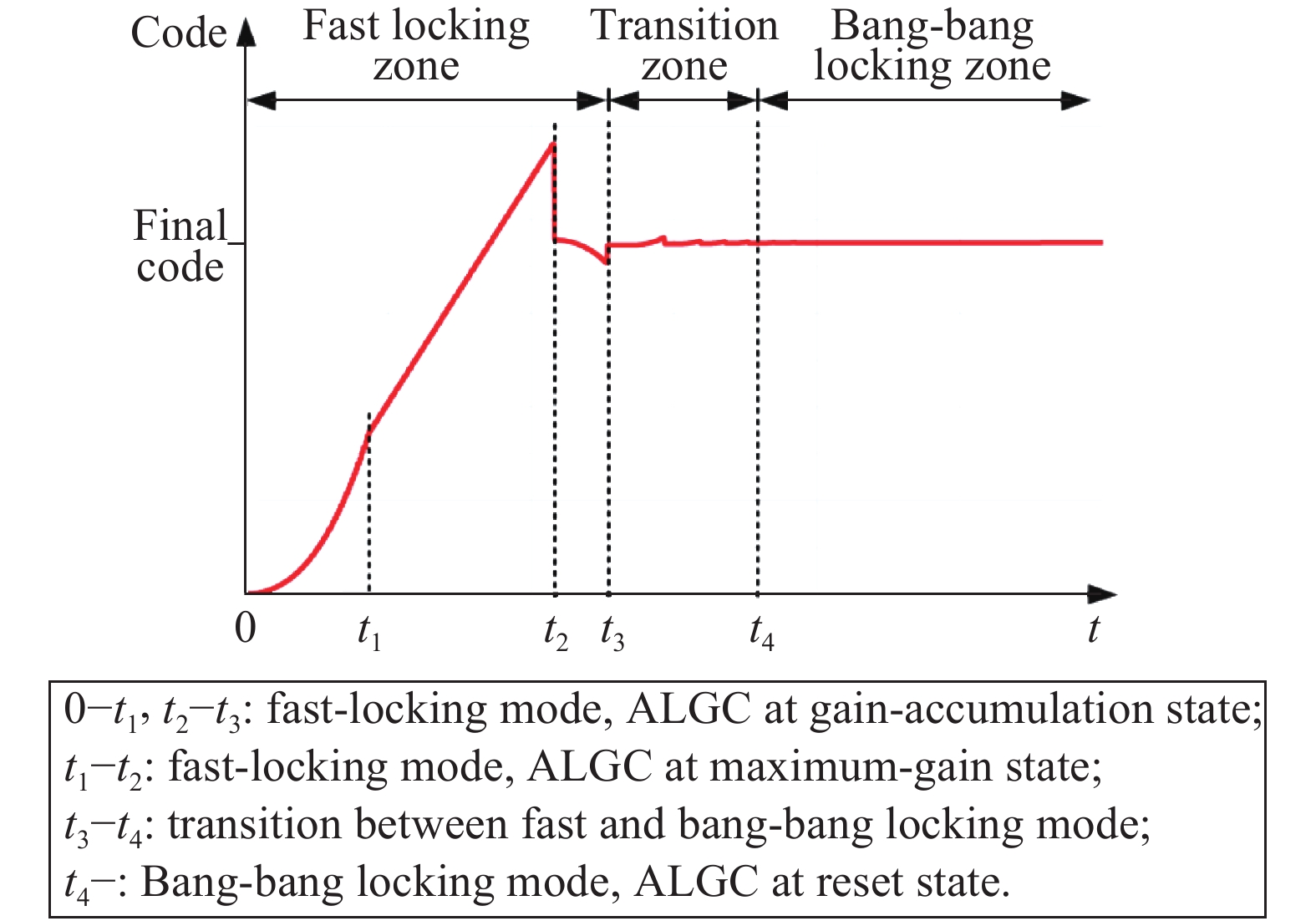
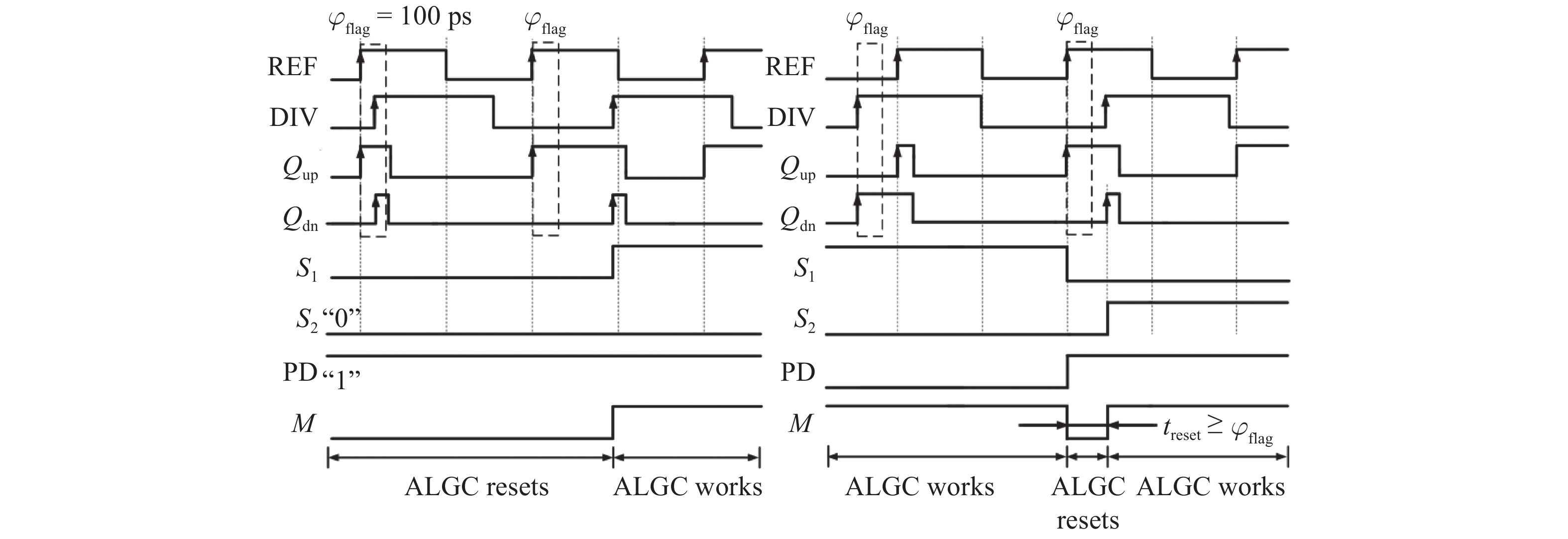
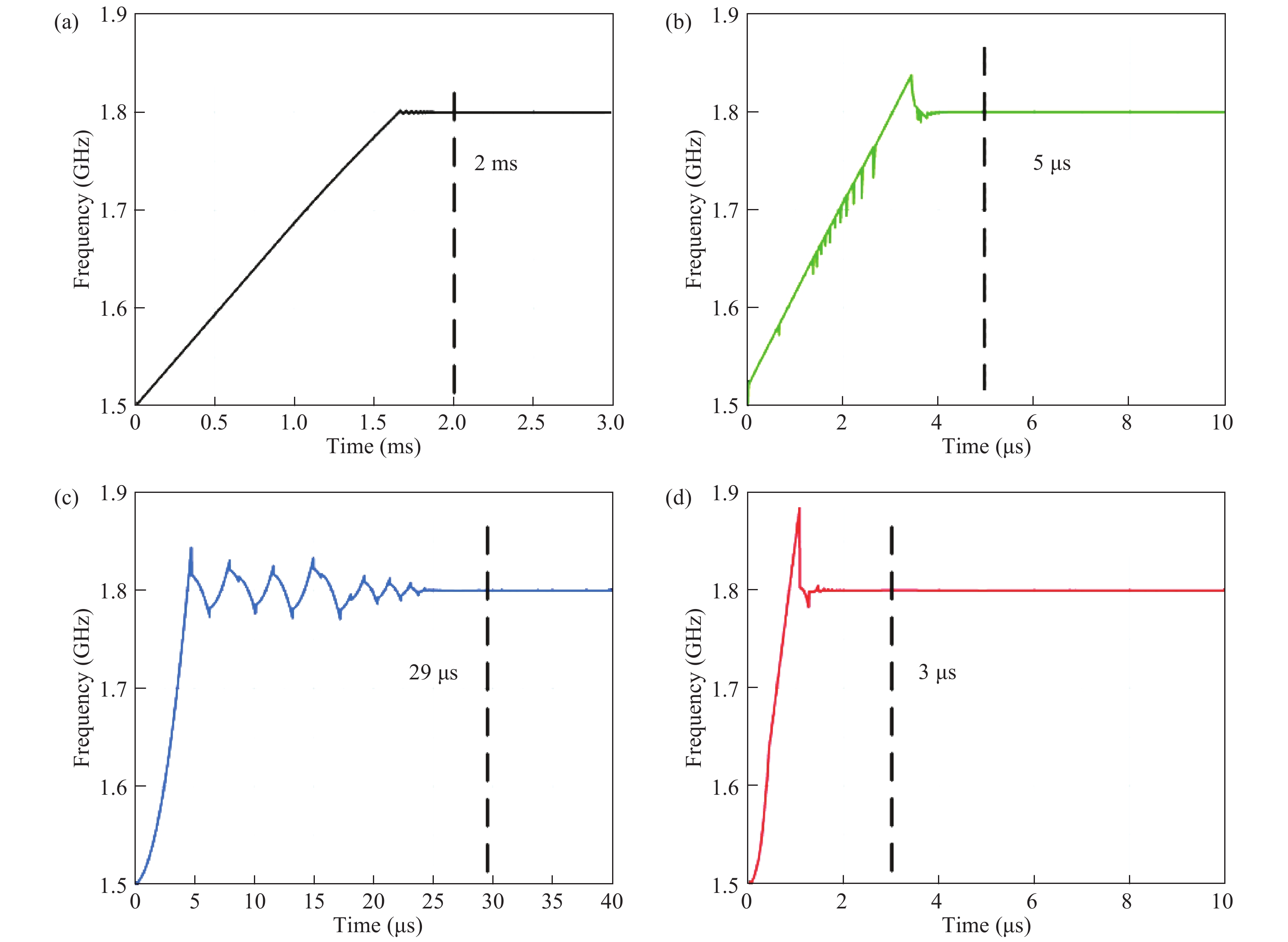
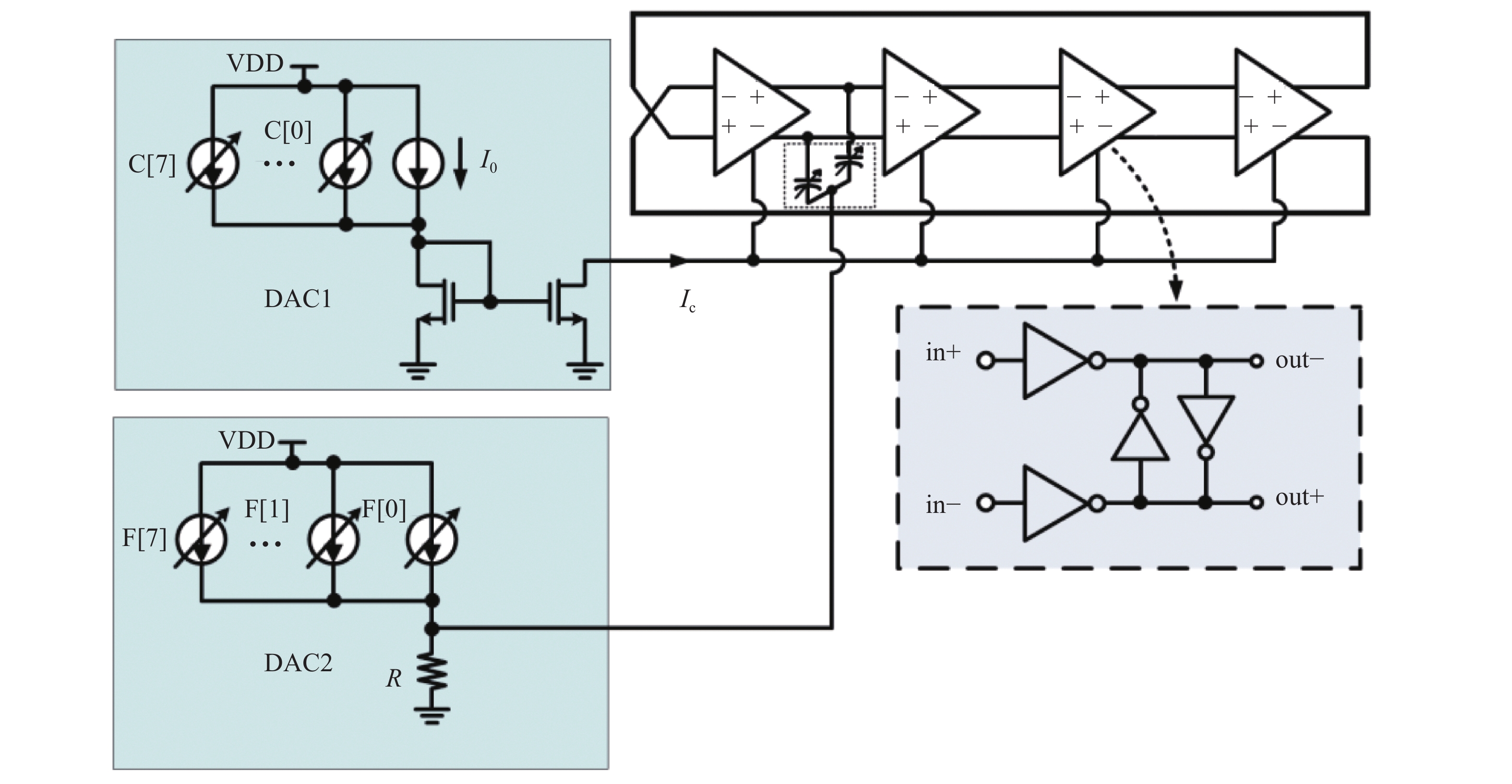
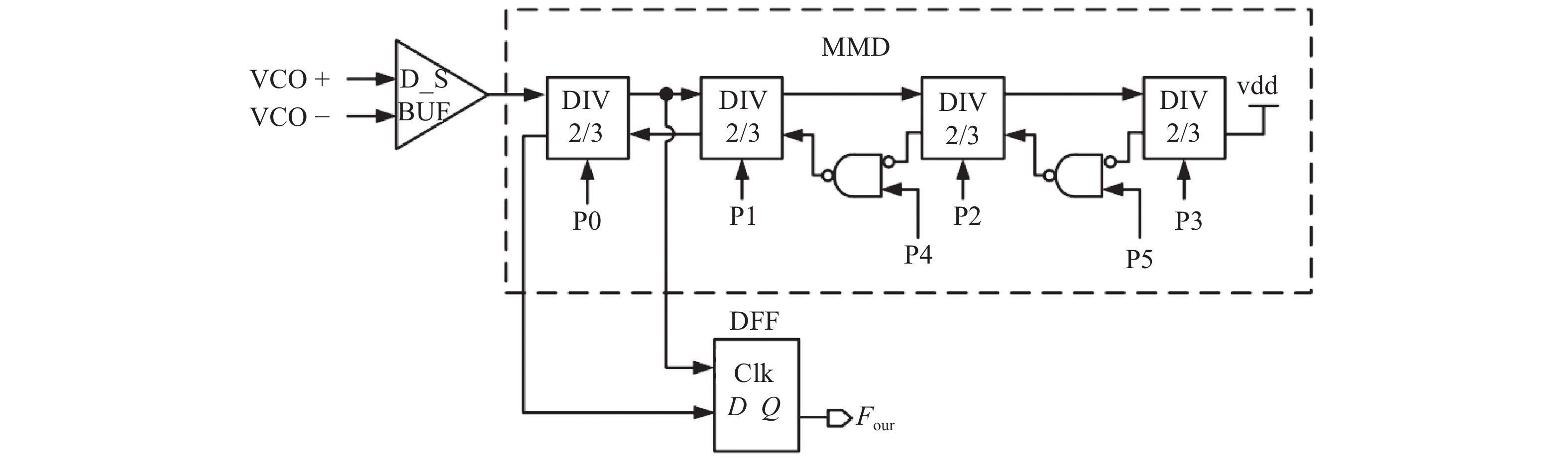
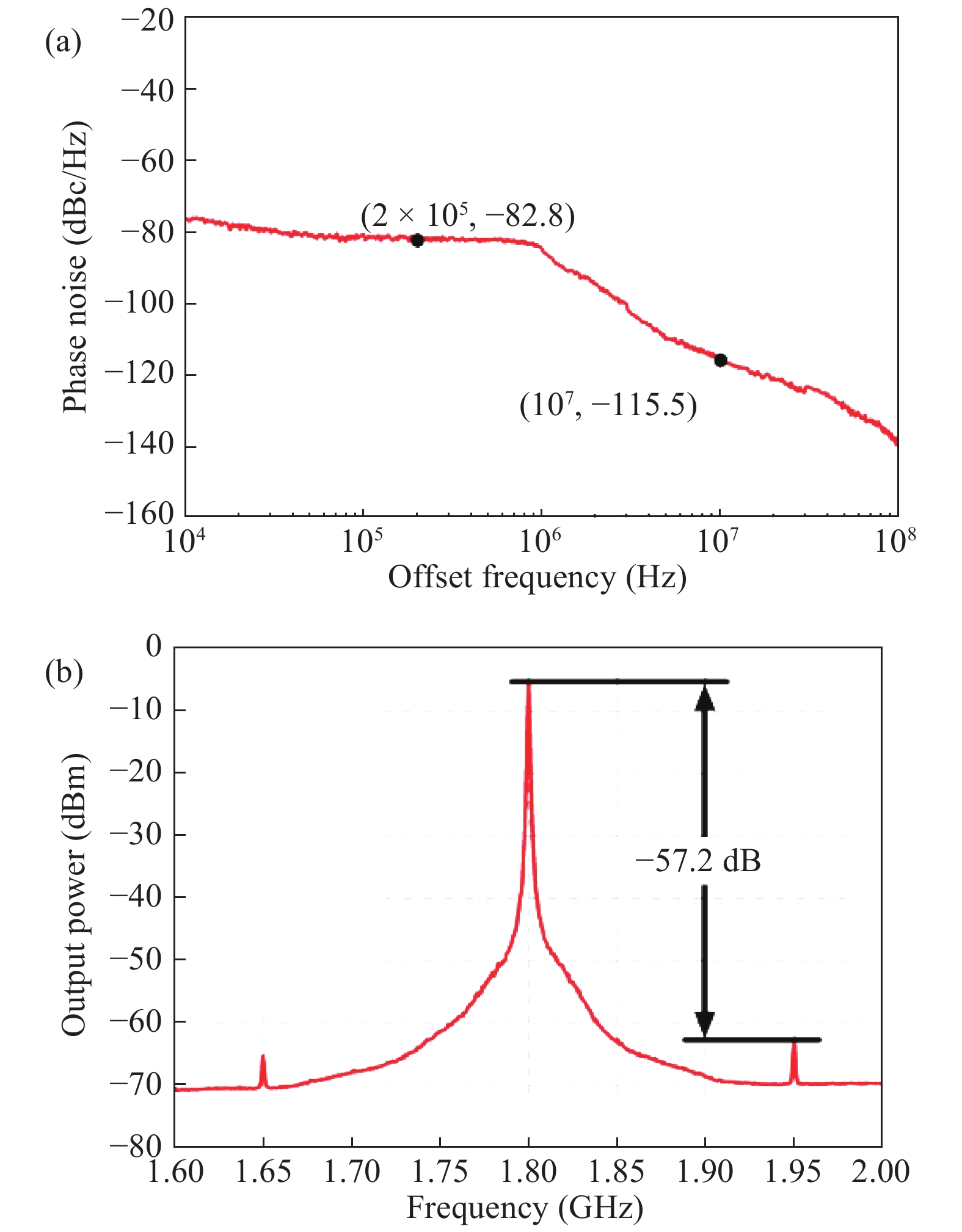
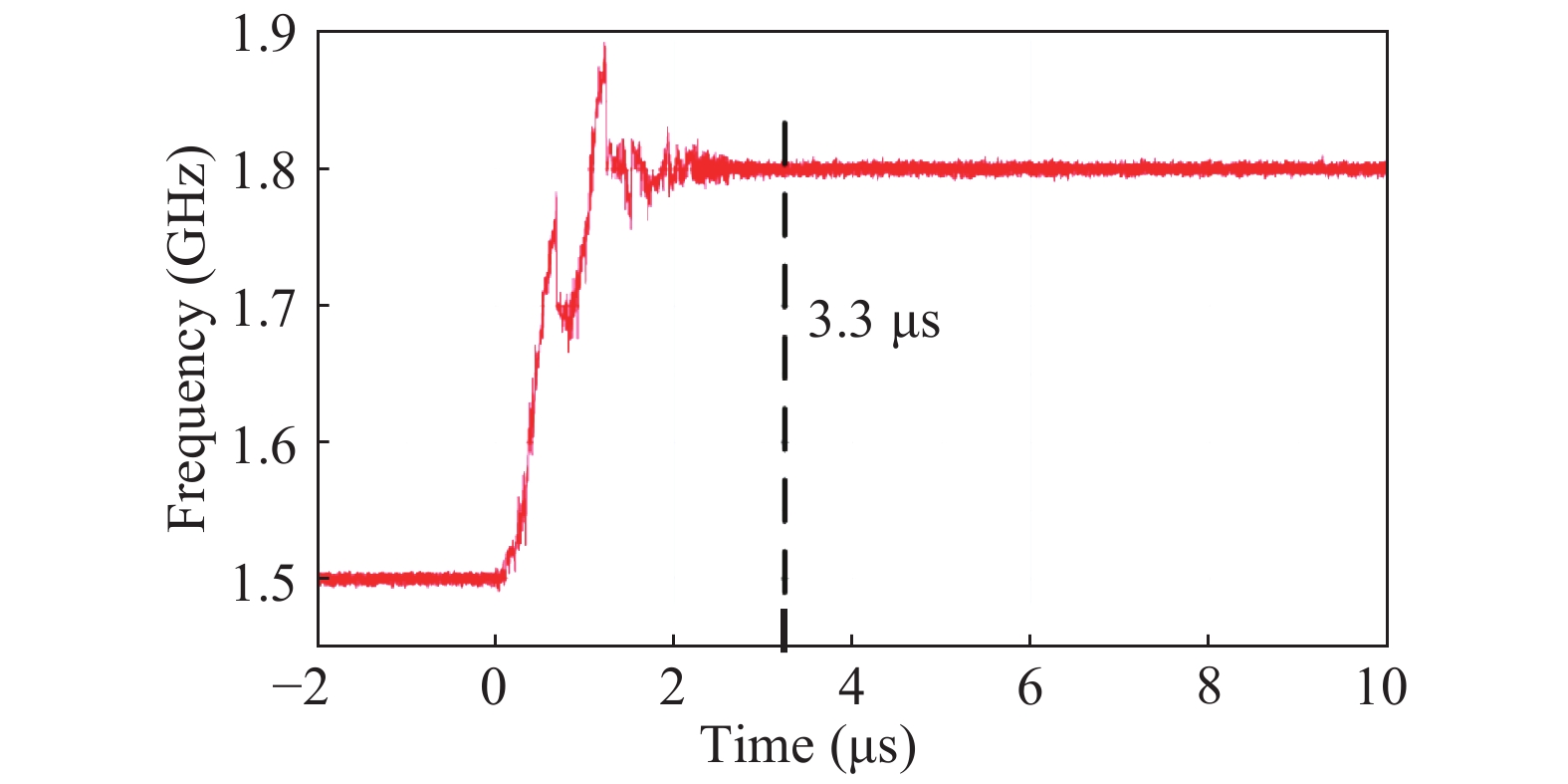
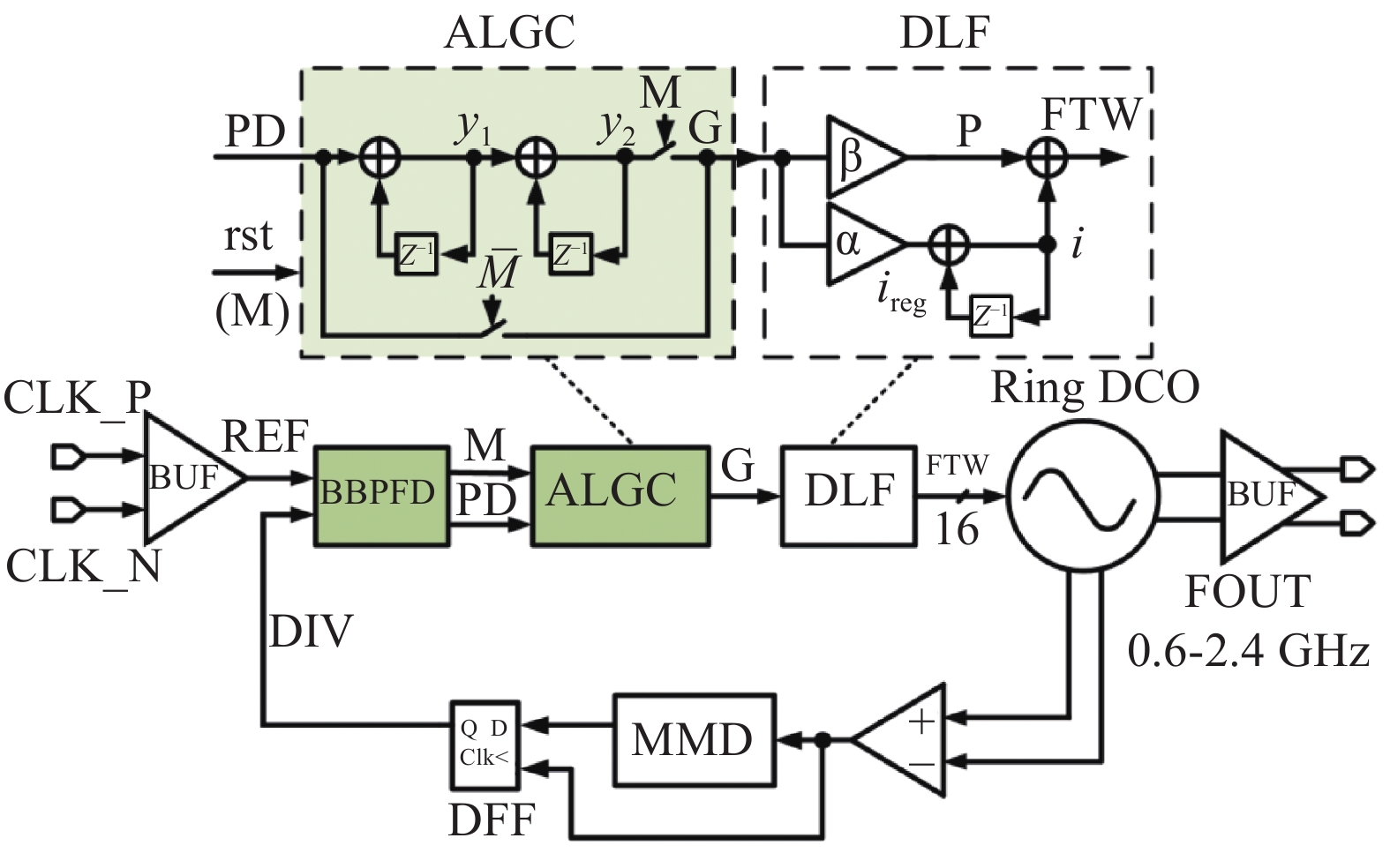
This paper proposes a fast-locking BBPLL. A novel adaptive loop gain controller (ALGC) is proposed to reduce the locked time of the BBPLL. A novel bang-bang phase/frequency detector (BBPFD) with adaptive mode selective circuits is proposed to select the locking mode of the BBPLL during the locking process. Based on the detected results of the BBPFD, the ALGC can dynamically calibrate the gain of the digital loop filter for the fast-locking procedure. Therefore, the BBPLL can achieve a fast locking speed with low area and low power.

2. Architecture and operating procedure of the fast-locking BBPLL

Fig. 1 shows the architecture of the proposed fast-locking BBPLL. It consists of a 4-stage differential ring oscillator based digitally controlled oscillator (DCO), a multi-module divider (MMD) with a retiming dynamic flip-flop (DFF), a proposed BBPFD with adaptive mode selective circuits, an ALGC block and a digital loop filter (DLF), a differential-to-single end buffer, input buffer and output buffer. The ALGC is used for adaptive loop gain control during the locking process of the BBPLL. The proposed BBPFD is used to not only output the 1-bit phase error signal “PD” but also to adaptively select the fast-locking and normal bang-bang locking mode of the BBPLL by generating the control signal “M”.

Fig. 2 shows the working flow chart of the BBPLL. The BBPLL works as follows: besides the 1-bit signal of the phase error polarity “PD”, the BBPFD also outputs another 1-bit flag signal “M” (Fig. 1), which indicates whether the phase error between the “REF” and “DIV” is larger or smaller than flag phase φ_flag.

When M = 1, it means the phase error is larger than φ_flag, the loop is switched to work in the fast-locking mode. In this mode, ALGC works to control the loop gain. The parameters y₁, y₂ and G in the ALGC (Fig. 1) are calculated as follows:

${y_1} = {y_1} \pm 1,$

(1)

${y_2} = \left\{\,\,\,\,\,\,{\begin{split}&{{y_{\rm{m}}}{\rm{,}}\qquad\quad\;{\rm{if}}\;\;{y_2} + {y_1} > {y_{\rm{m}}}},\\&{{y_2} + {y_1}{\rm{,}}\;\;\;\;\;\;\;{\rm{if}}\;\; - {{\rm{y}}_{\rm{m}}} \leqslant {y_2} + {y_1} \leqslant {y_{\rm{m}}}},\\&{ - {y_{\rm{m}}}{\rm{,}}\;\quad\quad\,\,{\rm{if}}\;\;{y_2} + {y_1} < - {y_{\rm{m}}}},\end{split}}\right.$

(2)

$G = {y_2},$

(3)

where the “±” sign in Eq. (1) indicates the adjusting direction of the phase, which depends on the polarity of phase error “PD”. y₁, y₂ are signed numbers, which can be larger or smaller than 0. y_m is the maximum value of the y₂, which is limited by the bits number in digital circuits. So, if the BBPFD output M = 1 and “PD” is a consecutive series of “1” or “0”, the overall loop gain of the BBPLL will be accumulated to a large value to speed up the locking process.

When M = 0, which means the phase error is smaller than the φ_flag, the loop is switched to work in the normal bang-bang locking mode. In this mode, the integrator in the ALGC is reset, that is, y₁ = 0, y₂ = 0, and bypassed by “M” (Fig. 1). If the polarity of the phase error PD = 1, then G = 1; if the PD = 0, then G = −1, and the BBPLL works as a conventional BBPLL.

3. Circuits design and implementations

3.1 Proposed ALGC and BBPFD with adaptive mode selective circuits

Fig. 3 shows the detailed schematic of the proposed ALGC and BBPFD blocks. The ALGC is implemented as a two-order integrator with a bypassing branch circuit. The novel BBPFD is designed as a conventional BBPFD with adaptive mode selective circuits (the red parts in Fig. 3). As shown in the figure, the traditional PFD and latches realize the traditional BBPFD. The “Q_up” and “Q_dn” represent the phase error, and the “PD” represents the polarity of the phase error. A delay line is inserted between “Q_up/Q_dn” and a dynamic flip-flop (DFF) to implement the flag phase φ_flag. The delay signal Q_upd/Q_dnd is then triggered by the “Q_dn/Q_up” to generate the dedicated sub-flag-signal “S₁/S₂”. The flag signal “M” is then generated by the “OR” operation of S₁ and S₂. Thus, “M” indicates whether the magnitude of the phase error is larger than φ_flag or not. Compared with the conventional BBPFD, only a few gates are added in the BBPFD. Thus, the proposed BBPFD with adaptive-mode-selective circuits is realized with little area and power penalties.

The ALGC work together with the proposed BBPFD for the adaptive loop gain control. Fig. 4 shows the timing diagrams of the BBPFD with different phase error situations. As shown in the figure, “M” can be used to adaptively select the locking modes of the BBPLL based on the phase error. If the phase error is larger than φ_flag, M = 1, the BBPLL works at the fast locking mode; if the phase error is smaller than φ_flag, M = 0, the BBPLL works at the normal bang-bang phase locking mode.

Fig. 4(b) shows the situation where PD changes during the fast-locking process of the BBPLL. Therefore, in order to avoid an unstable damping effect, it is critical that ALGC is reset, whenever the PD is changed. As shown in the figure, the proposed BBPFD has the merit that M will be switched to 0 with a reset timing-window no smaller than φ_flag, when PD is switched from 0 to 1 or from 1 to 0. Therefore, M can also be used as the “reset” signal for the ALGC, which alleviates the extra circuits for the adaptive “reset” signal of the ALGC. According to the simulation, the flag phase is set to be φ_flag = 100 ps to achieve a short locked time and have enough reset timing-window for the ALGC.

To better understand the locking process of the fast-locking BBPLL with the proposed ALGC and BBPFD, Fig. 5 shows the simulated transient output code of the DLF. When the phase error between REF and DIV is larger than φ_flag, m consecutive “1” or “0” are generated at the “PD” of the BBPFD. While y₂ does not reach the maximal/minimal edge of y_m/−y_m, the ALGC works as a two-order integrator for loop gain accumulation. The ALGC is in the gain-accumulation state, y₁, y₂ start to accumulate as follows:

${y_1}[m] = \pm m,$

(4)

${y_2}[m] = \pm \left( {1 + 2 + \cdot \cdot \cdot + m} \right) = \pm \frac{{{m^2} + m}}{2},$

(5)

$G[m] = {y_2}[m].$

(6)

The output codes of the DLF proportional path p and integral path i are expressed as follows:

$p = \beta G = \pm \beta \frac{{{m^2} + m}}{2},$

(7)

$i = i + \alpha G = i \pm \alpha \frac{{{m^2} + m}}{2},$

(8)

where β and α are the basic proportional gain and integral gain in the DLF, respectively, and the “±” sign depends on the polarity of phase error “PD”. It take “+” for the case of 0→t₁, and “–” for the case of t₂→t₃ in Fig. 5. Eqs. (4) – (8) show that, when in the gain-accumulation state, the ALGC keeps accumulating, and the loop gain of the BBPLL increases with a trend of a hyperbolic function. Therefore, the locking speed of the BBPLL is accelerated with an increasing loop gain, until y₂ reaches the maximum value y_m at t₁.

At time t₁, although y₂ has reached the maximal value of y_m, the phase error is still large, so the BBPFD still outputs M = 1. Therefore, during time t₁→t₂, ALGC stop accumulating and y₂ remains at y_m. The ALGC is in the maximum-gain state. Parameters of ALGC and DLF in this state are expressed as:

${y_1} = {y_1},$

(9)

${y_2} = \pm {y_{\rm{m}}},$

(10)

$G = \pm {y_{\rm{m}}},$

(11)

$p = \beta G = \pm \beta {y_{\rm{m}}},$

(12)

$i = i + \alpha G = i \pm \alpha {y_{\rm{m}}}.$

(13)

Eqs. (9) – (13) show that, in this state, the DLF proportional and integral gain is maximal. The locking process of BBPLL is accelerated at a maximum-gain speed, with a bang-bang behavior, until the polarity of the phase error “PD” changes.

When “PD” is changed, if the phase error is still larger than φ_flag with an opposite direction, it corresponds to the case from t₂→t₃. The BBPFD outputs M = 0 firstly to reset the ALGC (Fig. 4(b)), then BBPFD will output M = 1 again and ALGC will be turned to the gain-accumulation state for the fast phase error reduction.

When “PD” is changed, if the phase error is smaller than φ_flag, which corresponds to the case at t₃, the BBPLL is switched to a normal bang-bang phase locking mode. However, as there is still a frequency error, the phase error will keep accumulating until it becomes larger than φ_flag again. Then the BBPFD will switch the loop to the fast-locking mode again. The transitions between the fast-locking and bang-bang phase locking modes repeat, until there is no frequency error and the phase error is smaller than φ_flag at time t₄.

At time t₄, the phase error is smaller than φ_flag, BBPFD output M = 0 and switches the BBPLL to a normal bang-bang locking mode. In the normal bang-bang locking mode, the ALGC is in a reset-state. The integrators in the ALGC will be reset and “bypassed” by “M”. Parameters of the ALGC and DLF are as follows:

${y_1} = 0,$

(14)

${y_2} = 0,$

(15)

$G = \pm 1,$

(16)

$p = \beta G = \pm \beta ,$

(17)

$i = i + \alpha G = i \pm \alpha .$

(18)

In the normal bang-bang locking mode from t₄, BBPLL works as a conventional one until the phase is finally locked. As the phase error between the “REF” and “DIV” is now smaller than φ_flag, the BBPLL will spend only a short locking time in the normal bang-bang locking mode.

Fig. 6 shows the simulated frequency locking line of the conventional BBPLL^[12], fast-locking BBPLL with the technique of MLO-BBPFD in Refs. [13, 14], the technique of the FSM algorithm in Ref. [16] and with the ALGC in our design, respectively. The same parameters are used for the simulation: reference frequency is 150 MHz, DCO frequency tuning gain is 80 kHz/LSB, and the DLF proportional gain and integral gain are β = 1/2 and α = 1/64, respectively. The frequency jump is set to be 300 MHz. As is shown in Fig. 6(a), the conventional BBPLL has a slow locking process. Thus the settled time is about 1.9 ms. Fig. 6(b) shows the MLO-BBPFD based fast-locking BBPLL. A 9-bits MLO-BBPFD is adopted here for simulation. As the MLO-BBPFD converts the phase error to the multi-bits digital code, it works like a TDC-based ADPLL. Thus the phase locking time is shortened to 5 μs. However, the area and power consumption of the MLO-BBPFD is as large as a typical TDC, which degrades the simple and low-power merits of the BBPFD. Fig. 6(c) shows the frequency locking line of the FSM-algorithm based fast-locking BBPLL. It shows that, with the FSM-algorithm method in Ref. [16], a relatively long time is still needed in the frequency acquisition process, thus the locked time is 29 μs. Fig. 6(d) is the frequency lock line of the proposed fast-locking BBPLL. The locked time is 3 μs with the proposed ALGC techniques.

3.2 DCO

Fig. 7 shows a schematic of the proposed DCO. It is composed of a 4-stage ring oscillator. The delay stage of the DCO is implemented by 2 current controlled inverters and an inverter-based latch to realize a fully differential structure. Currents and the load capacitance of the delay stages are used for the frequency tuning of the DCO. A 7-bit binary-encoded digital-to-analog converter (DAC1) is adopted to transfer the digital codes into the currents for the delay cell of the DCO as coarse frequency tuning. The DCO frequency-resolution is critical for the jitter and spur performances of the DCO, as the quantization noise will increase the in-band phase noise and the reference spurs of the ADPLL. Therefore, two MOS-varactors operating at the accumulated-mode are used for the fine tuning of the DCO. Another 7-bit DAC (DAC2) is used to supply the tuning voltage for the varactors. Based on the post-layout simulation, the frequency resolution of the DCO is 80 kHz/LSB. The overall tuning range of the VCO is from 0.6 to 2.5 GHz.

3.3 MMD

Fig. 8 presents the schematic of the MMD. It mainly consists of 4 stages of divde-by-2/3 divider cell (DIV-2/3). A differential-to-single-end buffer (D_S BUF) is used to turn the differential VCO signal into a single-end clock. It reduces the load capacitance of the DCO and isolates the DCO from the MMD to avoid the interference from MMD. A retiming DFF is used to retime the output of the MMD by the output of the first DIV-2/3 cell. It eliminates the noise accumulation in the rest stages of the DIV-2/3 cells in the MMD, thus reducing the in-band noise of the FLBBPLL. Using the output signal of the first DIV-2/3 cell for the retiming clock also relaxes the operating frequency of the retiming DFF, thus saving the power. The MMD has a divider-ratio ranging from 4 to 31. The post-layout simulation shows that the MMD can operate at the highest input frequency of 3 GHz at all PVT-corners, which is sufficient to cover the DCO output frequency.

4. Measurement results

The proposed fast-locking BBPLL is fabricated in a 65 nm CMOS process. The die micrograph is shown in Fig. 9. The core area of the BBPLL is 0.022 mm². The output frequency range of the fast-locking BBPLL is from 0.6 to 2.4 GHz with a 150-MHz reference clock. When operating at 1.8 GHz, the fast-locking BBPLL consumes power of 3.1 mW from a 0.9-V supply voltage, excluding the output buffer. The measured phase noise and spectrum at 1.8-GHz frequency are shown in Fig. 10(a) and (b), respectively. The in-band phase noise at 200-kHz frequency offset is −82.8 dBc/Hz, and the out-of-band phase noise at 10-MHz frequency offset is −115.5 dBc/Hz. The root-mean-square (RMS) jitter integrated from 10 kHz to 100 MHz is 10.3 ps. The reference spur is −57.2 dB.

A high speed oscilloscope is used to measure the frequency locking response of the locking process. Fig. 11 shows the measured frequency locking line of the fast-locking BBPLL from 1.5 to 1.8 GHz. As shown in the figure, the measured frequency locked time is 3.3 μs with a frequency jump of 300 MHz. The glitches in the locked state of the locking line are due to the limited sampling rate of the oscilloscope in the measurement. The normalized locked time is 1.1 μs per 100 MHz frequency jump.

Table 1 gives the performance summary of this design and comparisons with the previous fast-locking BBPLLs. In order to fairly compare the performances of the fast-locking BBPLLs, considering the power, output jitter and the normalized lock time, a figure-of-merit (FoM) of the fast-locking PLLs that is derived in Ref. [18] is adopted, which is defined as follows:

${\rm FoM} = 10\log \left[ {{{\left(\frac{{{t_{\rm{l}}}}}{{1{\rm s}}}\right)}^2} \times {{\left(\frac{{{\sigma _{\rm{t}}}}}{{1{\rm s}}}\right)}^2}\times \left(\frac{P}{{1\,{\rm mW}}}\right)} \right],$

(19)

where t_l is the normalized frequency locked time, σ_t is the RMS jitter and P is power consumption.

5. Conclusion

A fast-locking BBPLL with novel ALGC was proposed to increase the locking speed of the BBPLL. A novel BBPFD was proposed to adaptively select the working mode of the BBPLL. The measured results showed that the BBPLL operates at a frequency range of 0.6 – 2.4 GHz. The power consumption at 1.8 GHz is 3.1 mW. With the proposed techniques, the fast-locking BBPLL achieved a normalized locked time of 1.1 μs @ 100 MHz frequency jump. The proposed fast-locking BBPLL achieved an FoM of −334.0 dB.