| Citation: |
Chengying Chen, Hongyi Zhang. A 0.6-V, 69-dB subthreshold sigma–delta modulator[J]. Journal of Semiconductors, 2018, 39(12): 125004. doi: 10.1088/1674-4926/39/12/125004
****
C Y Chen, H Y Zhang, A 0.6-V, 69-dB subthreshold sigma–delta modulator[J]. J. Semicond., 2018, 39(12): 125004. doi: 10.1088/1674-4926/39/12/125004.
|
A 0.6-V, 69-dB subthreshold sigma–delta modulator
DOI: 10.1088/1674-4926/39/12/125004
More Information
-
Abstract
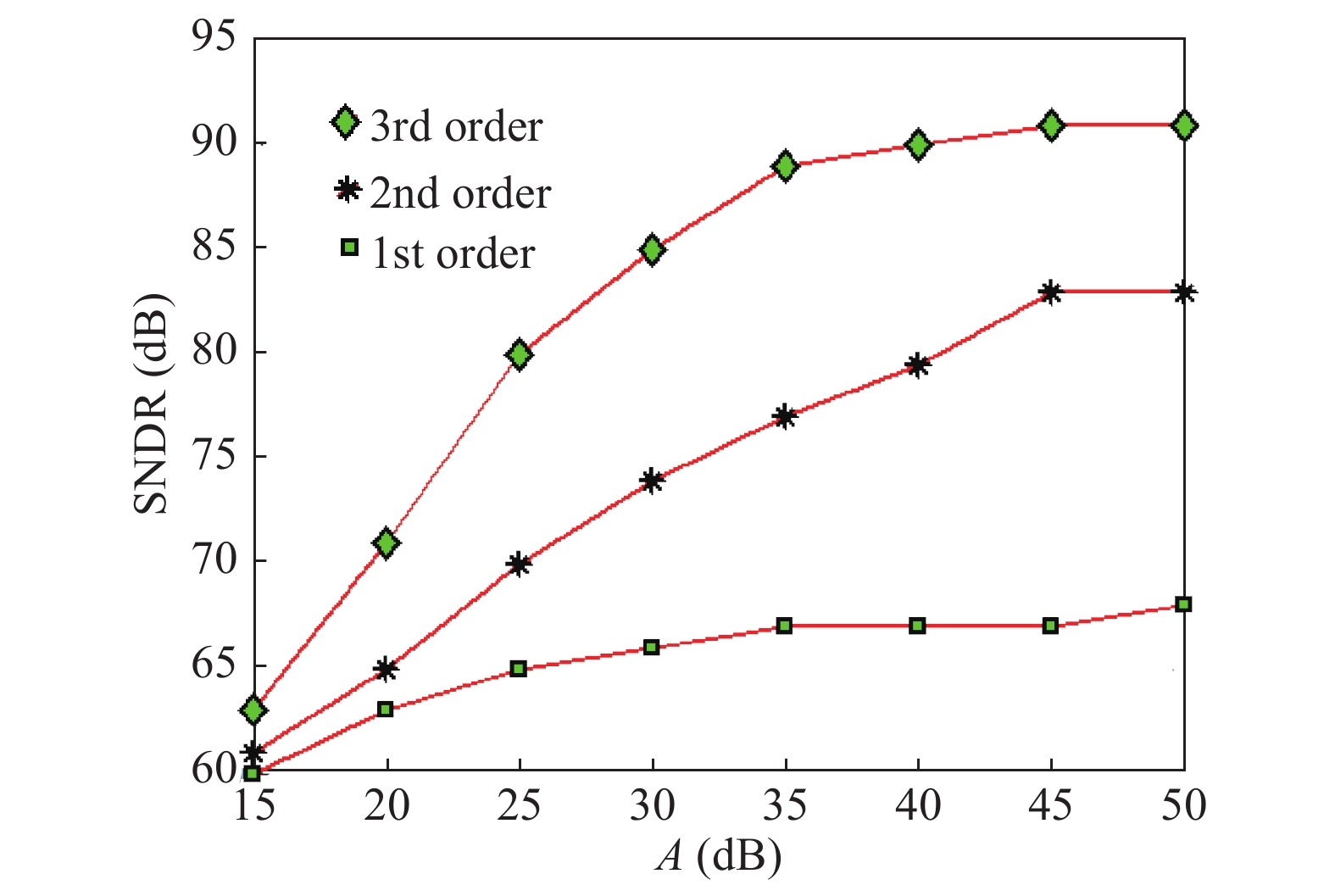
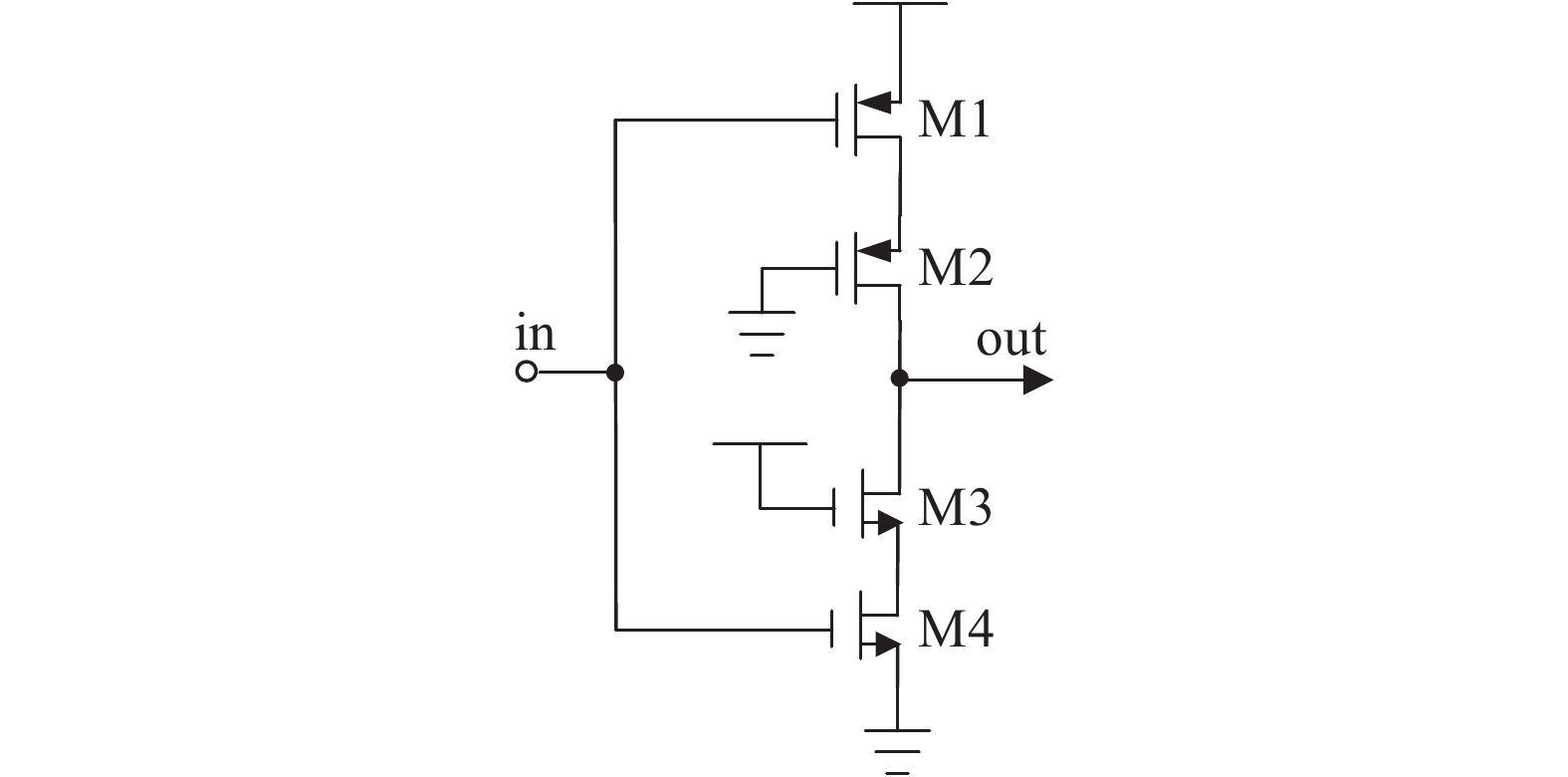
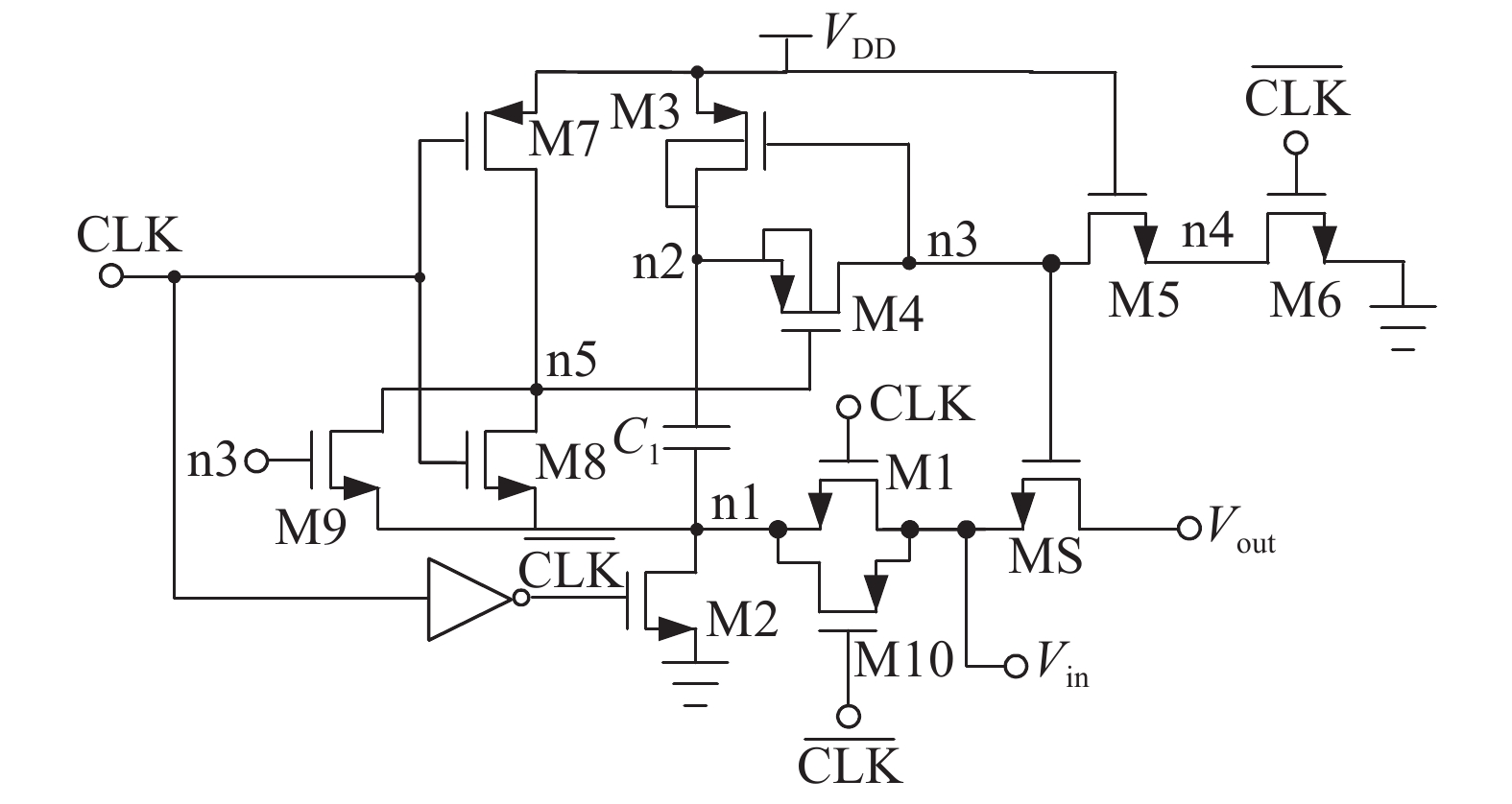
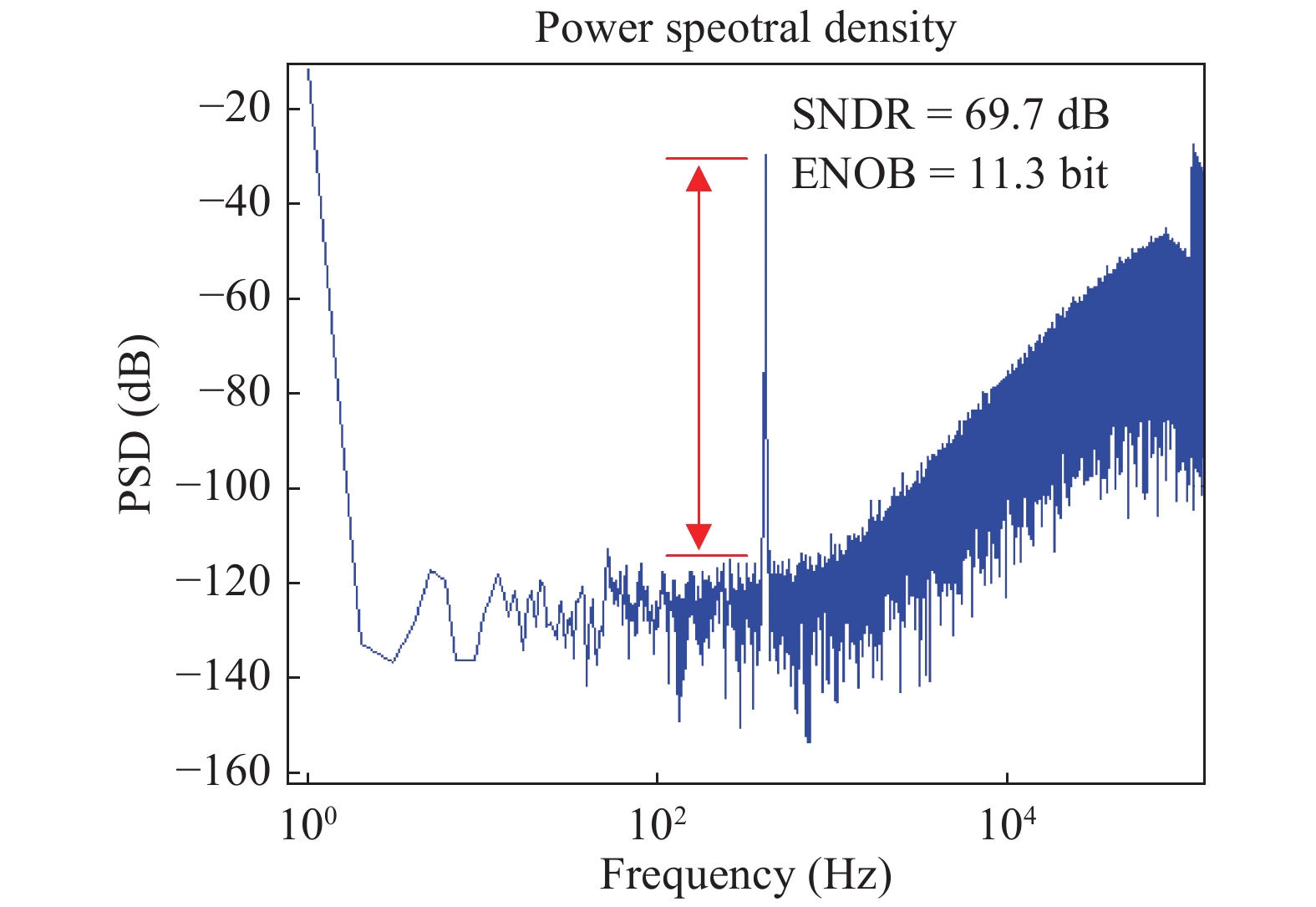
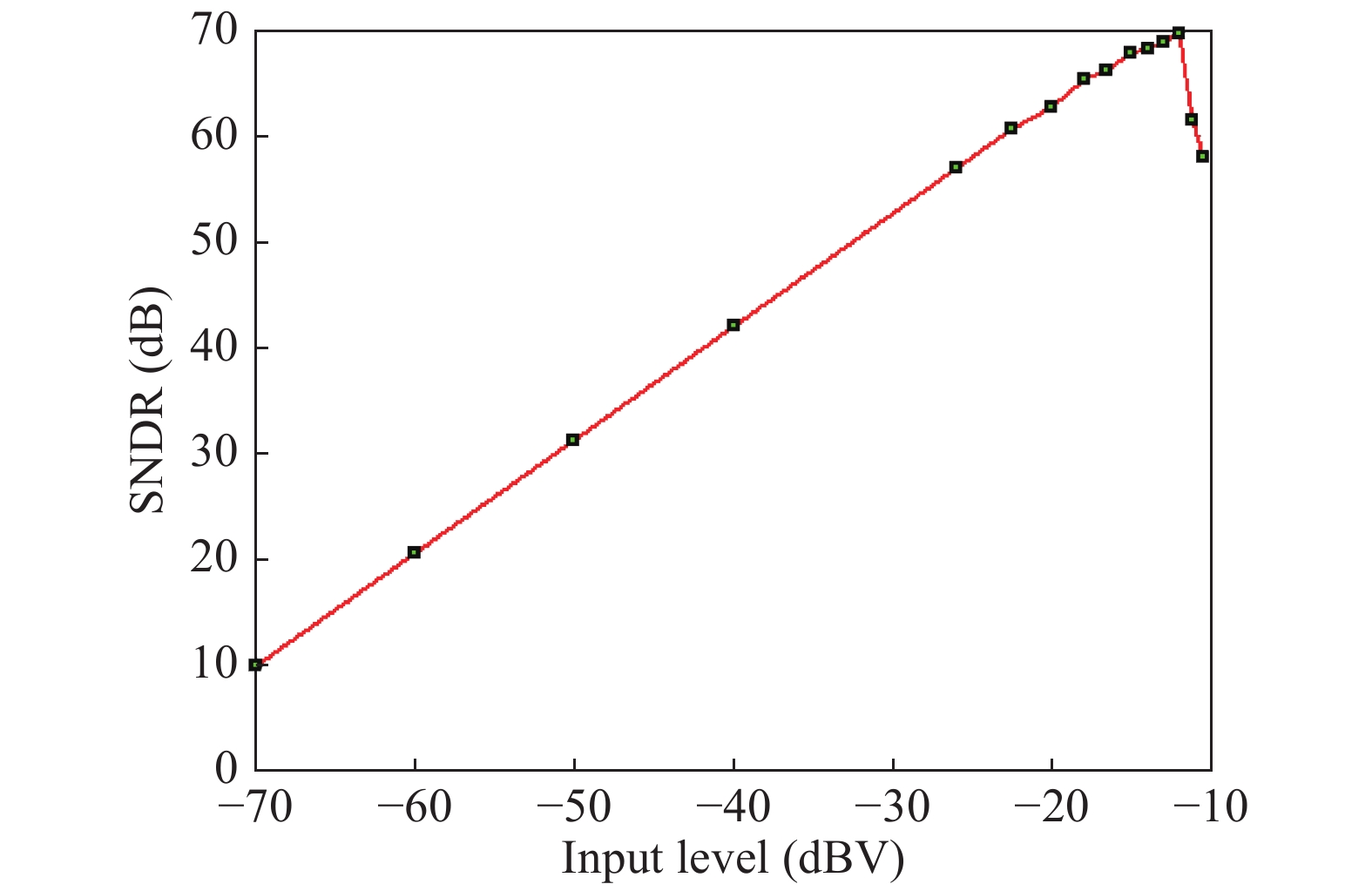
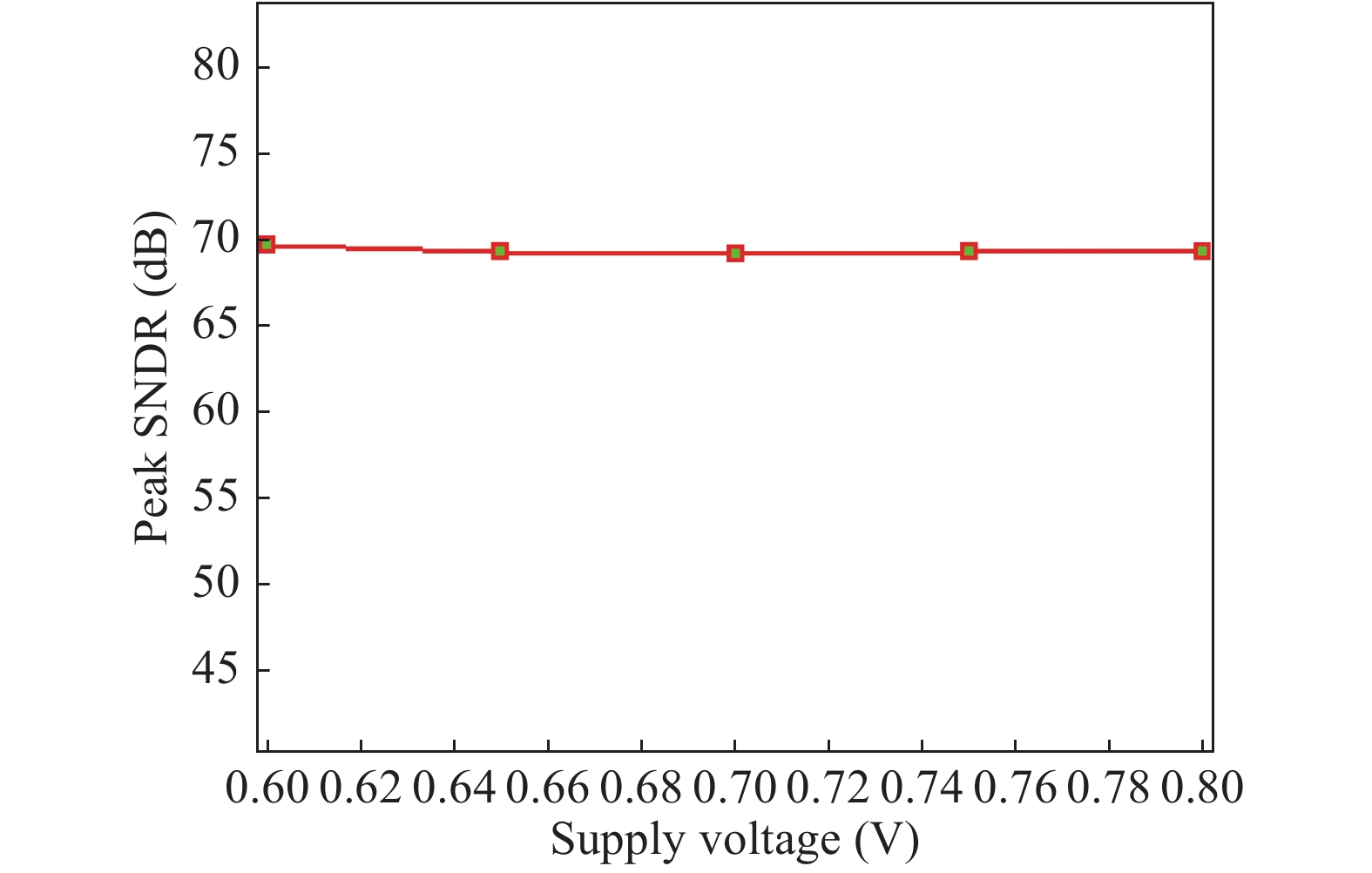
In this paper a 0.6 V, 14 bit/500 Hz subthreshold inverter-based sigma–delta modulator is proposed. In the first integrator of the modulator, a bootstrap switch is used to accomplish accurate signal sampling. Without a transconductor operational amplifier (OTA), the sigma–delta modulator adopts a cascode inverter in the subthreshold region to save power consumption. The modulator is fabricated with a 0.13 μm CMOS mixed-signal process. The experiment results show that with the 0.6 V power supply it achieves a maximum SNDR of 69.7 dB and an ENOB of 11.3 bit, respectively, but only consumes 5.07 μw power dissipation.-
Keywords:
- subthreshold,
- sigma–delta modulator,
- inverter,
- bootstrap switch
-
References
[1] Wang Y C, Ke K R, W H Q, et al. A low power low noise analog front end for portable healthcare system. J Semicond, 2015, 36(10): 105008 doi: 10.1088/1674-4926/36/10/105008[2] Mao Y Q, Gao T Q, Xu X D, et al. A fully integrated CMOS super-regenerative wake-up receiver for EEG applications. J Semicond, 2016, 37(9): 095001 doi: 10.1088/1674-4926/37/9/095001[3] Xiao G L, Qin Y L, Xu W L, et al. Demonstration of a fully differential VGA chip with small THD for ECG acquisition system. J Semicond, 2015, 36(10): 105005 doi: 10.1088/1674-4926/36/10/105005[4] Panigrahi A, Parhi A. A 0.5-V body driven pseudo-differential OTA for low voltage and low power applications. IEEE India Conference (INDICON), 2015: 1[5] Zhao X K, Song Z, Chi B Y. A 60-dB DR PGA with DC-offset calibration for short-distance wireless receiver. IEEE International Symposium on VLSI design, Automation and Test (VLSI-DAT), 2015: 1[6] Hsu T F, Huang C P, Chao I J, et al. A first-order low distortion sigma–delta modulator using split DWA technique and SAR quantizer. IEEE International Symposium on VLSI design, Automation and Test (VLSI-DAT), 2015: 13[7] Chae Y, Lee I, Han G. A 0.7-V 36-μW 85dB-DR audio sigma–delta modulator using class-C inverter. IEEE Solid-State Circuits Conference, 2008: 490[8] Abiri E, Pournoori N. A 0.5-V 17 μW second-order delta-sigma modulator based on a self-biased digital inverter in 0.13 μm CMOS. J Basic ad Appl Sci Res, 2012, 2(4): 3476[9] Michel F, Steyaert M. A 250 mV 7.5 μW 61 dB SNDR SC sigma–delta Modulator using near-threshold-voltage-biased inverter amplifier in 130 nm CMOS. IEEE J Solid-State Circuits, 2012, 47(3): 709 doi: 10.1109/JSSC.2011.2179732[10] Yang Y, Yang Y, Lu L, et al. Inverter-based second-order sigma–delta modulator for smart sensor. Electron Lett, 2013, 49(7): 31[11] Chae Y, Han G. Low voltage, low power, inverter-based switch-capacitor delta-sigma modulator. IEEE J Solid-State Circuits, 2009, 44(2): 458 doi: 10.1109/JSSC.2008.2010973[12] Singh A, Rawat V, Agarwal A. Low-power 10-bit 100 MS/s pipelined ADC in digital CMOS technology. IET Circuit, Devices & Systems, 2017, 11(6): 589[13] Xu W G, Gao Y F, Liu X D, et al. A 18 mW 12 bit 50 MS/s SHA-less pipelined ADC. IEEE 12th International Conference on ASIC (ASICON), 2017: 776[14] Chao F B, Chen Y Z, Cao Y F, et al. A proved dither-injection method for memory effect in double sampling pipelined ADC. IEEE 12th International Conference on ASIC (ASICON), 2017: 754[15] Sarma V, Jacob N, Sahoo B, et al. A 250-MHz pipelined ADC-based fs/4 noise-shaping bandpass ADC. IEEE Trans Circuit Syst I, 2017, 99: 1[16] Sehgal R, Goes F V D, Bult K. A 13-mW 64-dB SNDR 280-MS/s pipelined ADC using linearized integrating amplifiers. IEEE J Solid-State Circuits, 2018, 53: 1878 doi: 10.1109/JSSC.2018.2815654 -
Proportional views






 DownLoad:
DownLoad: