| Citation: |
G. Trimarchi. Crystal structure prediction in the context of inverse materials design[J]. Journal of Semiconductors, 2018, 39(7): 071004. doi: 10.1088/1674-4926/39/7/071004
****
G Trimarchi, Crystal structure prediction in the context of inverse materials design[J]. J. Semicond., 2018, 39(7): 071004. doi: 10.1088/1674-4926/39/7/071004.
|
Crystal structure prediction in the context of inverse materials design
DOI: 10.1088/1674-4926/39/7/071004
More Information
-
Abstract
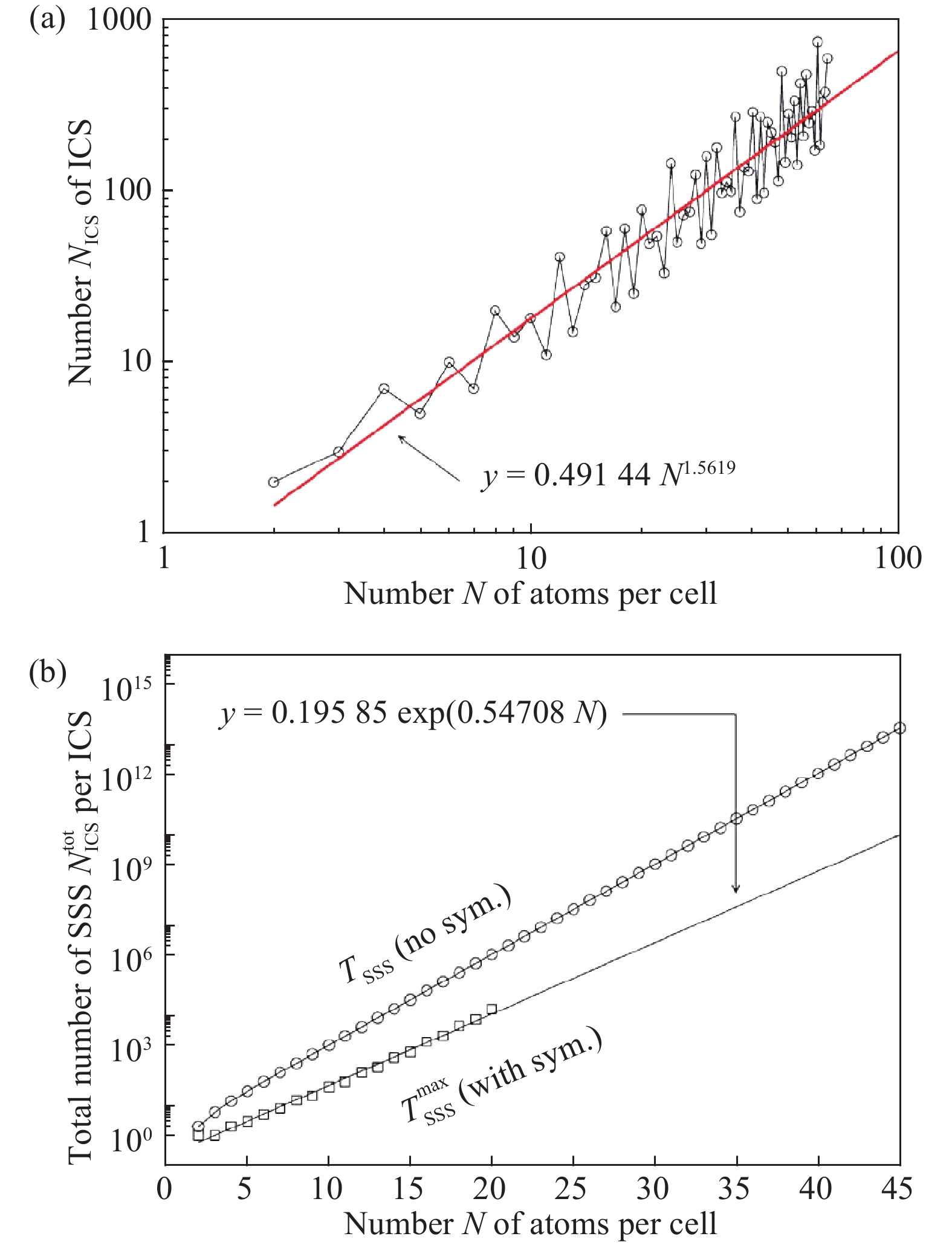
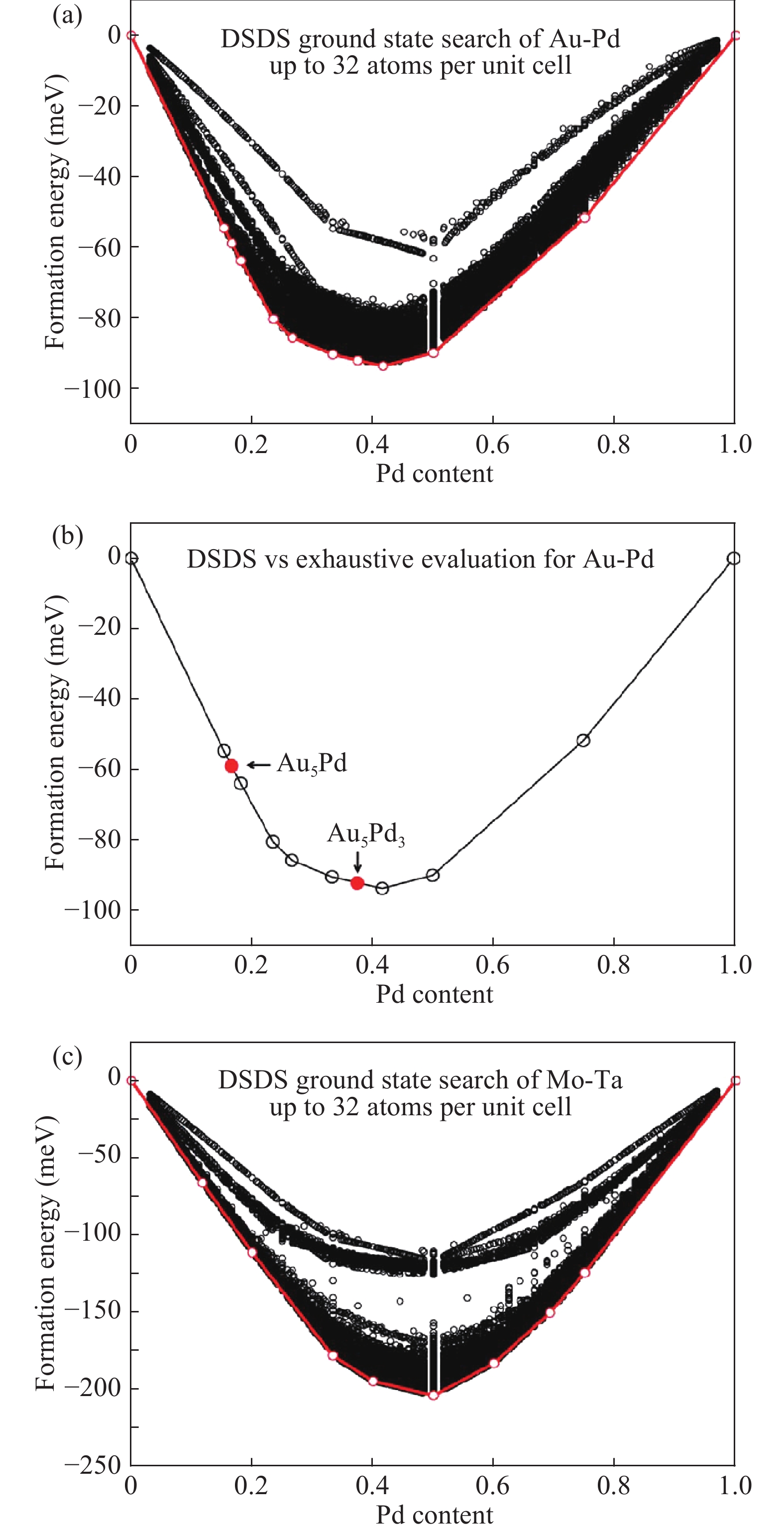
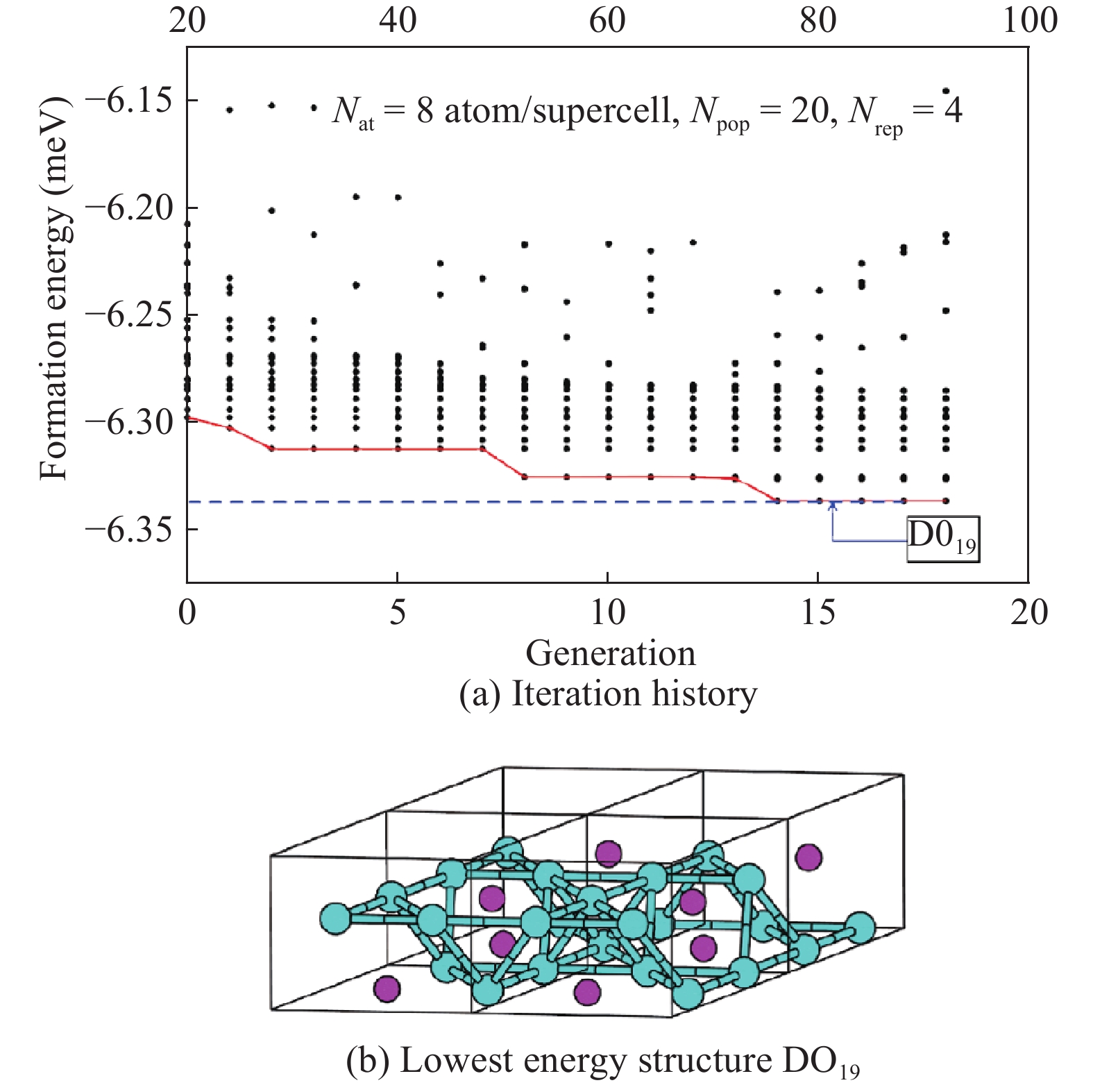
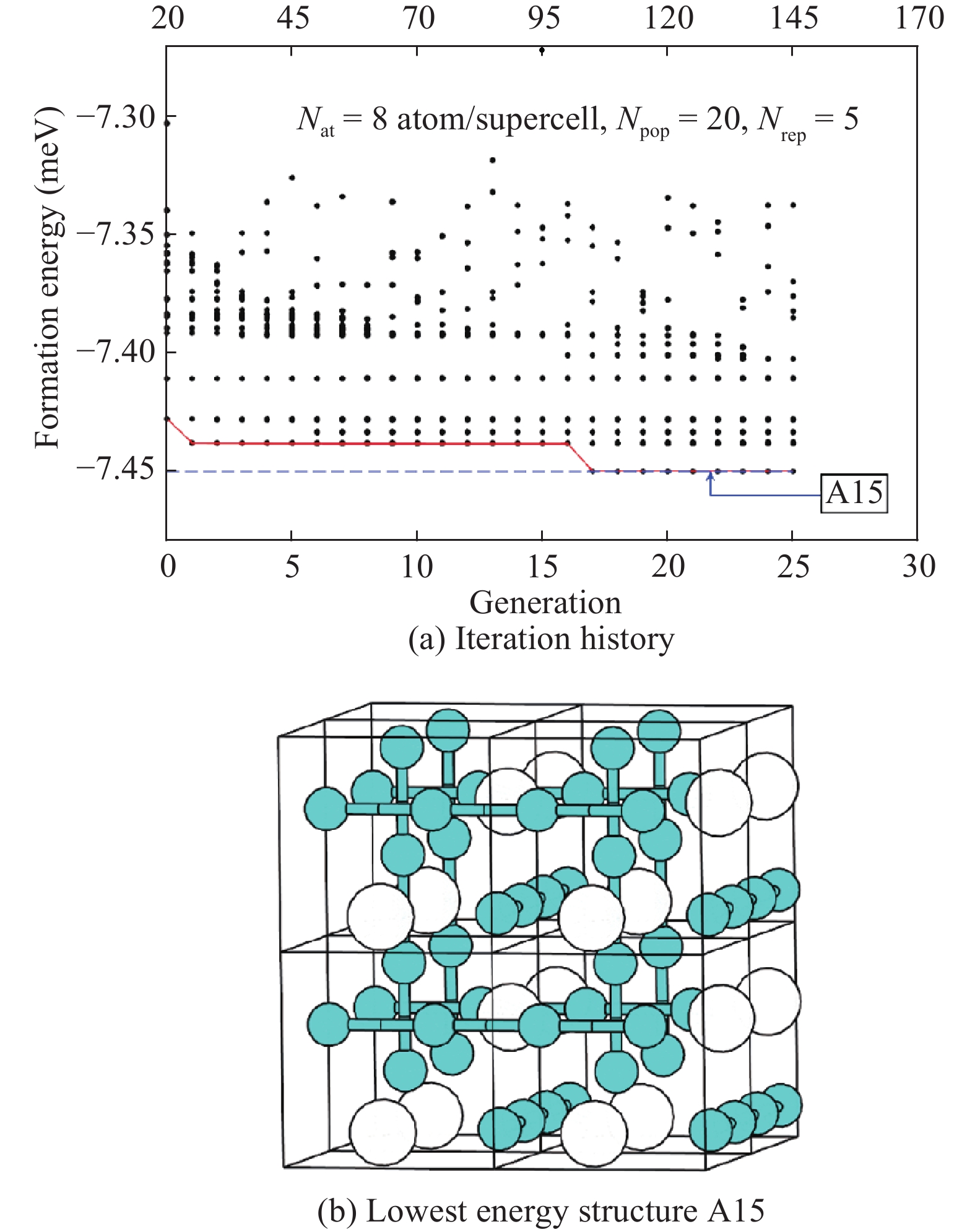
Inverse materials design tackles the challenge of finding materials with desired properties, tailored to specific applications, by combining atomistic simulations and optimization methods. The search for optimal materials requires one to survey large spaces of candidate solids. These spaces of materials can encompass both known and hypothetical compounds. When hypothetical compounds are explored, it becomes crucial to determine which ones are stable (and can be synthesized) and which are not. Crystal structure prediction is a necessary step for assessing theoretically the stability of a hypothetical material and, therefore, is a crucial step in inverse materials design protocols. Here, we describe how biologically-inspired global optimization methods can efficiently predict the stable crystal structure of solids. Specifically, we discuss the application of genetic algorithms to search for optimal atom configurations in systems in which the underlying lattice is given, and of evolutionary algorithms to address the general lattice-type prediction problem. -
References
[1] Martin R M. Electronic structure: basic theory and practical methods. Cambridge University Press, 2004[2] Martin R M, Reining L, Ceperley D M. Interacting electrons. Cambridge University Press, 2016[3] Franceschetti A, Zunger A. The inverse band-structure problem of finding an atomic configuration with given electronic properties. Nature, 1911, 402: 60[4] Inorganic Chemistry Structure Database (ICSD). Fachinformationszentrum, Karlsruhe, Karlsruhe, Germany, 2015[5] Trimarchi G, Zhang X, DeVries Vermeer M J, et al. Emergence of a few distinct structures from a single formal structure type during high-throughput screening for stable compounds: the case of RbCuS and RbCuSe. Phys Rev B, 2015, 92: 165103 doi: 10.1103/PhysRevB.92.165103[6] Zhang X, Yu L, Zakutayev A, et al. Sorting stable versus unstable hypothetical compounds: the case of multi-functional abx half-heusler filled tetrahedral structures. Adv Funct Mater, 2012, 22: 1425 doi: 10.1002/adfm.v22.7[7] Zhang X, Stevanović V, d’Avezac M, et al. Prediction of A2BX4 metal-chalcogenide compounds via first-principles thermodynamics. Phys Rev B, 2012, 86: 014109 doi: 10.1103/PhysRevB.86.014109[8] Woodley S M, Catlow R. Crystal structure prediction from first principles. Nat Mater, 2008, 7: 937 doi: 10.1038/nmat2321[9] Oganov A R. Modern methods of crystal structure prediction. 1st ed. Wiley-VCH, 2011[10] Goldberg D E. Genetic algorithms in search,optimization and machine learning. Addison-Wesley, Reading, MA, 1989[11] Eiben A E, Smith J E. Introduction to evolutionary computing. Berlin Heidelberg: Springer, 2003[12] Wells A F. Structural inorganic chemistry. 5th ed. Oxford University Press, 1984[13] Strukturbericht. Akademische Verlagsgesellschaft M. B. H, Leipzig, 1931, 1: 7[14] Trimarchi G, Graf P, Zunger A. Exploring the configurational space of binary alloys: Different sampling for different cell shapes. Phys Rev B, 2006, 74: 014204 doi: 10.1103/PhysRevB.74.014204[15] Ferreira L G, Wei S H, Zunger A. Stability, electronic structure, and phase diagrams of novel inter-semiconductor compounds. Int J Supercomput Appl, 1991, 5: 34 doi: 10.1177/109434209100500103[16] Barabash S V, Blum V, Müller S, et al. Prediction of unusual stable ordered structures of Au–Pd alloys via a first-principles cluster expansion. Phys Rev B, 2006, 74: 35108 doi: 10.1103/PhysRevB.74.035108[17] Zunger A. Statistics and dynamics of alloys phase transformations. New York: Plenum Press, 1994: 361[18] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing. Readings in Computer Vision, 1983, 220: 671 doi: 10.1142/9789812799371_0035[19] Kim K, Graf P A, Jones W B. A genetic algorithm based inverse band structure method for semiconductor alloys. J Comput Phys, 2005, 208: 735 doi: 10.1016/j.jcp.2005.03.005[20] Ihm J, Zunger A, Cohen M L. Momentum-space formalism for the total energy of solids. J Phys C, 1979, 12: 4409 doi: 10.1088/0022-3719/12/21/009[21] Doll K, Schön J C, Jansen M. Structure prediction based on ab initio simulated annealing for boron nitride. Phys Rev B, 2008, 78: 144110 doi: 10.1103/PhysRevB.78.144110[22] Martoňák R, Laio A, Parrinello M. predicting crystal structures: the parrinello-rahman method revisited. Phys Rev Lett, 2003, 90: 075503 doi: 10.1103/PhysRevLett.90.075503[23] Laio A, Parrinello M. Escaping free-energy minima. Proce Natl Acad Scie, 2002, 99: 12562 doi: 10.1073/pnas.202427399[24] Wales D J, Doye J P K. Global optimization by basin-hopping and the lowest energy structures of lennard-jones clusters containing up to 110 atoms. J Phys Chem A, 1997, 101: 5111 doi: 10.1021/jp970984n[25] Wales D J, Scheraga H A. Global optimization of clusters, crystals, and biomolecules. Science, 1999, 285: 1368 doi: 10.1126/science.285.5432.1368[26] Goedecker S. Minima hopping: an efficient search method for the global minimum of the potential energy surface of complex molecular systems. J Chem Phys, 2004, 120: 9911 doi: 10.1063/1.1724816[27] Amsler M, Goedecker S. Crystal structure prediction using the minima hopping method. J Chem Phys, 2010, 133: 224104 doi: 10.1063/1.3512900[28] Pickard C J, Needs R J. High-pressure phases of silane. Phys Rev Lett, 2006, 97: 045504 doi: 10.1103/PhysRevLett.97.045504[29] Pickard C J, Needs R J. Ab initio random structure searching. J Phys: Conden Matter, 2011, 23: 053201 doi: 10.1088/0953-8984/23/5/053201[30] Needs R J, Pickard C J. Perspective: role of structure prediction in materials discovery and design. APL Mater, 2016, 4: 053210 doi: 10.1063/1.4949361[31] Woodley S M, Battle P D, Gale J D, et al. The prediction of inorganic crystal structures using a genetic algorithm and energy minimisation. Phys Chem Chem Phys, 1999, 1: 2535 doi: 10.1039/a901227c[32] Zhao X, Nguyen M C, Zhang W Y, et al. Exploring the structural complexity of intermetallic compounds by an adaptive genetic algorithm. Phys Rev Lett, 2014, 112: 045502 doi: 10.1103/PhysRevLett.112.045502[33] Oganov A R, Glass C W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J Chem Phys, 2006, 124: 244704 doi: 10.1063/1.2210932[34] Oganov A R, Glass C W, Ono S. High-pressure phases of CaCO3: Crystal structure prediction and experiment. Earth Planet Sci Lett, 2006, 241: 95 doi: 10.1016/j.jpgl.2005.10.014[35] Abraham N L, Probert M I J. Improved real-space genetic algorithm for crystal structure and polymorph prediction. Phys Rev B, 2008, 77: 134117 doi: 10.1103/PhysRevB.77.134117[36] Abraham N L, Probert M I J. A periodic genetic algorithm with real-space representation for crystal structure and polymorph prediction. Phys Rev B, 2006, 73: 224104 doi: 10.1103/PhysRevB.73.224104[37] Lyakhov A O, Oganov A R, Stokes H T, et al. New developments in evolutionary structure prediction algorithm USPEX. Comput Phys Commun, 2013, 184: 1172 doi: 10.1016/j.cpc.2012.12.009[38] Lonie D C, Zurek E. XtalOpt: An open-source evolutionary algorithm for crystal structure prediction. Comput Phys Commun, 2011, 182: 372 doi: 10.1016/j.cpc.2010.07.048[39] Tipton W W, Hennig R G. A grand canonical genetic algorithm for the prediction of multi-component phase diagrams and testing of empirical potentials. J Phys: Conden Matter, 2013, 25: 495401 doi: 10.1088/0953-8984/25/49/495401[40] Wang Y, Lv J, Zhu L, Ma Y. CALYPSO: a method for crystal structure prediction. Comput Phys Commun, 2012, 183: 2063 doi: 10.1016/j.cpc.2012.05.008[41] Wang Y, Lv J, Zhu L, Ma Y. Crystal structure prediction via particle-swarm optimization. Phys Rev B, 2010, 82: 094116 doi: 10.1103/PhysRevB.82.094116[42] Trimarchi G, Zunger A. Global space-group optimization problem: Finding the stablest crystal structure without constraints. Phys Rev B, 2007, 75: 104113 doi: 10.1103/PhysRevB.75.104113[43] Trimarchi G, Zunger A. Finding the lowest-energy crystal structure starting from randomly selected lattice vectors and atomic positions: first-principles evolutionary study of the Au–Pd, Cd–Pt, Al–Sc, Cu–Pd, Pd–Ti, and Ir–N binary systems. J Phys: Conden Matter, 2008, 20: 295212 doi: 10.1088/0953-8984/20/29/295212[44] Glass C W, Oganov A R, Hansen N. USPEX—evolutionary crystal structure prediction. Comput Phys Commun, 2006, 175: 713 doi: 10.1016/j.cpc.2006.07.020[45] Deaven D M, Ho K M. Molecular geometry optimization with a genetic algorithm. Phys Rev Lett, 1995, 75: 288 doi: 10.1103/PhysRevLett.75.288[46] Trimarchi G, Freeman A J, Zunger A. Predicting stable stoichiometries of compounds via evolutionary global space-group optimization. Phys Rev B, 2009, 80: 092101 doi: 10.1103/PhysRevB.80.092101[47] Blum V, Zunger A. Structural complexity in binary bcc ground states: The case of bcc Mo-Ta. Phys Rev B, 2004, 69: 020103 doi: 10.1103/PhysRevB.69.020103[48] Blum V, Zunger A. Mixed-basis cluster expansion for thermodynamics of bcc alloys. Phys Rev B, 2004, 70: 155108 doi: 10.1103/PhysRevB.70.155108[49] Blum V, Zunger A. Prediction of ordered structures in the bcc binary systems of Mo, Nb, Ta, and W from first-principles search of approximately 3 000 000 possible configurations. Phys Rev B, 2005, 72: 020104 doi: 10.1103/PhysRevB.72.020104[50] Sanati M, Wang L G, Zunger A. Adaptive crystal structures: CuAu and NiPt. Phys Rev Lett, 2003, 90: 045502 doi: 10.1103/PhysRevLett.90.045502[51] Gautier R, Zhang X, Hu L, et al. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat Chem, 2015, 7: 308 doi: 10.1038/nchem.2207[52] Massalski T B. Binary alloy phase diagrams. ASM International, 1992[53] Villars P, Cenzual K, Daams J L C, et al. Inorganic materials database and design system. ASM International, 2003[54] Fujikawa S, Sugaya M, Takei H, et al. Solid solubility and residual resistivity of scandium in aluminum. J Less-Common Met, 1979, 63: 87 doi: 10.1016/0022-5088(79)90211-X[55] Curtarolo S, Morgan D, Ceder G. Accuracy of ab initio methods in predicting the crystal structures of metals: a review of 80 binary alloys. Calphad, 2005, 29: 163 doi: 10.1016/j.calphad.2005.01.002[56] Raub E, Röschel E. Die Titan-Palladium-Legierungen. Z Metallkd, 1968, 59: 112 -
Proportional views






 DownLoad:
DownLoad: