| Citation: |
Qiankun Wang, Changchun Chai, Yuqian Liu, Yintang Yang. The influence of pulsed parameters on the damage of a Darlington transistor[J]. Journal of Semiconductors, 2018, 39(9): 094005. doi: 10.1088/1674-4926/39/9/094005
****
Q K Wang, C C Chai, Y Q Liu, Y T Yang, The influence of pulsed parameters on the damage of a Darlington transistor[J]. J. Semicond., 2018, 39(9): 094005. doi: 10.1088/1674-4926/39/9/094005.
|
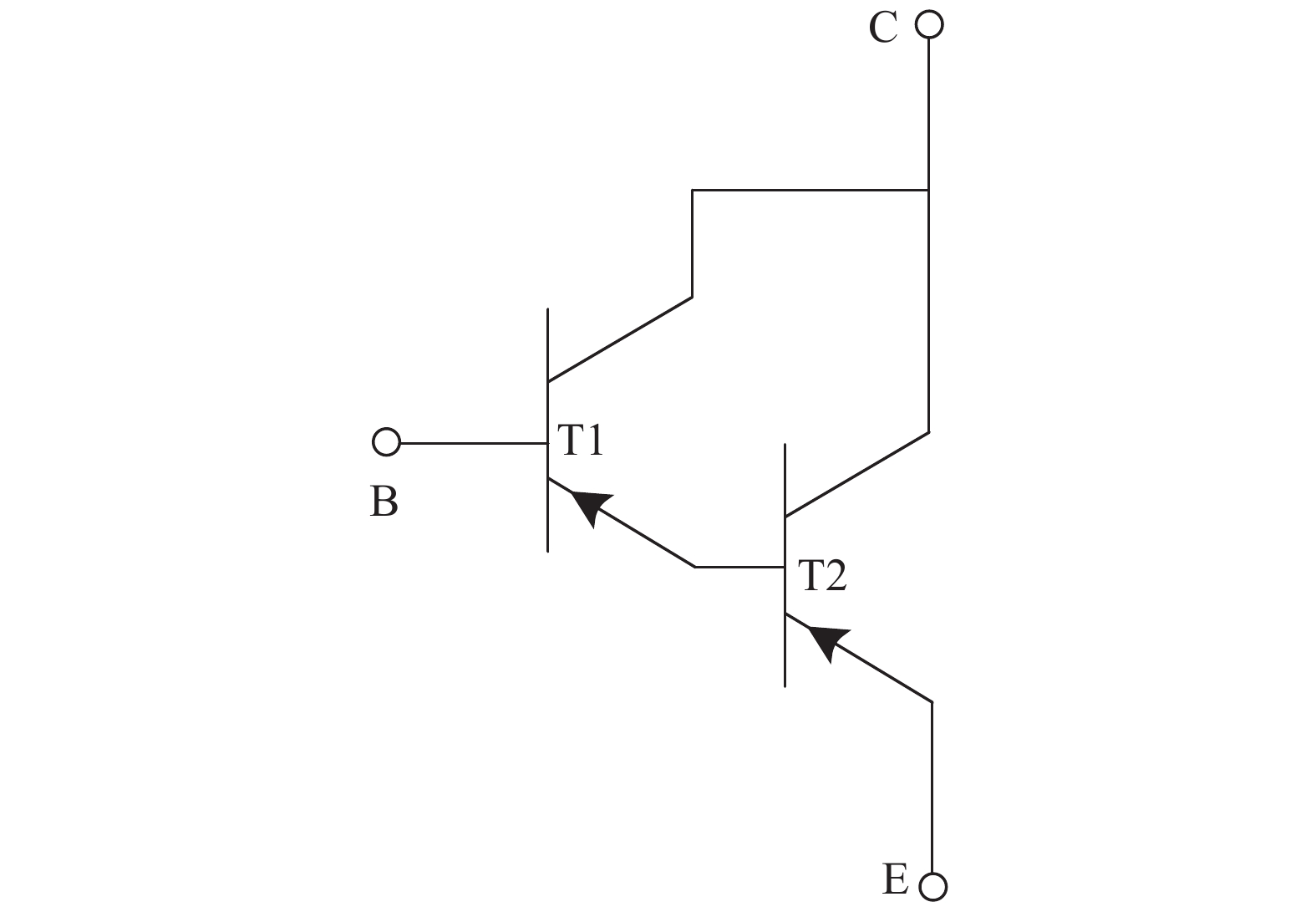
The influence of pulsed parameters on the damage of a Darlington transistor
DOI: 10.1088/1674-4926/39/9/094005
More Information
-
Abstract
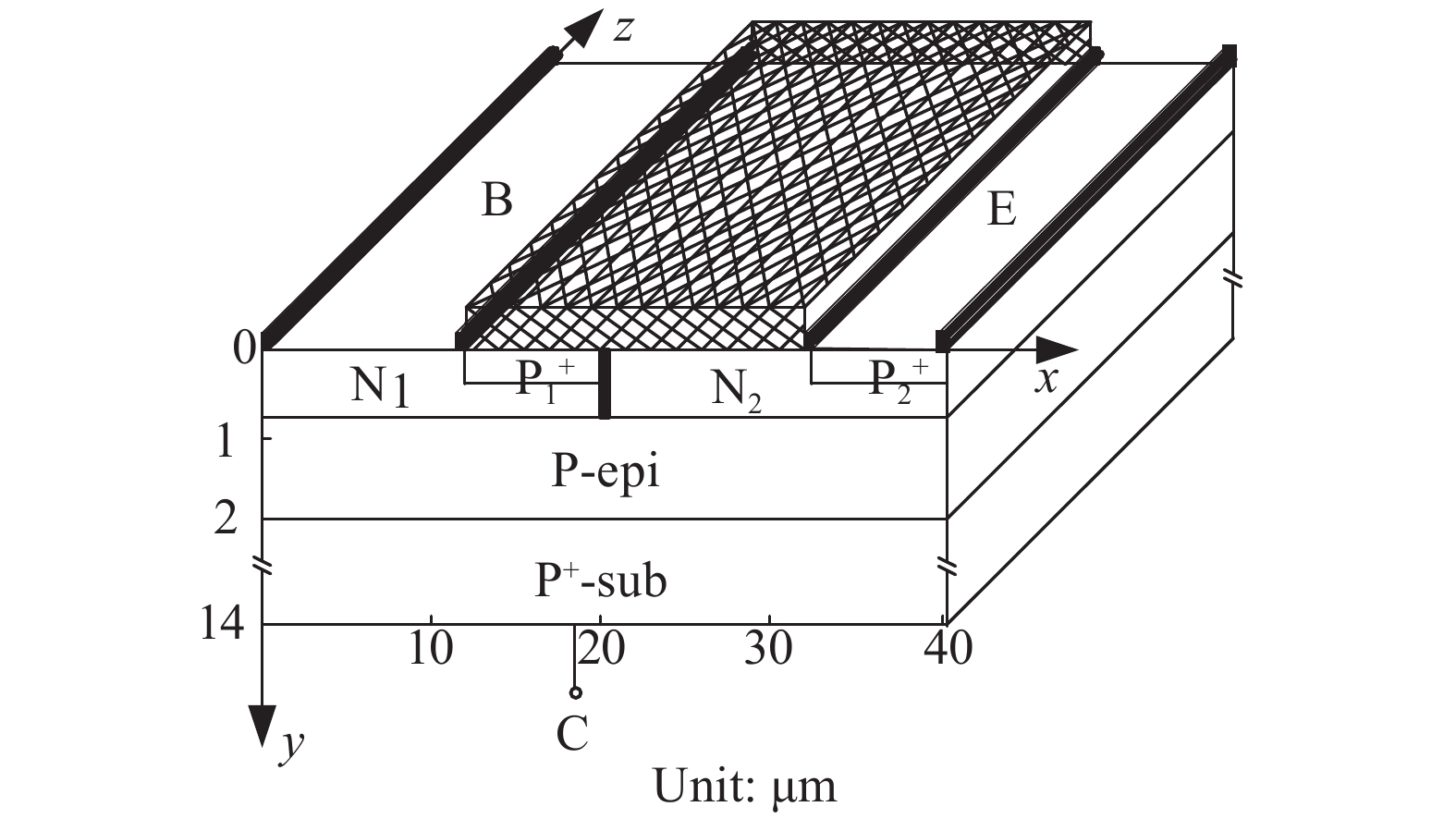
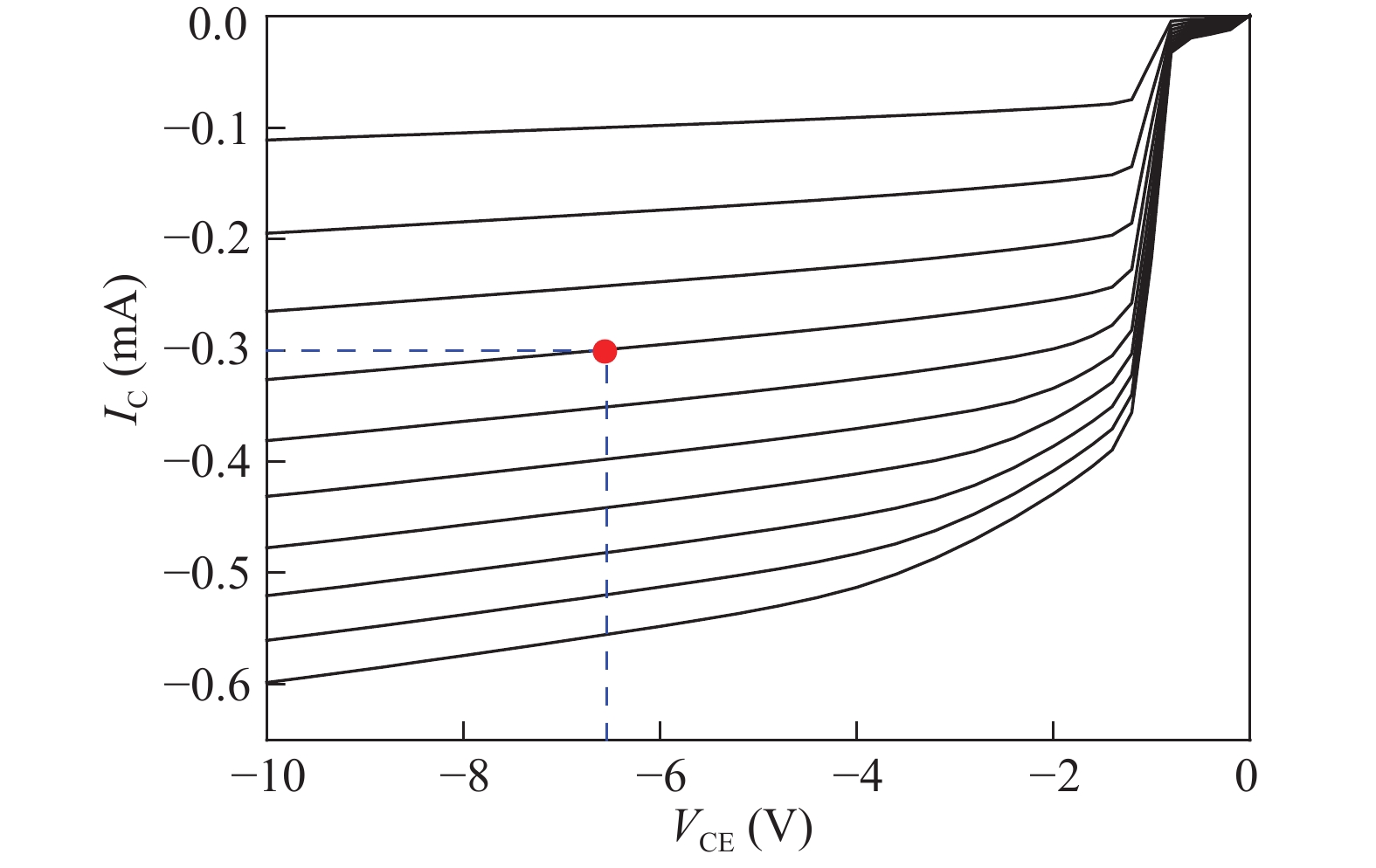
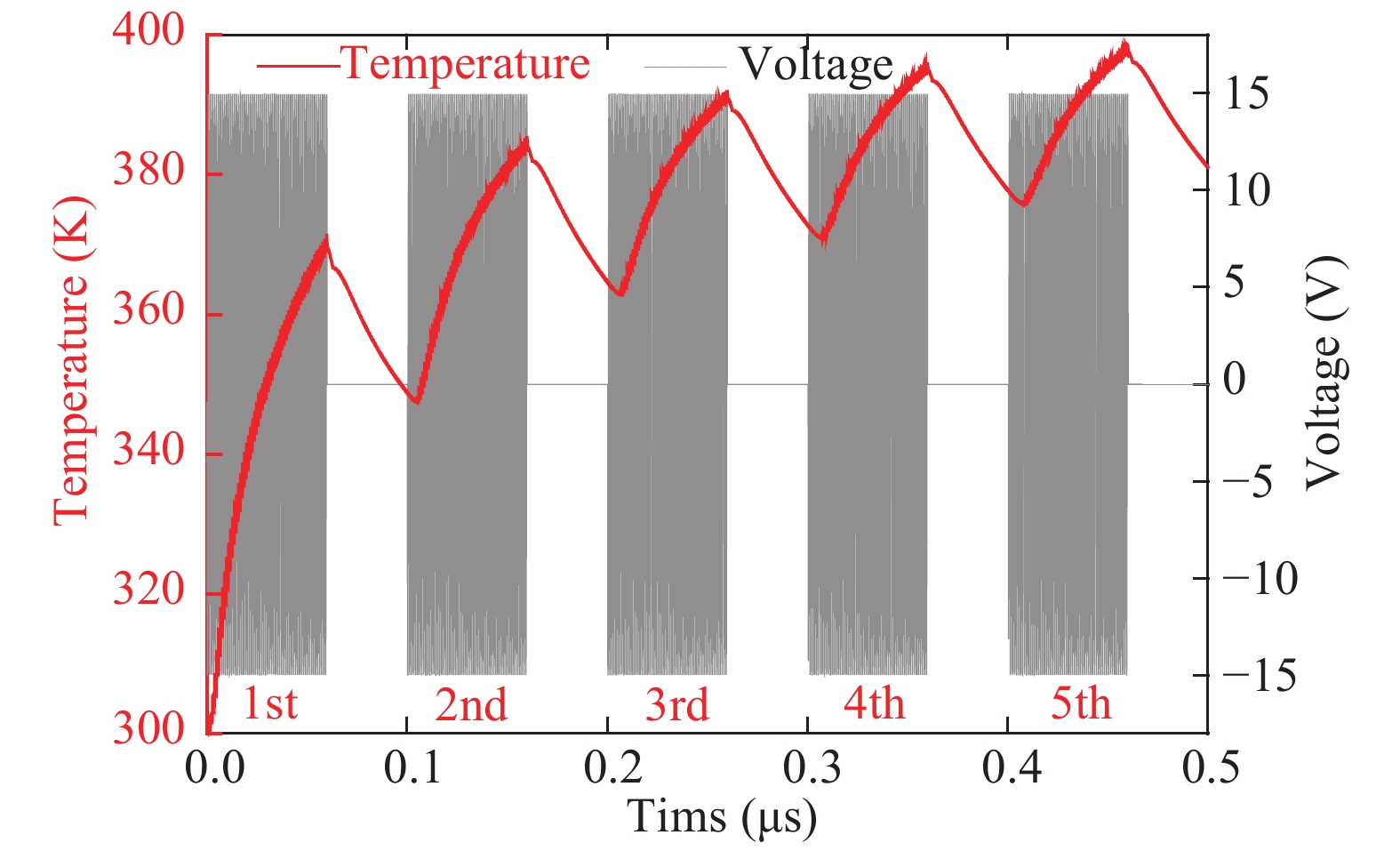
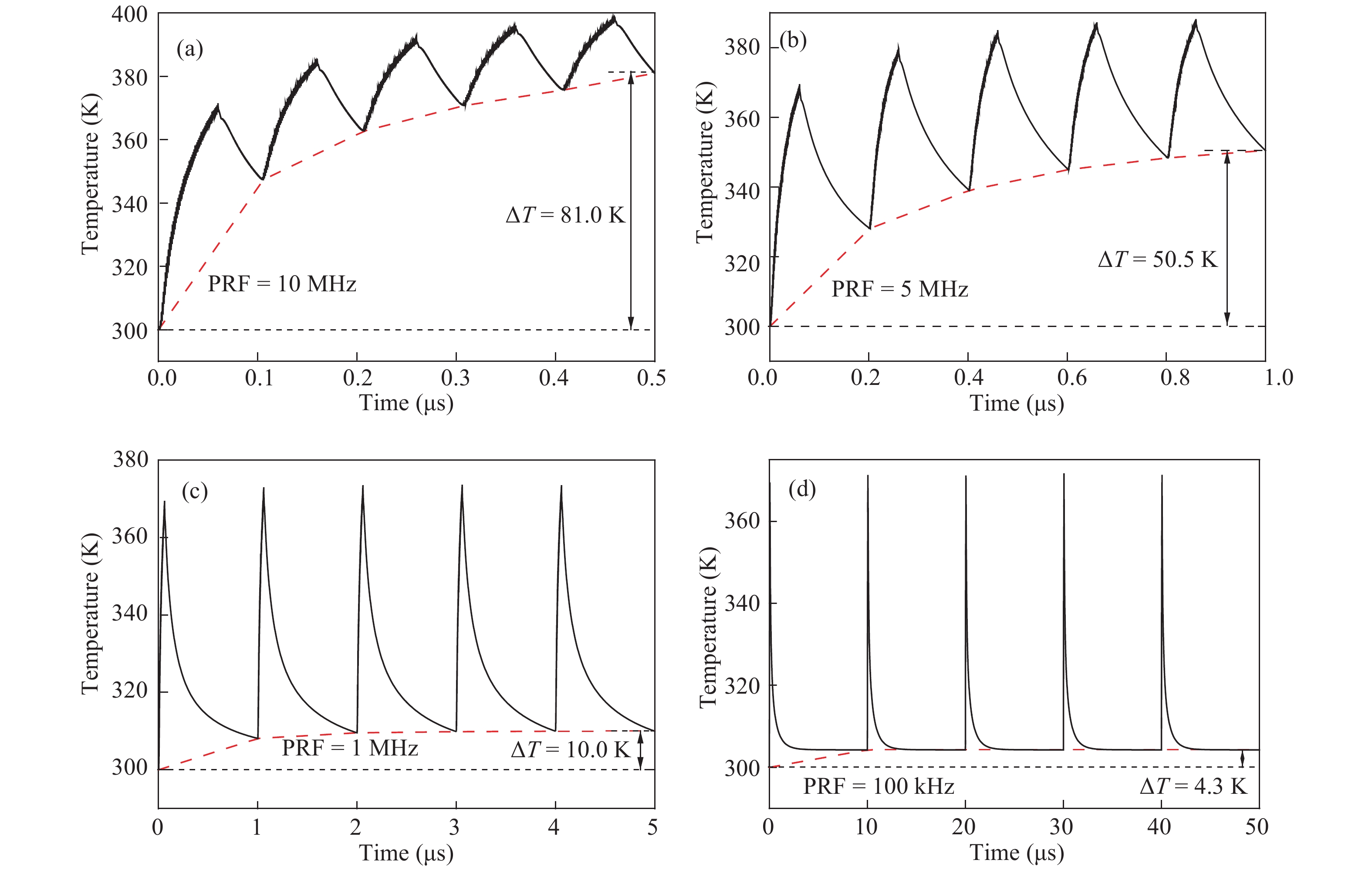
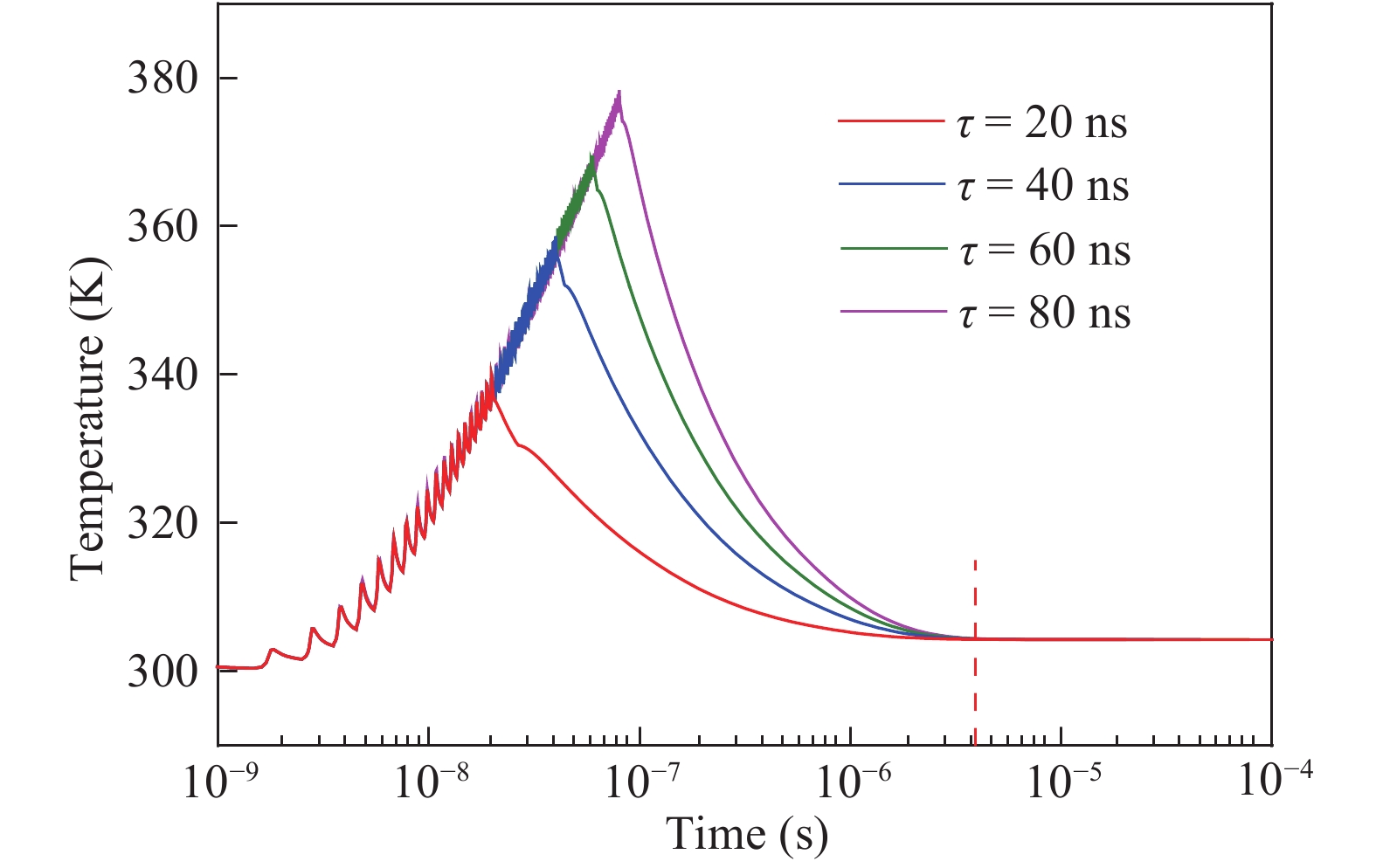
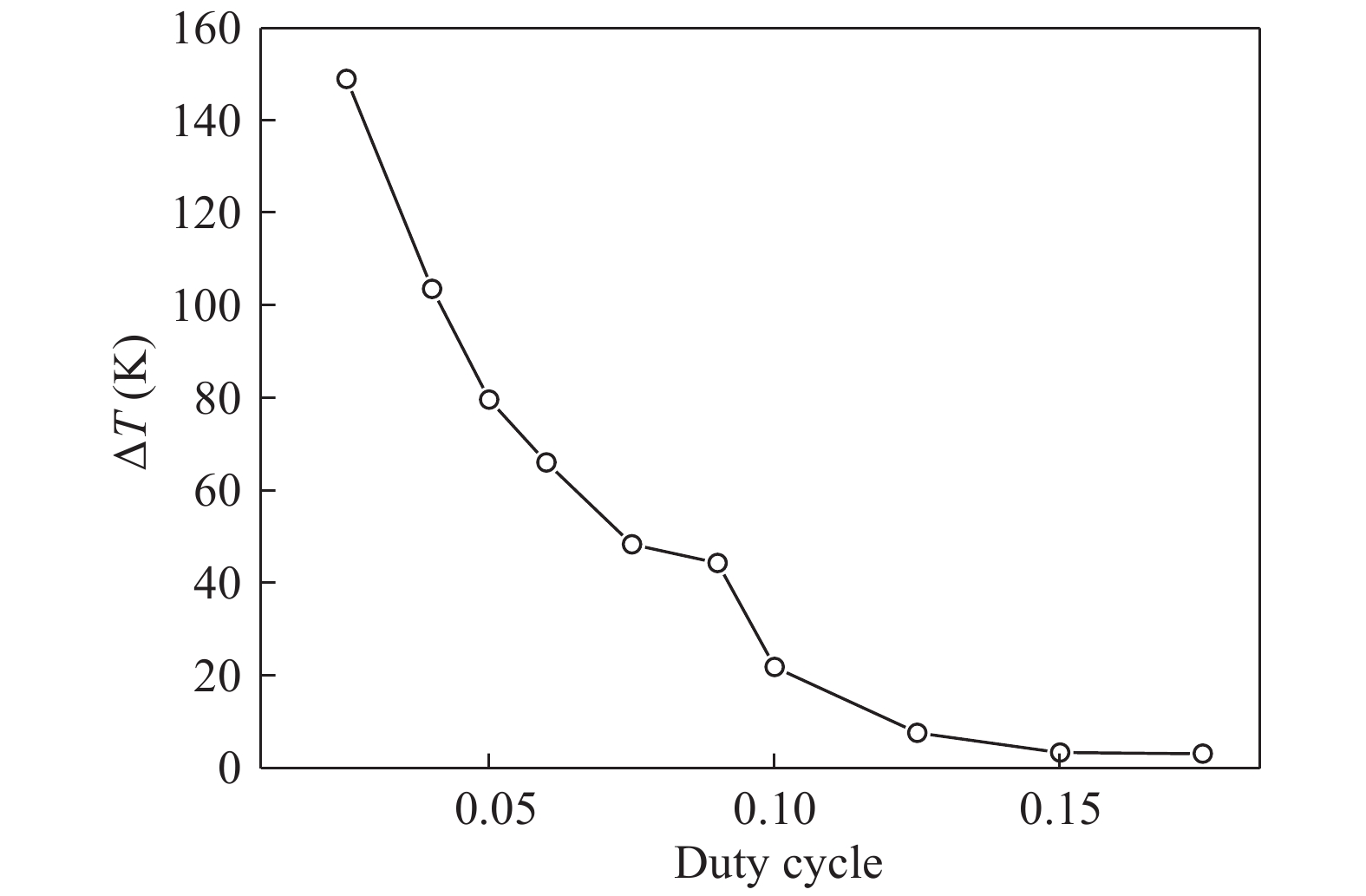
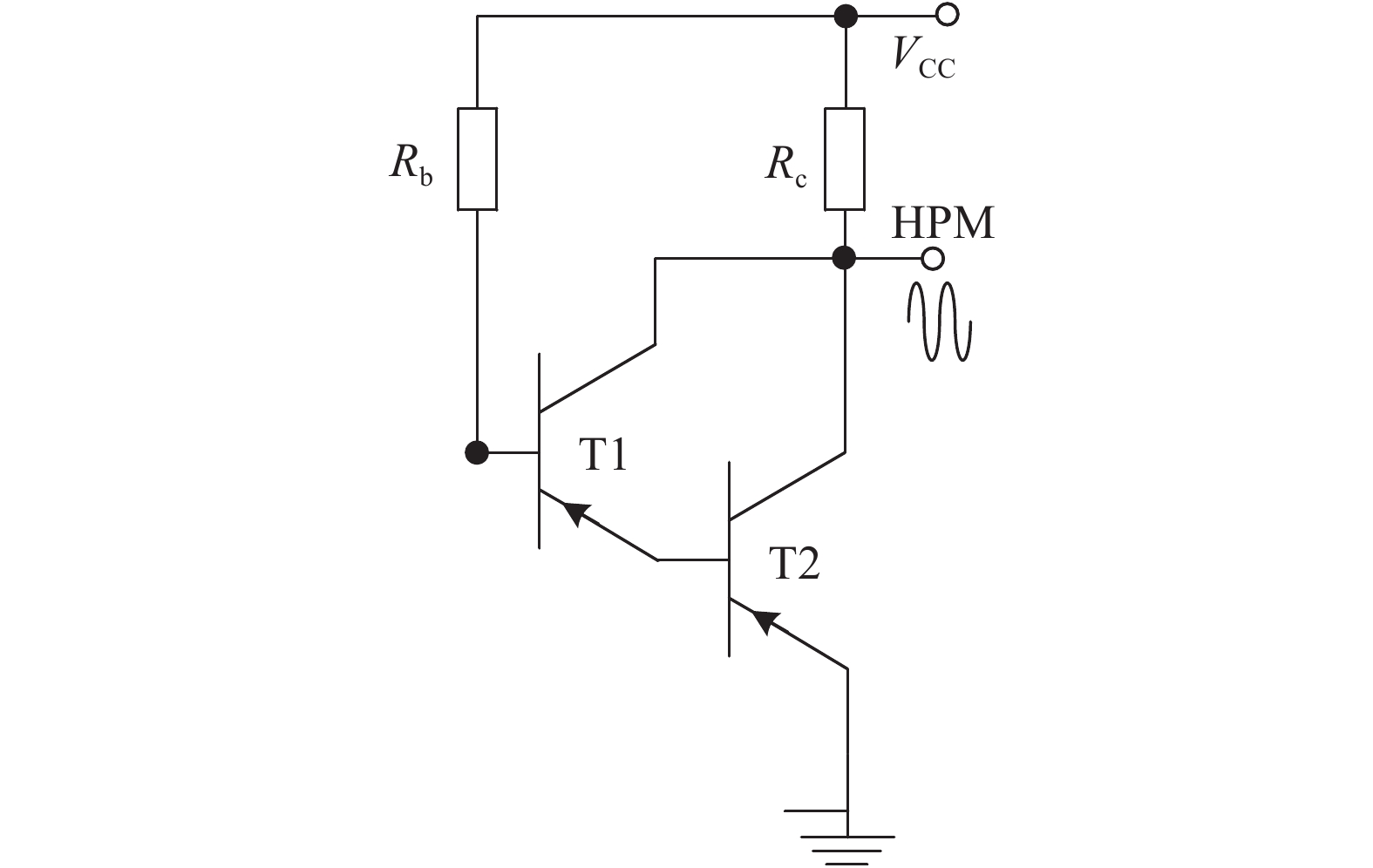
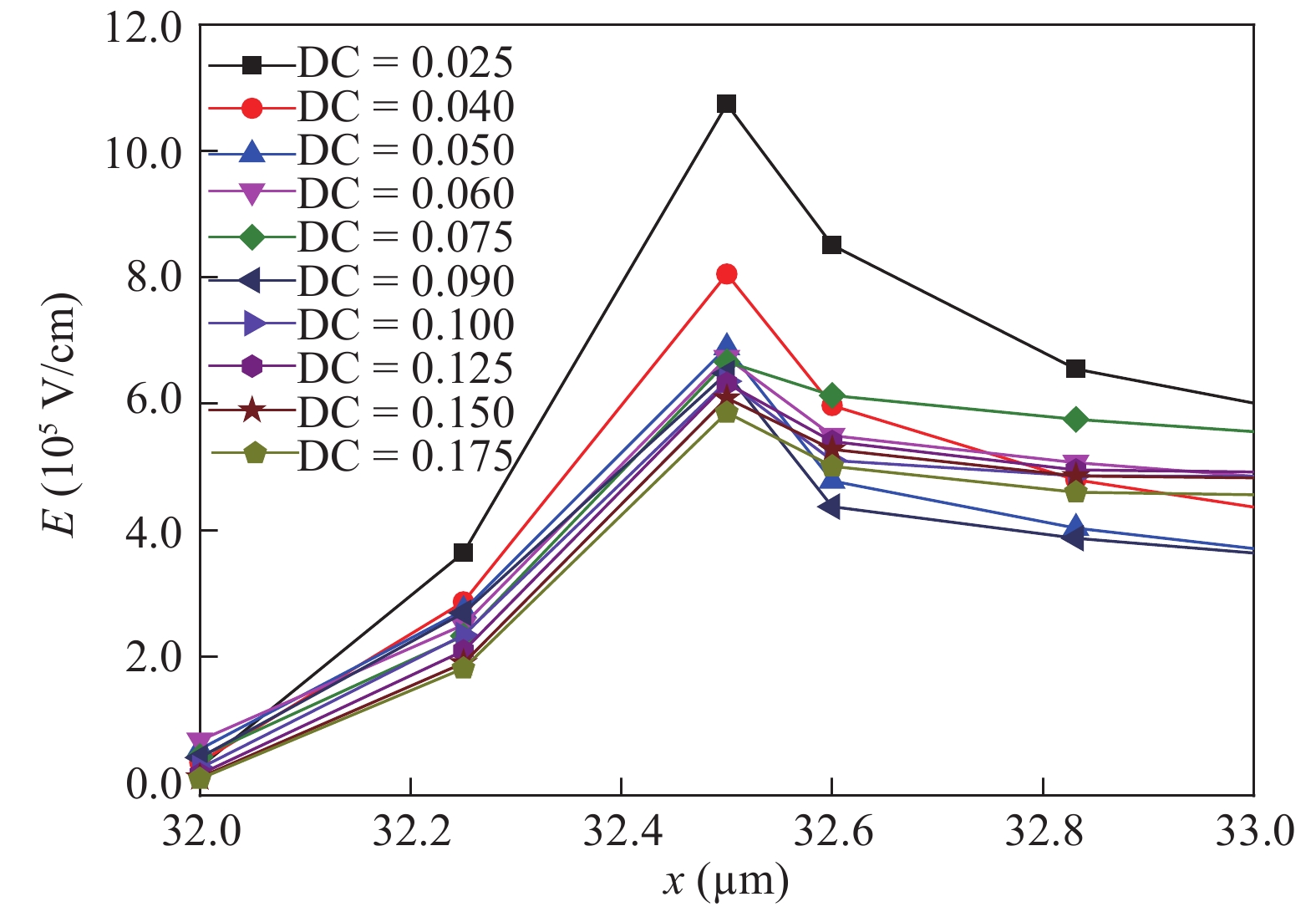
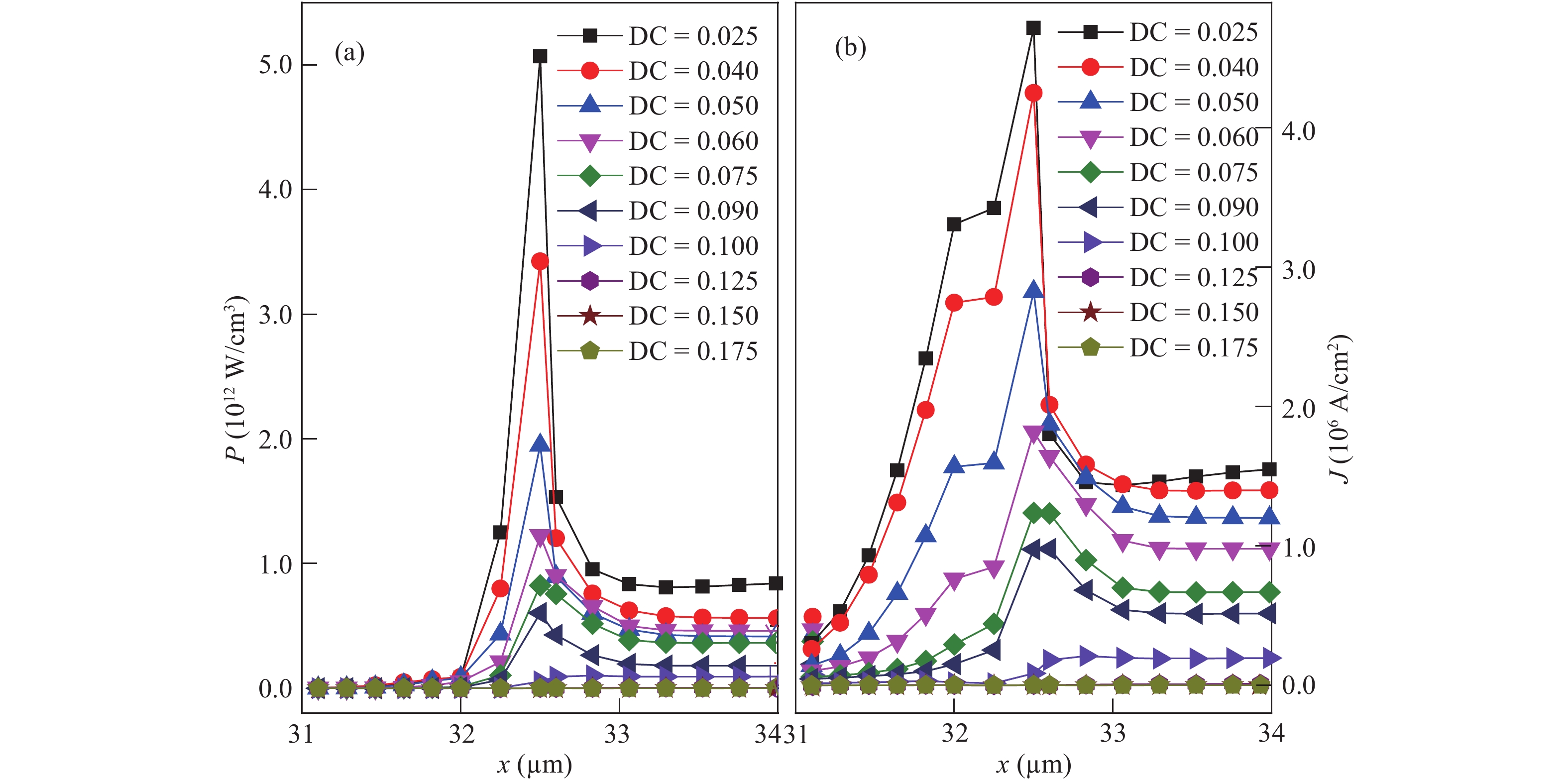
Theoretical research on the heat accumulation effect of a Darlington transistor induced by high power microwave is conducted, and temperature variation as functions of pulse repetitive frequency (PRF) and duty cycle (DC) are studied. According to the distribution of the electronic field and the current density in the Darlington transistor, the research of the damage mechanism is carried out. The results show that for repetitive pulses with the same pulse widths and different PRFs, the value of temperature variation increases with PRF increases, and the peak temperature has almost no change when PRF is lower than 200 kHz; while for the repetitive pulses with the same PRF and different pulse widths, the larger the pulse width is, the greater temperature variation varies. The response of the peak temperature caused by a single pulse demonstrates that there is no temperature variation when the rising time is much shorter than the falling time. In addition, the relationship between the temperature variation and the time during the rising edge time as well as that between the temperature variation and the time during the falling edge time are obtained utilizing the curve fitting method. Finally, for a certain average power, with DC increases the value of temperature variation decreases. -
References
[1] Krzikalla R, Luiken J, Ter Haneborg L, et al. Systematic description of the protection capability of protection elements. IEEE International Symposium on Electromag Compat, 2007, 179: 1[2] Bayram Y, Chang P C, Volakis J L, et al. High power EMI on digital circuits within automotive structures. IEEE Int Symp Electromagn Compat, 2006, 2: 507[3] Hwang S M, Hong J I, Huh C S. Characterization of susceptibility of integrated circuits with induction caused by high power microwaves. Prog Electromagn Res, 2008, 81: 61 doi: 10.2528/PIER07121704[4] Mansson D, Thottappillil R, Nilsson T, et al. Susceptibility of civilian GPS receivers to electromagnetic radiation. IEEE Trans Electromagn Compat, 2008, 50(2): 434 doi: 10.1109/TEMC.2008.921015[5] Sabath F, Backstrom M, Nordstrom B, et al. Overview of four European high-power microwave narrow-band test facilities. IEEE Trans Electromagn Compat, 2004, 46(3): 329 doi: 10.1109/TEMC.2004.831822[6] Fan J P, Zhang L, Jia X Z. HPM damage mechanism on bipolar transistors. High Power Laser Part. Beams, 2010, 22: 1319 doi: 10.3788/HPLPB[7] Radasky W A, Baum C E, Wik M W. Introduction to the special issue on high-power electromagnetics (HPEM) and intentional electromagnetics interference (IEMI). IEEE Trans Electromagn Compat, 2004, 46(3): 314 doi: 10.1109/TEMC.2004.831899[8] Ma Z Y, Chai C C, Ren X R, et al. Effects of microwave pulse-damage on a bipolar transistor. Chin Phys B, 2012, 21: 058502 doi: 10.1088/1674-1056/21/5/058502[9] Ma Z Y, Chai C C, Ren X R, et al. Microwave damage susceptibility trend of a bipolar transistor as a function of frequency. Chin Phys B, 2012, 21: 098502 doi: 10.1088/1674-1056/21/9/098502[10] Klunder C, Haneborg J L. Effects of high-power and transient disturbances on wireless communication systems operating inside the 2.4 GHz ISM band. IEEE Int Symp Electromagn Compat Fort Lauderdale, FL, USA, 2010, 359[11] Nitsch D, Camp M, Sabath F, et al. Susceptibility of some electronic equipment to HPEM threats. IEEE Trans Electromagn Compat, 2004, 46(3): 380 doi: 10.1109/TEMC.2004.831842[12] BackStrom M G, Lovstrand K G. Susceptibility of electronic system by high power microwave: summary of test experience. IEEE Trans Electromagn Compat, 2004, 46(3): 396 doi: 10.1109/TEMC.2004.831814[13] Ma Z Y, Chai C C, Ren X R, et al. The pulsed microwave damage trend of a bipolar transistor as a function of pulse parameters. Chin Phys B, 2013, 22: 028502 doi: 10.1088/1674-1056/22/2/028502[14] Integrated Systems Engineering Corp. ISE-TCAD Dessis Simulation Users Manual, Zurich, Switzerland, 2004, 142[15] Radasky W A. Protection of commercial installations from the high-frequency electromagnetic threats of HEPM and IEMI using IEC standards. Asia-Pacific Symposium on Electromagnetic Compatibility, Beijing, China, 2010: 758[16] Anghel C, Gillon R, Ionescu A M. Self-heating characterization and extraction method for thermal resistance and capacitance. IEEE Electron Device Lett, 2004, 25(3): 141 doi: 10.1109/LED.2003.821669 -
Proportional views





 DownLoad:
DownLoad: