Fig. 1.
Relational curves of the vibrational frequency (VF) λ with the barrier height of the quantum well (QW) V0 and the range of the asymmetrical Gaussian confinement potential R.
DownLoad:
| Citation: |
Wei Xiao, Jinglin Xiao. The energy-level and vibrational frequency properties of a polaron weak-coupled in a quantum well with asymmetrical Gaussian confinement potential[J]. Journal of Semiconductors, 2019, 40(4): 042901. doi: 10.1088/1674-4926/40/4/042901
****
W Xiao, J L Xiao, The energy-level and vibrational frequency properties of a polaron weak-coupled in a quantum well with asymmetrical Gaussian confinement potential[J]. J. Semicond., 2019, 40(4): 042901. doi: 10.1088/1674-4926/40/4/042901.
|
The energy-level and vibrational frequency properties of a polaron weak-coupled in a quantum well with asymmetrical Gaussian confinement potential
DOI: 10.1088/1674-4926/40/4/042901
More Information
-
Abstract
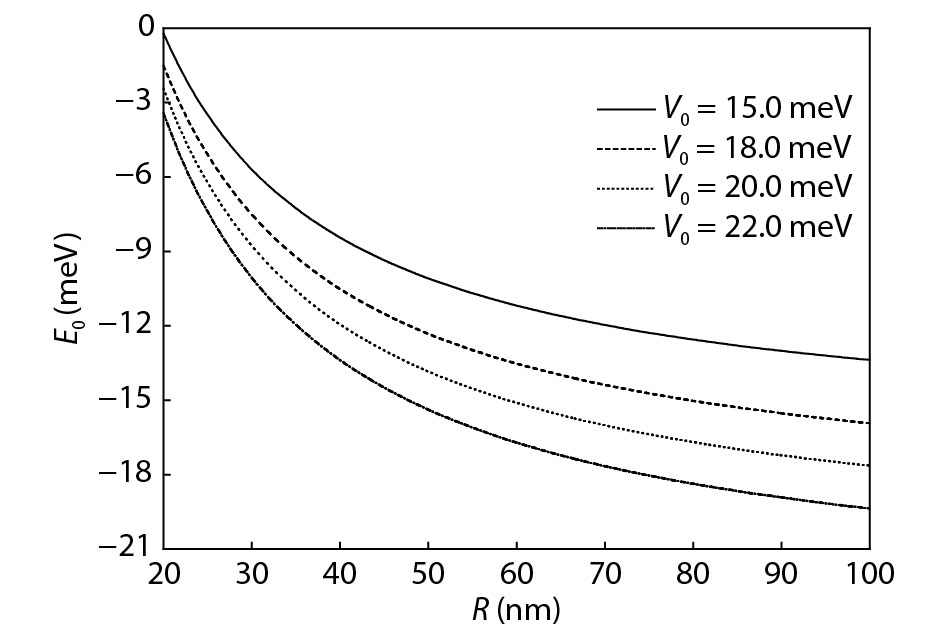
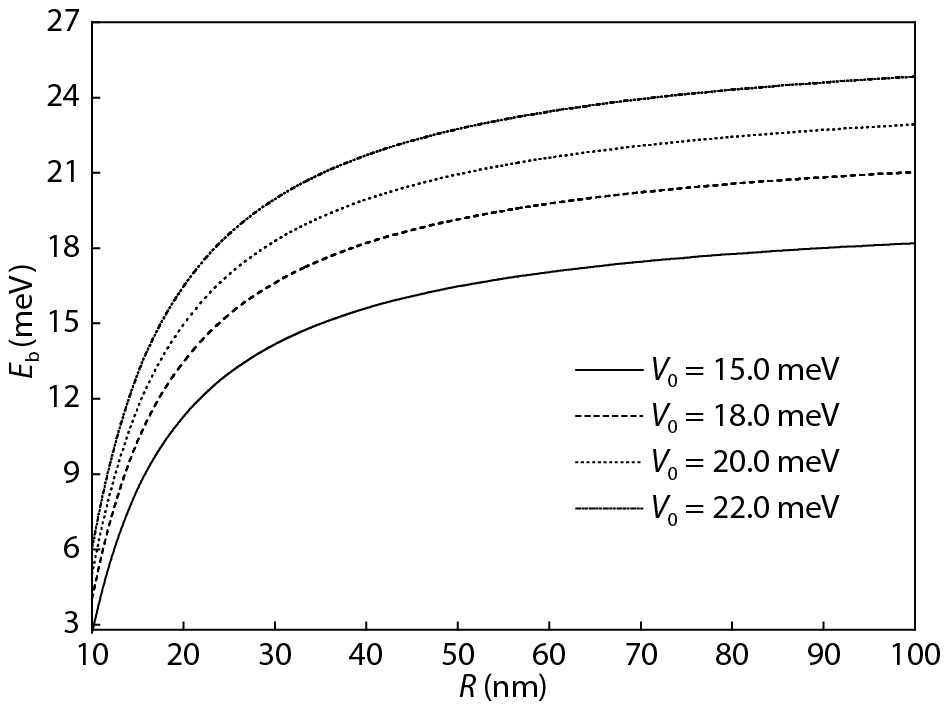
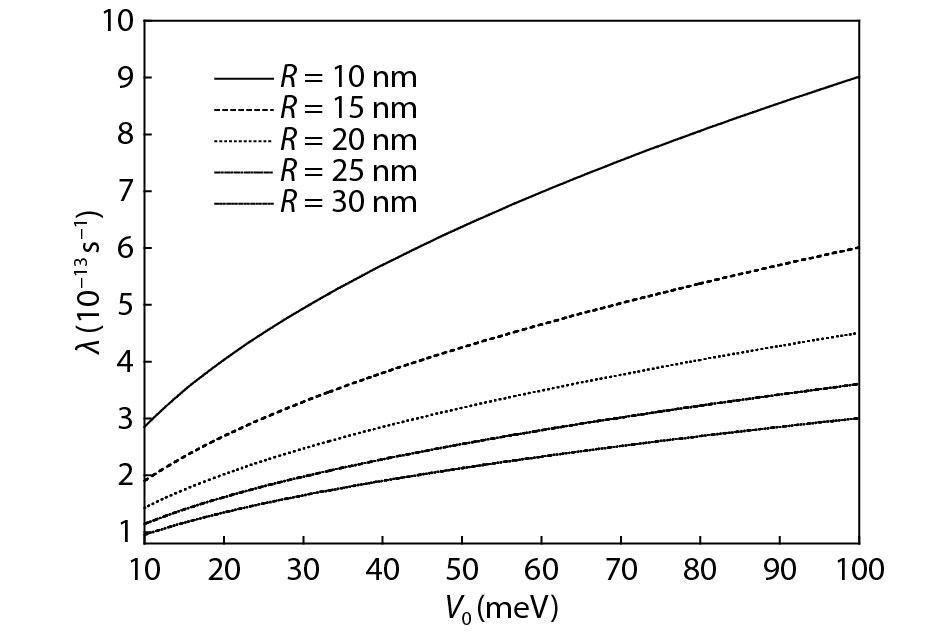
The vibrational frequency (VF), the ground state (GS) energy and the GS binding energy of the weak electron-phonon coupling polaron in a quantum well (QW) with asymmetrical Gaussian confinement potential are calculated. First we introduce the linear combination operator to express the momentum and coordinates in the Hamilton and then operate the system Hamilton using unitary transformation. The results indicate the relations of the quantities (the VF, the absolute value of GS energy and the GS binding energy) and the parameters (the QW barrier height and the range of Gaussian confinement potential in the growth direction of the QW). -
References
[1] Ozturk O, Ozturk E, Elagoz S. The effect of barrier width on the electronic properties of double GaAlAs/GaAs and GaInAs/GaAs quantum wells. J Mol Struct, 2018, 1156, 726 doi: 10.1016/j.molstruc.2017.12.012[2] Samokhvalov P S, Linkov P A, Zvaigzne M A, et al. Optical properties of core-multishell quantum dots. KnE Energy Phys, 2018, 3(2), 449 doi: 10.18502/ken.v3i2.1850[3] Cai Z, Liu B, Zou X, et al. Chemical vapor deposition growth and applications of two-dimensional materials and their heterostructures. Chem Rev, 2018, 118(13), 6091 doi: 10.1021/acs.chemrev.7b00536[4] Belitsch M, Gruber C, Ditlbacher H, et al. Gray state dynamics in the blinking of single type I colloidal quantum dots. Nano, 2018, 13(04), 1850039 doi: 10.1142/S179329201850039X[5] Müßener J, Ludwig A T, Kalinowski S, et al. Optical emission of GaN/AlN quantum-wires–the role of charge transfer from a nanowire template. Nanoscale, 2018, 10(12), 5591 doi: 10.1039/C7NR08057C[6] Chen L J. Synthesis and optical properties of lead-free cesium germanium halide perovskite quantum rods. RSC Adv, 2018, 8(33), 18396 doi: 10.1039/C8RA01150H[7] Moon P, Forsythe C, Zhou X, et al. Electronic structure engineering of graphene using patterned dielectric superlattices. Bull Am Phys Soc, 2018[8] Wu X, Li J, Briggeman M, et al. Breaking electron pairs in pseudogap state in SmTiO3/SrTiO3/SmTiO3 quantum wells. Bull Am Phys Soc, 2018[9] Ambacher O, Majewski J, Miskys C, et al. Pyroelectric properties of Al (In) GaN/GaN hetero-and quantum well structures. J Phys: Conden Matter, 2002, 14(13), 3399 doi: 10.1088/0953-8984/14/13/302[10] Makino T, Segawa Y, Kawasaki M, et al. Optical properties of excitons in ZnO-based quantum well heterostructures. Semicond Sci Technol, 2005, 20(4), S78 doi: 10.1088/0268-1242/20/4/010[11] Aumer M E, Leboeuf S F, Bedair S M, et al. Effects of tensile and compressive strain on the luminescence properties of AlInGaN/InGaN quantum well structures. Appl Phys Lett, 2000, 77(6), 821 doi: 10.1063/1.1306648[12] Nandi S. The quantum Gaussian well. Am J Phys, 2010, 78(12), 1341 doi: 10.1119/1.3474665[13] Wu J, Guo K, Liu G. Polaron effects on nonlinear optical rectification in asymmetrical Gaussian potential quantum wells with applied electric fields. Physica B, 2014, 446(9), 59 doi: 10.1016/j.physb.2014.04.013[14] Xiao J L. The effects of hydrogen-like impurity and temperature on state energies and transition frequency of strong-coupling bound polaron in an asymmetric gaussian potential quantum well. J Low Temp Phys, 2018, 192(1/2), 41 doi: 10.1007/s10909-018-1873-8[15] Xiao J L. Properties of strong-coupling polaron in an asymmetrical gaussian confinement potential quantum well. Journal of Inner Mongolia University for Nationalities, 2015, 30, 369[16] Lee T D, Low F E, Pines D. The motion of slow electrons in a polar crystal. Phys Rev, 1953, 90(2), 297 doi: 10.1103/PhysRev.90.297[17] Huybrechts W J. Note on the ground-state energy of the Feynman polaron model. J Physs C, 1976, 9(8), L211 doi: 10.1088/0022-3719/9/8/006[18] Devreese J T. Polarons in ionic crystals and polar semiconductors. Elsevier Science Publishing Co Inc., 1972 -
Proportional views
