| Citation: |
Guoping Luo, Yingmei Bian, Ruifeng Wu, Guoxia Lai, Xiangfu Xu, Weiwei Zhang, Xingyuan Chen. First principles study of the electronic structure and photovoltaic properties of β-CuGaO2 with MBJ + U approach[J]. Journal of Semiconductors, 2020, 41(10): 102102. doi: 10.1088/1674-4926/41/10/102102
****
G P Luo, Y M Bian, R F Wu, G X Lai, X F Xu, W W Zhang, X Y Chen, First principles study of the electronic structure and photovoltaic properties of β-CuGaO2 with MBJ + U approach[J]. J. Semicond., 2020, 41(10): 102102. doi: 10.1088/1674-4926/41/10/102102.
|
First principles study of the electronic structure and photovoltaic properties of β-CuGaO2 with MBJ + U approach
DOI: 10.1088/1674-4926/41/10/102102
More Information
-
Abstract
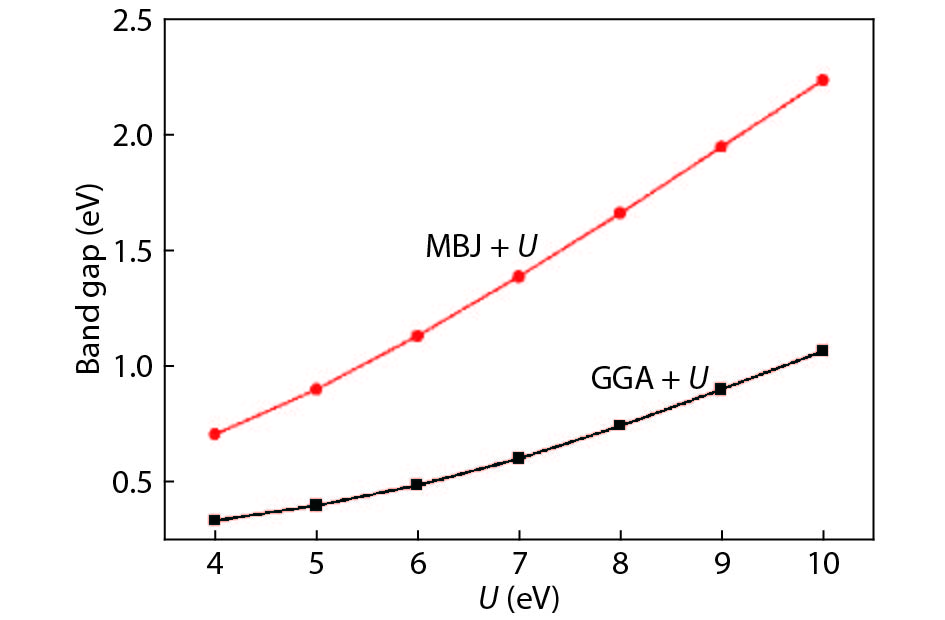
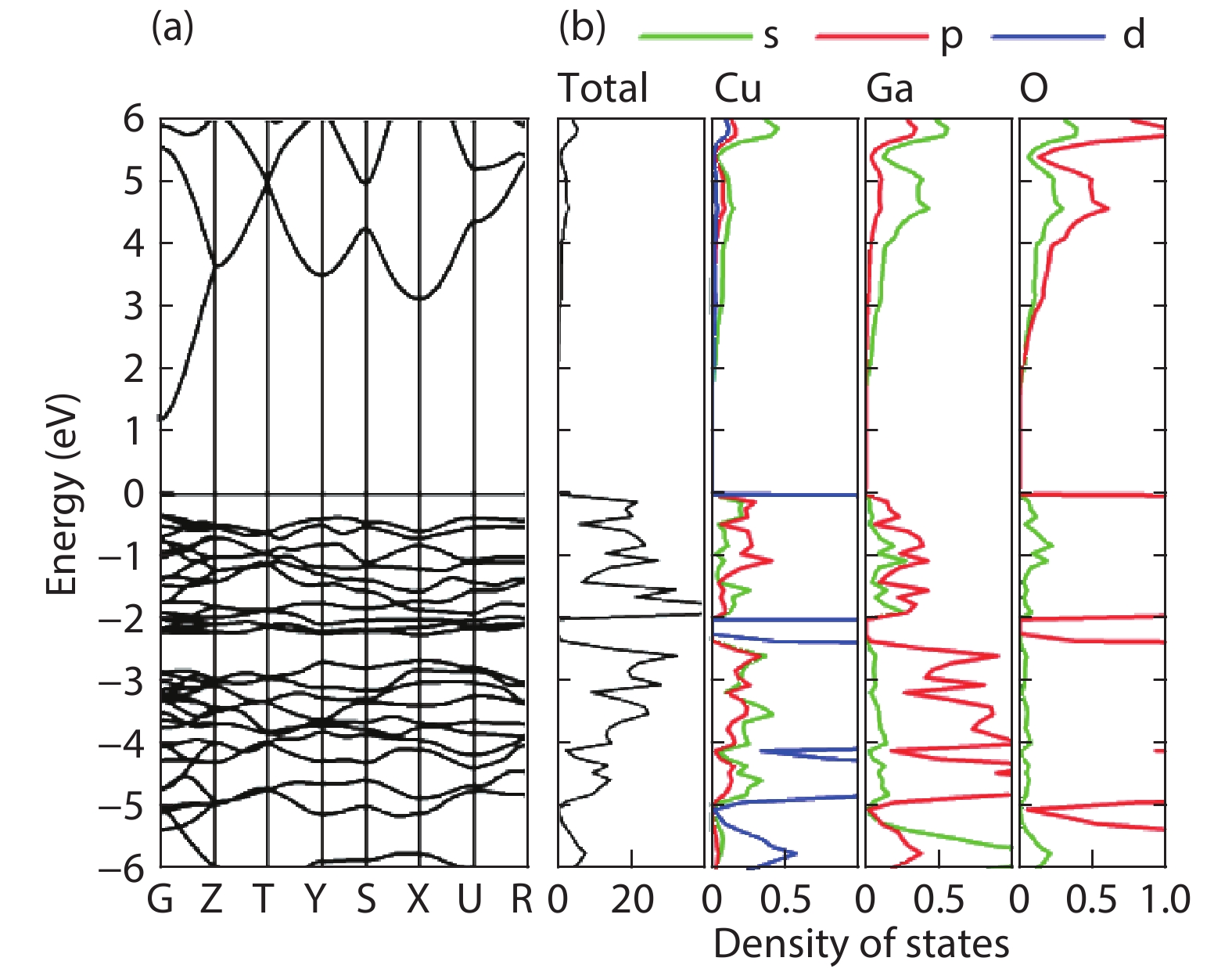
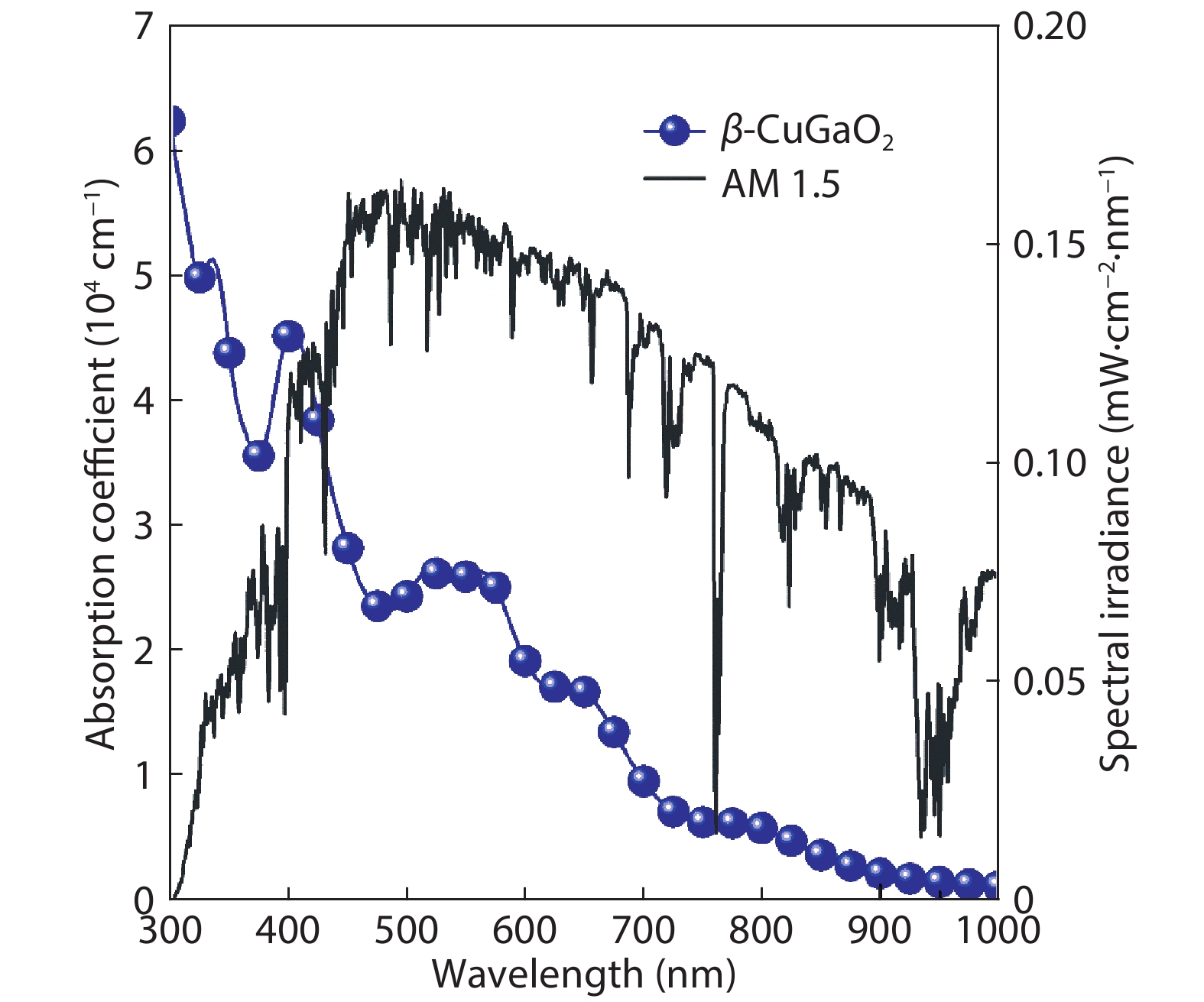
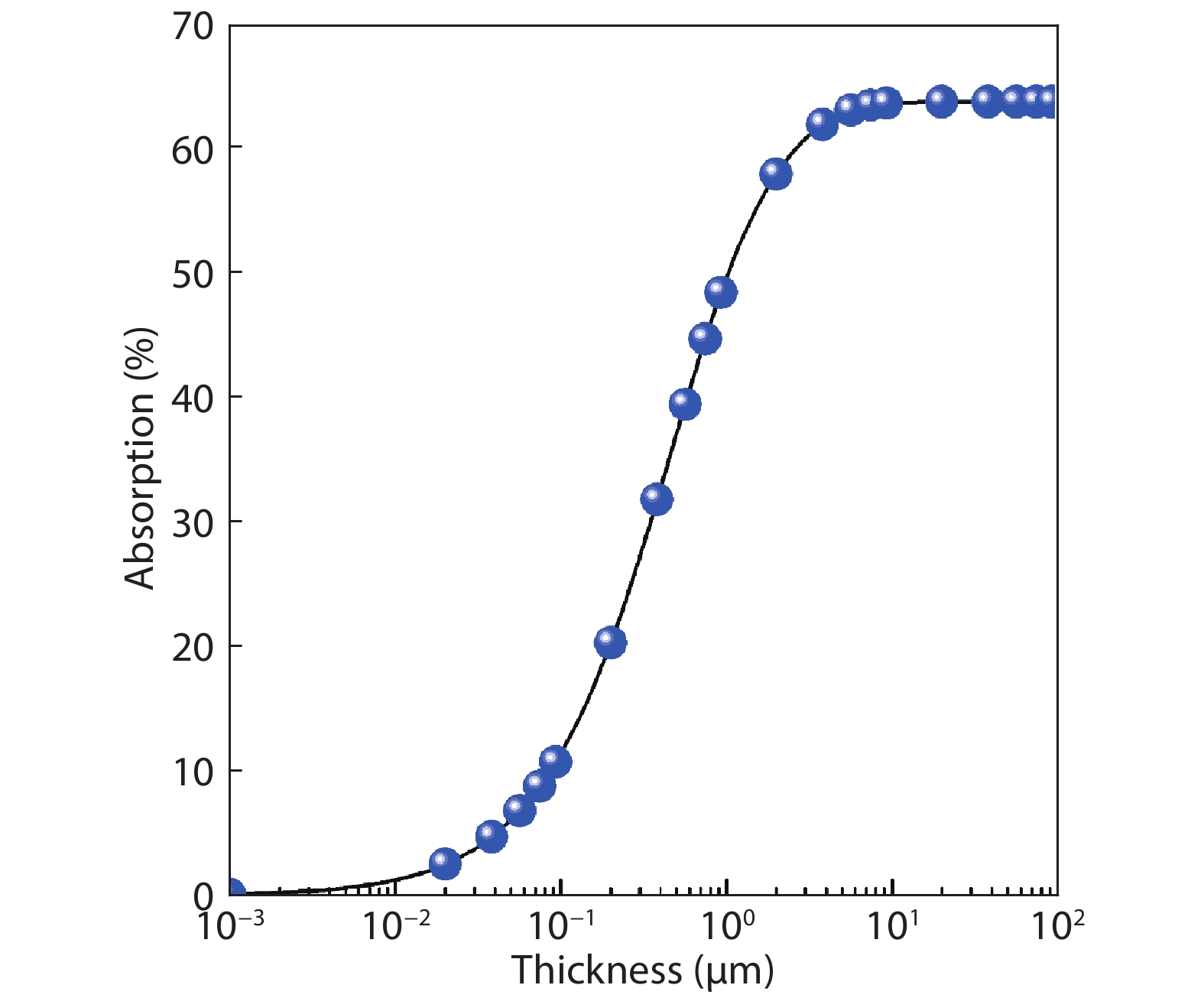
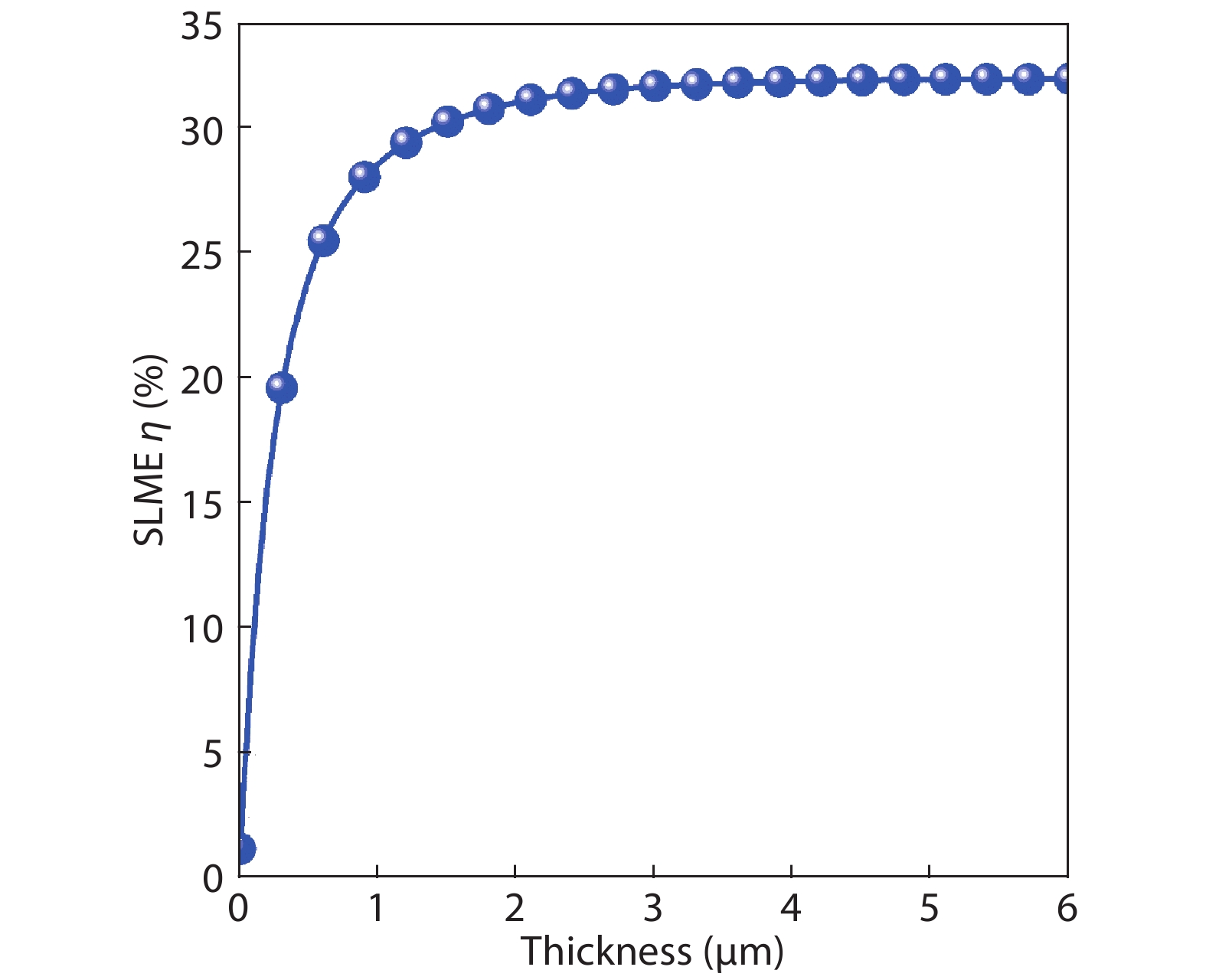
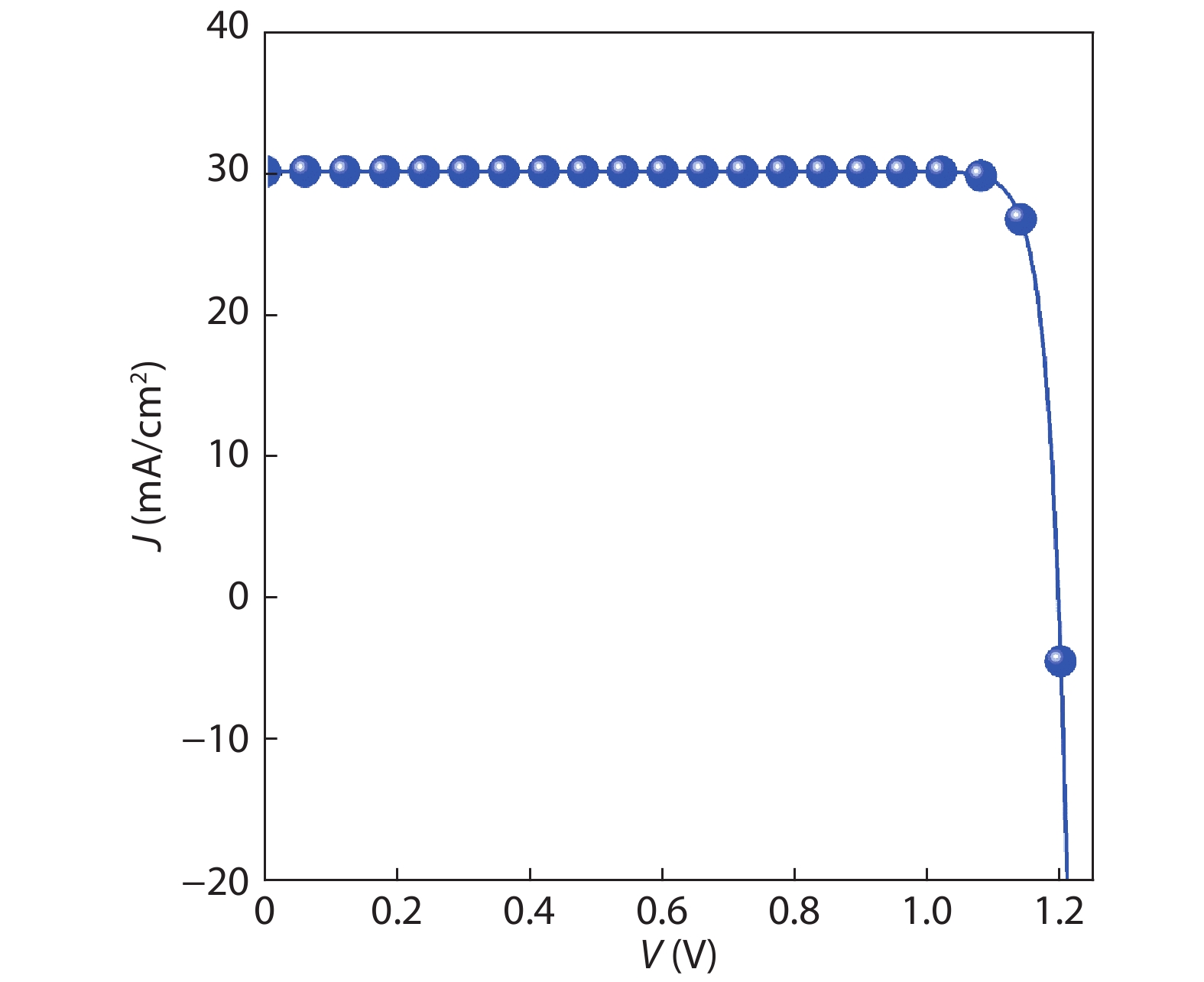
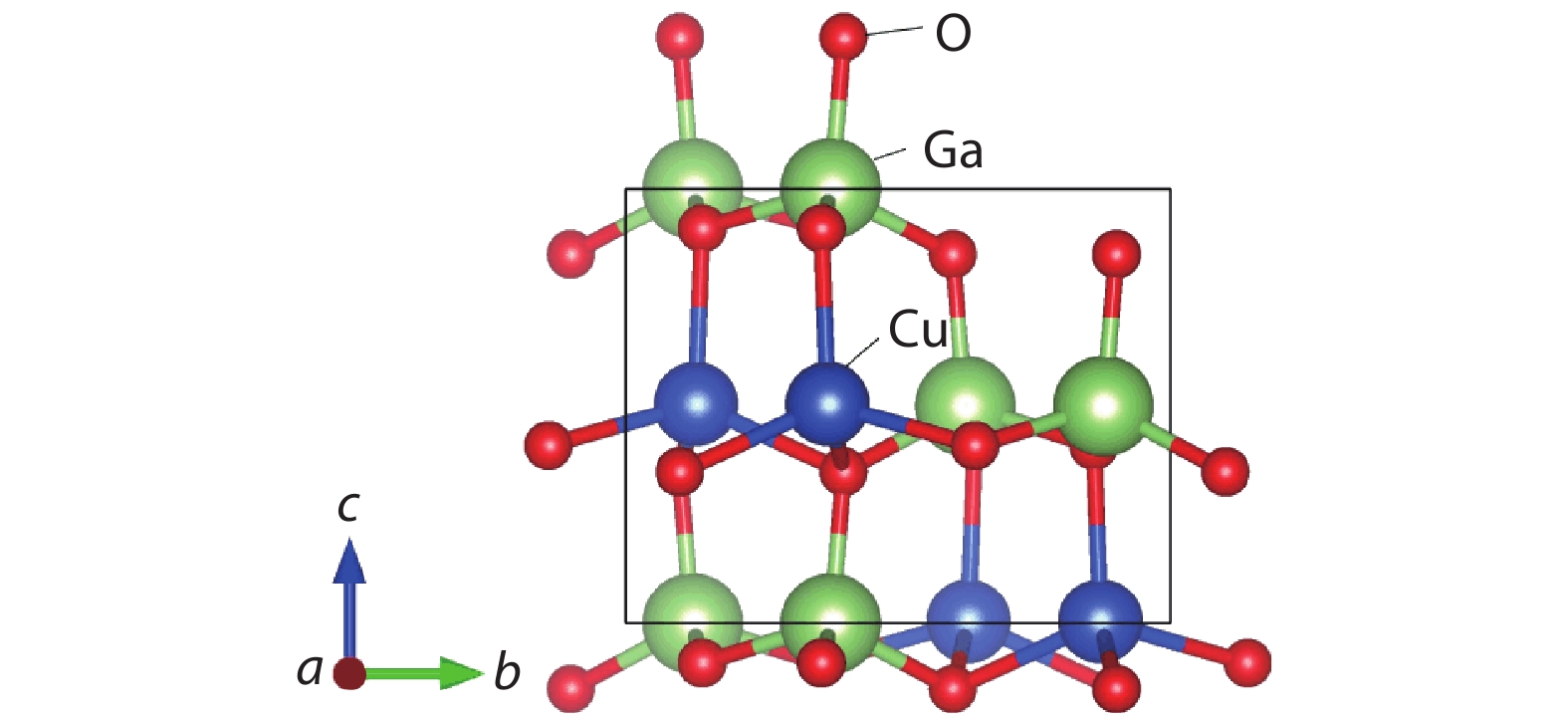
Based on the density functional theory, the energy band and electronic structure of β-CuGaO2 are calculated by the modified Becke-Johnson plus an on-site Coulomb U (MBJ + U) approach in this paper. The calculated results show that the band gap value of β-CuGaO2 obtained by the MBJ + U approach is close to the experimental value. The calculated results of electronic structure indicate that the main properties of the material are determined by the bond between Cu-3d and O-2p energy levels near the valence band of β-CuGaO2, while a weak anti-bond combination is formed mainly by the O-2p energy level and Ga-4s energy level near the bottom of the conduction band of β-CuGaO2. The β-CuGaO2 thin film is predicted to hold excellent photovoltaic performance by analysis of the spectroscopic limited maximum efficiency (SLME) method. At the same time, the calculated maximum photoelectric conversion efficiency of the ideal CuGaO2 solar cell is 32.4%. Relevant conclusions can expand β-CuGaO2 photovoltaic applications. -
References
[1] Ellmer K. Past achievements and future challenges in the development of optically transparent electrodes. Nat Photonics, 2012, 6(12), 809 doi: 10.1038/nphoton.2012.282[2] Minami T. Transparent conducting oxide semiconductors for transparent electrodes. Semicond Sci Tech, 2005, 20(4), S35 doi: 10.1088/0268-1242/20/4/004[3] Klingshirn C. The luminescence of ZnO under high one- and two-quantum excitation. Phys Status Solidi B, 1975, 71(2), 547 doi: 10.1002/pssb.2220710216[4] Tang H, Prasad K, Sanjines R, et al. Electrical and optical properties of TiO2 anatase thin films. J Appl Phys, 1994, 75(4), 2042 doi: 10.1063/1.356306[5] Baumeister P W. Optical absorption of cuprous oxide. Phys Rev, 1961, 121(2), 359 doi: 10.1103/PhysRev.121.359[6] Omata T, Nagatani H, Suzuki I, et al. Wurtzite-derived ternary I–III–O2 semiconductors. Sci Tech Adv Mater, 2015, 16(2), 024902 doi: 10.1088/1468-6996/16/2/024902[7] Omata T, Nagatani H, Suzuki I, et al. Wurtzite CuGaO2: A new direct and narrow band gap oxide semiconductor applicable as a solar cell absorber. J Am Chem Soc, 2014, 136(9), 3378 doi: 10.1021/ja501614n[8] Song S, Kim D, Jang H M, et al. β-CuGaO2 as a strong candidate material for efficient ferroelectric photovoltaics. Chem Mater, 2017, 29(17), 7596 doi: 10.1021/acs.chemmater.7b03141[9] Berglund C N, Braun H J. Optical absorption in single-domain ferroelectric barium titanate. Phys Rev, 1967, 164(2), 790 doi: 10.1103/PhysRev.164.790[10] Ji W, Yao K, Liang Y C. Bulk photovoltaic effect at visible wavelength in epitaxial ferroelectric BiFeO3 thin films. Adv Mater, 2010, 22(15), 1763 doi: 10.1002/adma.200902985[11] Okumura H, Sato K, Kakeshita T. Electronic structure, defect formation energy, and photovoltaic properties of wurtzite-derived CuGaO2. J Appl Phys, 2018, 123(16), 161584 doi: 10.1063/1.5011087[12] Wang L, Maxisch T, Ceder G. Oxidation energies of transition metal oxides within the GGA + U framework. Phys Rev B, 2006, 73(19), 195107 doi: 10.1103/PhysRevB.73.195107[13] Suzuki I, Nagatani H, Kita M, et al. First principles calculations of ternary wurtzite β-CuGaO2. J Appl Phys, 2016, 119(9), 095701 doi: 10.1063/1.4942619[14] Heyd J, Scuseria G E, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys, 2003, 118(18), 8207 doi: 10.1063/1.1564060[15] Shishkin M, Kresse G. Implementation and performance of the frequency-dependent GW method within the PAW framework. Phys Rev B, 2006, 74(3), 035101 doi: 10.1103/physrevb.74.035101[16] Hafner J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J Comput Chem, 2008, 29(13), 2044 doi: 10.1002/jcc.21057[17] Yu L, Zunger A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys Rev Lett, 2012, 108(6), 068701 doi: 10.1103/PhysRevLett.108.068701[18] Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci, 1996, 6(1), 15 doi: 10.1016/0927-0256(96)00008-0[19] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B, 1999, 59, 1758 doi: 10.1103/PhysRevB.59.1758[20] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77, 3865 doi: 10.1103/PhysRevLett.77.3865[21] Liechtenstein A I, Anisimov V I, Zaanen J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys Rev B, 1995, 52(8), R5467 doi: 10.1103/PhysRevB.52.R5467[22] Becke A D, Johnson E R. A simple effective potential for exchange. J Chem Phys, 2006, 124, 221101 doi: 10.1063/1.2213970[23] Tran F, Blaha P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys Rev Lett, 2009, 102(22), 226401 doi: 10.1103/PhysRevLett.102.226401[24] Zhang Y, Wang Y, Xi L, et al. Electronic structure of antifluorite Cu2X (X = S, Se, Te) within the modified Becke-Johnson potential plus an on-site Coulomb U. J Chem Phys, 2014, 140(7), 074702 doi: 10.1063/1.4865257[25] Shockley W, Queisser H J. Detailed balance limit of efficiency of p-n junction solar cells. J Appl Phys, 1961, 32(3), 510 doi: 10.1063/1.1736034[26] Huang X, Paudel T R, Dong S, et al. Hexagonal rare-earth manganites as promising photovoltaics and light polarizers. Phys Rev B, 2015, 92(12), 125201 doi: 10.1103/PhysRevB.92.125201[27] Green M A, Emery K, Hishikawa Y, et al. Solar cell efficiency tables (Version 45). Prog Photovolt: Res Appl, 2015, 23(1), 1 doi: 10.1002/pip.2573 -
Proportional views





 DownLoad:
DownLoad: