| Citation: |
Jian Zheng, Dajun Shu. Regulation of surface properties of photocatalysis material TiO2 by strain engineering[J]. Journal of Semiconductors, 2020, 41(9): 091703. doi: 10.1088/1674-4926/41/9/091703
****
J Zheng, D J Shu, Regulation of surface properties of photocatalysis material TiO2 by strain engineering[J]. J. Semicond., 2020, 41(9): 091703. doi: 10.1088/1674-4926/41/9/091703.
|
Regulation of surface properties of photocatalysis material TiO2 by strain engineering
DOI: 10.1088/1674-4926/41/9/091703
More Information
-
Abstract
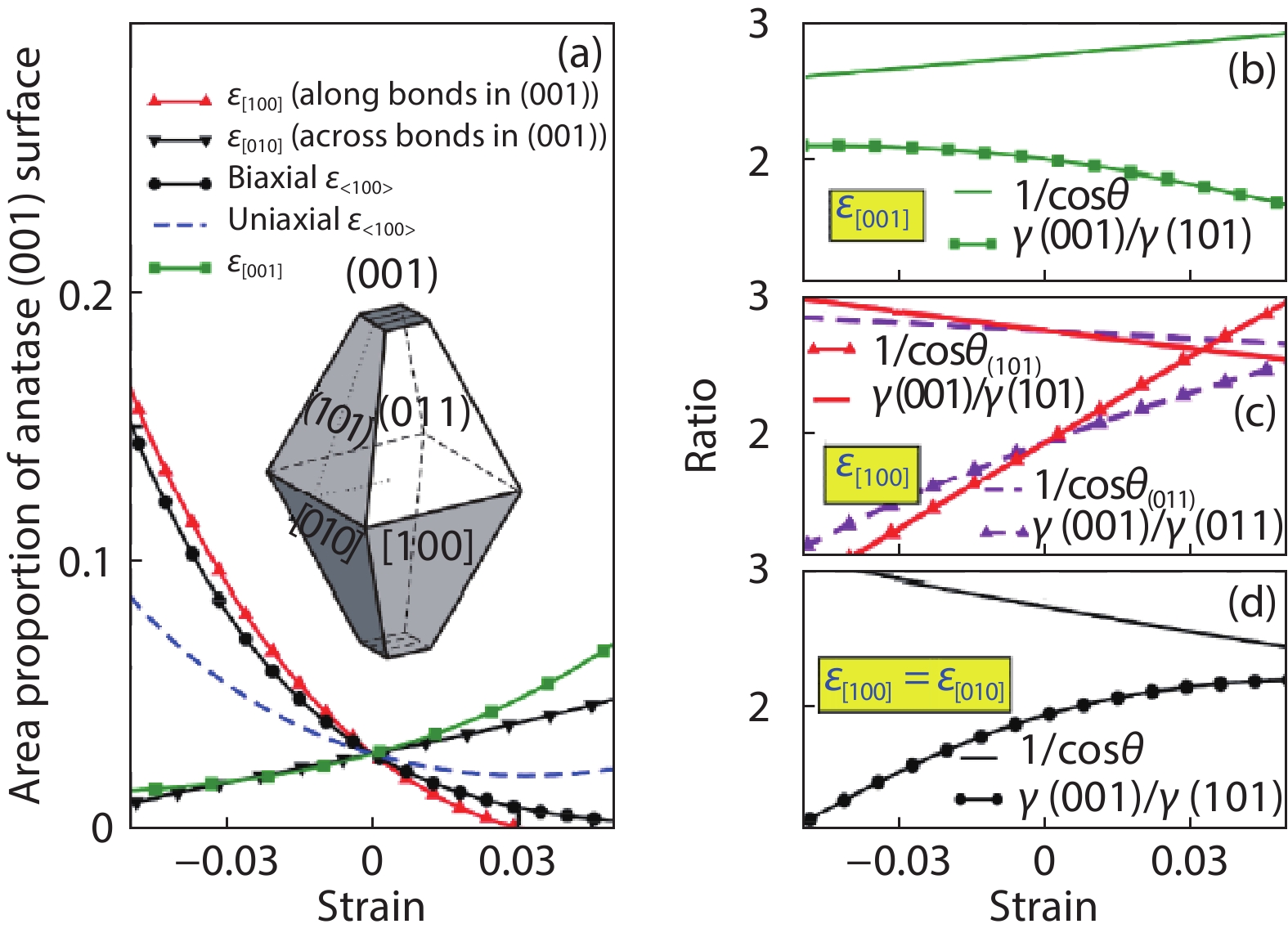
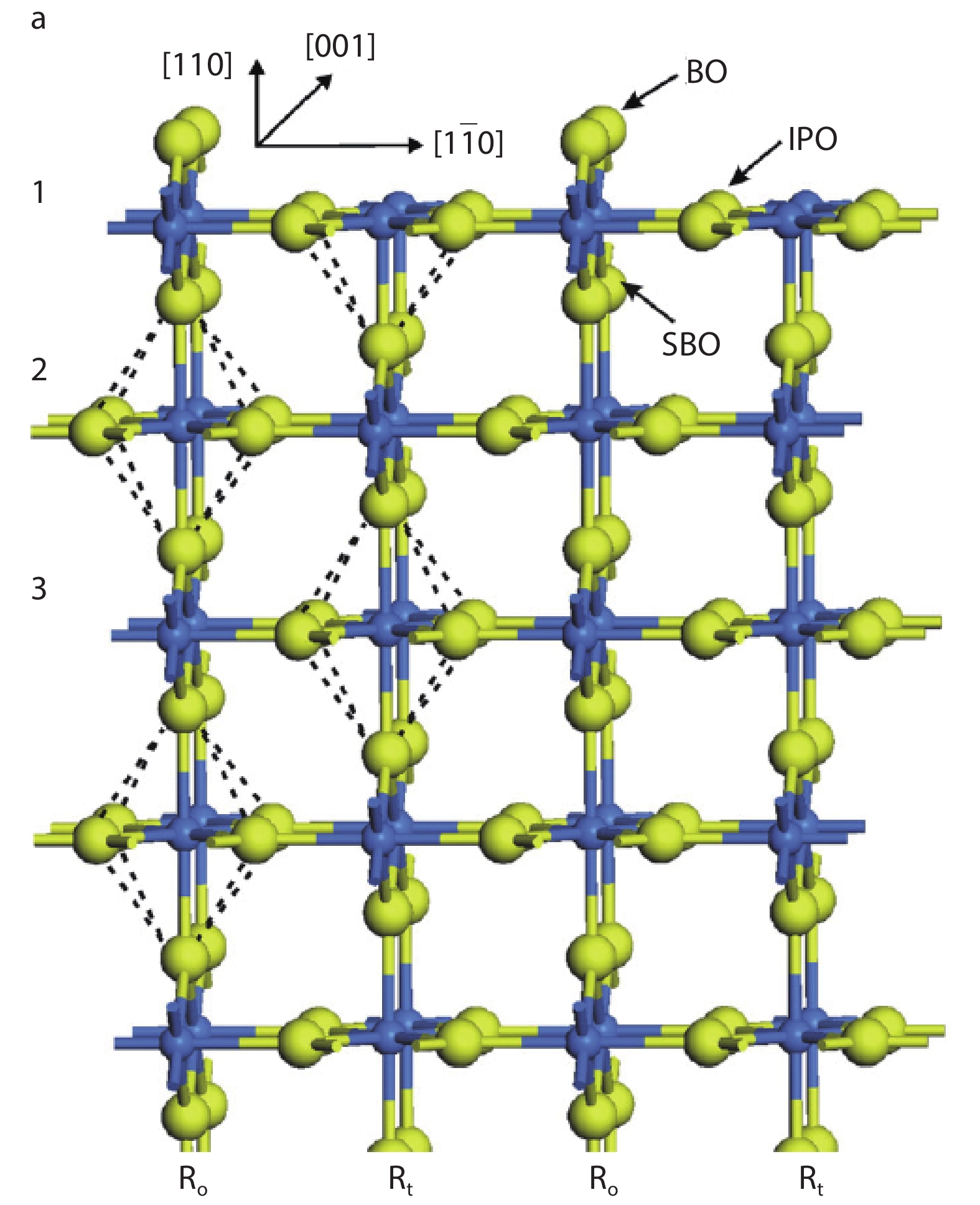
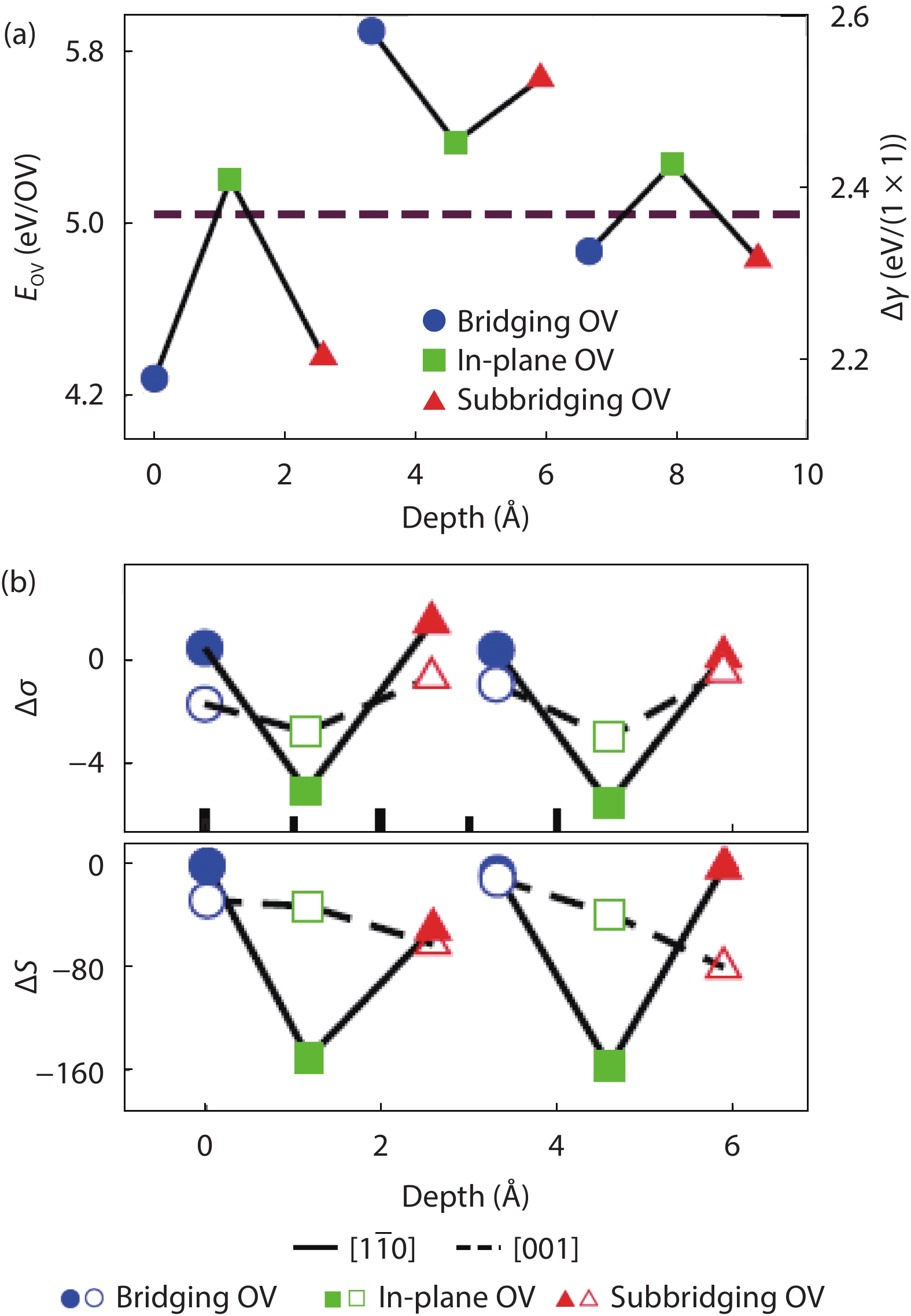
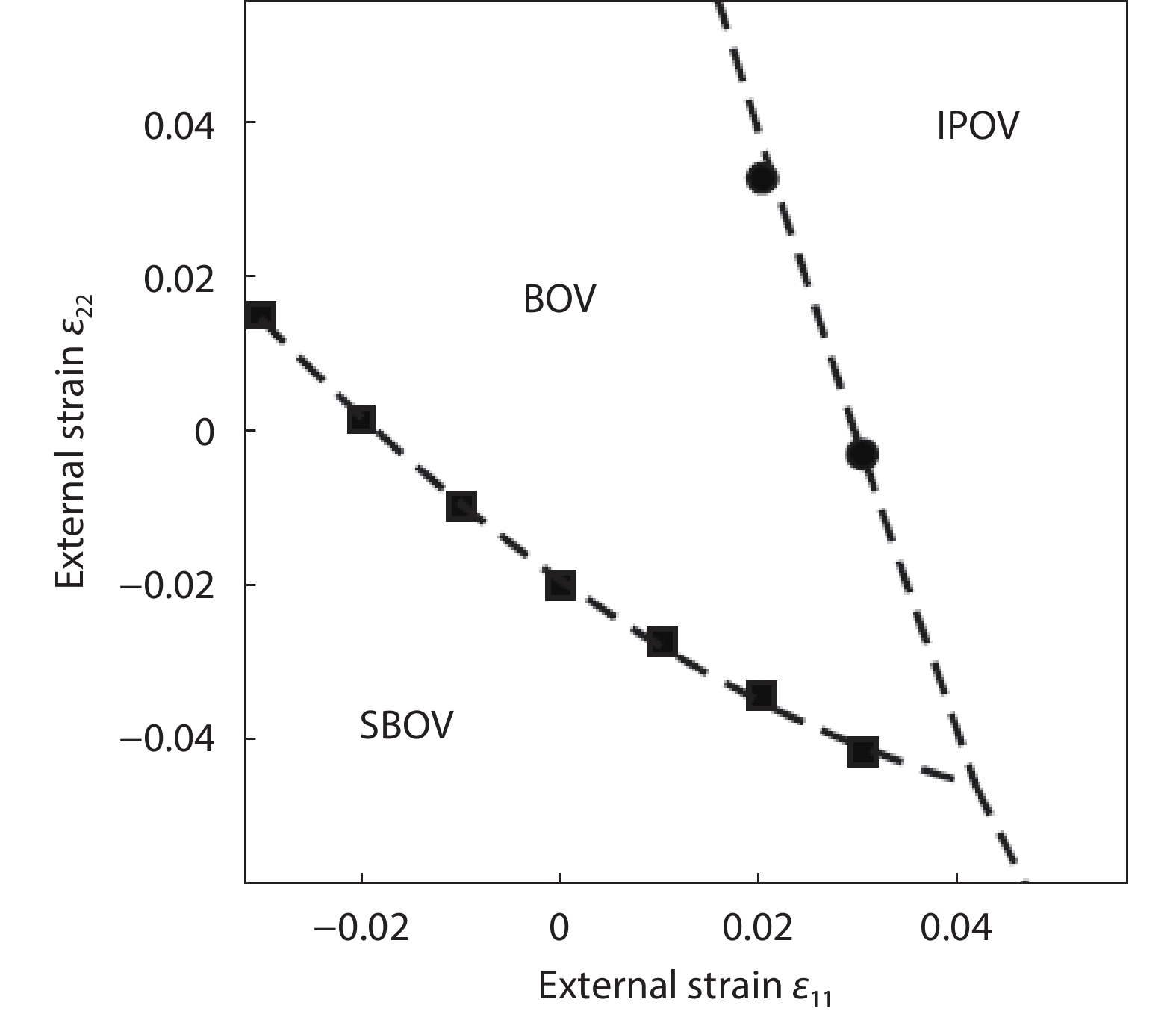
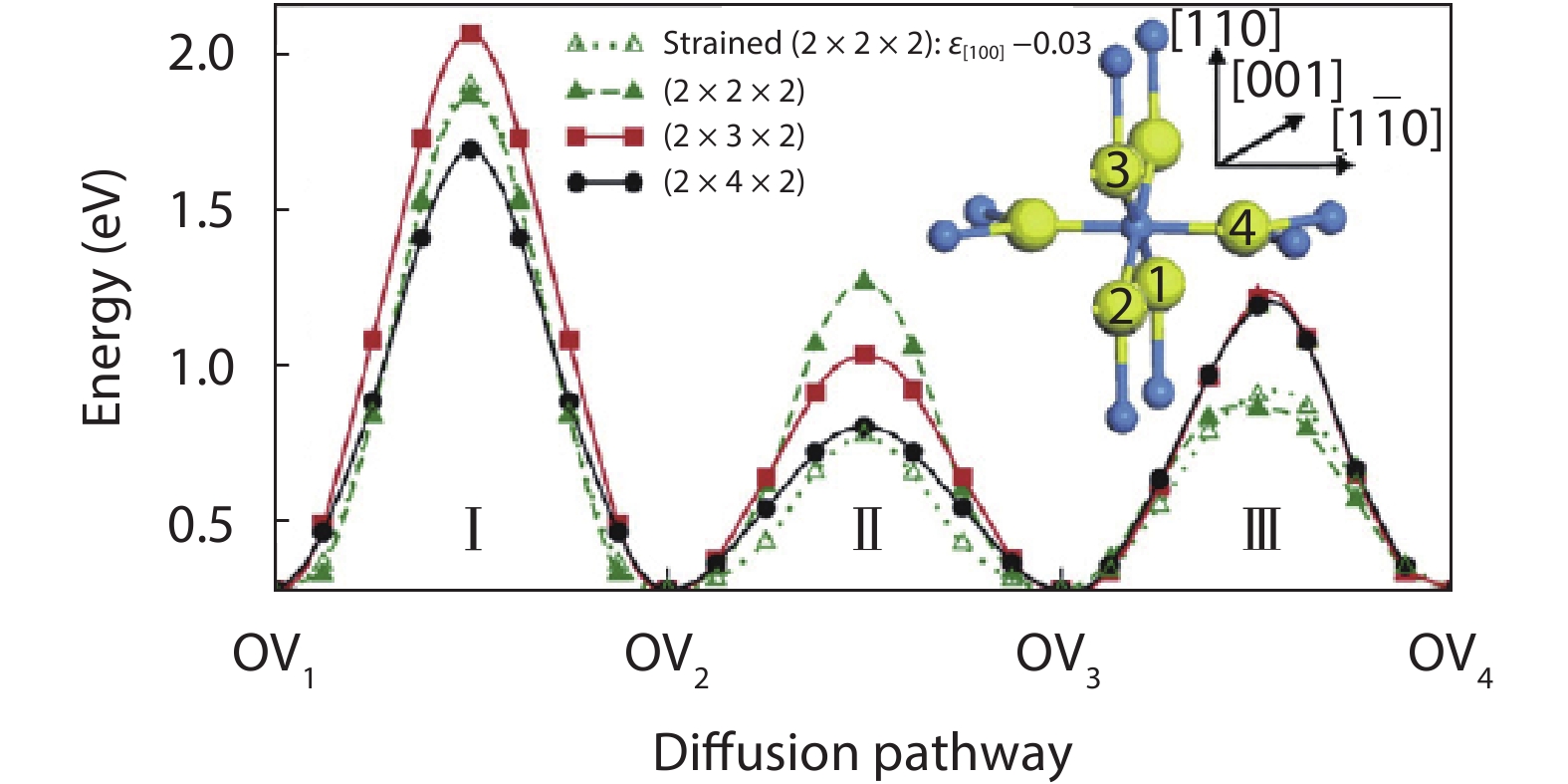
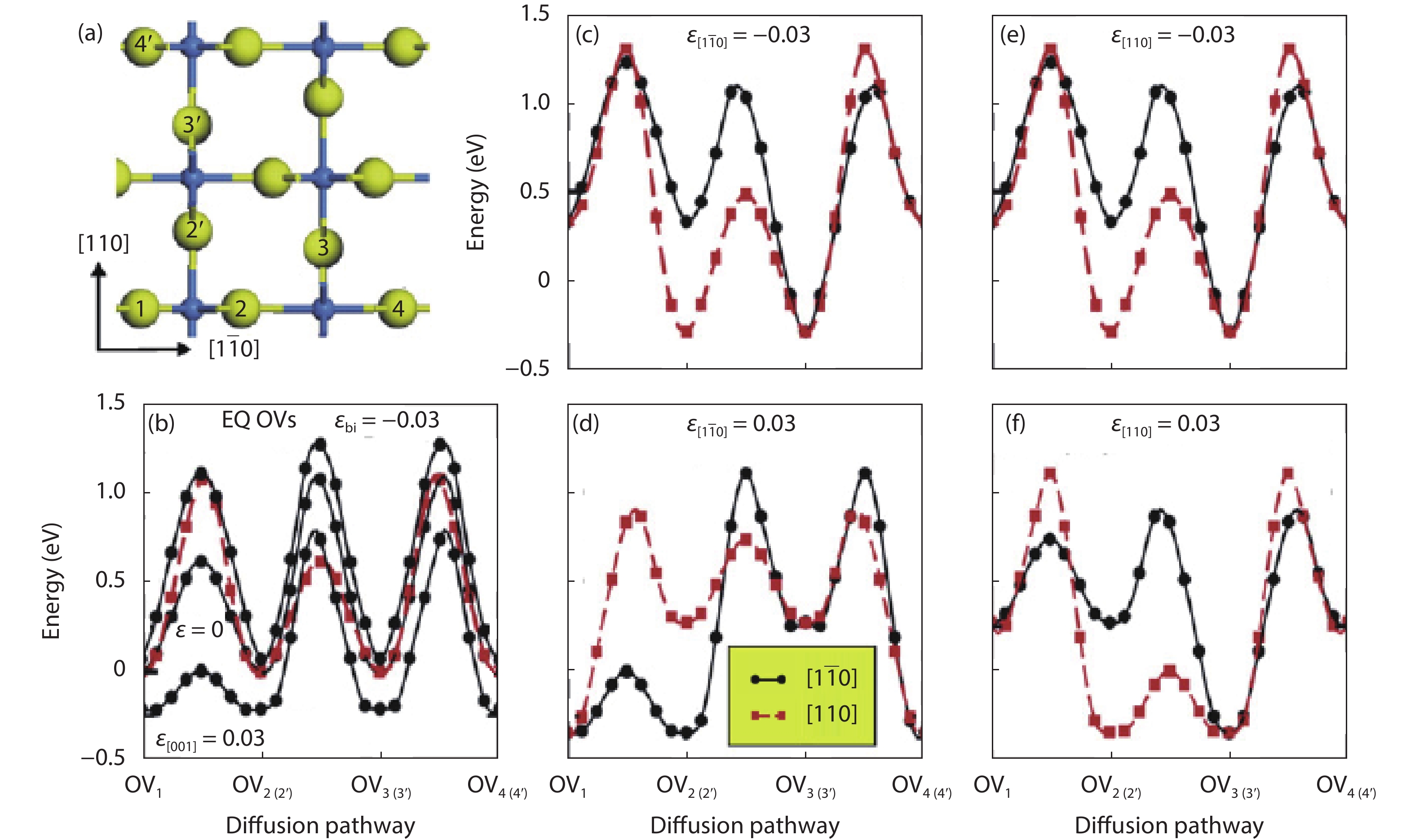
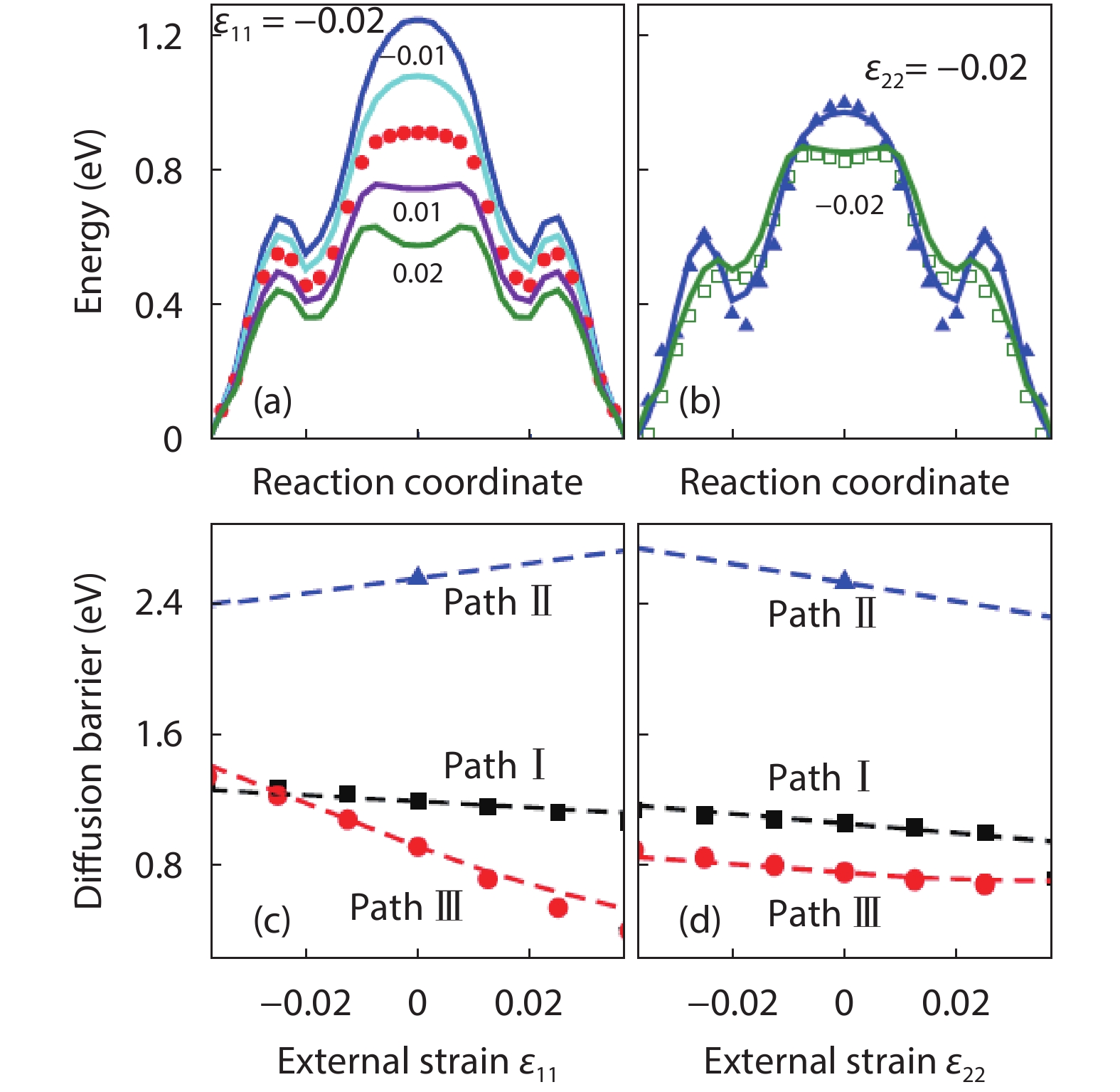
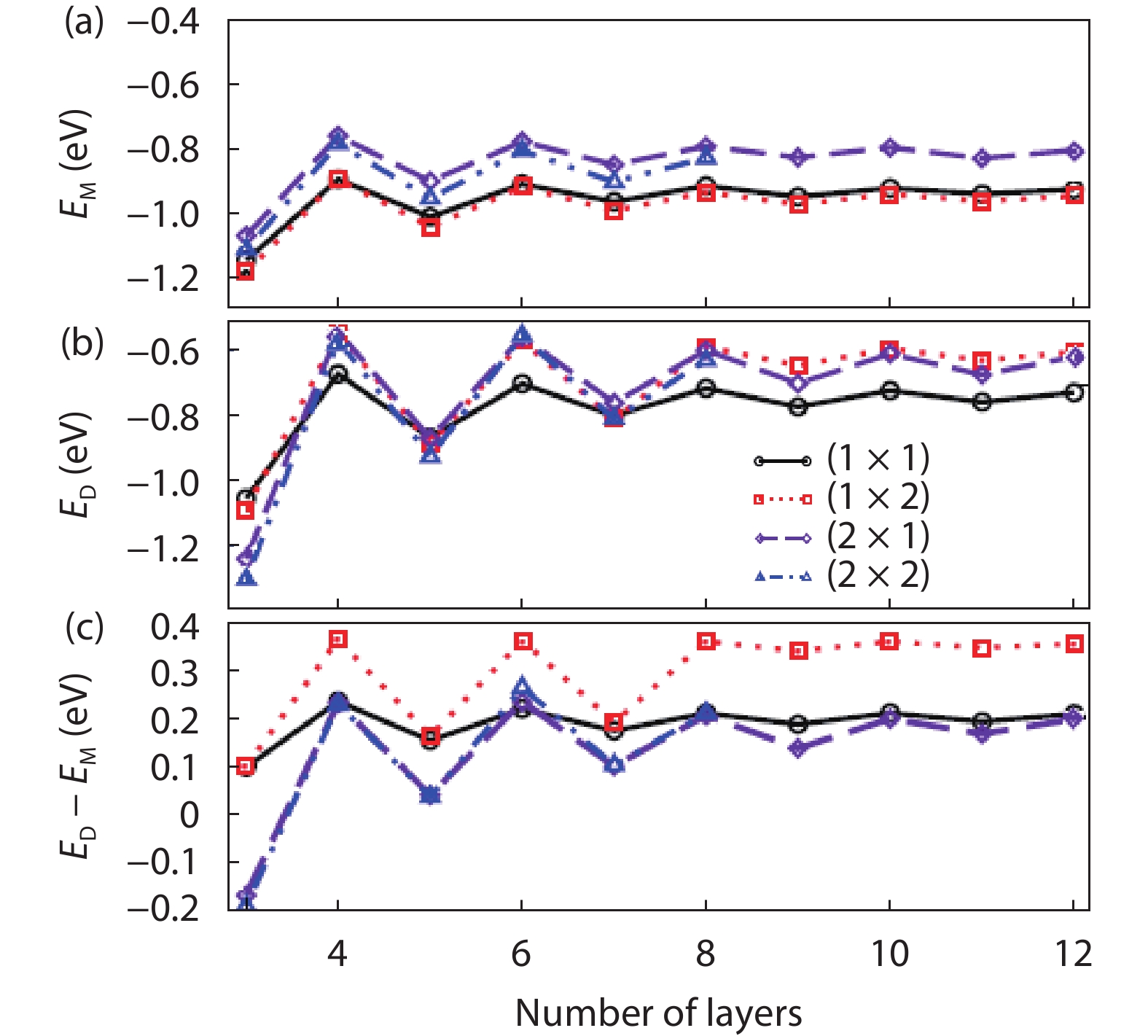
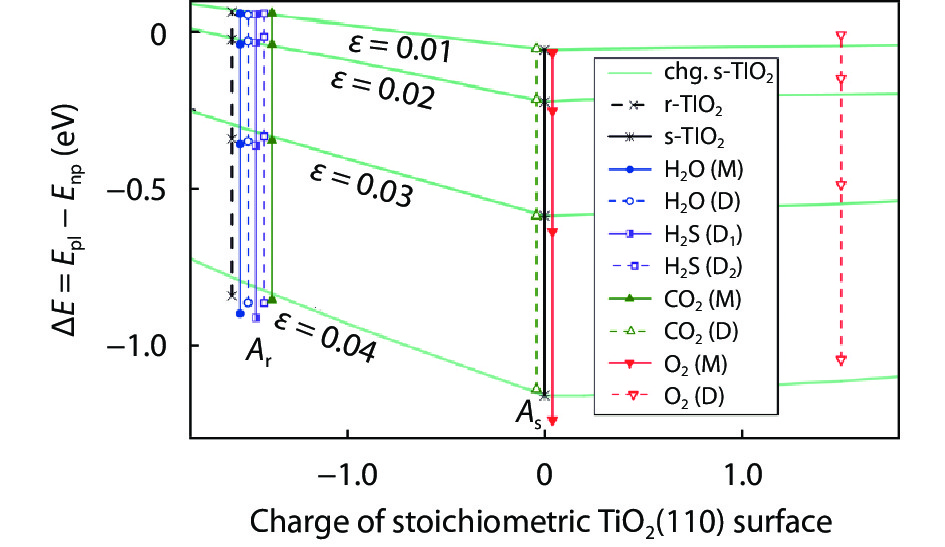
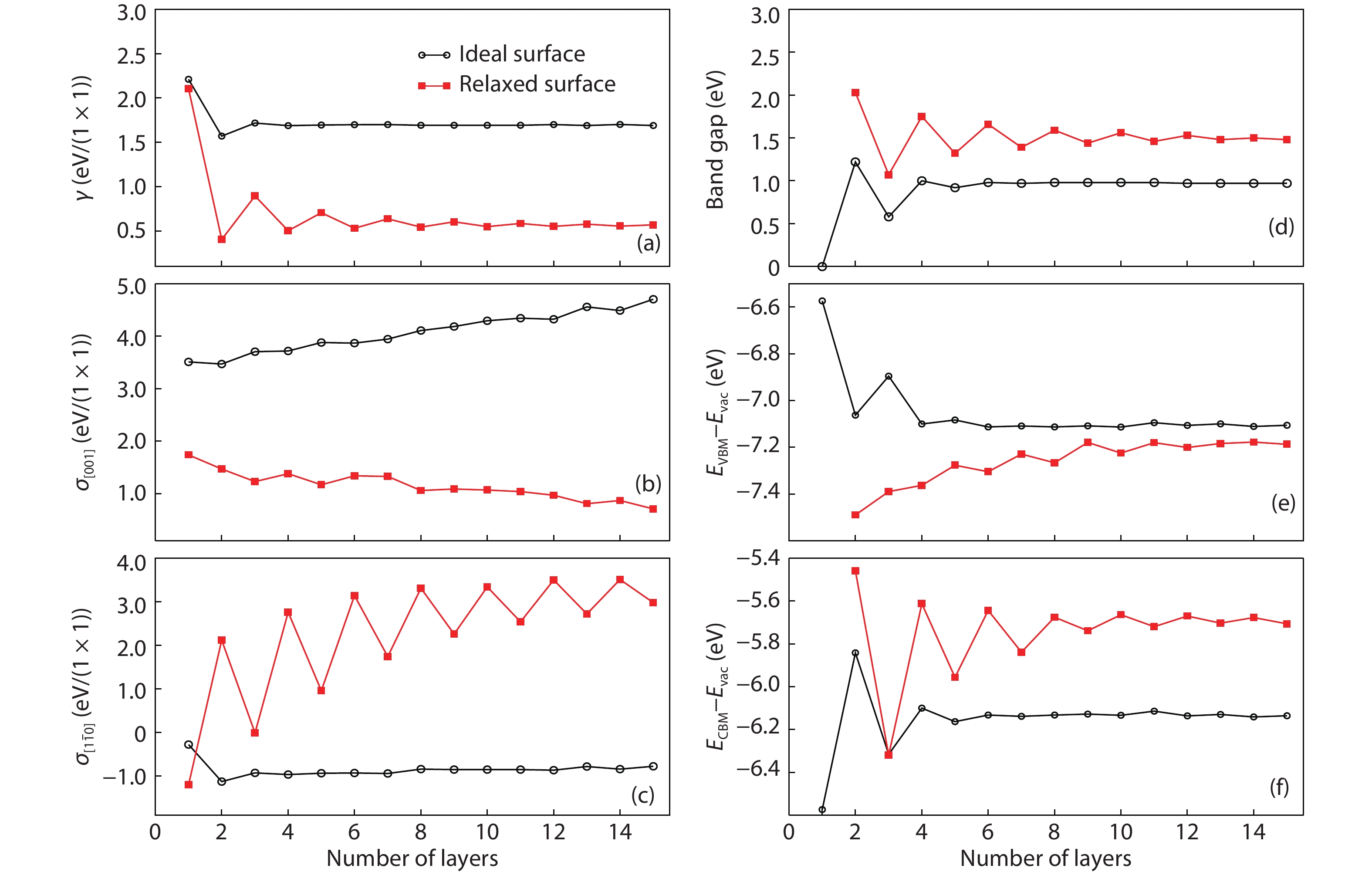
As a promising photocatalysis material, TiO2 has long been studied by experimental and theoretical methods. The external strain could affect the catalytic reactivity of TiO2 significantly due to the difference in surface elastic properties of different surface structures with different surface adsorption or defects. This article reviews our recent work by using density function theory calculations on the effect of strain on the TiO2 surface properties, including surface relative stability, surface defects, surface adsorption and dissociation.-
Keywords:
- semiconductor theory,
- material,
- thin film
-
References
[1] Asahi R, Morikawa T, Ohwaki T, et al. Visible-light photocatalysis in nitrogen-doped titanium oxides. Science, 2001, 293(5528), 269 doi: 10.1126/science.1061051[2] Campbell C T, Parker S C, Starr D E. The effect of size-dependent nanoparticle energetics on catalyst sintering. Science, 2002, 298(5594), 811 doi: 10.1126/science.1075094[3] Bikondoa O, Pang C L, Ithnin R, et al. Direct visualization of defect-mediated dissociation of water on TiO2(110). Nat Mater, 2006, 5(3), 189 doi: 10.1038/nmat1592[4] Gratzel M. Photoelectrochemical cells. Nature, 2001, 414(6861), 338 doi: 10.1038/35104607[5] Lu G, Linsebigler A, Yates J T. Photooxidation of ch3cl on TiO2(110) — a mechanism not involving H2O. J Phys Chem, 1995, 99(19), 7626 doi: 10.1021/j100019a049[6] Pan X Y, Yang M Q, Fu X Z, et al. Defective TiO2 with oxygen vacancies: Synthesis, properties and photocatalytic applications. Nanoscale, 2013, 5(9), 3601 doi: 10.1039/c3nr00476g[7] Yang B, Liu F, Lagally M G. Local strain-mediated chemical potential control of quantum dot self-organization in heteroepitaxy. Phys Rev Lett, 2004, 92(2), 4 doi: 10.1103/PhysRevLett.92.025502[8] Lu G H, Cuma M, Liu F. First-principles study of strain stabilization of Ge(105) facet on Si(001). Phys Rev B, 2005, 72(12), 6 doi: 10.1103/PhysRevB.72.125415[9] Yin W J, Chen S Y, Yang J H, et al. Effective band gap narrowing of anatase TiO2 by strain along a soft crystal direction. Appl Phys Lett, 2010, 96(22), 3 doi: 10.1063/1.3430005[10] Shu D J, Ge S T, Wang M, et al. Interplay between external strain and oxygen vacancies on a rutile TiO2(110) surface. Phys Rev Lett, 2008, 101(11), 4 doi: 10.1103/PhysRevLett.101.116102[11] Wang Z W, Shu D J, Wang M, et al. Diffusion of oxygen vacancies on a strained rutile TiO2(110) surface. Phys Rev B, 2010, 82(16), 7 doi: 10.1103/PhysRevB.82.165309[12] Wang Z W, Shu D J, Wang M, et al. Strain effect on diffusion properties of oxygen vacancies in bulk and subsurface of rutile TiO2. Surf Sci, 2012, 606(3/4), 186 doi: 10.1016/j.susc.2011.09.014[13] Jia L, Shu D J, Wang M. Tuning the area percentage of reactive surface of TiO2 by strain engineering. Phys Rev Lett, 2012, 109(15), 5 doi: 10.1103/PhysRevLett.109.156104[14] Yang L, Shu D J, Li S C, et al. Influence of strain on water adsorption and dissociation on rutile TiO2(110) surface. Phys Chem Chem Phys, 2016, 18(22), 14833 doi: 10.1039/c6cp01106c[15] Wang Z W, Shu D J. Intrinsic interaction between in-plane ferroelectric polarization and surface adsorption. Phys Chem Chem Phys, 2019, 21(34), 18680 doi: 10.1039/c9cp03286j[16] Shojaee E, Mohammadizadeh M R. First-principles elastic and thermal properties of TiO2: A phonon approach. J Phys Condens Matter, 2010, 22(1), 8 doi: 10.1088/0953-8984/22/1/015401[17] Sato H, Ono K, Sasaki T, et al. First-principles study of two-dimensional titanium dioxides. J Phys Chem B, 2003, 107(36), 9824 doi: 10.1021/jp035017t[18] Isaak D G, Carnes J D, Anderson O L, et al. Elasticity of TiO2 rutile to 1800 K. Phys Chem Miner, 1998, 26(1), 31 doi: 10.1007/s002690050158[19] Cammarata R C. Surface and interface stress effects in thin-films. Prog Surf Sci, 1994, 46(1), 1 doi: 10.1016/0079-6816(94)90005-1[20] Vittadini A, Casarin M, Selloni A. Chemistry of and on TiO2-anatase surfaces by dft calculations: a partial review. Theor Chem Acc, 2007, 117(5/6), 663 doi: 10.1007/s00214-006-0191-4[21] Lazzeri M, Vittadini A, Selloni A. Structure and energetics of stoichiometric TiO2 anatase surfaces. Phys Rev B, 2001, 63(15), 9 doi: 10.1103/PhysRevB.63.155409[22] Diebold U, Ruzycki N, Herman G S, et al. One step towards bridging the materials gap: surface studies of TiO2 anatase. Catal Today, 2003, 85(2–4), 93 doi: 10.1016/s0920-5861(03)00378-x[23] Wendt S, Schaub R, Matthiesen J, et al. Oxygen vacancies on TiO2(110) and their interaction with H2O and O2: A combined high-resolution STM and DFT study. Surf Sci, 2005, 598(1–3), 226 doi: 10.1016/j.susc.2005.08.041[24] Thompson T L, Yates J T. Surface science studies of the photoactivation of TiO2 – new photochemical processes. Chem Rev, 2006, 106(10), 4428 doi: 10.1021/cr050172k[25] Yim C M, Pang C L, Thornton G. Oxygen vacancy origin of the surface band-gap state of TiO2(110). Phys Rev Lett, 2010, 104(3), 4 doi: 10.1103/PhysRevLett.104.036806[26] Diebold U, Lehman J, Mahmoud T, et al. Intrinsic defects on a TiO2(110)(1x1) surface and their reaction with oxygen: A scanning tunneling microscopy study. Surf Sci, 1998, 411(1/2), 137 doi: 10.1016/s0039-6028(98)00356-2[27] Wahlstrom E, Lopez N, Schaub R, et al. Bonding of gold nanoclusters to oxygen vacancies on rutile TiO2(110). Phys Rev Lett, 2003, 90(2), 4 doi: 10.1103/PhysRevLett.90.026101[28] Schaub R, Wahlstrom E, Ronnau A, et al. Oxygen-mediated diffusion of oxygen vacancies on the TiO2(110) surface. Science, 2003, 299(5605), 377 doi: 10.1126/science.1078962[29] Zhang Z R, Rousseau R, Gong J L, et al. Vacancy-assisted diffusion of alkoxy species on rutile TiO2(110). Phys Rev Lett, 2008, 101(15), 4 doi: 10.1103/PhysRevLett.101.156103[30] Kimmel G A, Petrik N G. Tetraoxygen on reduced TiO2(110): Oxygen adsorption and reactions with bridging oxygen vacancies. Phys Rev Lett, 2008, 100(19), 4 doi: 10.1103/PhysRevLett.100.196102[31] Klenov D O, Donner W, Foran B, et al. Impact of stress on oxygen vacancy ordering in epitaxial (La0.5Sr0.5)CoO3-partial derivative thin films. Appl Phys Lett, 2003, 82(20), 3427 doi: 10.1063/1.1575503[32] Kamisaka H, Yamashita K. The surface stress of the (110) and (100) surfaces of rutile 14 and the effect of water adsorbents. Surf Sci, 2007, 601(21), 4824 doi: 10.1016/j.susc.2007.07.033[33] Hameeuw K, Cantele G, Ninno D, et al. Influence of surface and subsurface defects on the behavior of the rutile TiO2(110) surface. Phys Status Solidi A, 2006, 203(9), 2219 doi: 10.1002/pssa.200566015[34] Bredow T, Giordano L, Cinquini F, et al. Electronic properties of rutile TiO2 ultrathin films: Odd-even oscillations with the number of layers. Phys Rev B, 2004, 70(3), 6 doi: 10.1103/PhysRevB.70.035419[35] Lee C, Ghosez P, Gonze X. Lattice-dynamics and dielectric-properties of incipient ferroelectric TiO2 rutile. Phys Rev B, 1994, 50(18), 13379 doi: 10.1103/PhysRevB.50.13379[36] Parker R A. Static dielectric constant of rutile (TiO2), 1.6–1060 °K. Phys Rev, 1961, 124(6), 1719 doi: 10.1103/PhysRev.124.1719[37] Trayler J G, Smith H G, Nicklow R M, et al. Lattice dynamics of rutile. Phys Rev B, 1971, 3(10), 3457 doi: 10.1103/PhysRevB.3.3457 -
Proportional views





 DownLoad:
DownLoad: