| Citation: |
Xinyu Liu, Logan Riney, Josue Guerra, William Powers, Jiashu Wang, Jacek K. Furdyna, Badih A. Assaf. Colossal negative magnetoresistance from hopping in insulating ferromagnetic semiconductors[J]. Journal of Semiconductors, 2022, 43(11): 112502. doi: 10.1088/1674-4926/43/11/112502
****
X Y Liu, L Riney, J Guerra, W Powers, J S Wang, J K Furdyna, B A Assaf. Colossal negative magnetoresistance from hopping in insulating ferromagnetic semiconductors[J]. J. Semicond, 2022, 43(11): 112502. doi: 10.1088/1674-4926/43/11/112502
|
Colossal negative magnetoresistance from hopping in insulating ferromagnetic semiconductors
DOI: 10.1088/1674-4926/43/11/112502
More Information
-
Abstract
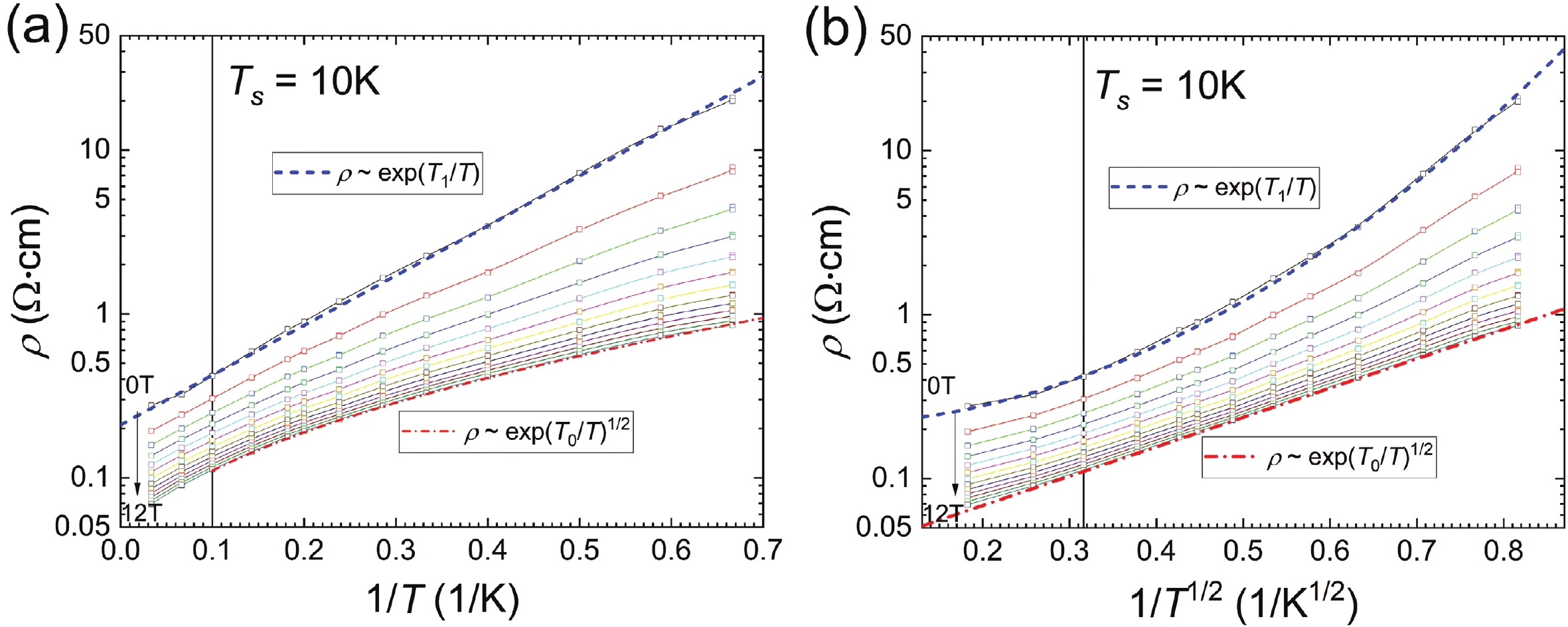
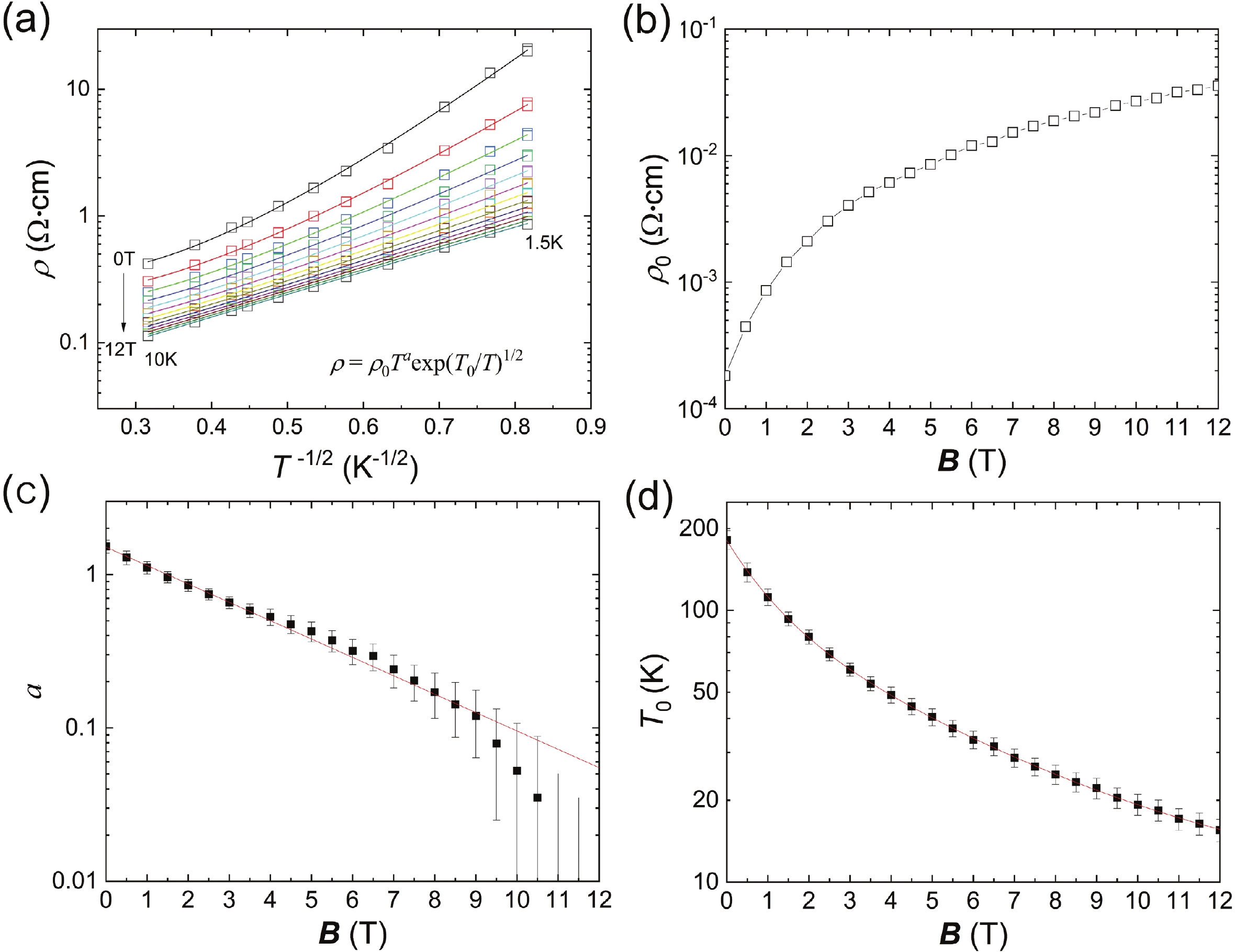
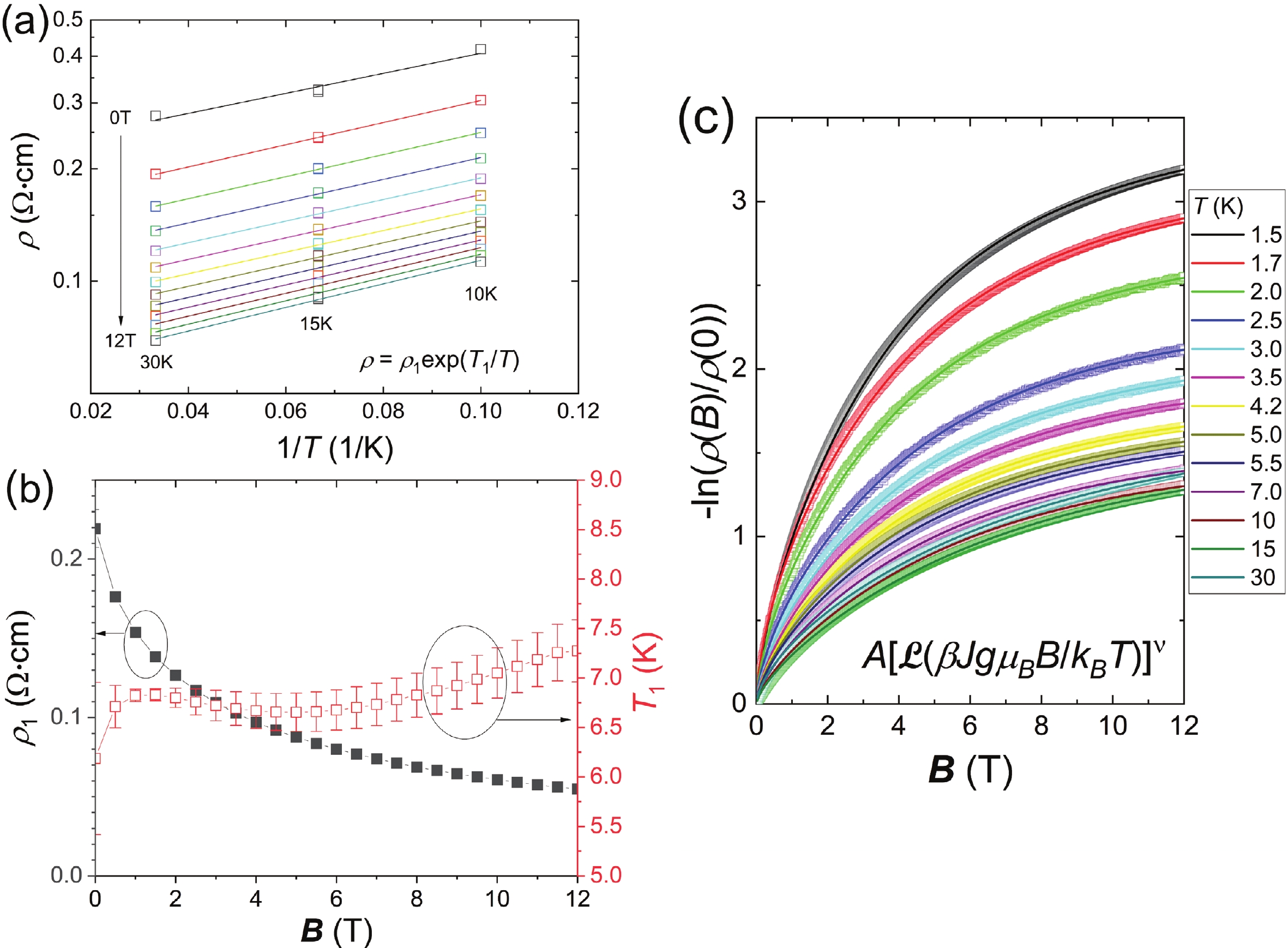
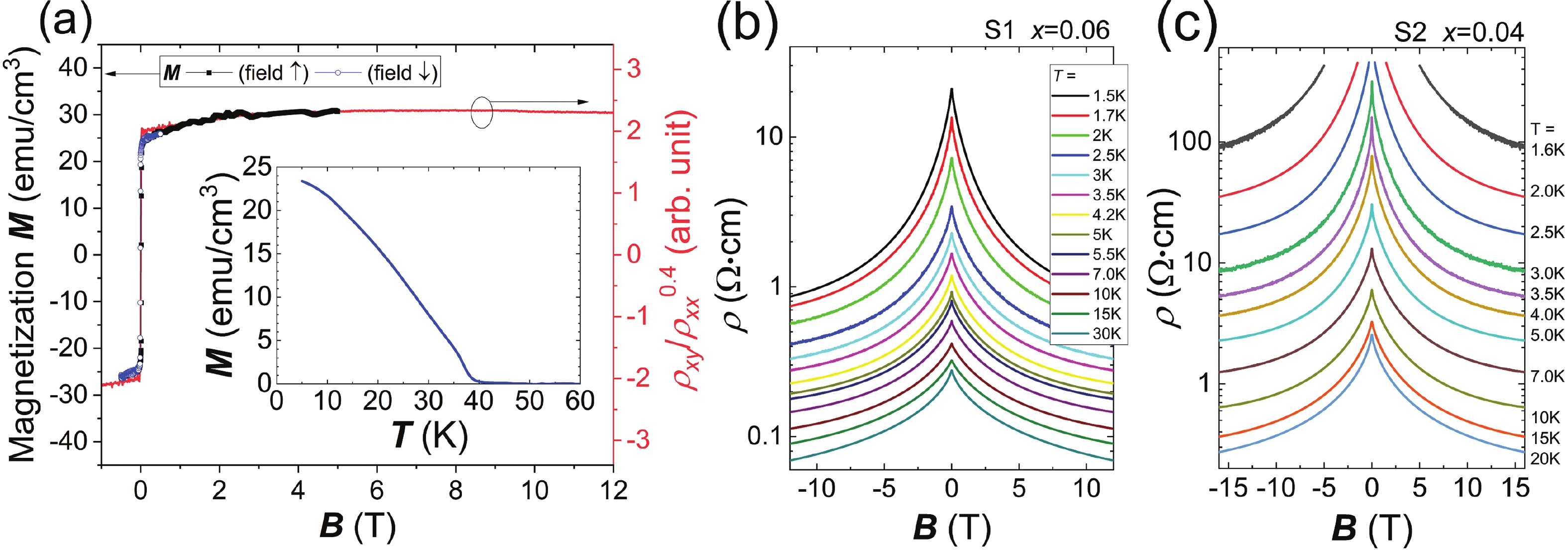
Ferromagnetic semiconductor Ga1–xMnxAs1–yPy thin films go through a metal–insulator transition at low temperature where electrical conduction becomes driven by hopping of charge carriers. In this regime, we report a colossal negative magnetoresistance (CNMR) coexisting with a saturated magnetic moment, unlike in the traditional magnetic semiconductor Ga1–xMnxAs. By analyzing the temperature dependence of the resistivity at fixed magnetic field, we demonstrate that the CNMR can be consistently described by the field dependence of the localization length, which relates to a field dependent mobility edge. This dependence is likely due to the random environment of Mn atoms in Ga1–xMnxAs1–yPy which causes a random spatial distribution of the mobility that is suppressed by an increasing magnetic field. -
References
[1] Thouless D J. Electrons in disordered systems and the theory of localization. Phys Rep, 1974, 13, 93 doi: 10.1016/0370-1573(74)90029-5[2] Sondhi S L, Girvin S M, Carini J P, et al. Continuous quantum phase transitions. Rev Mod Phys, 1997, 69, 315 doi: 10.1103/RevModPhys.69.315[3] Mott N F. Conduction in non-crystalline materials. Philos Mag, 1969, 19, 835 doi: 10.1080/14786436908216338[4] Efros A L, Shklovskii B I. Electronic properties of doped semiconductors. Berlin: Springer, 1984[5] Mott N F. Conduction in glasses containing transition metal ions. J Non Cryst Solids, 1968, 1, 1 doi: 10.1016/0022-3093(68)90002-1[6] Efros A L, Shklovskii B I. Coulomb gap and low temperature conductivity of disordered systems. J Phys C, 1975, 8, L49 doi: 10.1088/0022-3719/8/4/003[7] Zhang Y Z, Dai O, Levy M, et al. Probind the coulomb gap in insulating n-type CdSe. Phys Rev Lett, 1990, 64, 2687 doi: 10.1103/PhysRevLett.64.2687[8] Aharony A, Zhang Y, Sarachik M P. Universal crossover in variable range hopping with Coulomb interactions. Phys Rev Lett, 1992, 68, 3900 doi: 10.1103/PhysRevLett.68.3900[9] Viret M, Ranno L, Coey J M D. Colossal magnetoresistance of the variable range hopping regime in the manganites. J Appl Phys, 1997, 81, 4964 doi: 10.1063/1.365013[10] Masarrat A, Bhogra A, Meena R, et al. Enhancement of the thermoelectric properties and transition of conduction mechanism from nearest neighbor to variable range hopping of Ni-doped CoSb3. J Electron Mater, 2022, 51, 3350 doi: 10.1007/s11664-022-09547-1[11] Zhang L J, King I, Nasyedkin K, et al. Coherent hopping transport and giant negative magnetoresistance in epitaxial CsSnBr3. ACS Appl Electron Mater, 2021, 3, 2948 doi: 10.1021/acsaelm.1c00409[12] Xue J H, Huang S Y, Wang J Y, et al. Mott variable-range hopping transport in a MoS2 nanoflake. RSC Adv, 2019, 9, 17885 doi: 10.1039/C9RA03150B[13] Rimal G, Tang J K. Magnetic hard gap due to bound magnetic polarons in the localized regime. Sci Rep, 2017, 7, 42224 doi: 10.1038/srep42224[14] Joung D, Khondaker S I. Efros-Shklovskii variable range hopping in reduced graphene oxide sheets of varying carbon sp2 fraction. Phys Rev B, 2012, 86, 235423 doi: 10.1103/PhysRevB.86.235423[15] Punia R, Kundu R S, Murugavel S, et al. Hopping conduction in bismuth modified zinc vanadate glasses: An applicability of Mott's model. J Appl Phys, 2012, 112, 113716 doi: 10.1063/1.4768898[16] Iye Y, Oiwa A, Endo A, et al. Metal-insulator transition and magnetotransport in III-V compound diluted magnetic semiconductors. Mater Sci Eng B, 1999, 63, 88 doi: 10.1016/S0921-5107(99)00057-4[17] Dong S N, Riney L, Liu X Y, et al. Carrier localization in quaternary Ga1− xMn xAs1− yP y ferromagnetic semiconductor films. Phys Rev Mater, 2021, 5, 014402 doi: 10.1103/PhysRevMaterials.5.014402[18] Liu X Y, Dong S N, Riney L, et al. Crossover behavior of the anomalous Hall effect in Ga1− xMn xAs1− yP y across the metal-insulator transition. Phys Rev B, 2021, 103, 214437 doi: 10.1103/PhysRevB.103.214437[19] Lee H, Chang J, Chongthanaphisut P, et al. Magnetic anisotropy of quaternary GaMnAsP ferromagnetic semiconductor. AIP Adv, 2017, 7, 055809 doi: 10.1063/1.4972856[20] Li X, Liu X Y, Dong S N, et al. Dependence of ferromagnetic properties on phosphorus concentration in Ga1– xMn xAs1– yP y. J Vac Sci Technol B, 2018, 36, 02D104 doi: 10.1116/1.5014055[21] Takeda Y, Ohya S, Pham N H, et al. Direct observation of the magnetic ordering process in the ferromagnetic semiconductor Ga1− xMn xAs via soft X-ray magnetic circular dichroism. J Appl Phys, 2020, 128, 213902 doi: 10.1063/5.0031605[22] Onoda S, Sugimoto N, Nagaosa N. Quantum transport theory of anomalous electric, thermoelectric, and thermal Hall effects in ferromagnets. Phys Rev B, 2008, 77, 165103 doi: 10.1103/PhysRevB.77.165103[23] Wagner P, Gordon I, Trappeniers L, et al. Spin dependent hopping and colossal negative magnetoresistance in epitaxial Nd0.52Sr0.48MnO3 films in fields up to 50 T. Phys Rev Lett, 1998, 81, 3980 doi: 10.1103/PhysRevLett.81.3980[24] Zaránd G, Moca C P, Jankó B. Scaling theory of magnetoresistance in disordered local moment ferromagnets. Phys Rev Lett, 2005, 94, 247202 doi: 10.1103/PhysRevLett.94.247202[25] Oiwa A, Katsumoto S, Endo A, et al. Nonmetal-metal-nonmetal transition and large negative magnetoresistance in (Ga, Mn)As/GaAs. Solid State Commun, 1997, 103, 209 doi: 10.1016/S0038-1098(97)00178-6[26] Yuan Y, Xu C, Hübner R, et al. Interplay between localization and magnetism in (Ga, Mn)As and (In, Mn)As. Phys Rev Mater, 2017, 1, 054401 doi: 10.1103/PhysRevMaterials.1.054401[27] Yakimov A I, Wright T, Adkins C J, et al. Magnetic correlations on the insulating side of the metal-insulator transition in amorphous Si1− xMn x. Phys Rev B, 1995, 51, 16549 doi: 10.1103/PhysRevB.51.16549[28] Yildiz A, Serin N, Serin T, et al. Crossover from nearest-neighbor hopping conduction to Efros–Shklovskii variable-range hopping conduction in hydrogenated amorphous silicon films. Jpn J Appl Phys, 2009, 48, 111203 doi: 10.1143/JJAP.48.111203[29] Dlimi S, El kaaouachi A, Limouny L, et al. A crossover from Efros-Shklovskii hopping to activated transport in a GaAs two-dimensional hole system at low temperatures. J Semicond, 2021, 42, 052001 doi: 10.1088/1674-4926/42/5/052001[30] Street R A. Hydrogenated amorphous silicon. Cambridge University Press, 1991[31] Miller A, Abrahams E. Impurity conduction at low concentrations. Phys Rev, 1960, 120, 745 doi: 10.1103/PhysRev.120.745[32] Mott N F. Conduction in non-crystalline materials. Oxford: Clarendon Press, 1987[33] Mott N F, Davis E A. Electronic processes in non-crystalline materials. Oxford: Clarendon Press, 1971[34] van Keuls F W, Hu X L, Jiang H W, et al. Screening of the Coulomb interaction in two-dimensional variable-range hopping. Phys Rev B, 1997, 56, 1161 doi: 10.1103/PhysRevB.56.1161[35] Adkins C J. Conduction in granular metals-variable-range hopping in a Coulomb gap? J Phys: Condens Matter, 1989, 1, 1253 doi: 10.1088/0953-8984/1/7/009/meta[36] Penney T, von Molnár S, et al. Low-temperature transport properties of Cd0.91Mn0.09Te: In and evidence for a magnetic hard gap in the density of states. Phys Rev Lett, 1992, 69, 1800 doi: 10.1103/PhysRevLett.69.1800[37] Evers F, Mirlin A D. Anderson transitions. Rev Modern Phys, 2008, 80, 63 doi: 10.1103/RevModPhys.80.1355[38] Egli D, Fröhlich J, Ott H R. Anderson localization triggered by spin disorder – with an application to Eu xCa1– xB6. J Statist Phys, 2011, 143, 970 doi: 10.1007/s10955-011-0216-9[39] Wojtowicz T, Mycielski A. Magnetic field induced nonmetal-metal transition in the open-gap Hg1– xMn xTe. Phys B+C, 1983, 117, 476 doi: 10.1016/0378-4363(83)90563-6[40] Wojtowicz T, Gawron T R, Robert J L, et al. Hopping conductions studies of p-Hg1− xMn xTe in high magnetic fields: Unusual anisotropy of resistivity. J Cryst Growth, 1985, 72, 385 doi: 10.1016/0022-0248(85)90178-2[41] Mycielski J. Shallow acceptors in DMS: Splitting, boil-off, giant negative magnetoresistance. Semiconductors and Semimetals, 1988, 25, 311[42] Moca C P, Sheu B L, Samarth N, et al. Scaling theory of magnetoresistance and carrier localization in Ga1– xMn xAs. Phys Rev Lett, 2009, 102, 137203 doi: 10.1103/PhysRevLett.102.137203 -
Supplements
 2022-112502.pdf
2022-112502.pdf

-
Proportional views





 DownLoad:
DownLoad: