| Citation: |
Jia Chen, Jiancong Li, Yi Li, Xiangshui Miao. Multiply accumulate operations in memristor crossbar arrays for analog computing[J]. Journal of Semiconductors, 2021, 42(1): 013104. doi: 10.1088/1674-4926/42/1/013104
****
J Chen, J C Li, Y Li, X S Miao, Multiply accumulate operations in memristor crossbar arrays for analog computing[J]. J. Semicond., 2021, 42(1): 013104. doi: 10.1088/1674-4926/42/1/013104.
|
Multiply accumulate operations in memristor crossbar arrays for analog computing
DOI: 10.1088/1674-4926/42/1/013104
More Information
-
Abstract
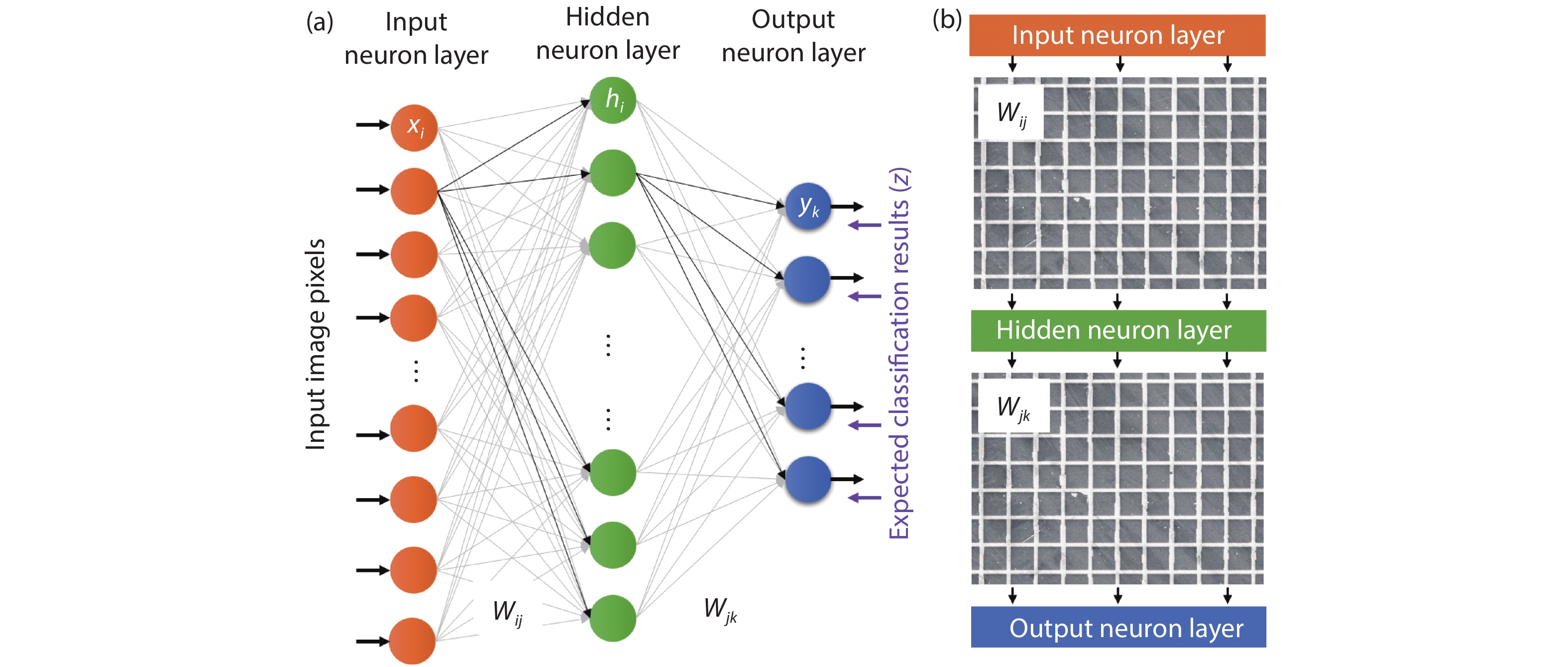
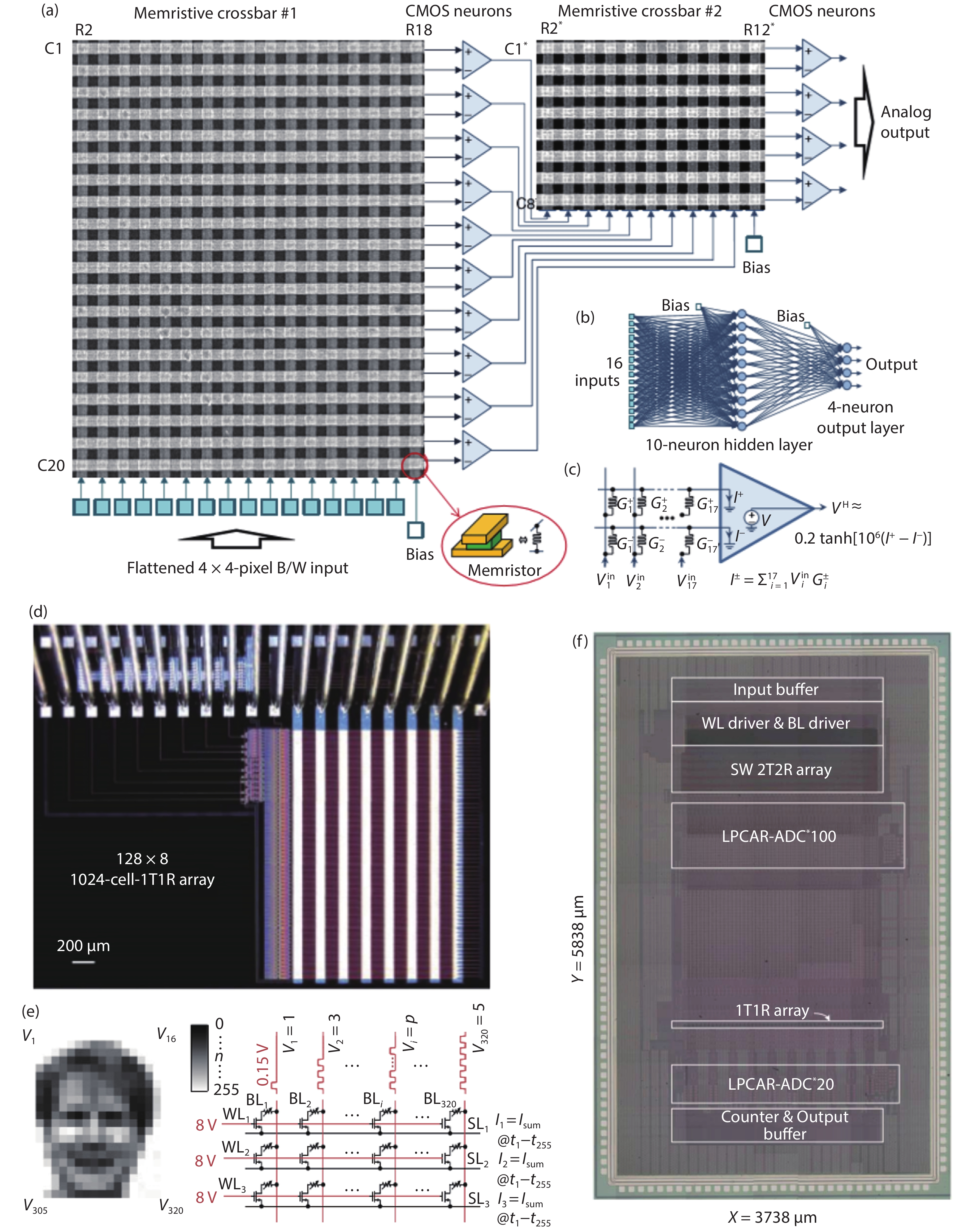
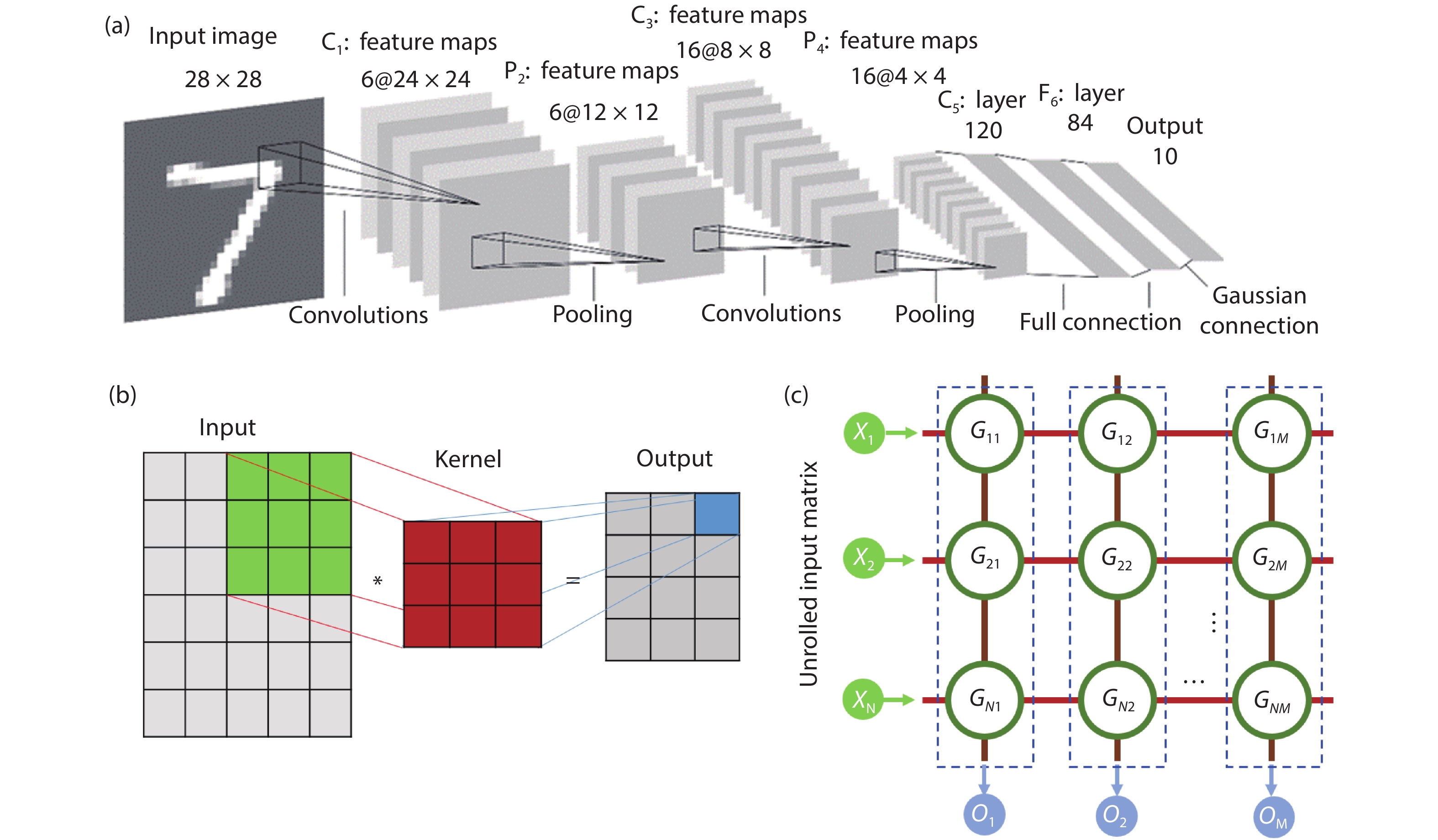
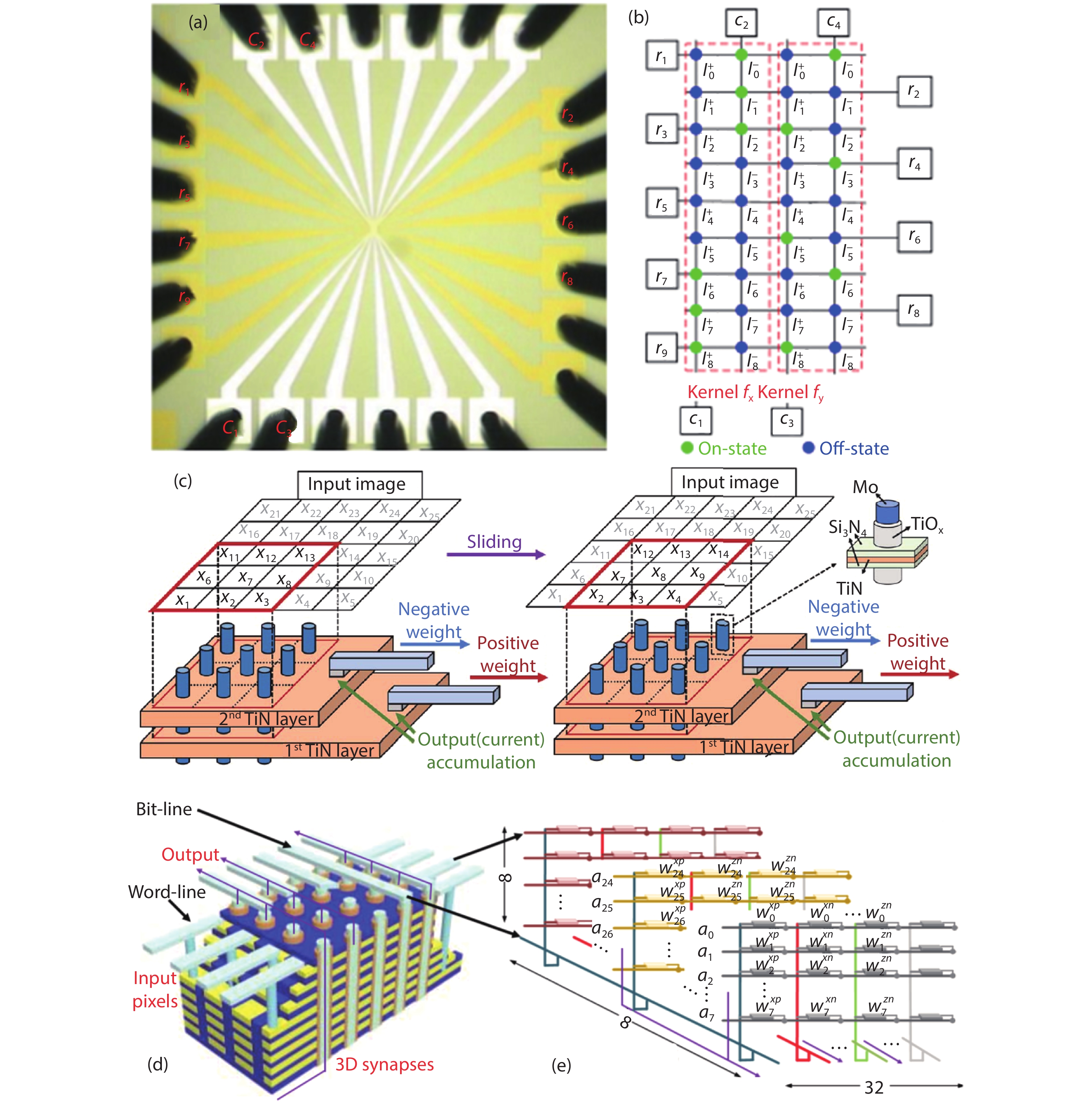
Memristors are now becoming a prominent candidate to serve as the building blocks of non-von Neumann in-memory computing architectures. By mapping analog numerical matrices into memristor crossbar arrays, efficient multiply accumulate operations can be performed in a massively parallel fashion using the physics mechanisms of Ohm’s law and Kirchhoff’s law. In this brief review, we present the recent progress in two niche applications: neural network accelerators and numerical computing units, mainly focusing on the advances in hardware demonstrations. The former one is regarded as soft computing since it can tolerant some degree of the device and array imperfections. The acceleration of multiple layer perceptrons, convolutional neural networks, generative adversarial networks, and long short-term memory neural networks are described. The latter one is hard computing because the solving of numerical problems requires high-precision devices. Several breakthroughs in memristive equation solvers with improved computation accuracies are highlighted. Besides, other nonvolatile devices with the capability of analog computing are also briefly introduced. Finally, we conclude the review with discussions on the challenges and opportunities for future research toward realizing memristive analog computing machines. -
References
[1] Backus J. Can programming be liberated from the von Neumann style. Commun ACM, 1978, 21, 613 doi: 10.1145/359576.359579[2] Moore G. Moore’s law. Electron Magaz, 1965, 38, 114[3] Schaller R R. Moore's law: Past, present and future. IEEE Spectr, 1997, 34, 52 doi: 10.1109/6.591665[4] Mack C A. Fifty years of Moore's law. IEEE Trans Semicond Manufact, 2011, 24, 202 doi: 10.1109/TSM.2010.2096437[5] Waldrop M M. The chips are down for Moore's law. Nature, 2016, 530, 144 doi: 10.1038/530144a[6] Wulf W A, McKee S A. Hitting the memory wall. SIGARCH Comput Archit News, 1995, 23, 20[7] Ielmini D, Wong H S P. In-memory computing with resistive switching devices. Nat Electron, 2018, 1, 333 doi: 10.1038/s41928-018-0092-2[8] le Gallo M, Sebastian A, Mathis R, et al. Mixed-precision in-memory computing. Nat Electron, 2018, 1, 246 doi: 10.1038/s41928-018-0054-8[9] Kendall J D, Kumar S. The building blocks of a brain-inspired computer. Appl Phys Rev, 2020, 7, 011305 doi: 10.1063/1.5129306[10] Sebastian A, Le Gallo M, Khaddam-Aljameh R, et al. Memory devices and applications for in-memory computing. Nat Nanotechnol, 2020, 15, 529 doi: 10.1038/s41565-020-0655-z[11] Lee S H, Zhu X J, Lu W D. Nanoscale resistive switching devices for memory and computing applications. Nano Res, 2020, 13, 1228 doi: 10.1007/s12274-020-2616-0[12] Upadhyay N K, Jiang H, Wang Z R, et al. Emerging memory devices for neuromorphic computing. Adv Mater Technol, 2019, 4, 1800589 doi: 10.1002/admt.201800589[13] Islam R, Li H T, Chen P Y, et al. Device and materials requirements for neuromorphic computing. J Phys D, 2019, 52, 113001 doi: 10.1088/1361-6463/aaf784[14] Krestinskaya O, James A P, Chua L O. Neuromemristive circuits for edge computing: A review. IEEE Trans Neural Netw Learn Syst, 2020, 31, 4 doi: 10.1109/TNNLS.2019.2899262[15] Rajendran B, Sebastian A, Schmuker M, et al. Low-power neuromorphic hardware for signal processing applications: A review of architectural and system-level design approaches. IEEE Signal Process Mag, 2019, 36, 97 doi: 10.1109/MSP.2019.2933719[16] Singh G, Chelini L, Corda S, et al. A review of near-memory computing architectures: Opportunities and challenges. 2018 21st Euromicro Conference on Digital System Design (DSD), 2018, 608[17] Singh G, Chelini L, Corda S, et al. Near-memory computing: Past, present, and future. Microprocess Microsyst, 2019, 71, 102868 doi: 10.1016/j.micpro.2019.102868[18] Merolla P A, Arthur J V, Alvarez-Icaza R, et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science, 2014, 345, 668 doi: 10.1126/science.1254642[19] Chen Y J, Luo T, Liu S L, et al. DaDianNao: A machine-learning supercomputer. 2014 47th Annual IEEE/ACM International Symposium on Microarchitecture, 2014, 609[20] Davies M, Srinivasa N, Lin T H, et al. Loihi: A neuromorphic manycore processor with on-chip learning. IEEE Micro, 2018, 38, 82 doi: 10.1109/MM.2018.112130359[21] Pei J, Deng L, Song S, et al. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature, 2019, 572, 106 doi: 10.1038/s41586-019-1424-8[22] Chua L. Memristor – The missing circuit element. IEEE Trans Circuit Theory, 1971, 18, 507 doi: 10.1109/TCT.1971.1083337[23] Wong H S P, Raoux S, Kim S, et al. Phase change memory. Proc IEEE, 2010, 98, 2201 doi: 10.1109/JPROC.2010.2070050[24] Paz de Araujo C A, McMillan L D, Melnick B M, et al. Ferroelectric memories. Ferroelectrics, 1990, 104, 241 doi: 10.1080/00150199008223827[25] Apalkov D, Khvalkovskiy A, Watts S, et al. Spin-transfer torque magnetic random access memory (STT-MRAM). J Emerg Technol Comput Syst, 2013, 9, 1 doi: 10.1145/2463585.2463589[26] Wang Z R, Wu H Q, Burr G W, et al. Resistive switching materials for information processing. Nat Rev Mater, 2020, 5, 173 doi: 10.1038/s41578-019-0159-3[27] Lanza M, Wong H S P, Pop E, et al. Recommended methods to study resistive switching devices. Adv Electron Mater, 2019, 5, 1800143 doi: 10.1002/aelm.201800143[28] Waser R, Dittmann R, Staikov G, et al. Redox-based resistive switching memories–nanoionic mechanisms, prospects, and challenges. Adv Mater, 2009, 21, 2632 doi: 10.1002/adma.200900375[29] Pi S, Li C, Jiang H, et al. Memristor crossbar arrays with 6-nm half-pitch and 2-nm critical dimension. Nat Nanotechnol, 2019, 14, 35 doi: 10.1038/s41565-018-0302-0[30] Choi B J, Torrezan A C, Strachan J P, et al. High-speed and low-energy nitride memristors. Adv Funct Mater, 2016, 26, 5290 doi: 10.1002/adfm.201600680[31] Lin P, Li C, Wang Z, et al. Three-dimensional memristor circuits as complex neural networks. Nat Electron, 2020, 3, 225 doi: 10.1038/s41928-020-0397-9[32] Jo S H, Chang T, Ebong I, et al. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett, 2010, 10, 1297 613 doi: 10.1021/nl904092h[33] Abdelgawad A, Bayoumi M. High speed and area-efficient multiply accumulate (MAC) unit for digital signal prossing applications. 2007 IEEE International Symposium on Circuits and Systems, 2007, 3199[34] Pawar R, Shriramwar D S S. Review on multiply-accumulate unit. Int J Eng Res Appl, 2017, 7, 09 doi: 10.9790/9622-0706040913[35] Tung C W, Huang S H. A high-performance multiply-accumulate unit by integrating additions and accumulations into partial product reduction process. IEEE Access, 2020, 8, 87367 doi: 10.1109/ACCESS.2020.2992286[36] Zhang H, He J R, Ko S B. Efficient posit multiply-accumulate unit generator for deep learning applications. 2019 IEEE International Symposium on Circuits and Systems (ISCAS), 2019, 1[37] Camus V, Mei L Y, Enz C, et al. Review and benchmarking of precision-scalable multiply-accumulate unit architectures for embedded neural-network processing. IEEE J Emerg Sel Topics Circuits Syst, 2019, 9, 697 doi: 10.1109/JETCAS.2019.2950386[38] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. Commun ACM, 2017, 60, 84 doi: 10.1145/3065386[39] Hu M, Strachan J P, Li Z Y, et al. Dot-product engine for neuromorphic computing: Programming 1T1M crossbar to accelerate matrix-vector multiplication. 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), 2016, 1[40] Hu M, Graves C E, Li C, et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv Mater, 2018, 30, 1705914 doi: 10.1002/adma.201705914[41] Li C, Hu M, Li Y, et al. Analogue signal and image processing with large memristor crossbars. Nat Electron, 2018, 1, 52 doi: 10.1038/s41928-017-0002-z[42] Liu M Y, Xia L X, Wang Y, et al. Algorithmic fault detection for RRAM-based matrix operations. ACM Trans Des Autom Electron Syst, 2020, 25, 1 doi: 10.1145/3386360[43] Wang M Q, Deng N, Wu H Q, et al. Theory study and implementation of configurable ECC on RRAM memory. 2015 15th Non-Volatile Memory Technology Symposium (NVMTS), 2015, 1[44] Niu D M, Yang X, Yuan X. Low power memristor-based ReRAM design with Error Correcting Code. 17th Asia and South Pacific Design Automation Conference, 2012, 79[45] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Networks, 1989, 2, 359 doi: 10.1016/0893-6080(89)90020-8[46] LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521, 436 doi: 10.1038/nature14539[47] Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, 105[48] Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput, 1997, 9, 1735 doi: 10.1162/neco.1997.9.8.1735[49] Chen Y H, Krishna T, Emer J S, et al. Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J Solid-State Circuits, 2017, 52, 127 doi: 10.1109/JSSC.2016.2616357[50] DeepBench, Baidu. https://github.com/baidu-research/DeepBench[51] Adolf R, Rama S, Reagen B, et al. Fathom: reference workloads for modern deep learning methods. 2016 IEEE International Symposium on Workload Characterization (IISWC), 2016, 1[52] Huang X D, Li Y, Li H Y, et al. Forming-free, fast, uniform, and high endurance resistive switching from cryogenic to high temperatures in W/AlOx/Al2O3/Pt bilayer memristor. IEEE Electron Device Lett, 2020, 41, 549 doi: 10.1109/LED.2020.2977397[53] Choi S, Tan S H, Li Z F, et al. SiGe epitaxial memory for neuromorphic computing with reproducible high performance based on engineered dislocations. Nat Mater, 2018, 17, 335 doi: 10.1038/s41563-017-0001-5[54] Li Y B, Wang Z R, Midya R, et al. Review of memristor devices in neuromorphic computing: Materials sciences and device challenges. J Phys D, 2018, 51, 503002 doi: 10.1088/1361-6463/aade3f[55] Kim S G, Han J S, Kim H, et al. Recent advances in memristive materials for artificial synapses. Adv Mater Technol, 2018, 3, 1800457 doi: 10.1002/admt.201800457[56] Xia Q F, Yang J J. Memristive crossbar arrays for brain-inspired computing. Nat Mater, 2019, 18, 309 doi: 10.1038/s41563-019-0291-x[57] Zhu J D, Zhang T, Yang Y C, et al. A comprehensive review on emerging artificial neuromorphic devices. Appl Phys Rev, 2020, 7, 011312 doi: 10.1063/1.5118217[58] Cristiano G, Giordano M, Ambrogio S, et al. Perspective on training fully connected networks with resistive memories: Device requirements for multiple conductances of varying significance. J Appl Phys, 2018, 124, 151901 doi: 10.1063/1.5042462[59] Agarwal S, Plimpton S J, Hughart D R, et al. Resistive memory device requirements for a neural algorithm accelerator. 2016 International Joint Conference on Neural Networks (IJCNN), 2016, 929[60] Tsai H, Ambrogio S, Narayanan P, et al. Recent progress in analog memory-based accelerators for deep learning. J Phys D, 2018, 51, 283001 doi: 10.1088/1361-6463/aac8a5[61] Chen P Y, Peng X C, Yu S M. NeuroSim: A circuit-level macro model for benchmarking neuro-inspired architectures in online learning. IEEE Trans Comput-Aided Des Integr Circuits Syst, 2018, 37, 3067 doi: 10.1109/TCAD.2018.2789723[62] Yan B N, Li B, Qiao X M, et al. Resistive memory-based in-memory computing: From device and large-scale integration system perspectives. Adv Intell Syst, 2019, 1, 1900068 doi: 10.1002/aisy.201900068[63] Chen J, Lin C Y, Li Y, et al. LiSiOx-based analog memristive synapse for neuromorphic computing. IEEE Electron Device Lett, 2019, 40, 542 doi: 10.1109/LED.2019.2898443[64] Oh S, Kim T, Kwak M, et al. HfZrOx-based ferroelectric synapse device with 32 levels of conductance states for neuromorphic applications. IEEE Electron Device Lett, 2017, 38, 732 doi: 10.1109/LED.2017.2698083[65] Park J, Kwak M, Moon K, et al. TiOx-based RRAM synapse with 64-levels of conductance and symmetric conductance change by adopting a hybrid pulse scheme for neuromorphic computing. IEEE Electron Device Lett, 2016, 37, 1559 doi: 10.1109/LED.2016.2622716[66] Cheng Y, Wang C, Chen H B, et al. A large-scale in-memory computing for deep neural network with trained quantization. Integration, 2019, 69, 345 doi: 10.1016/j.vlsi.2019.08.004[67] Yang Q, Li H, Wu Q. A quantized training method to enhance accuracy of ReRAM-based neuromorphic systems. 2018 IEEE International Symposium on Circuits and Systems (ISCAS), 2018, 1[68] Yu S M, Li Z W, Chen P Y, et al. Binary neural network with 16 Mb RRAM macro chip for classification and online training. 2016 IEEE International Electron Devices Meeting (IEDM), 2016, 16.2.1[69] Bayat F M, Prezioso M, Chakrabarti B, et al. Implementation of multilayer perceptron network with highly uniform passive memristive crossbar circuits. Nat Commun, 2018, 9, 2331 doi: 10.1038/s41467-018-04482-4[70] Yao P, Wu H Q, Gao B, et al. Face classification using electronic synapses. Nat Commun, 2017, 8, 15199 doi: 10.1038/ncomms15199[71] Liu Q, Gao B, Yao P, et al. A fully integrated analog ReRAM based 78.4TOPS/W compute-in-memory chip with fully parallel MAC computing. 2020 IEEE International Solid- State Circuits Conference (ISSCC), 2020, 500[72] Li C, Belkin D, Li Y N, et al. Efficient and self-adaptive in situ learning in multilayer memristor neural networks. Nat Commun, 2018, 9, 2385 doi: 10.1038/s41467-018-04484-2[73] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv: 1409.1556, 2014[74] Cai F, Correll J M, Lee S H, et al. A fully integrated reprogrammable memristor–CMOS system for efficient multiply–accumulate operations. Nat Electron, 2019, 2, 290 doi: 10.1038/s41928-019-0270-x[75] LeCun Y. LeNet-5, convolutional neural networks. URL: http://yann.lecun.com/exdb/lenet, 2015, 20, 14[76] He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 770[77] Deguchi Y, Maeda K, Suzuki S, et al. Error-reduction controller techniques of TaOx-based ReRAM for deep neural networks to extend data-retention lifetime by over 1700x. 2018 IEEE Int Mem Work IMW, 2018, 1[78] Chen J, Pan W Q, Li Y, et al. High-precision symmetric weight update of memristor by gate voltage ramping method for convolutional neural network accelerator. IEEE Electron Device Lett, 2020, 41, 353 doi: 10.1109/LED.2020.2968388[79] Wu K C, Wang X P, Li M. Better performance of memristive convolutional neural network due to stochastic memristors. International Symposium on Neural Networks, 2019, 39 doi: 10.1007/978-3-030-22796-8_5[80] Xiang Y C, Huang P, Zhao Y D, et al. Impacts of state instability and retention failure of filamentary analog RRAM on the performance of deep neural network. IEEE Trans Electron Devices, 2019, 66, 4517 doi: 10.1109/TED.2019.2931135[81] Pan W Q, Chen J, Kuang R, et al. Strategies to improve the accuracy of memristor-based convolutional neural networks. IEEE Trans Electron Devices, 2020, 67, 895 doi: 10.1109/TED.2019.2963323[82] Gokmen T, Onen M, Haensch W. Training deep convolutional neural networks with resistive cross-point devices. Front Neurosci, 2017, 11, 538 doi: 10.3389/fnins.2017.00538[83] Lin Y H, Wang C H, Lee M H, et al. Performance impacts of analog ReRAM non-ideality on neuromorphic computing. IEEE Trans Electron Devices, 2019, 66, 1289 doi: 10.1109/TED.2019.2894273[84] Gao L G, Chen P Y, Yu S M. Demonstration of convolution kernel operation on resistive cross-point array. IEEE Electron Device Lett, 2016, 37, 870 doi: 10.1109/LED.2016.2573140[85] Kwak M, Park J, Woo J, et al. Implementation of convolutional kernel function using 3-D TiOx resistive switching devices for image processing. IEEE Trans Electron Devices, 2018, 65, 4716 doi: 10.1109/TED.2018.2862139[86] Huo Q, Song R J, Lei D Y, et al. Demonstration of 3D convolution kernel function based on 8-layer 3D vertical resistive random access memory. IEEE Electron Device Lett, 2020, 41, 497 doi: 10.1109/LED.2020.2970536[87] Yao P, Wu H Q, Gao B, et al. Fully hardware-implemented memristor convolutional neural network. Nature, 2020, 577, 641 doi: 10.1038/s41586-020-1942-4[88] Chen W H, Dou C, Li K X, et al. CMOS-integrated memristive non-volatile computing-in-memory for AI edge processors. Nat Electron, 2019, 2, 420 doi: 10.1038/s41928-019-0288-0[89] Xue C X, Chang T W, Chang T C, et al. Embedded 1-Mb ReRAM-based computing-in-memory macro with multibit input and weight for CNN-based AI edge processors. IEEE J Solid-State Circuits, 2020, 55, 203 doi: 10.1109/JSSC.2019.2951363[90] Chen F, Song L H, Chen Y R. ReGAN: A pipelined ReRAM-based accelerator for generative adversarial networks. 2018 23rd Asia and South Pacific Design Automation Conference (ASP-DAC), 2018, 178.[91] Lin Y D, Wu H Q, Gao B, et al. Demonstration of generative adversarial network by intrinsic random noises of analog RRAM devices. 2018 IEEE International Electron Devices Meeting (IEDM), 2018, 3.4.1[92] Li C, Wang Z R, Rao M Y, et al. Long short-term memory networks in memristor crossbar arrays. Nat Mach Intell, 2019, 1, 49 doi: 10.1038/s42256-018-0001-4[93] Tsai H, Ambrogio S, Mackin C, et al. Inference of Long-Short Term Memory networks at software-equivalent accuracy using 2.5M analog phase change memory devices. 2019 Symposium on VLSI Technology, 2019[94] Smagulova K, Krestinskaya O, James A P. A memristor-based long short term memory circuit. Analog Integr Circ Sig Process, 2018, 95, 467 doi: 10.1007/s10470-018-1180-y[95] Wen S P, Wei H Q, Yang Y, et al. Memristive LSTM network for sentiment analysis. IEEE Trans Syst Man Cybern: Syst, 2019, 1 doi: 10.1109/TSMC.2019.2906098[96] Smagulova K, James A P. A survey on LSTM memristive neural network architectures and applications. Eur Phys J Spec Top, 2019, 228, 2313 doi: 10.1140/epjst/e2019-900046-x[97] Yin S H, Sun X Y, Yu S M, et al. A parallel RRAM synaptic array architecture for energy-efficient recurrent neural networks. 2018 IEEE International Workshop on Signal Processing Systems (SiPS), 2018, 13[98] Zidan M A, Jeong Y, Lee J, et al. A general memristor-based partial differential equation solver. Nat Electron, 2018, 1, 411 doi: 10.1038/s41928-018-0100-6[99] Jouppi N P, Young C, Patil N, et al. In-datacenter performance analysis of a tensor processing unit. Proceedings of the 44th Annual International Symposium on Computer Architecture, 2017[100] Sun Z, Pedretti G, Ambrosi E, et al. Solving matrix equations in one step with cross-point resistive arrays. PNAS, 2019, 116, 4123 doi: 10.1073/pnas.1815682116[101] Sun Z, Ambrosi E, Pedretti G, et al. In-memory PageRank accelerator with a cross-point array of resistive memories. IEEE Trans Electron Devices, 2020, 67, 1466 doi: 10.1109/TED.2020.2966908[102] Sun Z, Pedretti G, Ielmini D. Fast solution of linear systems with analog resistive switching memory (RRAM). 2019 IEEE International Conference on Rebooting Computing (ICRC), 2019, 1[103] Sun Z, Pedretti G, Mannocci P, et al. Time complexity of in-memory solution of linear systems. IEEE Trans Electron Devices, 2020, 67, 2945 doi: 10.1109/TED.2020.2992435[104] Sun Z, Pedretti G, Ambrosi E, et al. In-memory eigenvector computation in time O (1). Adv Intell Syst, 2020, 2, 2000042 doi: 10.1002/aisy.202000042[105] Feng Y, Zhan X P, Chen J Z. Flash memory based computing-in-memory to solve time-dependent partial differential equations. 2020 IEEE Silicon Nanoelectronics Workshop (SNW), 2020, 27[106] Zhou H L, Zhao Y H, Xu G X, et al. Chip-scale optical matrix computation for PageRank algorithm. IEEE J Sel Top Quantum Electron, 2020, 26, 1 doi: 10.1109/JSTQE.2019.2943347[107] Milo V, Malavena G, Compagnoni C M, et al. Memristive and CMOS devices for neuromorphic computing. Materials, 2020, 13, 166 doi: 10.3390/ma13010166[108] Ambrogio S, Narayanan P, Tsai H, et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature, 2018, 558, 60 doi: 10.1038/s41586-018-0180-5[109] Jerry M, Chen P Y, Zhang J C, et al. Ferroelectric FET analog synapse for acceleration of deep neural network training. 2017 IEEE International Electron Devices Meeting (IEDM), 2017, 6.2.1[110] Guo X, Bayat F M, Bavandpour M, et al. Fast, energy-efficient, robust, and reproducible mixed-signal neuromorphic classifier based on embedded NOR flash memory technology. 2017 IEEE International Electron Devices Meeting (IEDM), 2017, 6.5.1[111] Bichler O, Suri M N, Querlioz D, et al. Visual pattern extraction using energy-efficient “2-PCM synapse” neuromorphic architecture. IEEE Trans Electron Devices, 2012, 59, 2206 doi: 10.1109/TED.2012.2197951[112] Suri M N, Bichler O, Querlioz D, et al. Phase change memory as synapse for ultra-dense neuromorphic systems: Application to complex visual pattern extraction. 2011 International Electron Devices Meeting, 2011, 4.4.1[113] Burr G W, Shelby R M, Sidler S, et al. Experimental demonstration and tolerancing of a large-scale neural network (165 000 synapses) using phase-change memory as the synaptic weight element. IEEE Trans Electron Devices, 2015, 62, 3498 doi: 10.1109/TED.2015.2439635[114] Oh S, Huang Z S, Shi Y H, et al. The impact of resistance drift of phase change memory (PCM) synaptic devices on artificial neural network performance. IEEE Electron Device Lett, 2019, 40, 1325 doi: 10.1109/LED.2019.2925832[115] Spoon K, Ambrogio S, Narayanan P, et al. Accelerating deep neural networks with analog memory devices. 2020 IEEE International Memory Workshop (IMW), 2020, 1[116] Chen L, Wang T Y, Dai Y W, et al. Ultra-low power Hf0.5Zr0.5O2 based ferroelectric tunnel junction synapses for hardware neural network applications. Nanoscale, 2018, 10, 15826 doi: 10.1039/C8NR04734K[117] Boyn S, Grollier J, Lecerf G, et al. Learning through ferroelectric domain dynamics in solid-state synapses. Nat Commun, 2017, 8, 14736 doi: 10.1038/ncomms14736[118] Hu V P H, Lin H H, Zheng Z A, et al. Split-gate FeFET (SG-FeFET) with dynamic memory window modulation for non-volatile memory and neuromorphic applications. 2019 Symposium on VLSI Technology, 2019[119] Sun X Y, Wang P N, Ni K, et al. Exploiting hybrid precision for training and inference: A 2T-1FeFET based analog synaptic weight cell. 2018 IEEE International Electron Devices Meeting (IEDM), 2018, 3.1.1[120] Lee S T, Kim H, Bae J H, et al. High-density and highly-reliable binary neural networks using NAND flash memory cells as synaptic devices. 2019 IEEE International Electron Devices Meeting (IEDM), 2019, 38.4.1[121] Bavandpour M, Sahay S, Mahmoodi M R, et al. 3D-aCortex: An ultra-compact energy-efficient neurocomputing platform based on commercial 3D-NAND flash memories. arXiv: 1908.02472, 2019[122] Xiang Y C, Huang P, Han R Z, et al. Efficient and robust spike-driven deep convolutional neural networks based on NOR flash computing array. IEEE Trans Electron Devices, 2020, 67, 2329 doi: 10.1109/TED.2020.2987439[123] Xiang Y C, Huang P, Yang H Z, et al. Storage reliability of multi-bit flash oriented to deep neural network. 2019 IEEE International Electron Devices Meeting (IEDM), 2019, 38.2.1 -
Proportional views





 DownLoad:
DownLoad: