| Citation: |
Jian Li. Electronic structure of (InSb)m/(HgTe)n short period superlattices[J]. Journal of Semiconductors, 2014, 35(3): 032001. doi: 10.1088/1674-4926/35/3/032001
****
J Li. Electronic structure of (InSb)m/(HgTe)n short period superlattices[J]. J. Semicond., 2014, 35(3): 032001. doi: 10.1088/1674-4926/35/3/032001.
|
Electronic structure of (InSb)m/(HgTe)n short period superlattices
DOI: 10.1088/1674-4926/35/3/032001
More Information
-
Abstract
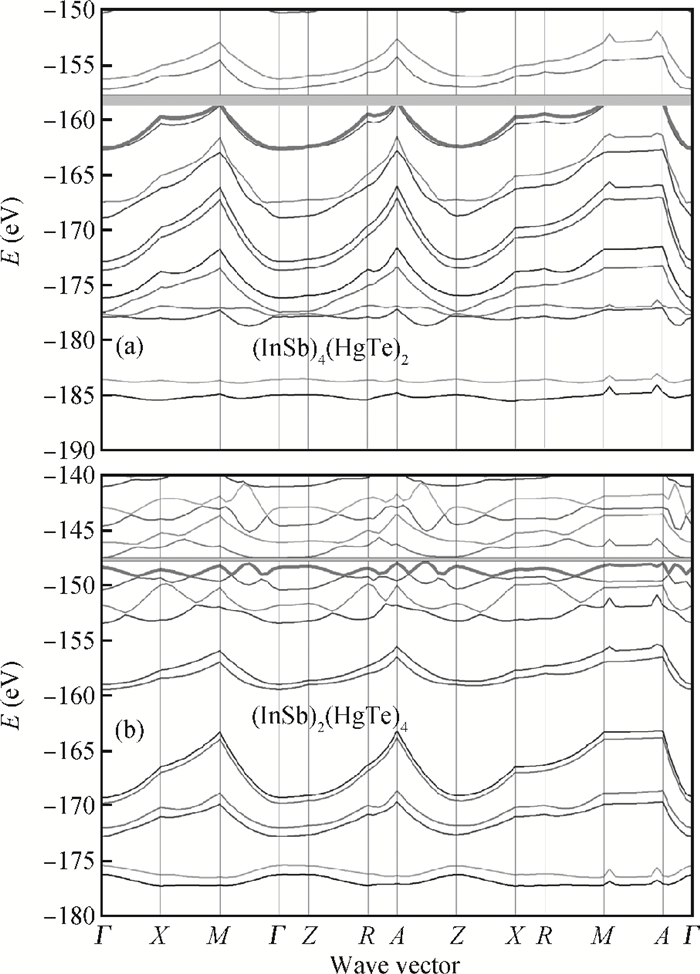
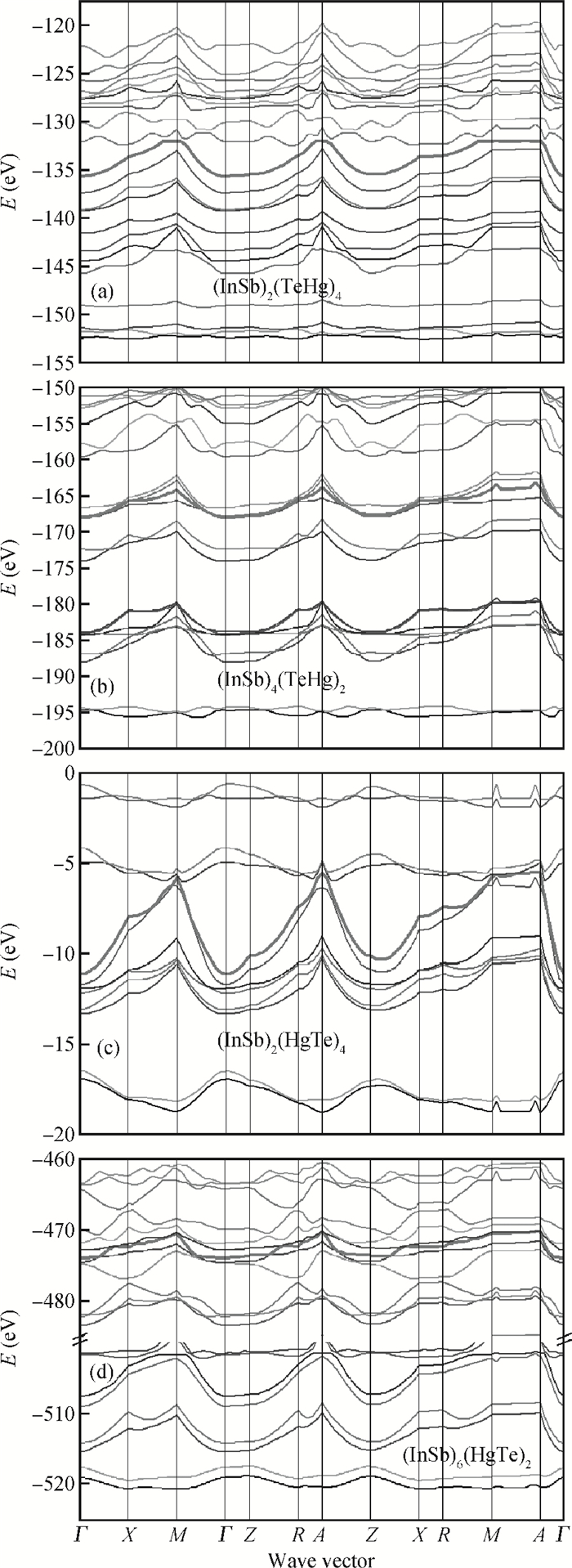
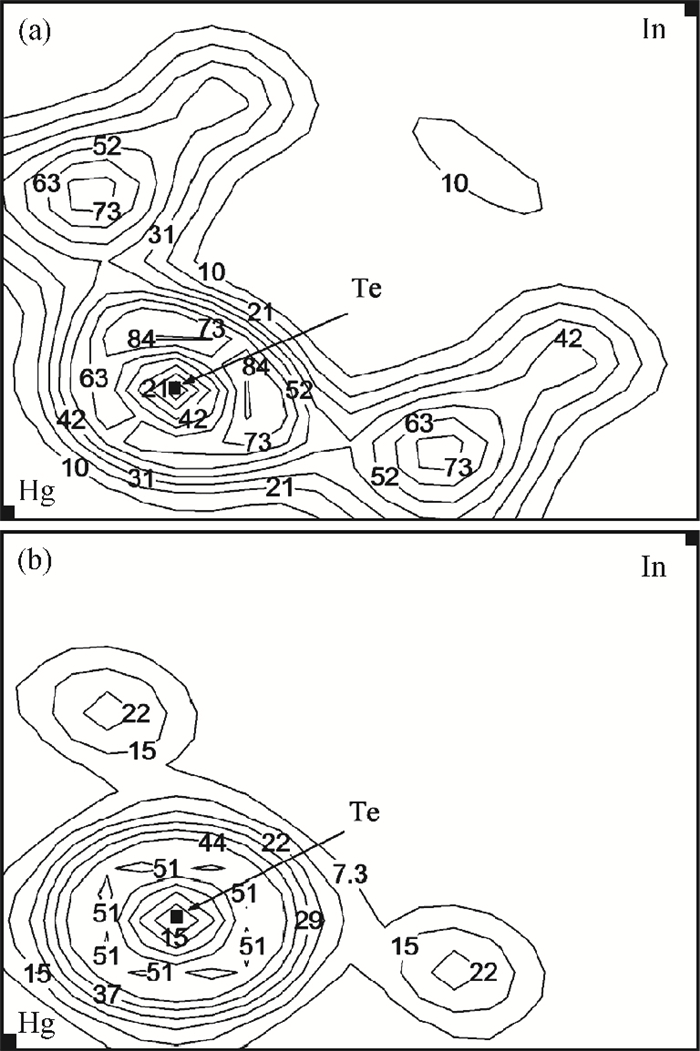
The electronic structure of (InSb)m/(HgTe)n short period superlattices grown along the (001) direction is studied theoretically using norm-conserving pseudo-potentials together with the local-density approximation for the exchange-correlation potential. The band structure depends on the value of m and n, the number of mono-layers and on the ordering of atoms at the InSb/HgTe interface in one unit cell. Our calculation indicates that the superlattice can be a semiconductor having a band gap between the occupied and unoccupied bands, or a metal with no band gap at the Fermi energy.According to the further calculation of total charge density between (InSb)m/(HgTe)n with different structures, a clearly different behavior happens when the structure changes from a system with a gap and a system without a gap. -
References
[1] Yan B, Zhang S. Topological materials. Rep Prog Phys, 2012, 75:096501 doi: 10.1088/0034-4885/75/9/096501[2] Knez I, Du R R. Quantum spin Hall effect in inverted InAs/GaSb quantum wells. Front Phys, 2012, 7(2):200 doi: 10.1007/s11467-011-0204-1[3] Gouider F, Vasilyew Y B, Konemann J, et al. THz detectors with HgTe and InSb quantum wells. 35th International Conference on Infrared, Millimeter, and Terahertz Waves, Rome, Italy, 2010 http://ieeexplore.ieee.org/abstract/document/5612596/[4] Christensen N. Dipole effects and band offsets at semiconductor interfaces. Phys Rev B, 1998, 37(9):4528 doi: 10.1103/PhysRevB.37.4528[5] Cohen M L, Bergstresser T K. Band structures and pseudopotential form factors for fourteen semiconductors of the diamond and zinc-blende structures. Phys Rev, 1966, 141(2):789 doi: 10.1103/PhysRev.141.789[6] Takeda T, Kübler J. Linear augmented plane wave method for self-consistent calculations. J Phys F:Met Phys, 1979, 9(4):661 doi: 10.1088/0305-4608/9/4/013[7] Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev, 1964, 136(3B):864 doi: 10.1103/PhysRev.136.B864[8] Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects. Phys Rev, 1965, 140(4A):1133 doi: 10.1103/PhysRev.140.A1133[9] Hamann D R, Schlüter M, Chiang C. Norm-consvering pseudopotentials. Phys Rev Lett, 1979, 43(20):1494 doi: 10.1103/PhysRevLett.43.1494[10] Pickett W E. Pseudopotential methonds in condensed matter applications. Comput Phys Rep, 1989, 9:115 doi: 10.1016/0167-7977(89)90002-6[11] Bachelet G B, Hamman D R, Schlüter M. Pseudopotentials that work:from H to Pu. Phys Rev B, 1982, 26(8):4199 doi: 10.1103/PhysRevB.26.4199[12] Ceperley D M, Alder B J. Ground state of the electron gas by a stochastic method. Phys Rev Lett, 1980, 45(7):566 doi: 10.1103/PhysRevLett.45.566[13] Perdew J P, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B, 1981, 23(10):5048 doi: 10.1103/PhysRevB.23.5048[14] Hartwigsen C, Goedecker S, Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys Rev B, 1998, 58(7):3641 doi: 10.1103/PhysRevB.58.3641[15] Walter J P, Cohen M L. Pseudopotential calculations of electronic charge densities in seven semiconductors. Phys Rev B, 1971, 4(6):1877 doi: 10.1103/PhysRevB.4.1877[16] Chadi D J, Cohe M L n. Electronic structure of Hg1-xCdxTe alloys and charge-density calculations using representative k points. Phys Rev B, 1973, 7(2):692 doi: 10.1103/PhysRevB.7.692 -
Proportional views





 DownLoad:
DownLoad: