| Citation: |
Bo Gu. High temperature magnetic semiconductors: narrow band gaps and two-dimensional systems[J]. Journal of Semiconductors, 2019, 40(8): 081504. doi: 10.1088/1674-4926/40/8/081504
****
B Gu, High temperature magnetic semiconductors: narrow band gaps and two-dimensional systems[J]. J. Semicond., 2019, 40(8): 081504. doi: 10.1088/1674-4926/40/8/081504.
|
High temperature magnetic semiconductors: narrow band gaps and two-dimensional systems
DOI: 10.1088/1674-4926/40/8/081504
More Information
-
Abstract
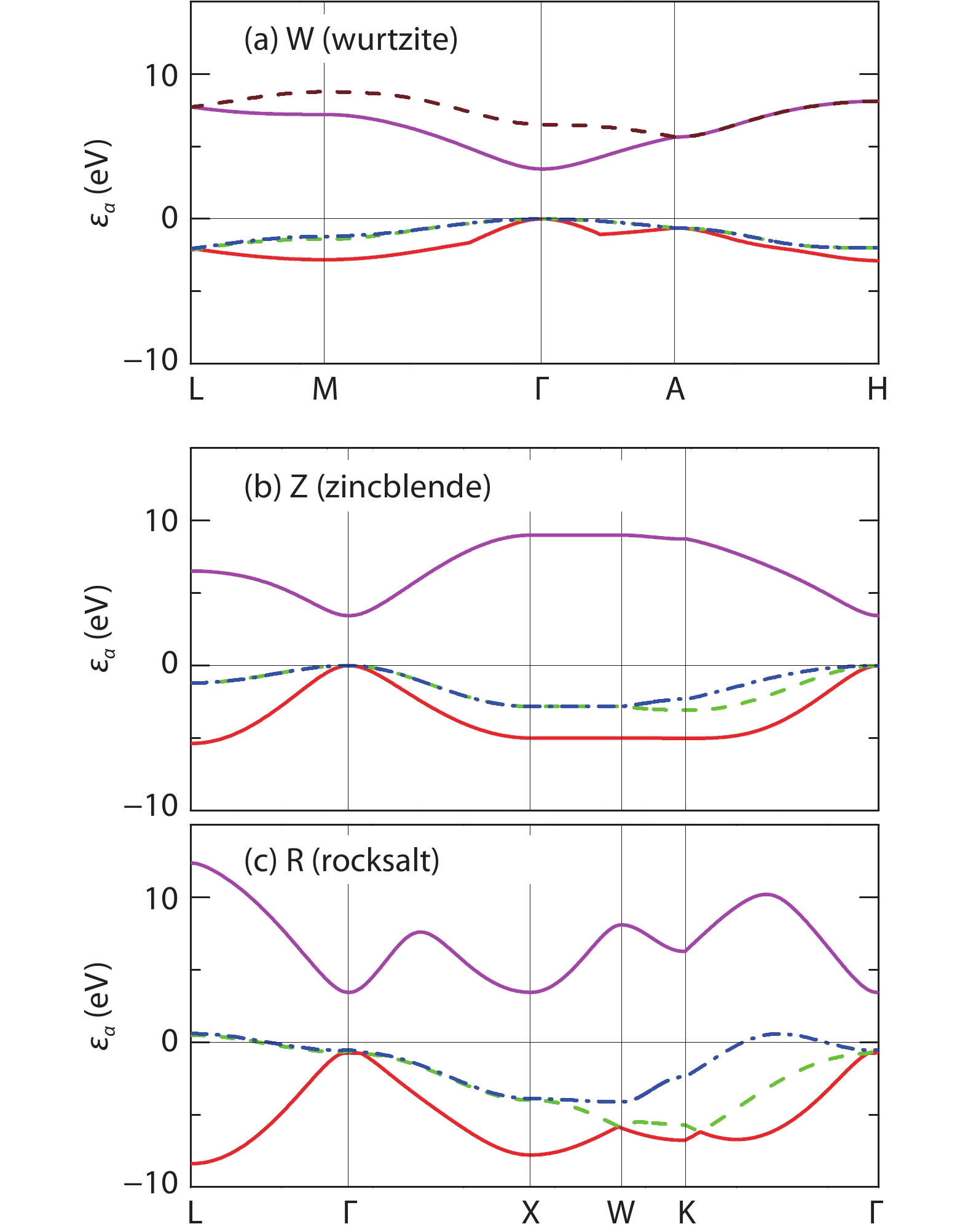
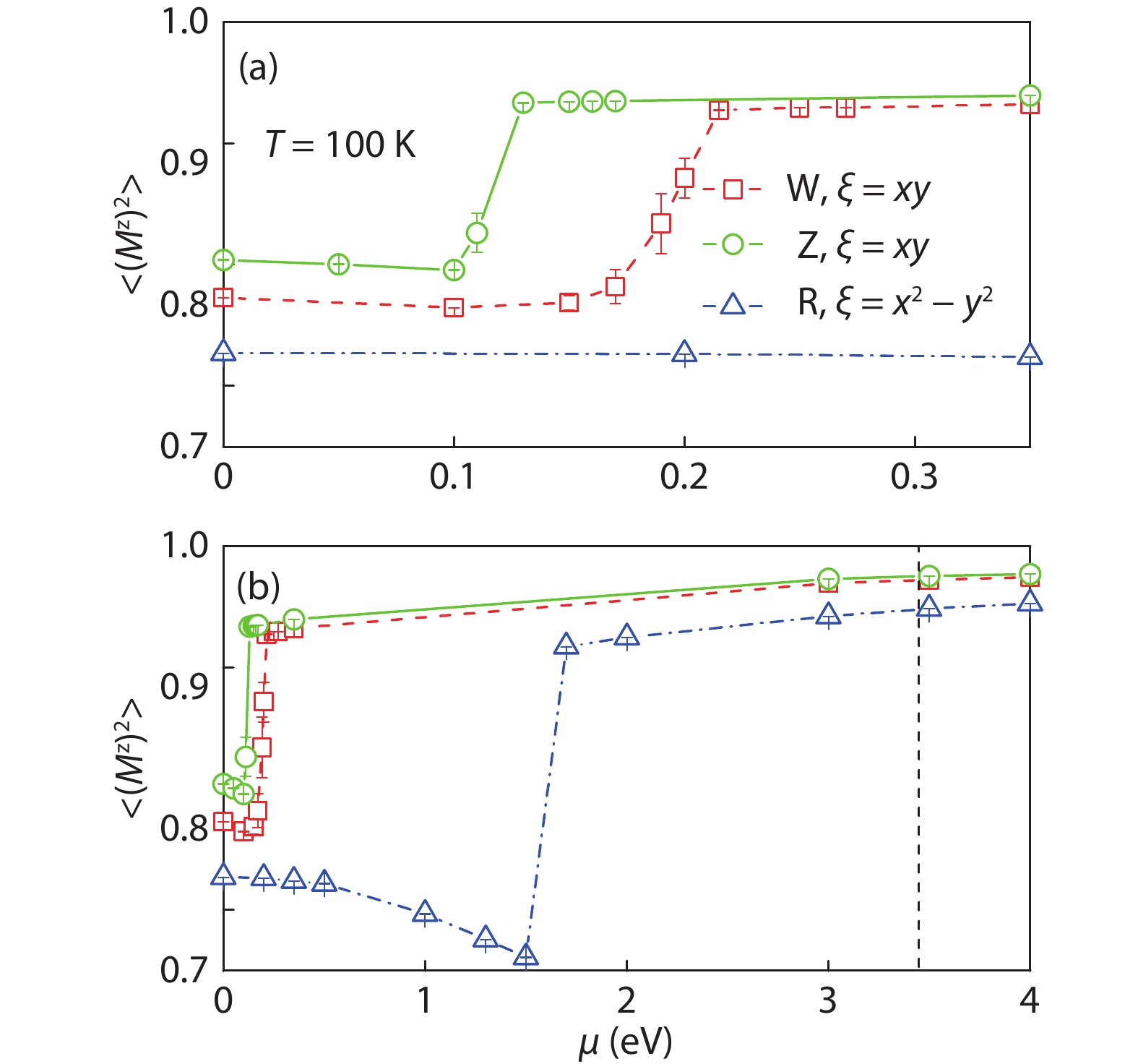
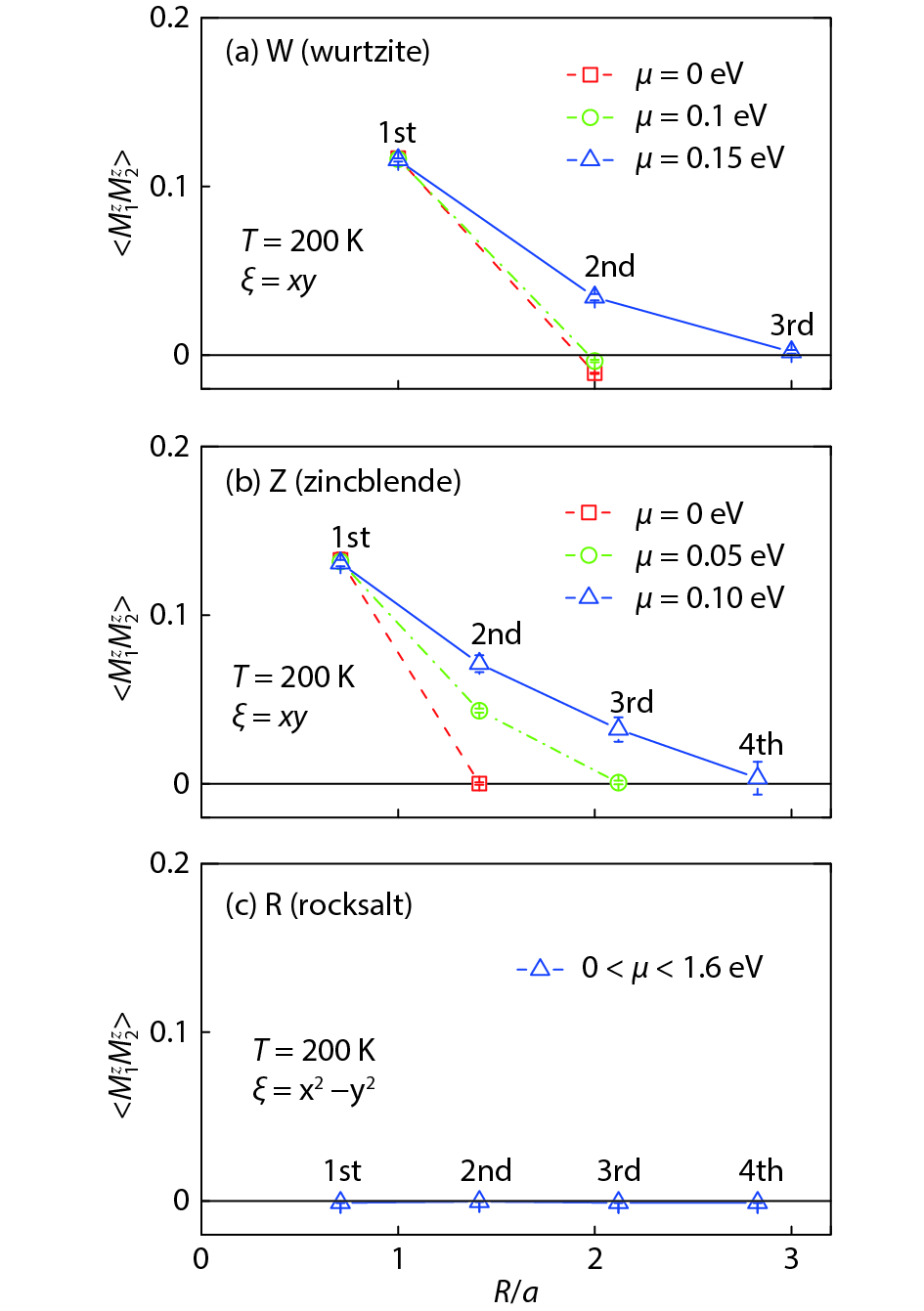
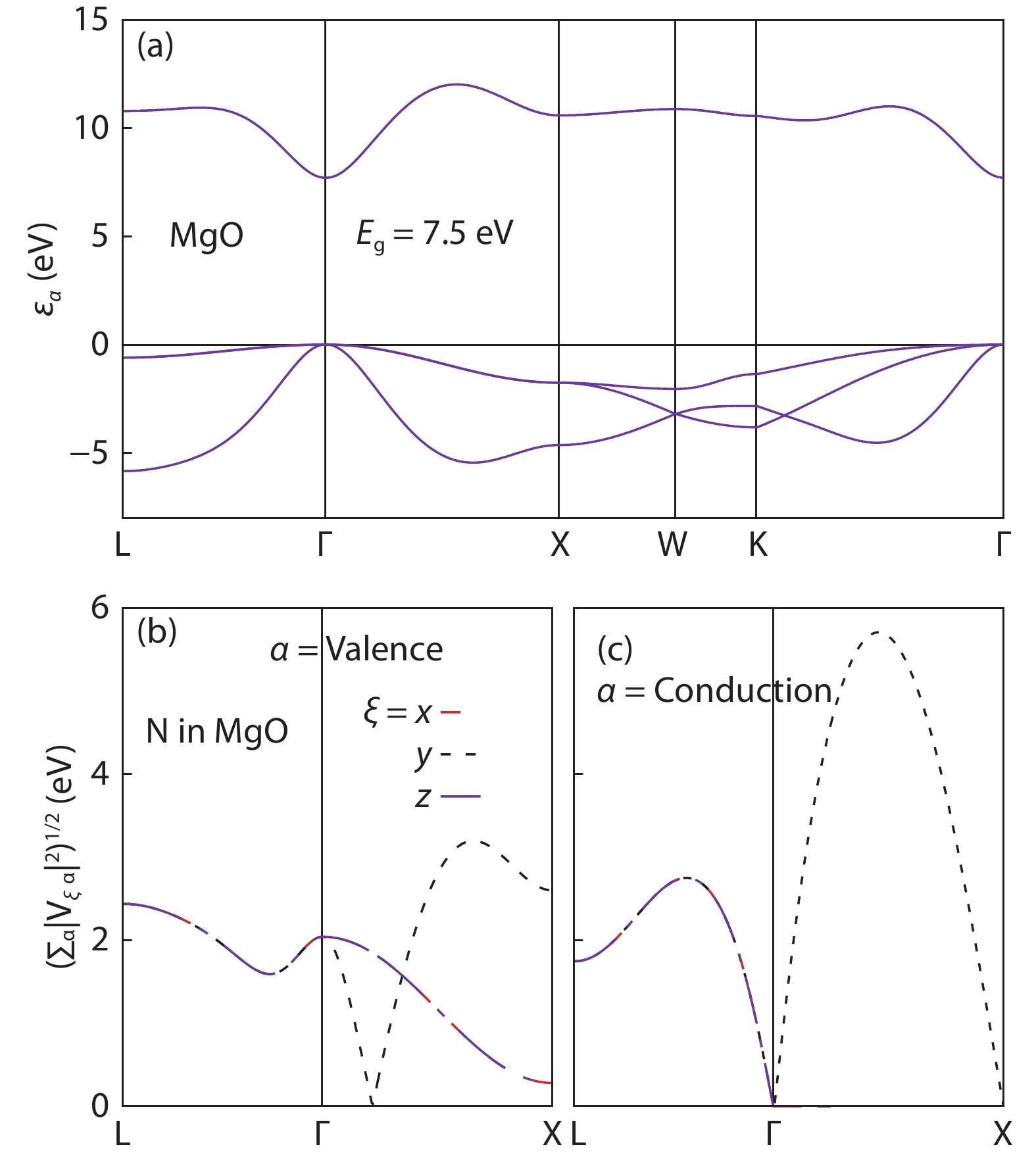
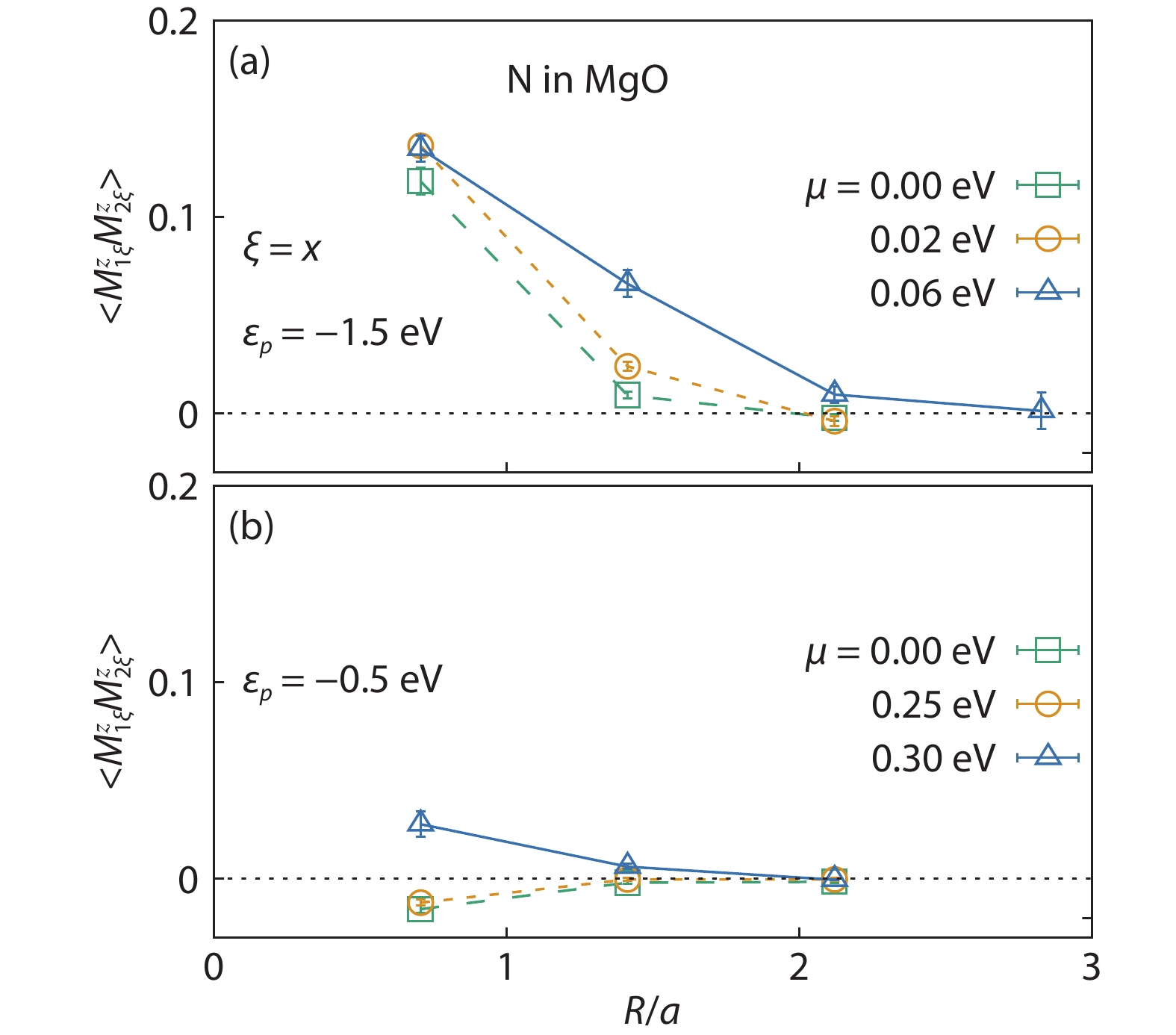
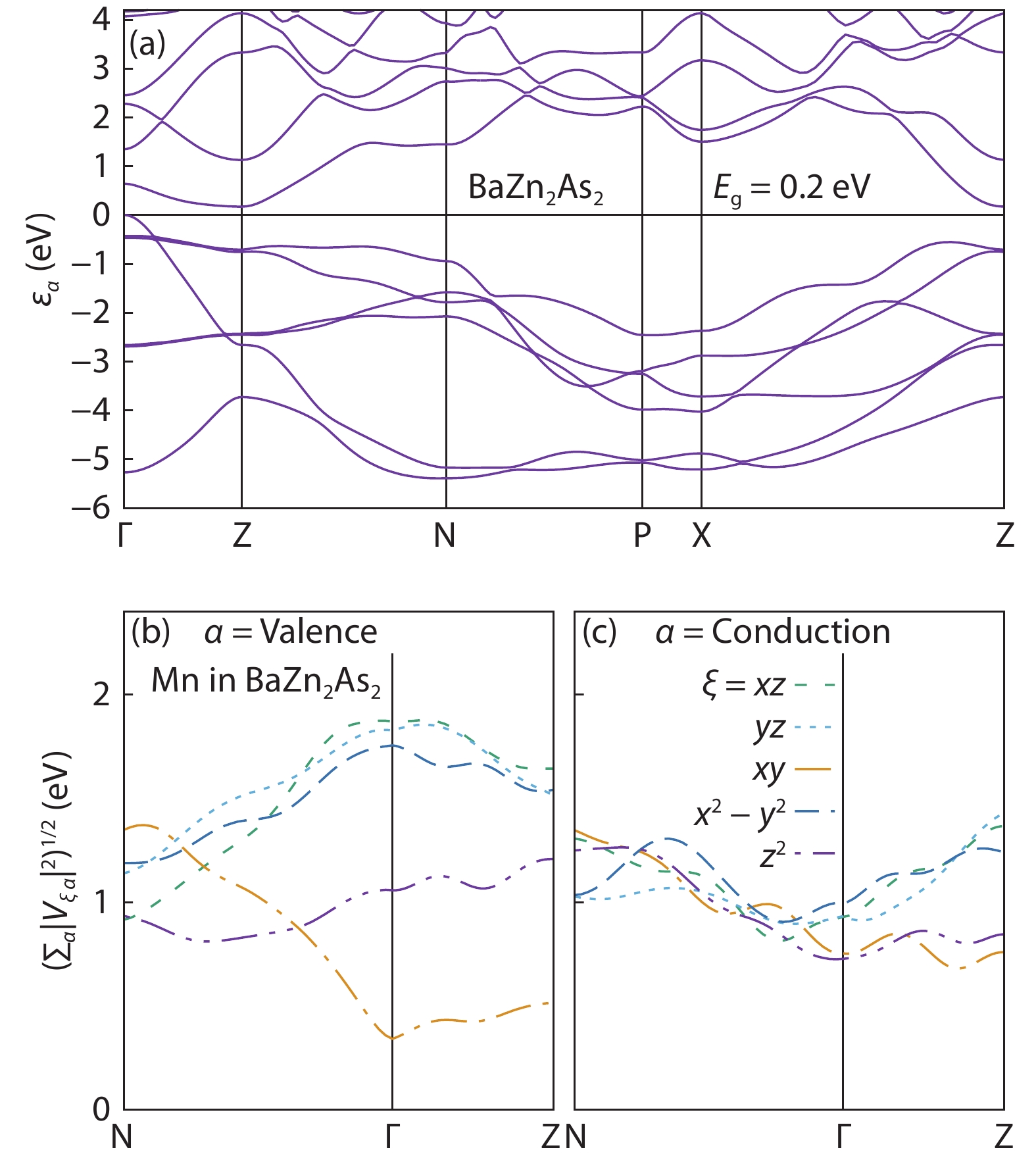
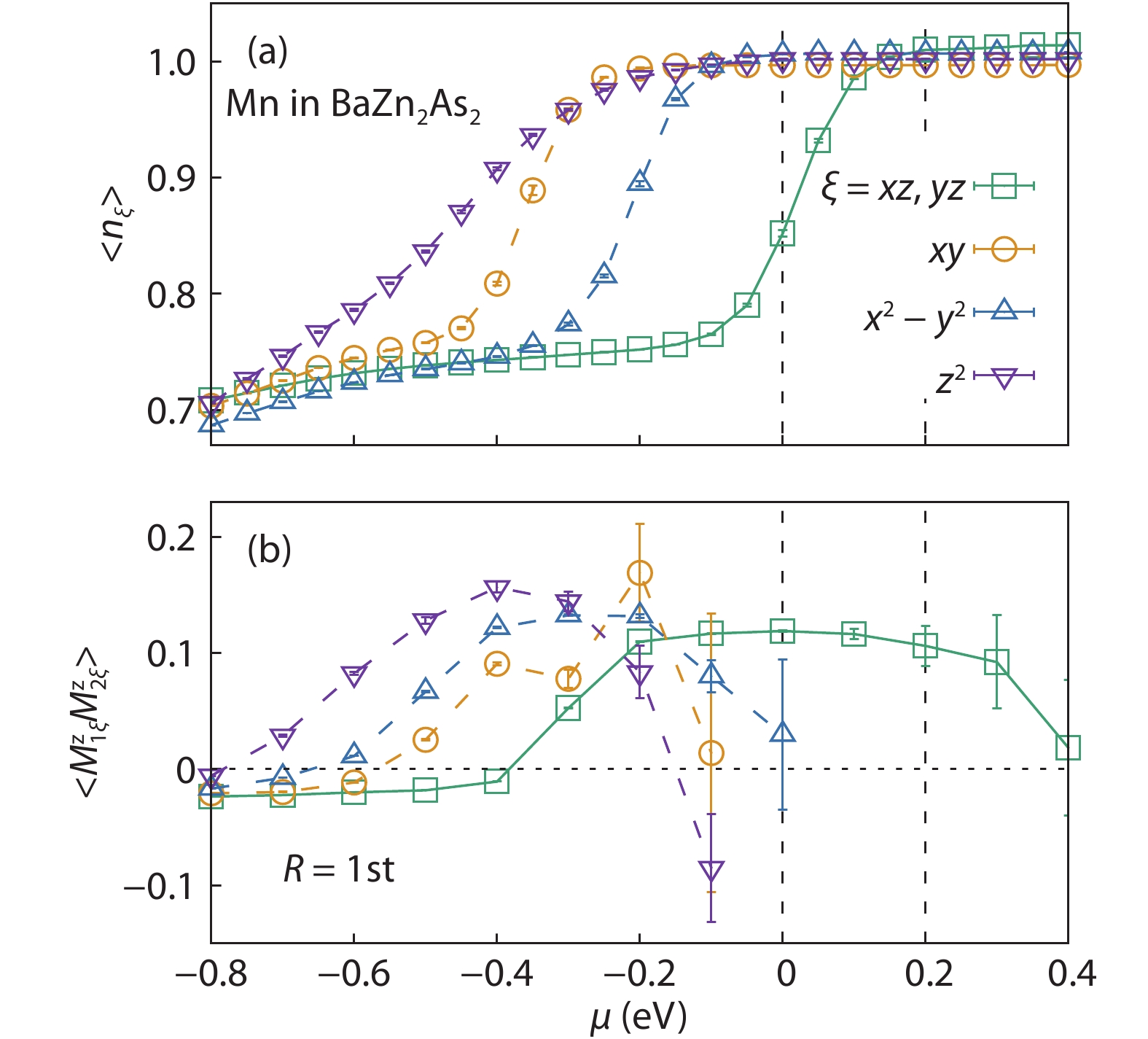
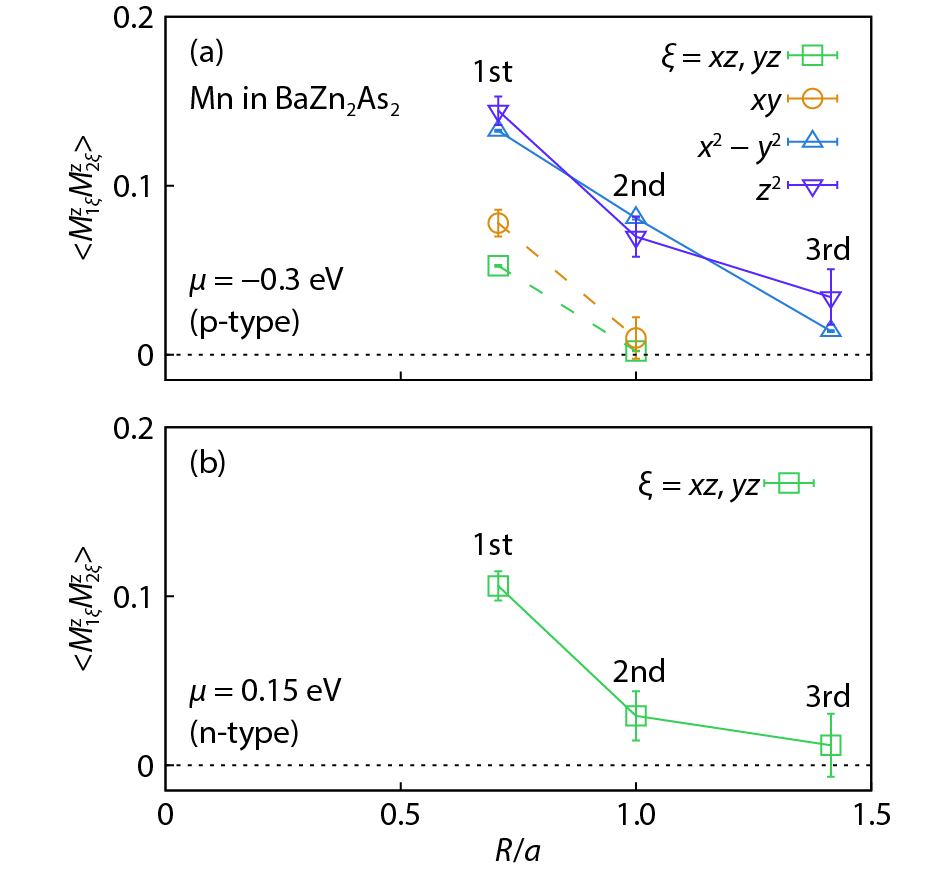
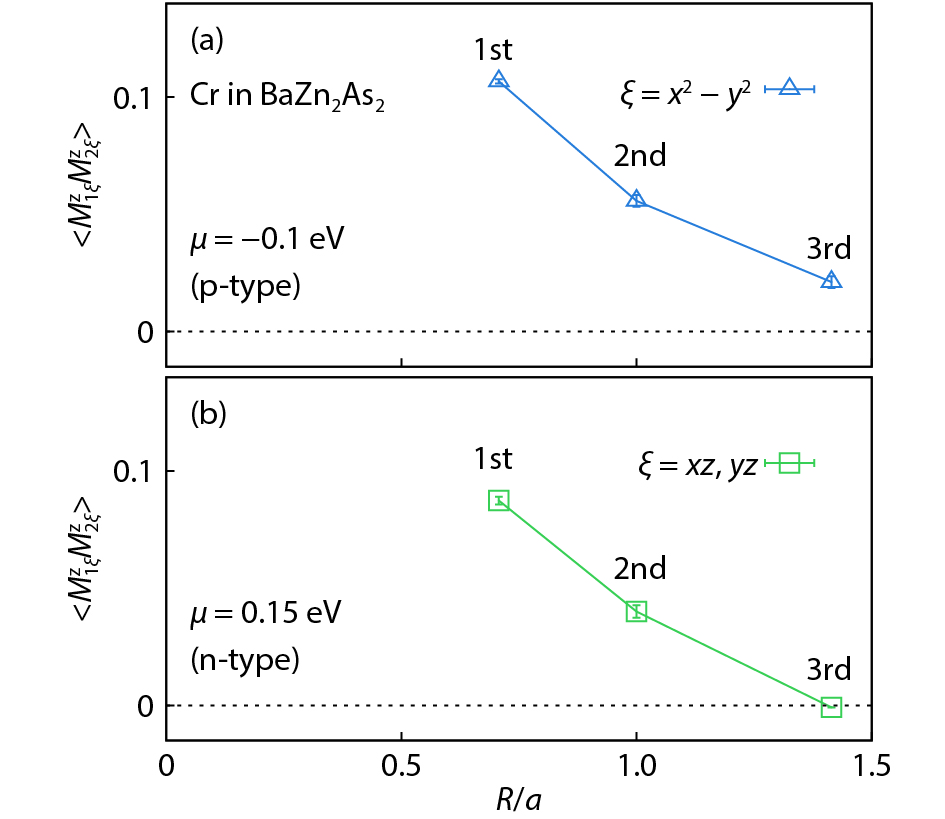
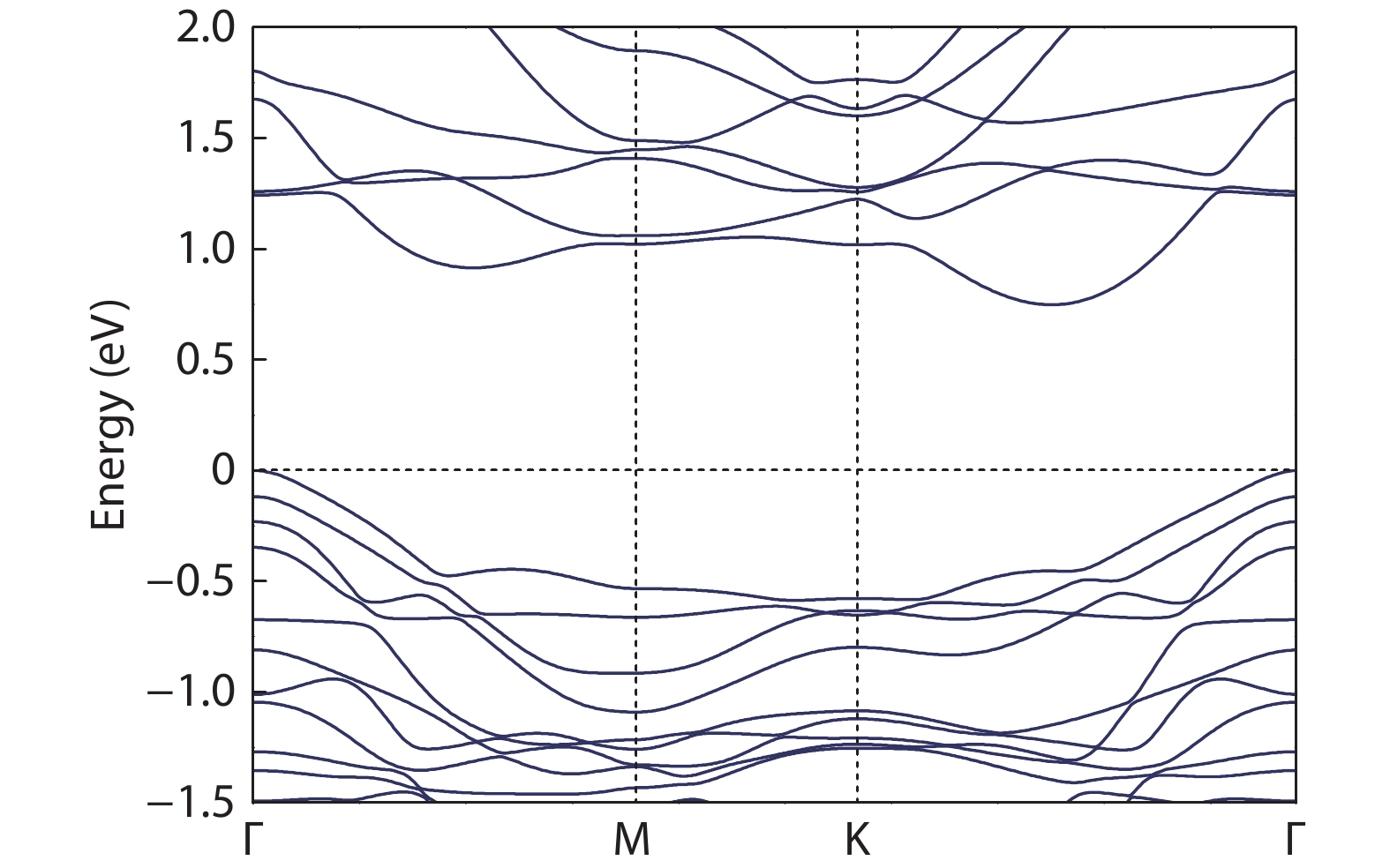
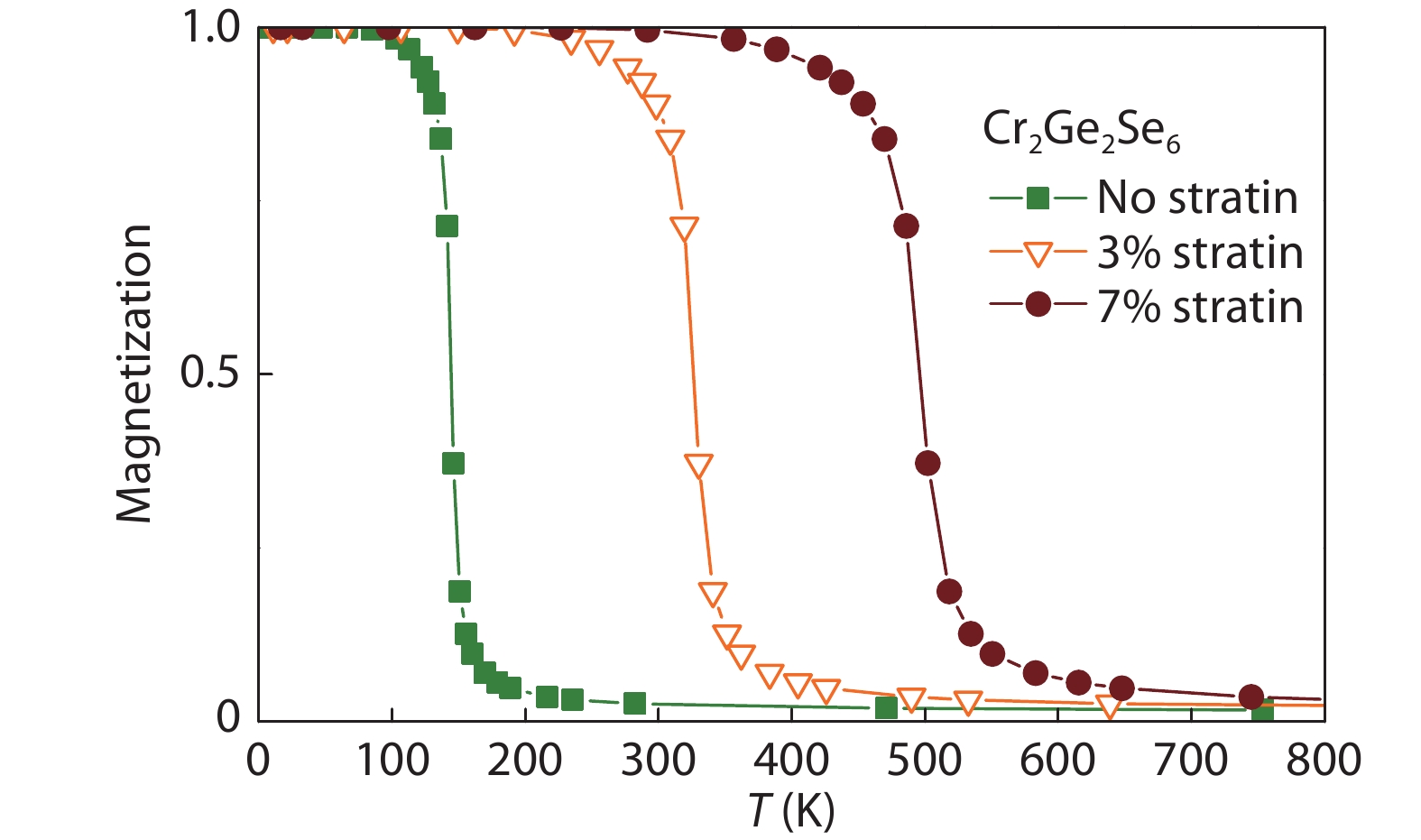
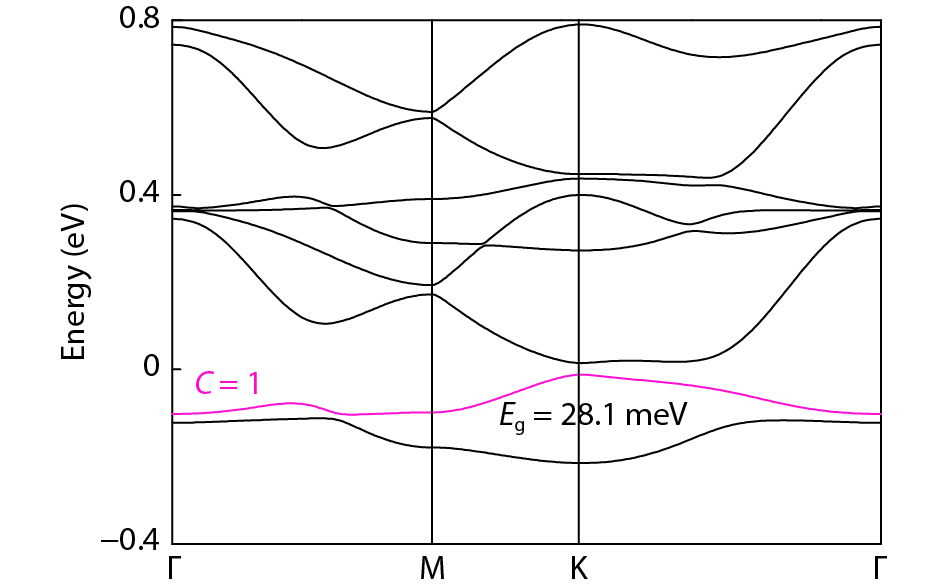
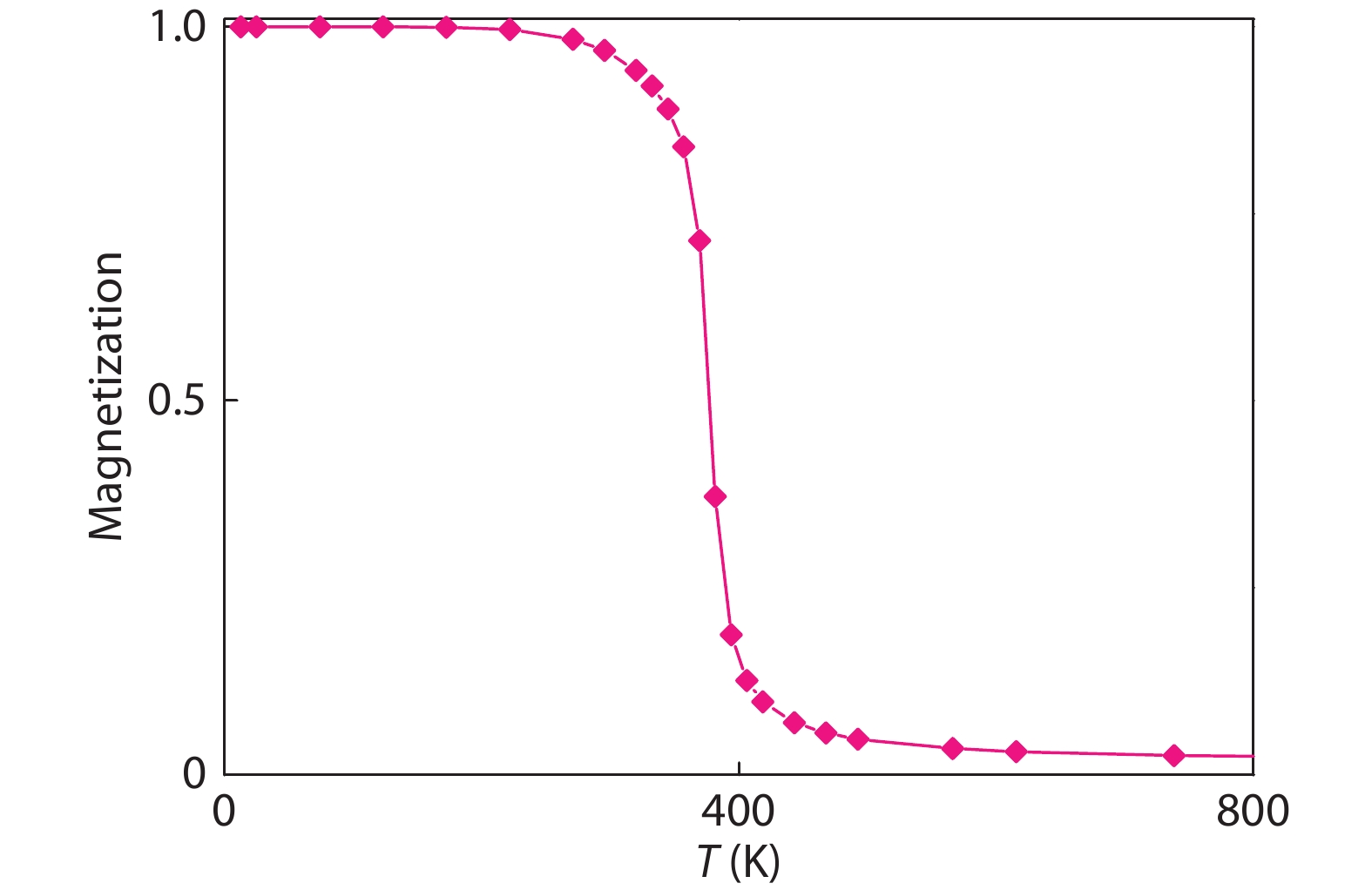
Magnetic semiconductors have been demonstrated to work at low temperatures, but not yet at room temperature for spin electronic applications. In contrast to the p-type diluted magnetic semiconductors, n-type diluted magnetic semiconductors are few. Using a combined method of the density function theory and quantum Monte Carlo simulation, we briefly discuss the recent progress to obtain diluted magnetic semiconductors with both p- and n-type carriers by choosing host semiconductors with a narrow band gap. In addition, the recent progress on two-dimensional intrinsic magnetic semiconductors with possible room temperature ferromangetism and quantum anomalous Hall effect are also discussed. -
References
[1] Maekawa S. Concepts in spin electronics. Oxford University Press, 2006[2] Maekawa S, Valenzuela S O, Saitoh E, et al. Spin current. Oxford University Press, 2012[3] Kenney D, Norman C. What don’t we know. Science, 2005, 309, 75 doi: 10.1126/science.309.5731.75[4] Ohno H. Making nonmagnetic semiconductors ferromagnetic. Science, 1998, 281, 951 doi: 10.1126/science.281.5379.951[5] Dietl T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat Mater, 2010, 9, 965 doi: 10.1038/nmat2898[6] Chen L, Yang X, Yang F, et al. Enhancing the Curie temperature of ferromagnetic semiconductor (Ga,Mn)As to 200 K via nanostructure engineering. Nano Lett, 2011, 11, 2584 doi: 10.1021/nl201187m[7] Masek J, Kudrnovsky J, Maca F, et al. Dilute moment n-type ferromagnetic semiconductor Li(Zn,Mn)As. Phys Rev Lett, 2007, 98, 067202 doi: 10.1103/PhysRevLett.98.067202[8] Deng Z, Jin C Q, Liu Q Q, et al. Li(Zn,Mn)As as a new generation ferromagnet based on a I–II–V semiconductor. Nat Commun, 2011, 2, 422 doi: 10.1038/ncomms1425[9] Deng Z, Zhao K, Gu B, et al. Diluted ferromagnetic semiconductor Li(Zn,Mn)P with decoupled charge and spin doping. Phys Rev B, 2013, 88, 081203 doi: 10.1103/PhysRevB.88.081203[10] Ding C, Man H, Qin C, et al. (La1– xBa x)(Zn1– xMn x)AsO: A two-dimensional 1111-type diluted magnetic semiconductor in bulk form. Phys Rev B, 2013, 88, 041102 doi: 10.1103/PhysRevB.88.041102[11] Zhao K, Deng Z, Wang X C, et al. New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the 122 iron-based superconductors. Nat Commun, 2013, 4, 1442 doi: 10.1038/ncomms2447[12] Zhao K, Chen B J, Zhao G Q, et al. Ferromagnetism at 230 K in (Ba0.7K0.3)(Zn0.85Mn0.15)2As2 diluted magnetic semiconductor. Chin Sci Bull, 2014, 59, 2524 doi: 10.1007/s11434-014-0398-z[13] Glasbrenner J K, Zutic I, Mazin I I. Theory of Mn-doped II–II–V semiconductors. Phys Rev B, 2014, 90, 140403 doi: 10.1103/PhysRevB.90.140403[14] Suzuki H, Zhao K, Shibata G, et al. Photoemission and X-ray absorption studies of the isostructural to Fe-based superconductors diluted magnetic semiconductor Ba1– xK x(Zn1– yMn y)2As2. Phys Rev B, 2015, 91, 140401 doi: 10.1103/PhysRevB.91.140401[15] Suzuki H, Zhao G Q, Zhao K, et al. Fermi surfaces and p-d hybridization in the diluted magnetic semiconductor Ba1– xK x- (Zn1– yMn y)2As2 studied by soft X-ray angle-resolved photoemission spectroscopy. Phys Rev B, 2015, 92, 235120 doi: 10.1103/PhysRevB.92.235120[16] Guo S, Man H, Ding C, et al. Ba(Zn,Co)2As2: A diluted ferromagnetic semiconductor with n-type carriers and isostructural to 122 iron-based superconductors. Phys Rev B, 2019, 99, 155201 doi: 10.1103/PhysRevB.99.155201[17] Gu B, Maekawa S. Diluted magnetic semiconductors with narrow band gaps. Phys Rev B, 2016, 94, 155202 doi: 10.1103/PhysRevB.94.155202[18] Gu B, Maekawa S. New p- and n-type ferromagnetic semiconductors: Cr-doped BaZn2As2. AIP Adv, 2017, 7, 055805 doi: 10.1063/1.4973208[19] Gu B, Bulut N, Maekawa S. Crystal structure effect on the ferromagnetic correlations in ZnO with magnetic impurities. J Appl Phys, 2008, 104, 103906 doi: 10.1063/1.3028262[20] Ohe J, Tomoda Y, Bulut N, et al. Combined approach of density functional theory and quantum Monte Carlo method to electron correlation in dilute magnetic semiconductors. J Phys Soc Jpn, 2009, 78, 083703 doi: 10.1143/JPSJ.78.083703[21] Gu B, Bulut, Ziman N T, et al. Possible d0 ferromagnetism in MgO doped with nitrogen. Phys Rev B, 2009, 79, 024407 doi: 10.1103/PhysRevB.79.024407[22] Ichimura M, Tanikawa K, Takahashi S, et al. Foundations of quantum mechanics in the light of new technology. Edited by S Ishioka, K Fujikawa. Singapore: World Scientific, 2006, 183[23] Bulut N, Tanikawa K, Takahashi S, et al. Long-range ferromagnetic correlations between Anderson impurities in a semiconductor host: Quantum Monte Carlo simulations. Phys Rev B, 2007, 76, 045220 doi: 10.1103/PhysRevB.76.045220[24] Tomoda Y, Bulut N, Maekawa S. Inter-impurity and impurity-host magnetic correlations in semiconductors with low-density transition-metal impurities. Physica B, 2009, 404, 1159 doi: 10.1016/j.physb.2008.11.094[25] Huang B, Clark G, Navarro-Moratalla E, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature, 2017, 546, 270 doi: 10.1038/nature22391[26] Gong C, Li L, Li Z, et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature, 2017, 546, 265 doi: 10.1038/nature22060[27] Bonilla M, Kolekar S, Ma Y, et al. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat Nanotechnol, 2018, 13, 289 doi: 10.1038/s41565-018-0063-9[28] O’Hara D J, Zhu T, Trout A H, et al. Room temperature intrinsic ferromagnetism in epitaxial manganese selenide films in the monolayer limit. Nano Lett, 2018, 18, 3125 doi: 10.1021/acs.nanolett.8b00683[29] Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev, 1964, 136, B864 doi: 10.1103/PhysRev.136.B864[30] Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects. Phys Rev, 1965, 140, A1133 doi: 10.1103/PhysRev.140.A1133[31] Hirsch J E, Fye R M. Monte Carlo method for magnetic impurities in metals. Phys Rev Lett, 1986, 56, 2521 doi: 10.1103/PhysRevLett.56.2521[32] Gu B, Gan J Y, Bulut N, et al. Quantum renormalization of the spin Hall effect. Phys Rev Lett, 2010, 105, 086401 doi: 10.1103/PhysRevLett.105.086401[33] Gu B, Sugai I, Ziman T, et al. Surface-assisted spin Hall effect in Au films with Pt impurities. Phys Rev Lett, 2010, 105, 216401 doi: 10.1103/PhysRevLett.105.216401[34] Xu Z, Gu B, Mori M, et al. Sign change of the spin Hall effect due to electron correlation in nonmagnetic CuIr alloys. Phys Rev Lett, 2015, 114, 017202 doi: 10.1103/PhysRevLett.114.017202[35] Haldane F D M, Anderson P W. Simple model of multiple charge states of transition-metal impurities in semiconductors. Phys Rev B, 1976, 13, 2553 doi: 10.1103/PhysRevB.13.2553[36] Blaha P, Schwart K, Hadsen G K H, et al. WIEN2K, an augmented plane wave plus local orbitals program for calculating crystal properties. Vienna University of Technology, Vienna, 2001[37] Tran F, Blaha P. Implementation of screened hybrid functionals based on the Yukawa potential within the LAPW basis set. Phys Rev B, 2011, 83, 235118 doi: 10.1103/PhysRevB.83.235118[38] Shein I R, Ivanovskii A L. Elastic, electronic properties and intra-atomic bonding in orthorhombic and tetragonal polymorphs of BaZn2As2 from first-principles calculations. J Alloys Compd, 2014, 583, 100 doi: 10.1016/j.jallcom.2013.08.118[39] Dong X J, You J Y, Gu B, et al. Strain-induced room-temperature ferromagnetic semiconductors with large anomalous Hall conductivity in two-dimensional Cr2Ge2Se6. Phys Rev Appl, 2019, 12, 014020 doi: 10.1103/PhysRevApplied.12.014020[40] You J Y, Zhang Z, Gu B, et al. Two-dimensional room temperature ferromagnetic semiconductors with quantum anomalous Hall effect. arXiv: 1904.11357[41] Tu N T, Hai P N, Anh L D, et al. High-temperature ferromagnetism in heavily Fe-doped ferromagnetic semiconductor (Ga,Fe)Sb. Appl Phys Lett, 2016, 108, 192401 doi: 10.1063/1.4948692[42] Tu N T, Hai P N, Anh L D, et al. A new class of ferromagnetic semiconductors with high Curie temperatures. arXiv: 1706.00735[43] Kudrin A V, Danilov Y A, Lesnikov V P, et al. High-temperature intrinsic ferromagnetism in the (In,Fe)Sb semiconductor. J Appl Phys, 2017, 122, 183901 doi: 10.1063/1.5010191[44] Tu N T, Hai P N, Anh L D, et al. Electrical control of ferromagnetism in the n-type ferromagnetic semiconductor (In,Fe)Sb with high Curie temperature. Appl Phys Lett, 2018, 112, 122409 doi: 10.1063/1.5022828[45] Burch K S, Mandrus D, Park J G. Magnetism in two-dimensional van der Waals materials. Nature, 2018, 563, 47 doi: 10.1038/s41586-018-0631-z -
Proportional views






 DownLoad:
DownLoad: