| Citation: |
R. Rahaman, M. Sharmin, J. Podder. Band gap tuning and p to n-type transition in Mn-doped CuO nanostructured thin films[J]. Journal of Semiconductors, 2022, 43(1): 012801. doi: 10.1088/1674-4926/43/1/012801
****
R Rahaman, M Sharmin, J Podder, Band gap tuning and p to n-type transition in Mn-doped CuO nanostructured thin films[J]. J. Semicond., 2022, 43(1): 012801. doi: 10.1088/1674-4926/43/1/012801.
|
Band gap tuning and p to n-type transition in Mn-doped CuO nanostructured thin films
DOI: 10.1088/1674-4926/43/1/012801
More Information
-
Abstract
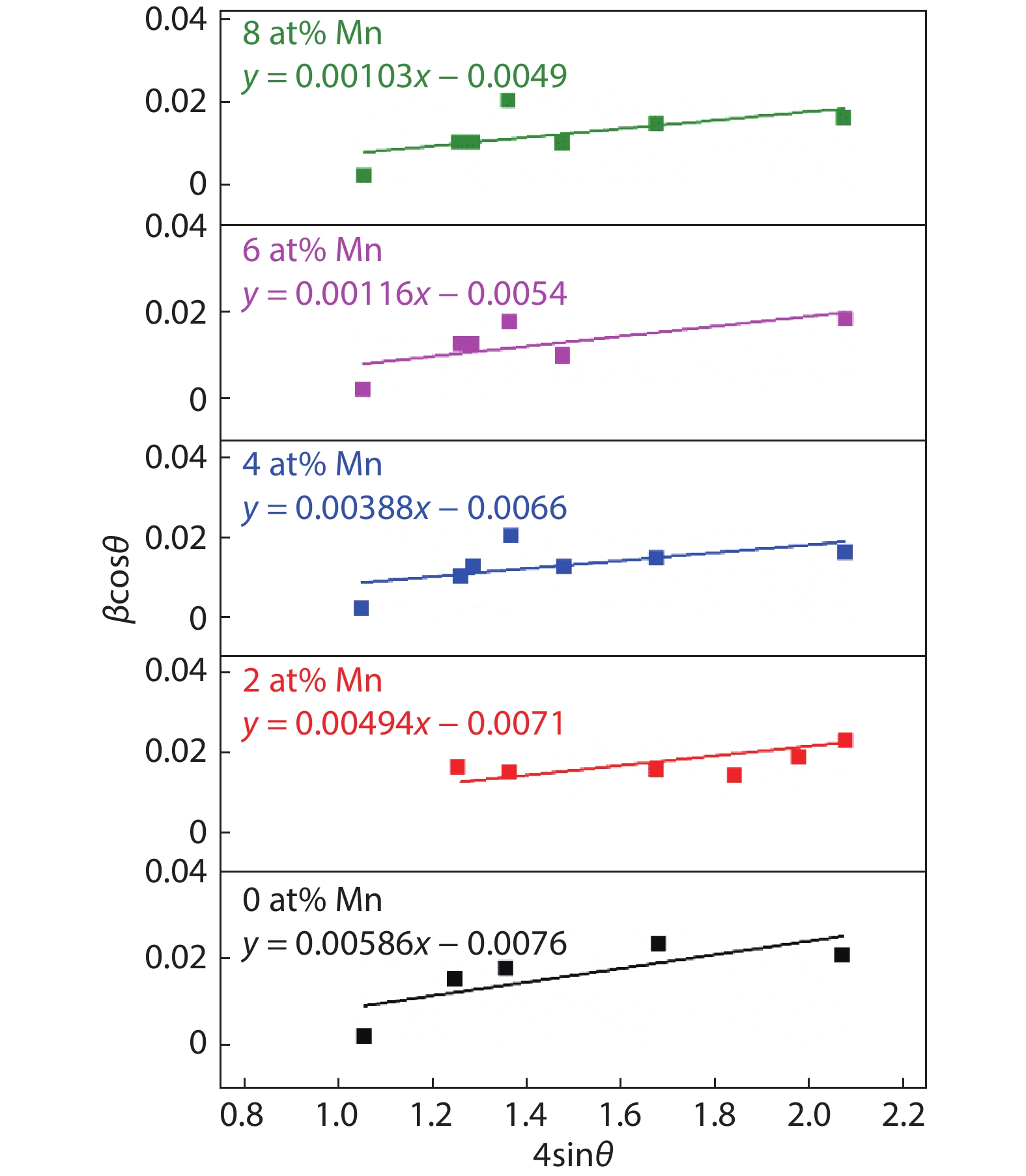
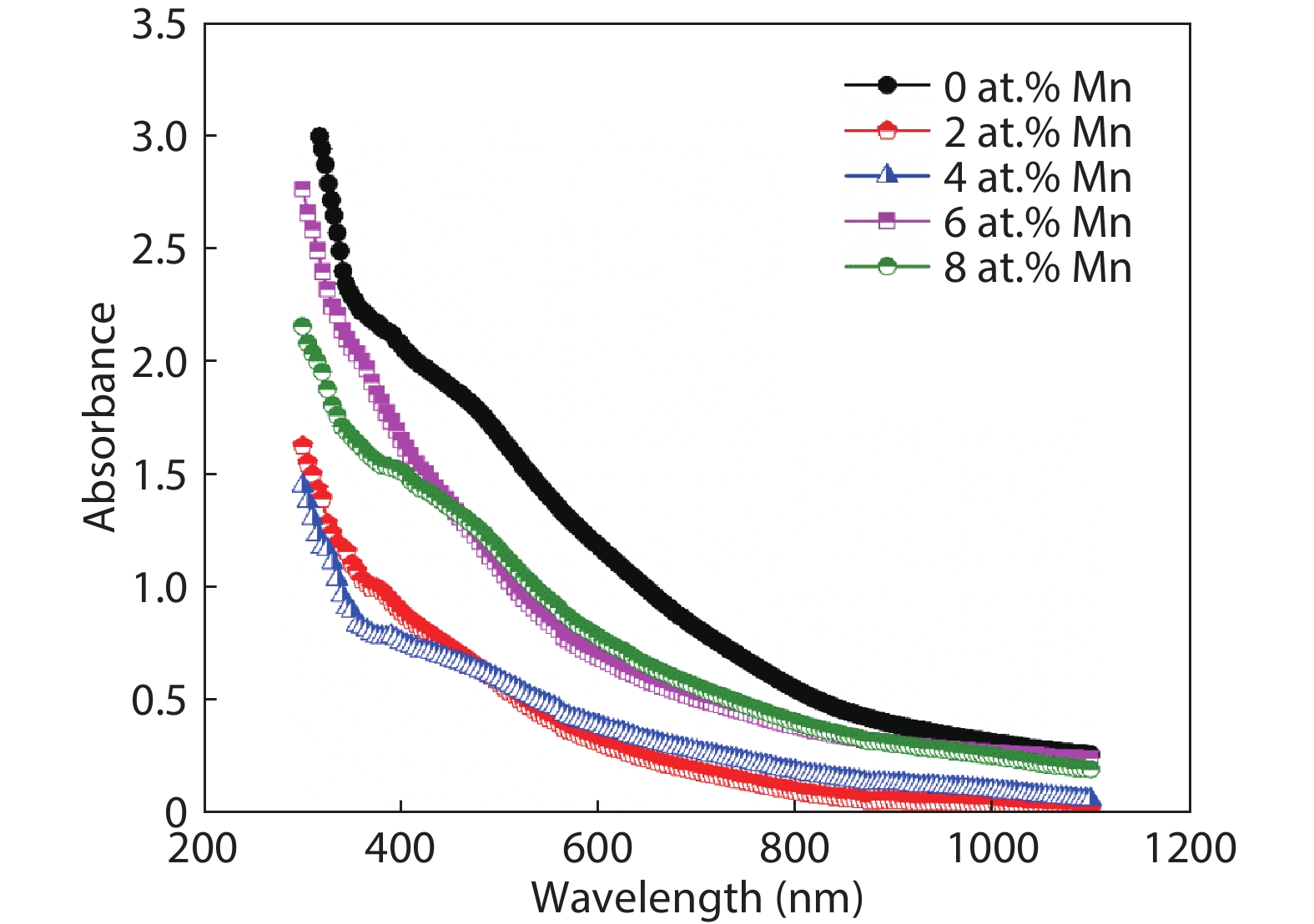
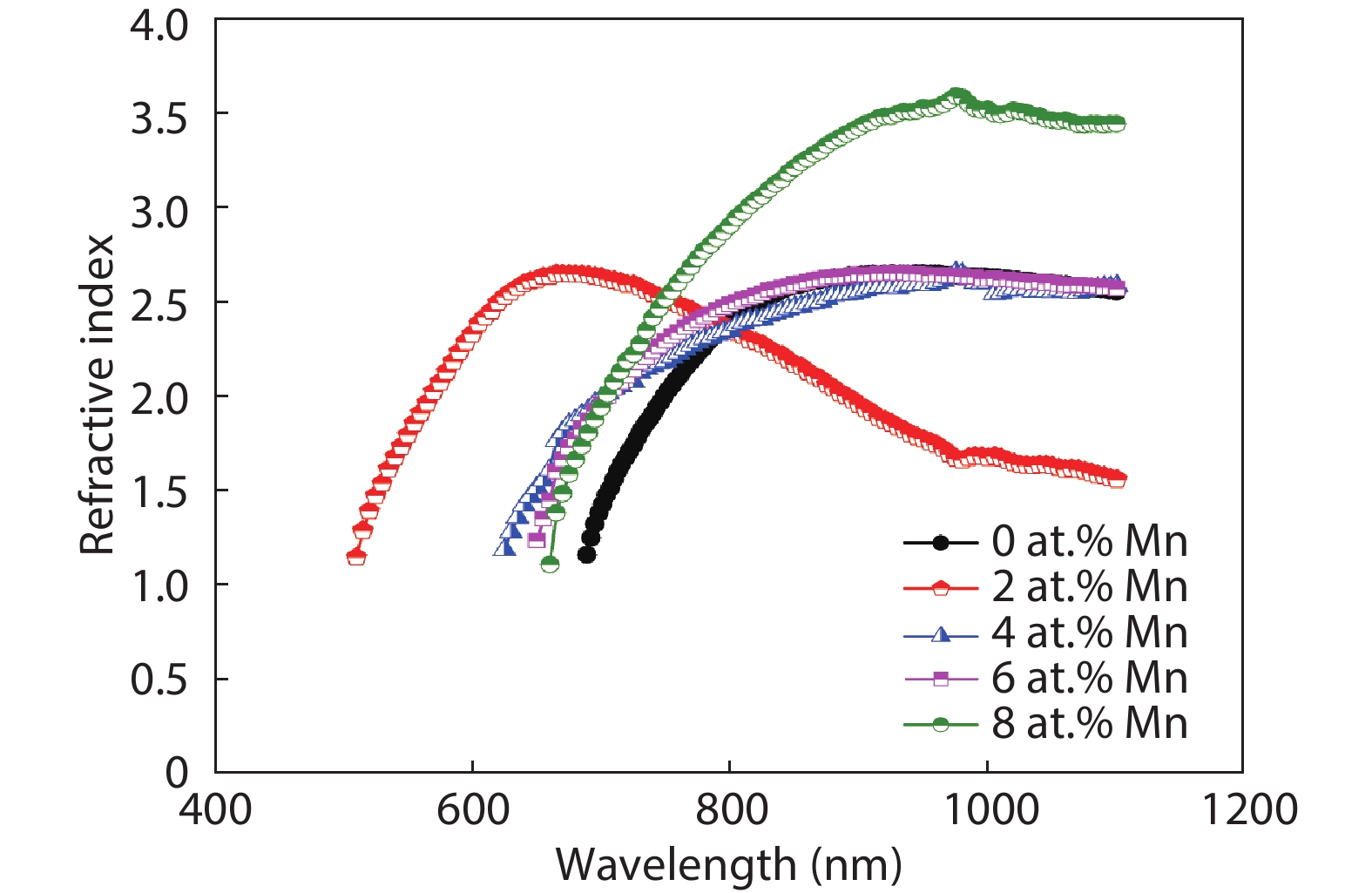
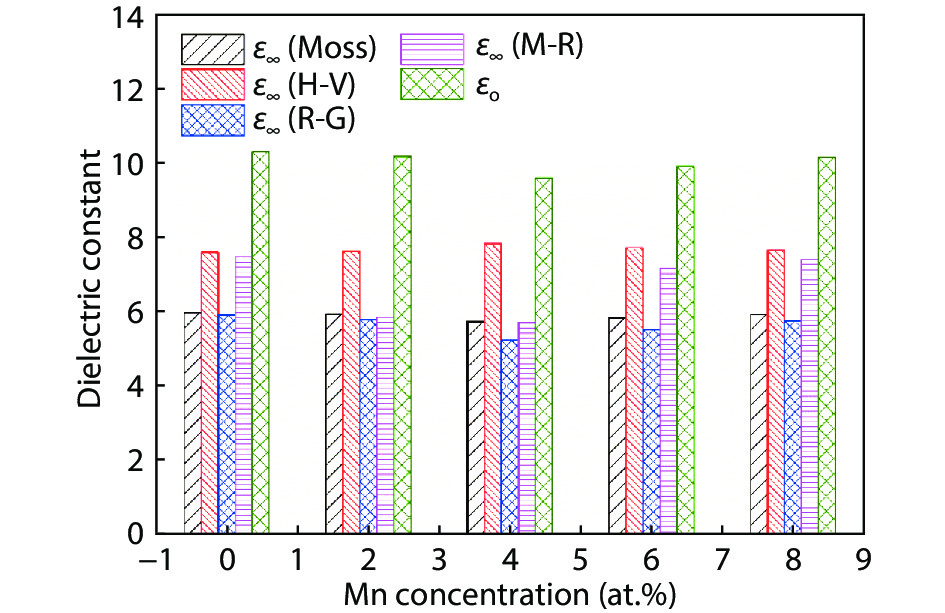
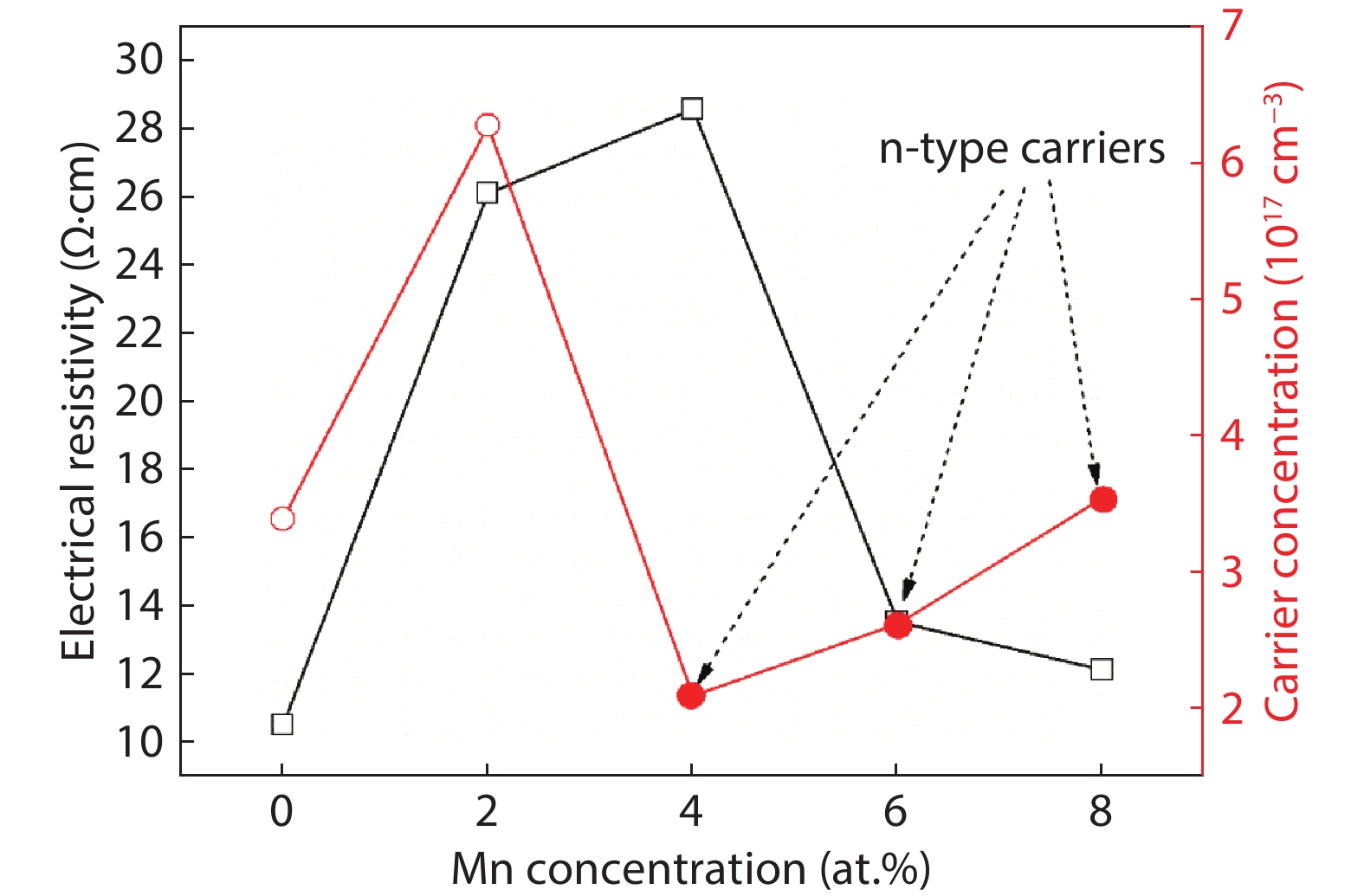
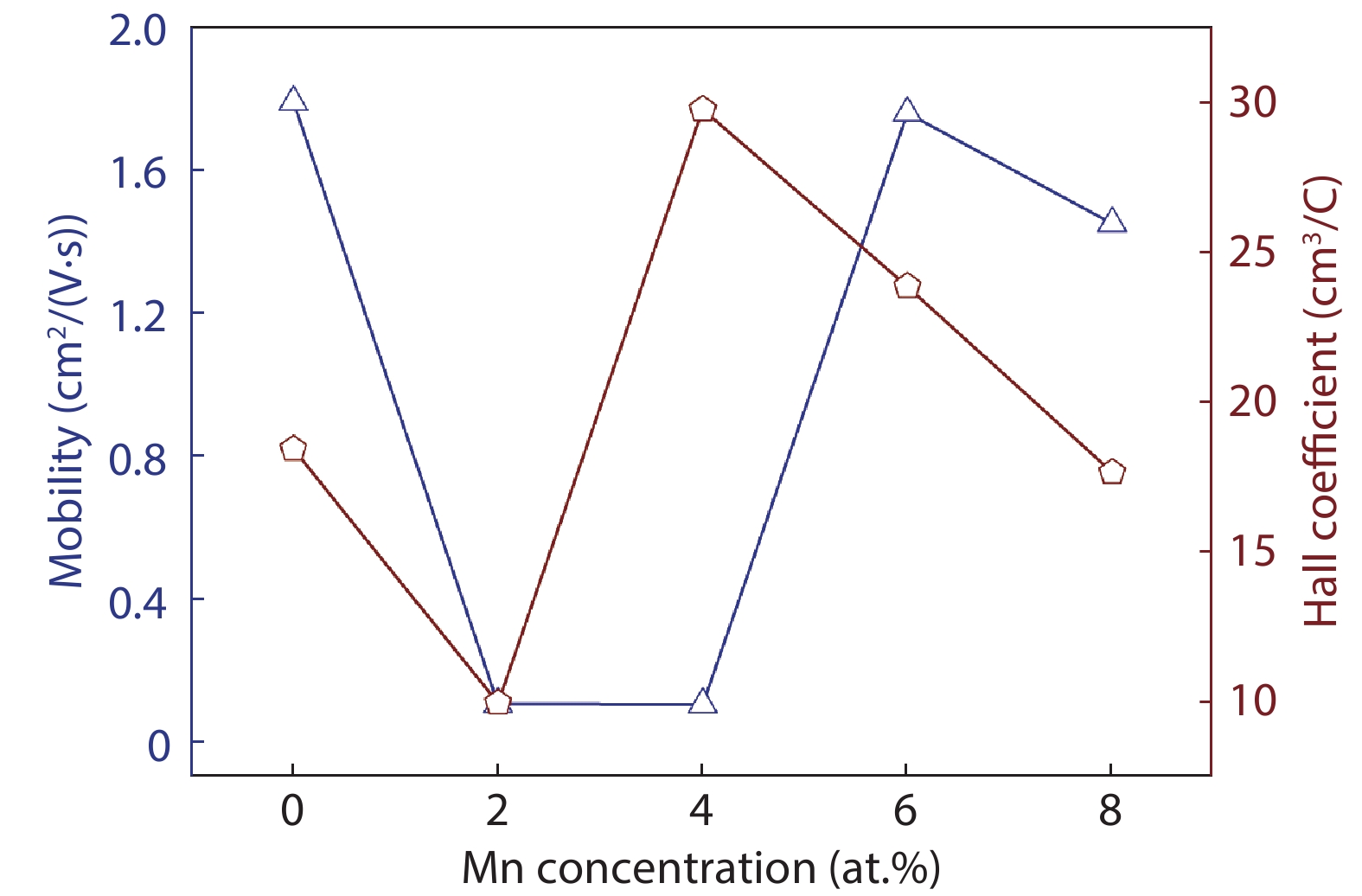
Here we discuss the synthesis of copper (II) oxide (CuO) and manganese (Mn)-doped CuO thin films varying with 0 to 8 at% Mn using the spray pyrolysis technique. As-deposited film surfaces comprised of agglomerated spherical nanoparticles and a semi-spongy porous structure for 4 at% Mn doping. Energy dispersive analysis of X-rays confirmed the chemical composition of the films. X-ray diffraction spectra showed a polycrystalline monoclinic structure with the predominance of the ($ {\overline 1} $ 11) peak. Optical band gap energy for direct and indirect transitions was estimated in the ranges from 2.67–2.90 eV and 0.11–1.73 eV, respectively. Refractive index and static dielectric constants were computed from the optical spectra. Electrical resistivity of CuO and Mn-doped CuO (Mn:CuO) thin films was found in the range from 10.5 to 28.6 Ω·cm. The tiniest electron effective mass was calculated for 4 at% Mn:CuO thin films. P to n-type transition was observed for 4 at% Mn doping in CuO films. Carrier concentration and mobility were found in the orders of 1017 cm–3 and 10–1 cm2/(V·s), respectively. The Hall coefficient was found to be between 9.9 and 29.8 cm3/C. The above results suggest the suitability of Mn:CuO thin films in optoelectronic applications.-
Keywords:
- Mn:CuO,
- spray pyrolysis,
- FESEM,
- XRD,
- band gap,
- Hall effect
-
References
[1] Yoon K H, Choi W J, Kang D H. Photoelectrochemical properties of copper oxide thin films coated on an n-Si substrate. Thin Solid Films, 2000, 372, 250 doi: 10.1016/S0040-6090(00)01058-0[2] de Los Santos Valladares L, Salinas D H, Dominguez A B, et al. Crystallization and electrical resistivity of Cu2O and CuO obtained by thermal oxidation of Cu thin films on SiO2/Si substrates. Thin Solid Films, 2012, 520, 6368 doi: 10.1016/j.tsf.2012.06.043[3] Chang S S, Lee H J, Park H J. Photoluminescence properties of spark-processed CuO. Ceram Int, 2005, 31, 411 doi: 10.1016/j.ceramint.2004.05.027[4] Han K, Tao M. Electrochemically deposited p-n homojunction cuprous oxide solar cells. Sol Energy Mater Sol Cells, 2009, 93, 153 doi: 10.1016/j.solmat.2008.09.023[5] Steinhauer S, Brunet E, Maier T, et al. Gas sensing properties of novel CuO nanowire devices. Sens Actuators B, 2013, 187, 50 doi: 10.1016/j.snb.2012.09.034[6] Ren G G, Hu D W, Cheng E W C, et al. Characterisation of copper oxide nanoparticles for antimicrobial applications. Int J Antimicrob Agents, 2009, 33, 587 doi: 10.1016/j.ijantimicag.2008.12.004[7] Erdoğan İ Y, Güllü Ö. Optical and structural properties of CuO nanofilm: Its diode application. J Alloys Compd, 2010, 492, 378 doi: 10.1016/j.jallcom.2009.11.109[8] Al-Kuhaili M F. Characterization of copper oxide thin films deposited by the thermal evaporation of cuprous oxide (Cu2O). Vacuum, 2008, 82, 623 doi: 10.1016/j.vacuum.2007.10.004[9] Kikuchi N, Tonooka K. Electrical and structural properties of Ni-doped Cu2O films prepared by pulsed laser deposition. Thin Solid Films, 2005, 486, 33 doi: 10.1016/j.tsf.2004.12.044[10] Eisermann S, Kronenberger A, Laufer A, et al. Copper oxide thin films by chemical vapor deposition: Synthesis, characterization and electrical properties. Phys Status Solidi A, 2012, 209, 531 doi: 10.1002/pssa.201127493[11] Brazdeikis A, Karlsson U O, Flodström A S. An atomic force microscopy study of thin copper oxide films grown by molecular beam epitaxy on MgO(100). Thin Solid Films, 1996, 281/282, 57 doi: 10.1016/0040-6090(96)08574-4[12] Perednis D, Gauckler L J. Thin film deposition using spray pyrolysis. J Electroceramics, 2005, 14, 103 doi: 10.1007/s10832-005-0870-x[13] Nesa M, Sharmin M, Hossain K S, et al. Structural, morphological, optical and electrical properties of spray deposited zinc doped copper oxide thin films. J Mater Sci: Mater Electron, 2017, 28, 12523 doi: 10.1007/s10854-017-7075-3[14] Gülen Y, Bayansal F, Şahin B, et al. Fabrication and characterization of Mn-doped CuO thin films by the SILAR method. Ceram Int, 2013, 39, 6475 doi: 10.1016/j.ceramint.2013.01.077[15] Bayansal F, Taşköprü T, Şahin B, et al. Effect of cobalt doping on nanostructured CuO thin films. Metall And Mat Trans A, 2014, 45, 3670 doi: 10.1007/s11661-014-2306-1[16] Shannon R D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr Sect A, 1976, 32, 751 doi: 10.1107/S0567739476001551[17] Zhao F, Qiu H M, Pan L Q, et al. Ferromagnetism analysis of Mn-doped CuO thin films. J Phys: Condens Matter, 2008, 20, 425208 doi: 10.1088/0953-8984/20/42/425208[18] Li L, Lv B, Wang S, et al. Magnetic study of heavily Mn-doped CuO thin films. J Korean Phys Soc, 2013, 62, 1530 doi: 10.3938/jkps.62.1530[19] Ganesan K P, Anandhan N, Gopu G, et al. An enhancement of ferromagnetic, structural, morphological, and optical properties of Mn-doped Cu2O thin films by an electrodeposition technique. J Mater Sci: Mater Electron, 2019, 30, 19524 doi: 10.1007/s10854-019-02318-5[20] Durai G, Kuppusami P, Viswanathan K. Investigation on microstructure and improved supercapacitive performance of Mn doped CuO thin films prepared by reactive radio frequency magnetron sputtering. J Mater Sci: Mater Electron, 2018, 29, 2051 doi: 10.1007/s10854-017-8118-5[21] Mishjil K A, Qader K, Jabbar W A. Study the effect of Mn:CuO thin film on its optical properties. Mater Sci, 2015, 13, 388[22] Albert manoharan A, Chandramohan R, David prabu R, et al. Facile synthesis and characterization of undoped, Mn doped and Nd co-doped CuO nanoparticles for optoelectronic and magnetic applications. J Mol Struct, 2018, 1171, 388 doi: 10.1016/j.molstruc.2018.06.018[23] Tolansky S. Multiple beam interferometry of surfaces and films. London: Oxford Clarendon Press, 1948[24] Iqbal M, Thebo A A, Shah A H, et al. Influence of Mn-doping on the photocatalytic and solar cell efficiency of CuO nanowires. Inorg Chem Commun, 2017, 76, 71 doi: 10.1016/j.inoche.2016.11.023[25] Babu M H, Podder J, Dev B C, et al. P to n-type transition with wide blue shift optical band gap of spray synthesized Cd doped CuO thin films for optoelectronic device applications. Surf Interfaces, 2020, 19, 100459 doi: 10.1016/j.surfin.2020.100459[26] Chtouki T, Taboukhat S, Kavak H, et al. Characterization and third harmonic generation calculations of undoped and doped spin-coated multilayered CuO thin films. J Phys Chem Solids, 2019, 124, 60 doi: 10.1016/j.jpcs.2018.08.035[27] Lupan O, Cretu V, Postica V, et al. Enhanced ethanol vapour sensing performances of copper oxide nanocrystals with mixed phases. Sens Actuators B., 2016, 224, 434 doi: 10.1016/j.snb.2015.10.042[28] Scherrer P. Bestimmung der inneren Struktur und der Größe von Kolloidteilchen mittels Röntgenstrahlen. Kolloidchemie Ein Lehrbuch. Berlin, Heidelberg: Springer, 1912, 387 doi: 10.1007/978-3-662-33915-2_7[29] Zhao Y S, Zhang J Z. Microstrain and grain-size analysis from diffraction peak width and graphical derivation of high-pressure thermomechanics. J Appl Cryst, 2008, 41, 1095 doi: 10.1107/S0021889808031762[30] Smallman R E, Westmacott K H. Stacking faults in face-centred cubic metals and alloys. Philos Mag A, 1957, 2, 669 doi: 10.1080/14786435708242709[31] Williamson G K, Smallman R E. III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray Debye-scherrer spectrum. Philos Mag A, 1956, 1, 34 doi: 10.1080/14786435608238074[32] Tauc J. Optical properties of amorphous semiconductors. Amorphous and Liquid Semiconductors. Boston, MA: Springer, 1974, 159 doi: 10.1007/978-1-4615-8705-7_4[33] Zheng W F, Chen Y, Peng X H, et al. The phase evolution and physical properties of binary copper oxide thin films prepared by reactive magnetron sputtering. Materials, 2018, 11, 1253 doi: 10.3390/ma11071253[34] Alajlani Y, Placido F, Barlow A, et al. Characterisation of Cu2O, Cu4O3, and CuO mixed phase thin films produced by microwave-activated reactive sputtering. Vacuum, 2017, 144, 217 doi: 10.1016/j.vacuum.2017.08.005[35] Moss T S. Photoconductivity in the elements. New York: Academic Press Inc, 1952 doi: 10.1088/0370-1298/64/6/113[36] Hervé P, Vandamme L K J. General relation between refractive index and energy gap in semiconductors. Infrared Phys Technol, 1994, 35, 609 doi: 10.1016/1350-4495(94)90026-4[37] Ravindra N M, Ganapathy P, Choi J. Energy gap-refractive index relations in semiconductors - An overview. Infrared Phys Technol, 2007, 50, 21 doi: 10.1016/j.infrared.2006.04.001[38] Moumen A, Hartiti B, Thevenin P, et al. Synthesis and characterization of CuO thin films grown by chemical spray pyrolysis. Opt Quantum Electron, 2017, 49, 1 doi: 10.1007/s11082-016-0848-8[39] Dhanasekaran V, Mahalingam T. Electrochemical and physical properties of electroplated CuO thin films. J Nanosci Nanotechnol, 2013, 13, 250 doi: 10.1166/jnn.2013.6709[40] Hummel R E. Hummel R E. Electronic properties of materials. New York, NY: Springer, 2011 doi: 10.1007/978-1-4419-8164-6[41] Adachi S. Properties of group-IV, III-V and II-VI semiconductors. Chichester, UK: John Wiley & Sons, Ltd, 2005 doi: 10.1002/0470090340[42] Akaltun Y. Effect of thickness on the structural and optical properties of CuO thin films grown by successive ionic layer adsorption and reaction. Thin Solid Films, 2015, 594, 30 doi: 10.1016/j.tsf.2015.10.003[43] Güneri E. The role of Au doping on the structural and optical properties of Cu2O films. J Nano Res, 2019, 58, 49 doi: 10.4028/www.scientific.net/JNanoR.58.49[44] Baturay S, Tombak A, Kaya D, et al. Modification of electrical and optical properties of CuO thin films by Ni doping. J Sol Gel Sci Technol, 2016, 78, 422 doi: 10.1007/s10971-015-3953-4[45] Sanal K C, Vikas L S, Jayaraj M K. Room temperature deposited transparent p-channel CuO thin film transistors. Appl Surf Sci, 2014, 297, 153 doi: 10.1016/j.apsusc.2014.01.109[46] Shen Y L, Guo M L, Xia X H, et al. Role of materials chemistry on the electrical/electronic properties of CuO thin films. Acta Mater, 2015, 85, 122 doi: 10.1016/j.actamat.2014.11.018 -
Proportional views







 DownLoad:
DownLoad: