| Citation: |
M. Benaida, K. E. Aiadi, S. Mahtout, S. Djaadi, W. Rammal, M. Harb. Growth behavior and electronic properties of Gen + 1 and AsGen (n = 1–20) clusters: a DFT study[J]. Journal of Semiconductors, 2019, 40(3): 032101. doi: 10.1088/1674-4926/40/3/032101
****
M Benaida, K E Aiadi, S Mahtout, S Djaadi, W Rammal, M Harb, Growth behavior and electronic properties of Gen + 1 and AsGen (n = 1–20) clusters: a DFT study[J]. J. Semicond., 2019, 40(3): 032101. doi: 10.1088/1674-4926/40/3/032101.
|
Growth behavior and electronic properties of Gen + 1 and AsGen (n = 1–20) clusters: a DFT study
DOI: 10.1088/1674-4926/40/3/032101
More Information
-
Abstract
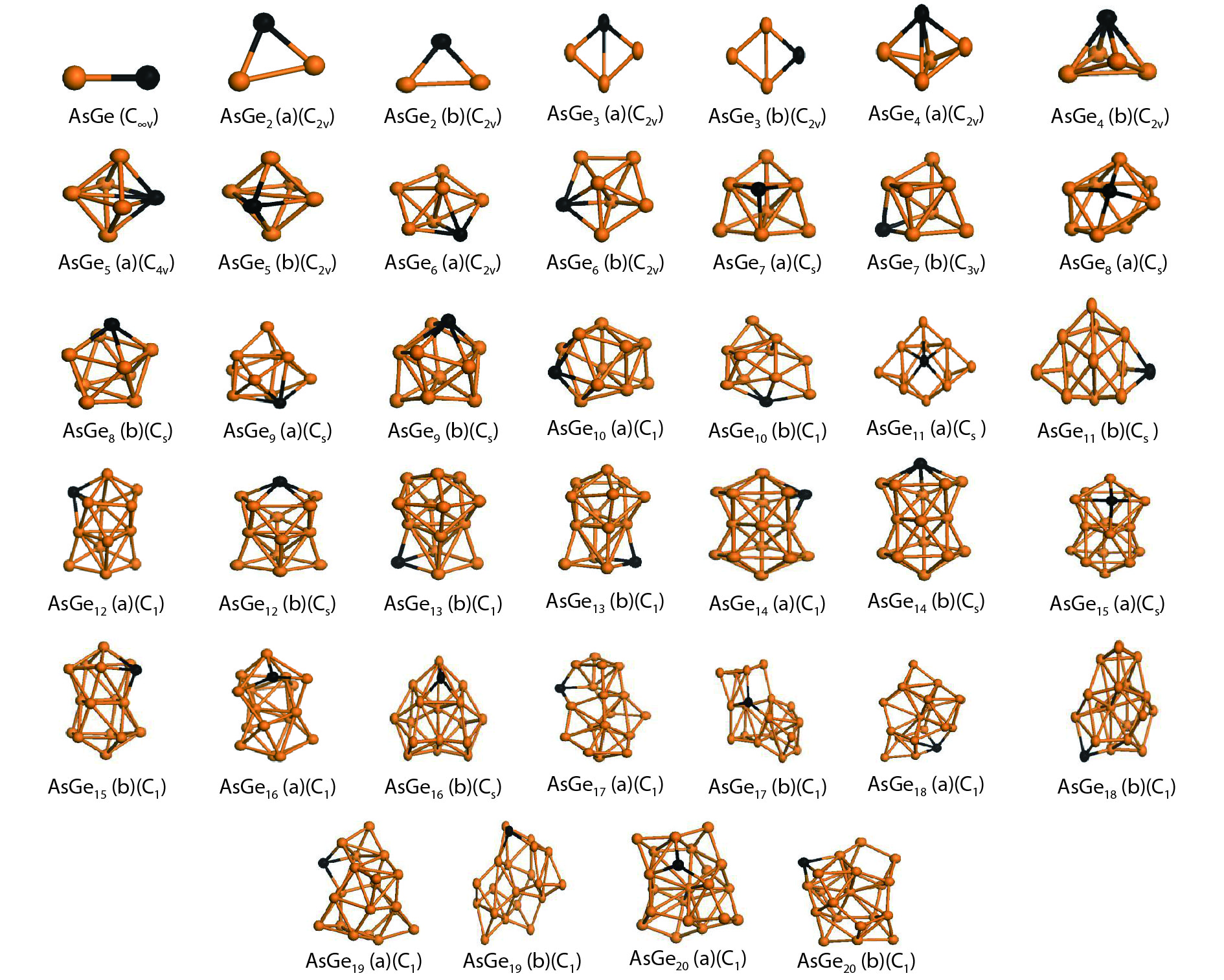
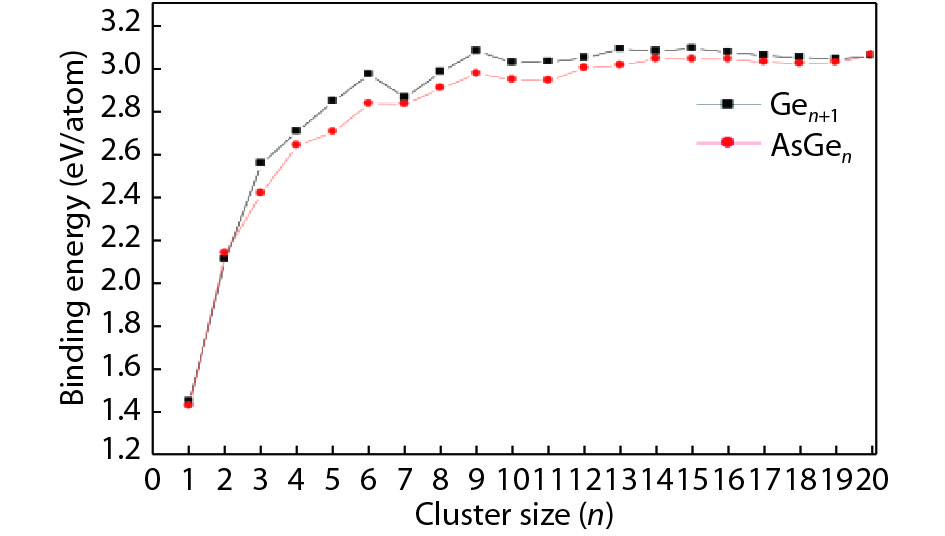
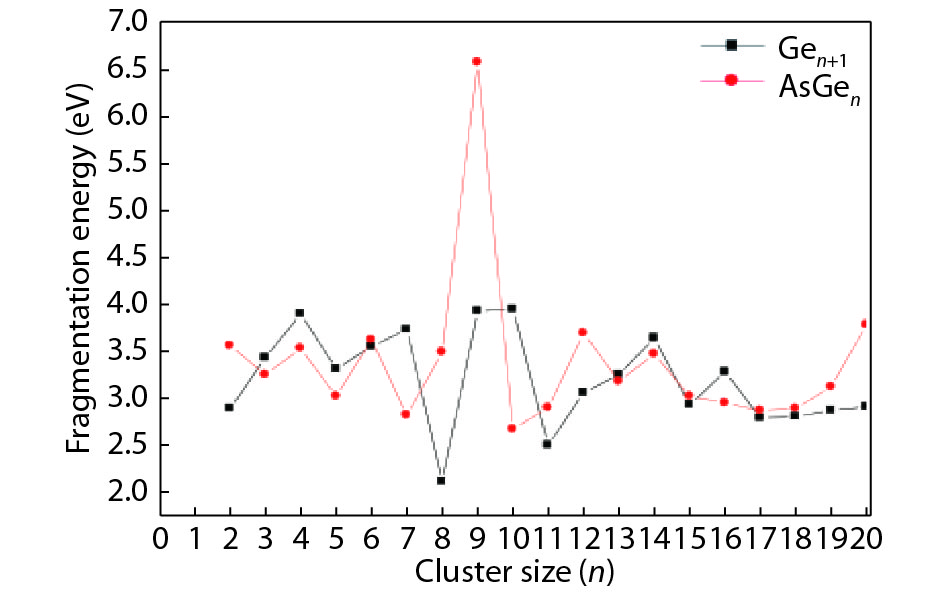
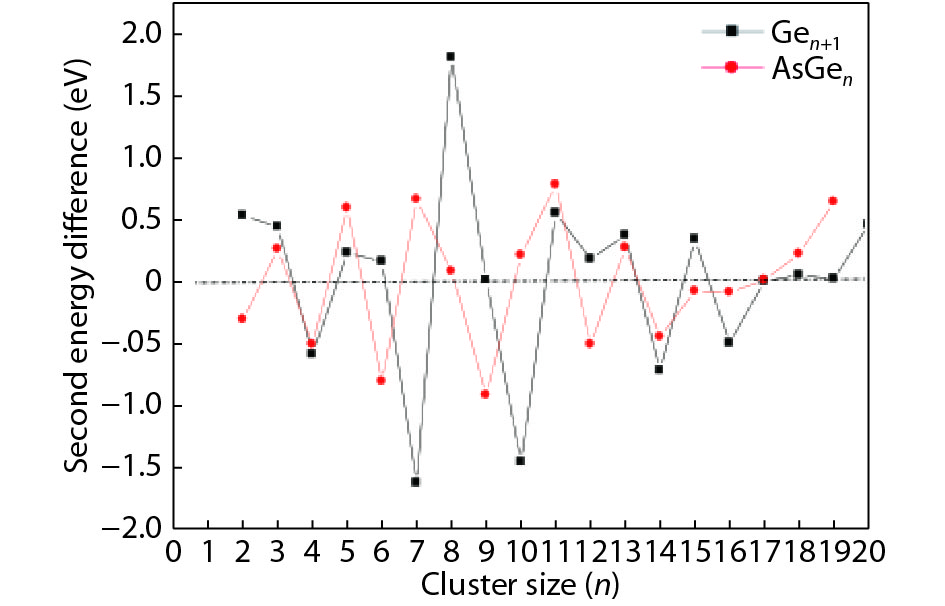
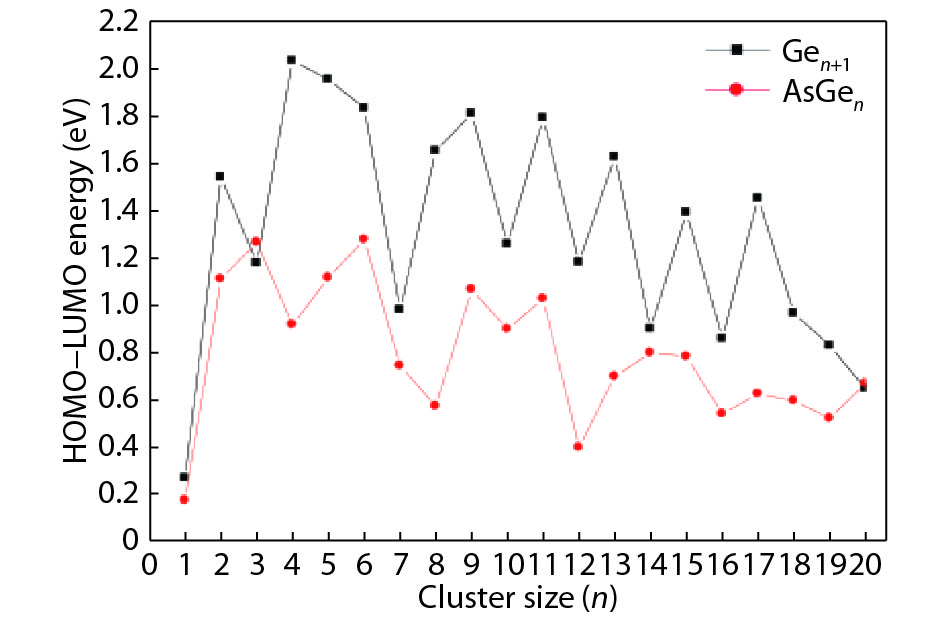
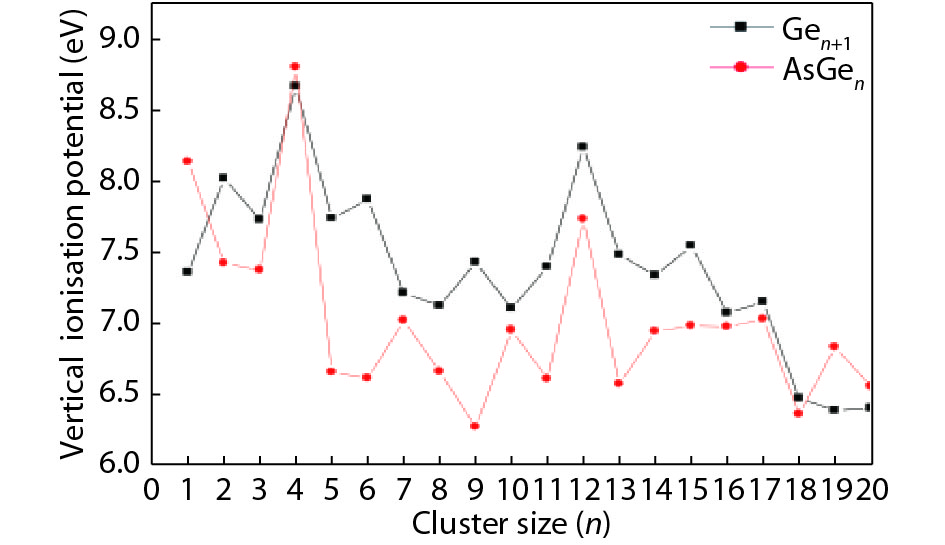
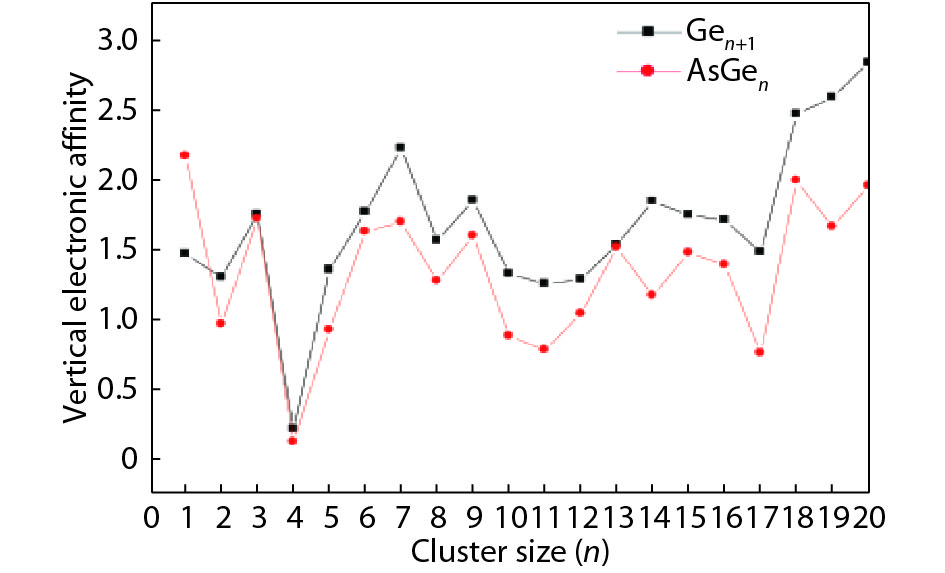
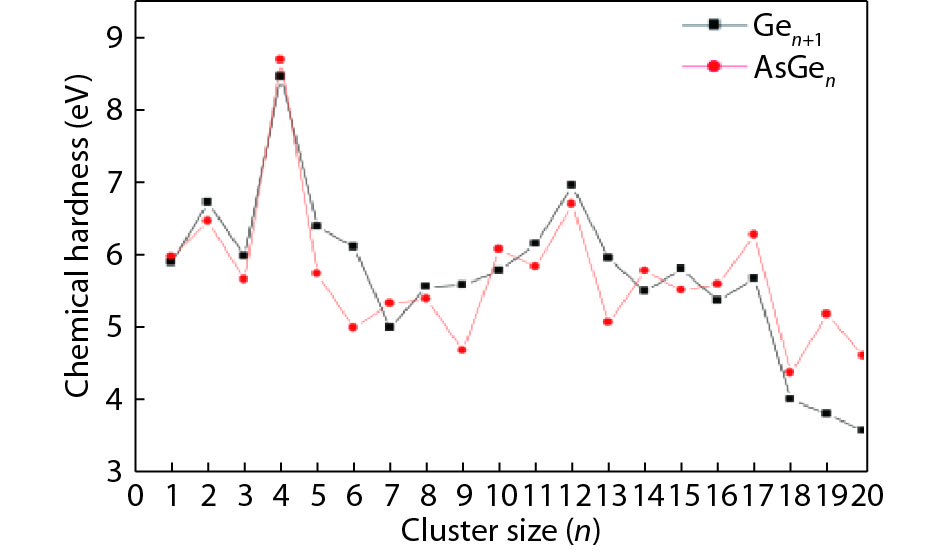
We present a systematic computational study based on the density functional theory (DFT) aiming to high light the possible effects of one As doping atom on the structural, energetic, and electronic properties of different isomers of Gen + 1 clusters with n = 1–20 atoms. By considering a large number of structures for each cluster size, the lowest-energy isomers are determined. The lowest-energy isomers reveal three-dimensional structures starting from n = 5. Their relative stability versus atomic size is examined based on the calculated binding energy, fragmentation energy, and second-order difference of energy. Doping Gen + 1 clusters with one As atom does not improve their stability. The electronic properties as a function of the atomic size are also discussed from the calculated HOMO–LUMO energy gap, vertical ionization potential, vertical electron affinity, and chemical hardness. The obtained results are significantly affected by the inclusion of one As atom into a Gen cluster. -
References
[1] Wang J, Han J G. The growth behaviors of the Zn-doped different sized germanium clusters: a density functional investigation. Chem Phys, 2007, 342: 253 doi: 10.1016/j.chemphys.2007.10.008[2] Mahtout S, Tariket Y. Electronic and magnetic properties of CrGen (15⩽ n ⩽ 29) clusters: a DFT study. Chem Phys, 2016, 472: 270 doi: 10.1016/j.chemphys.2016.03.011[3] Schmude R W, Gingerich K A. Thermodynamic study of small silicon carbide clusters with a mass spectrometer. J Phys Chem A, 1997, 101: 2610 doi: 10.1021/jp964093b[4] Samanta P N, Das K K. Electronic structure, bonding, and properties of SnmGen (m + n ⩽ 5) clusters: a DFT study. Comput Theor Chem, 2012, 980: 123 doi: 10.1016/j.comptc.2011.11.038[5] Kingcade J Jr, Gingerich K. Knudsen effusion mass spectrometric investigation of palladium-germanium clusters. Inorg Chem, 1989, 28: 89 doi: 10.1021/ic00300a020[6] Yadav P S, Yadav R K. Ab initio study of the physical properties of binary SimCn (m + n ⩽ 5) nanoclusters. J Phys Cond Matter, 2006, 18: 7085. doi: 10.1088/0953-8984/18/31/004[7] Bandyopadhyay D, Kumar M. The electronic structures and properties of transition metal-doped silicon nanoclusters: a density functional investigation. Chem Phys, 2008, 353: 170. doi: 10.1016/j.chemphys.2008.08.017[8] Han J G, Hagelberg F. Recent progress in the computational study of silicon and germanium clusters with transition metal impurities. J Comput Theor Nanosci, 2009, 6: 257 doi: 10.1166/jctn.2009.1035[9] Bals S, Van Aert S, Romero C P, et al. Atomic scale dynamics of ultrasmall germanium clusters. Nat Commun, 2012, 3: 897. doi: 10.1038/ncomms1887[10] Siouani C, Mahtout S, Safer S, et al. Structure, stability, and electronic and magnetic properties of VGen (n = 1–19) clusters. J Phys Chem A, 2017, 121, 3540 doi: 10.1021/acs.jpca.7b00881[11] Brack M. The physics of simple metal clusters: self-consistent jellium model and semiclassical approaches. Rev Mod Phys, 1993, 65: 677. doi: 10.1103/RevModPhys.65.677[12] Han J G, Zhang P F, Lic Q X, et al. A theoretical investigation of GenSn (n = 1–4) clusters. J Mol Struct, 2003, 624: 257 doi: 10.1016/S0166-1280(02)00790-X[13] Singh A K, Kumar V, Kawazoe, Y. Thorium encapsulated caged clusters of germanium: The Gen, n = 16, 18, and 20. J Phys Chem B, 2005, 109: 15187 doi: 10.1021/jp053169d[14] Wang J, Han J G. A computational investigation of copper-doped germanium and germanium clusters by the density-functional theory. J Chem Phys, 2005, 123: 244303. doi: 10.1063/1.2148949[15] Zhao W J, Wang, Y X. Geometries, stabilities, and magnetic properties of MnGen (n = 2–16) clusters: density-functional theory investigations. J Mol Struct, 2009, 901: 18 doi: 10.1016/j.theochem.2008.12.039[16] Jaiswal S, Kumar V. Growth behavior and electronic structure of neutral and anion ZrGen (n = 1–21) clusters. Comput Theor Chem, 2016, 1075: 87 doi: 10.1016/j.comptc.2015.11.013[17] Mahtout S, Siouani C, Rabilloud F. Growth behavior and electronic structure of noble metal-doped germanium clusters. J Phys Chem A, 2018, 122: 662 doi: 10.1021/acs.jpca.7b09887[18] Djaadi S, Aiadi K E, Mahtout S. First principles study of structural, electronic and magnetic properties of SnGen (0, ± 1)(n = 1–17) clusters. J Semicond, 2018, 39: 042001. doi: 10.1088/1674-4926/39/4/042001[19] Ordejón P, Artacho E, Soler J M. Self-consistent order-N density-functional calculations for very large systems. Phys Rev B, 1996, 53: R10441. doi: 10.1103/PhysRevB.53.R10441[20] Soler J M, Artacho E, Gale J D, et al. The siesta method for ab initio order-n materials simulation. J Phys Cond Matter, 2002, 14: 2745. doi: 10.1088/0953-8984/14/11/302[21] Troullier N, Martins J L. Efficient pseudopotentials for plane-wave calculations. Phys Rev B, 1991, 43: 1993. doi: 10.1103/PhysRevB.43.1993[22] Perdew J P, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B, 1981, 23: 5048. doi: 10.1103/PhysRevB.23.5048[23] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77: 3865. doi: 10.1103/PhysRevLett.77.3865[24] Bandyopadhyay D, Sen P. Density functional investigation of structure and stability of Gen and GenNi (n = 1–20) clusters: validity of the electron counting Rule. J Phys Chem A, 2010, 114: 1835 doi: 10.1021/jp905561n[25] Shi S, Liu Y, Zhang C, et al. A computational investigation of aluminum-doped germanium clusters by density functional theory study. Comput Theor Chem, 2015, 1054: 8 doi: 10.1016/j.comptc.2014.12.004[26] Kapila N, Garg I, Jindal V K, et al. First principle investigation into structural growth and magnetic properties in GenCr clusters for n = 1–13. J Mag Mag Mater, 2012. 324: 2885 doi: 10.1016/j.jmmm.2012.04.042[27] Wang J, Wang G, Zhao J. Structure and electronic properties of Gen (n = 2–25) clusters from density-functional theory. Phys Rev B, 2001, 64: 205411. doi: 10.1103/PhysRevB.64.205411[28] Yoshida M, Aihara J I. Validity of the weighted HOMO-LUMO energy separation as an index of kinetic stability for fullerenes with up to 120 carbon atoms. Phys Chem Chem Phys, 1999, 1: 227 doi: 10.1039/a807917j[29] Parr R G, Pearson R G. Absolute hardness: companion parameter to absolute electronegativity. J Am Chem Soc, 1983, 105, 7512 doi: 10.1021/ja00364a005[30] Sosa-Hernández E, Alvarado-Leyva P. Magnetic properties of stable structures of small binary FenGem (n + m ⩽ 4) clusters. Physica E, 2009, 42: 17 doi: 10.1016/j.physe.2009.07.013[31] Li X, Su K, Yang X, et al. Size-selective effects in the geometry and electronic property of bimetallic Au-Ge nanoclusters. Comput Theor Chem, 2013, 1010: 32 doi: 10.1016/j.comptc.2013.01.012[32] Kingcade J E, Nagarathna-Naik H M, Shim I, et al. Electronic structure and bonding of the dimeric germanium molecule from all-electron ab initio calculations and equilibrium measurements. J Phys Chem, 1986, 90: 2830 doi: 10.1021/j100404a011[33] Nagendran S, Sen S S, Roesky H W, et al. RGe(I)Ge(I)R Compound (R = PhC(NtBu)2) with a Ge−Ge single bond and a comparison with the gauche conformation of hydrazine. Organometallics, 2008, 27: 5459 doi: 10.1021/om800714f[34] Gadiyak G V, Morokov Y. N, Mukhachev A G, et al. Electron density functional method for molecular system calculations. J Struct Chem, 1982, 22: 670 doi: 10.1007/BF00746425[35] Wang J, Han J G. Geometries, stabilities, and vibrational properties of bimetallic Mo2-doped Gen (n = 9–15) clusters: a density functional investigation. J Phys Chem A, 2008, 112: 3224 doi: 10.1021/jp710238t[36] Kant A, Strauss B H. Atomization energies of the polymers of germanium, Ge2 to Ge7. J Chem Phys, 1966. 45: 822 doi: 10.1063/1.1727688[37] Vasiliev I S, Öğüt S, Chelikowsky J R. Ab initio calculations for the polarizabilities of small semiconductor clusters. Phys Rev Lett, 1997, 78: 4805. doi: 10.1103/PhysRevLett.78.4805[38] Burton G R, Xu C, Arnold C C, et al. Photoelectron spectroscopy and zero electron kinetic energy spectroscopy of germanium cluster anions. J Chem Phys, 1996, 104: 2757 doi: 10.1063/1.471098[39] Safer S, Mahtout S, Rezouali K, et al. Properties of neutral and charged cobalt-doped arsenic CoAsn (0 ± 1) (n = 1–15) clusters by density functional theory. Comput Theor Chem, 2016, 1090: 23 doi: 10.1016/j.comptc.2016.05.016[40] Guo L. The structure and energetic of AlAsn (n = 1–15) clusters: a first-principles study. J Alloys Compounds, 2010, 498: 121 doi: 10.1016/j.jallcom.2010.02.202[41] Pearson R G. Chemical hardness: applications from molecules to solids. Weinheim: Wiley-VCH, 1997 -
Proportional views






 DownLoad:
DownLoad: