| Citation: |
Linwang Wang. Some recent advances in ab initio calculations of nonradiative decay rates of point defects in semiconductors[J]. Journal of Semiconductors, 2019, 40(9): 091101. doi: 10.1088/1674-4926/40/9/091101
****
L W Wang, Some recent advances in ab initio calculations of nonradiative decay rates of point defects in semiconductors[J]. J. Semicond., 2019, 40(9): 091101. doi: 10.1088/1674-4926/40/9/091101.
|
Some recent advances in ab initio calculations of nonradiative decay rates of point defects in semiconductors
DOI: 10.1088/1674-4926/40/9/091101
More Information
-
Abstract
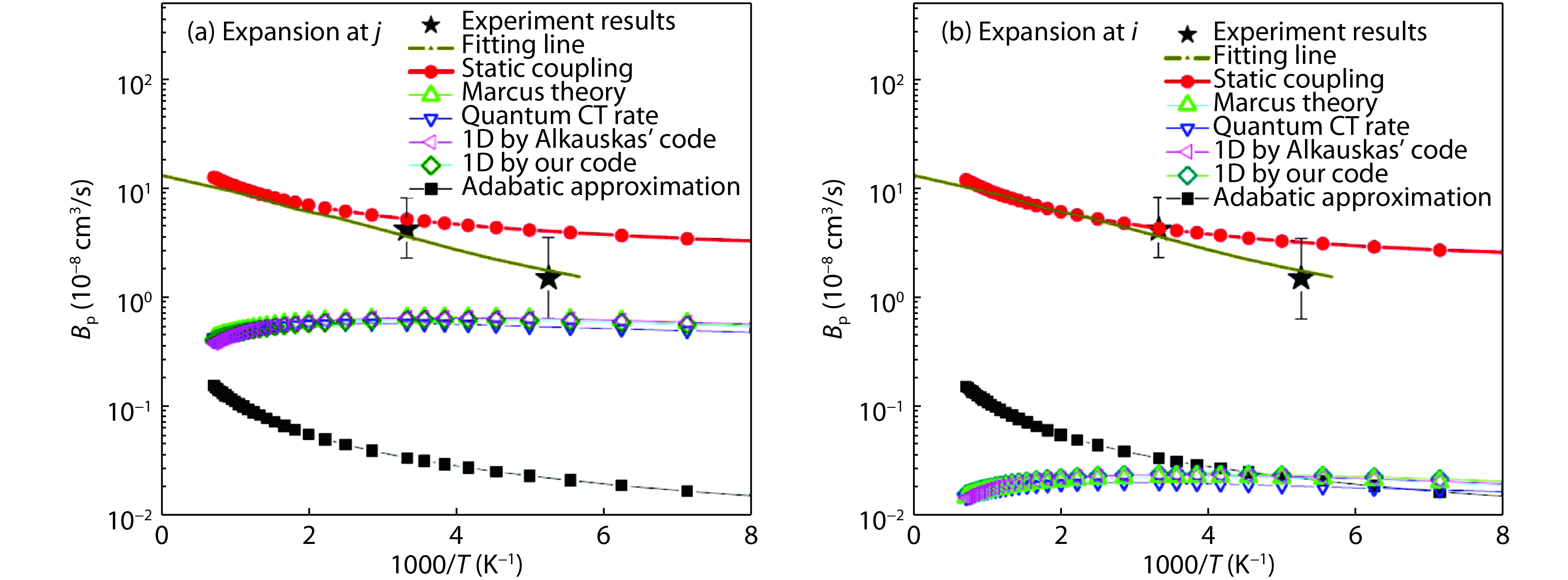
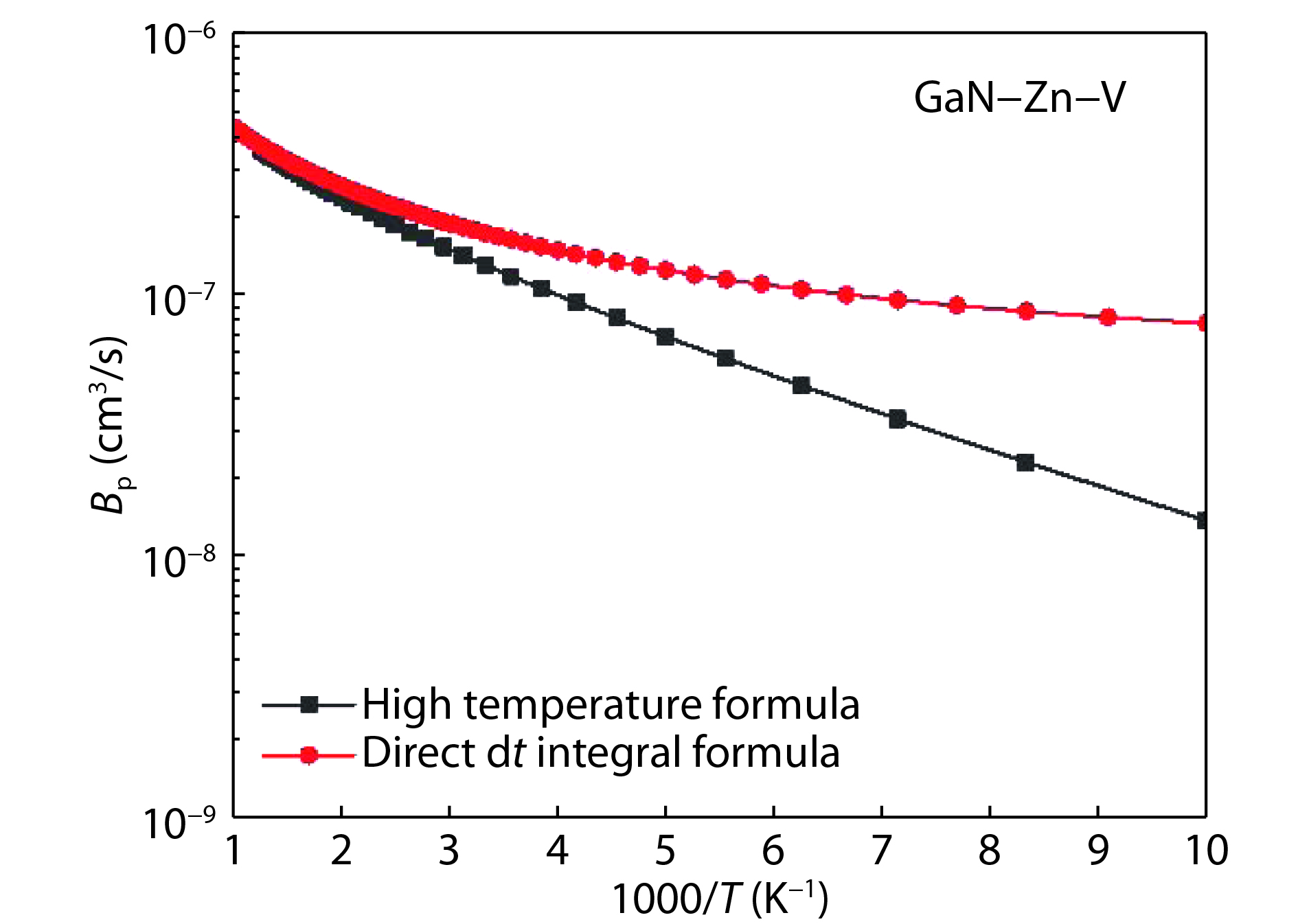
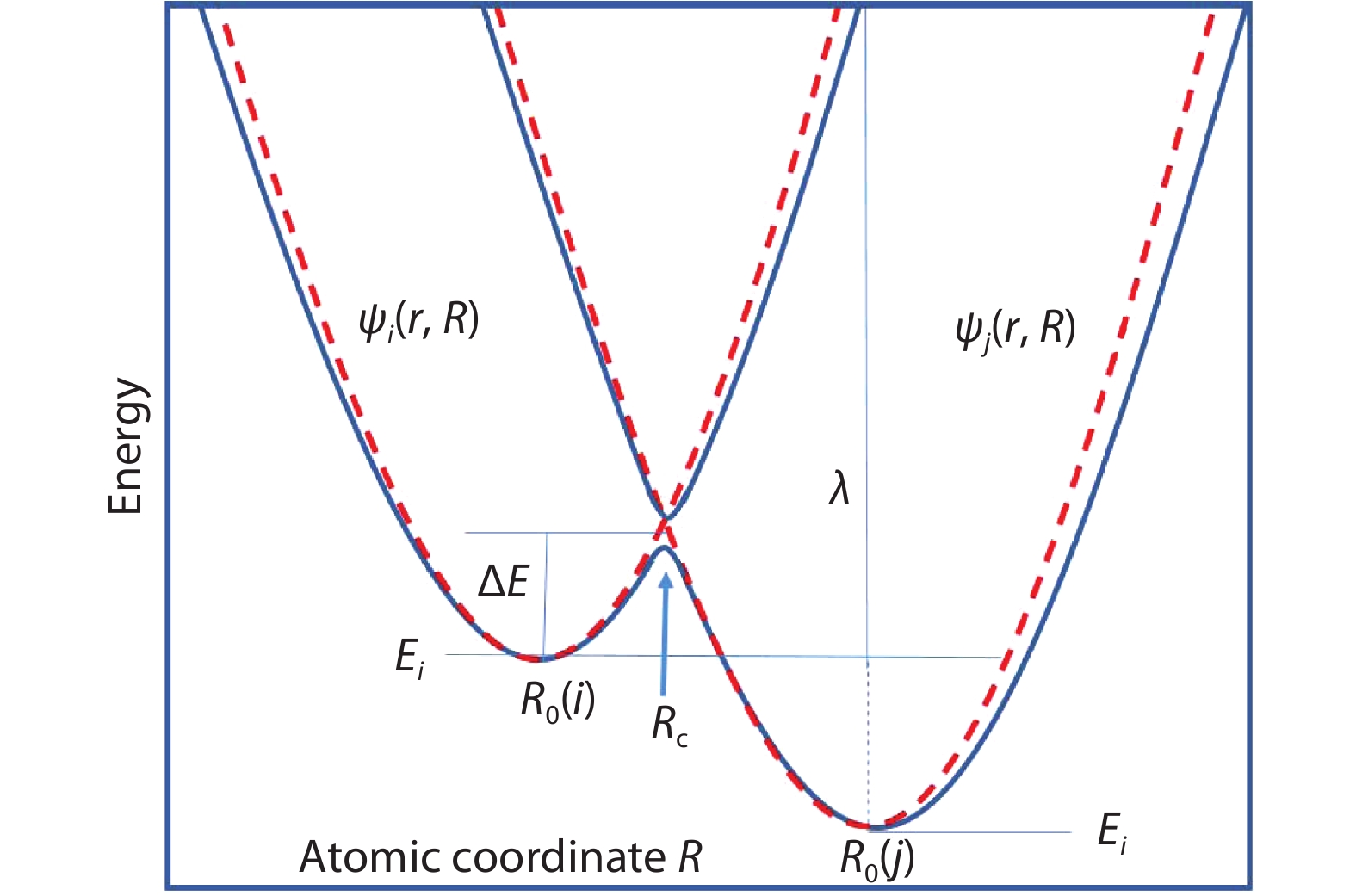
In this short review, we discuss a few recent advances in calculating the nonradiative decay rates for point defects in semiconductors. We briefly review the debates and connections of using different formalisms to calculate the multi-phonon processes. We connect Dr. Huang’s formula with Marcus theory formula in the high temperature limit, and point out that Huang’s formula provide an analytical expression for the phonon induced electron coupling constant in the Marcus theory formula. We also discussed the validity of 1D formula in dealing with the electron transition processes, and practical ways to correct the anharmonic effects. -
References
[1] Peka S I. Theory of F-centers. Zh Eksp Theor Fiz, 1950, 20, 510[2] Huang K. Theory of light absorption and non-radiative transitions in F-centres. Phys Proc Roy Soc A, 1950, 204(22), 406 doi: 10.1098/rspa.1950.0184[3] Kovaskiy V A. Theory of nonradiative transitions in noncondon approximation: Low temperatures. Phys Solid State, 1962, 4, 1635[4] Kovarskiy V A, Tchaikovskiy I A, Sinyavskiy E P. Quantum kinetic equations for processes with nonradiative recombination. Phys Solid State, 1964, 8, 2129[5] Passler R. Description of nonradiative multiphonon transitions in the static coupling scheme. Czecho J Phys, 1974, 24(3), 322 doi: 10.1007/BF01596354[6] Passler R. Description of nonradiative multiphonon transitions in the static coupling scheme II. Approximations. Czecho J Phys, 1975, 25, 219 doi: 10.1007/BF01589478[7] Freed K F, Jortner J. Multiphonon processes in the nonradiative decay of large molecules. J Chem Phys, 1970, 52, 6272 doi: 10.1063/1.1672938[8] Huang K. Adiabatic approximation theory and static coupling theory of nonradiative transitons. Scientia Sinica, 1981, 24, 27[9] Huang K. Lattice relaxation and theory of multiphonon transitions. Prog Phys, 1981, 1, 31 doi: 10.1080/00107518108231558[10] Landau L, Litshitz E M. Quantum mechanics: Nonrelativistic theory. New York: Pergamon, 1977[11] Zener C. Non-adiabatic crossing of energy levels. Proc Roy Soc A, 1932, 137, 696[12] Marcus R A. Electron transfer reactions in chemistry. Theory and experiment. Rev Mod Phys, 1993, 65, 599 doi: 10.1103/RevModPhys.65.599[13] Henry C H, Lang D V. Nonradiative capture and recombination by multiphonon emission in GaAs and GaP. Phys Rev B, 1977, 15, 989 doi: 10.1103/PhysRevB.15.989[14] Alkauskas A, Yan Q, Van de Walle C G. First-principles theory of nonradiative carrier capture via multiphonon emission. Phys Rev B, 2014, 90, 075202 doi: 10.1103/PhysRevB.90.075202[15] Shi L, Wang L W. Ab initio calculations of deep-level carrier nonradiative recombination rates in bulk semiconductors. Phys Rev Lett, 2012, 109, 245501 doi: 10.1103/PhysRevLett.109.245501[16] Shi L, Xu K, Wang L W. Reply to " Comment on ‘Comparative study of ab initio nonradiative recombination rate calculations under different formalisms’ ”. Phys Rev B, 2018, 97, 077302 doi: 10.1103/PhysRevB.97.077302[17] Liu Y Y, Zheng F, Jiang X, et al. Ab initio investigation of charge trapping across the crystalline–Si–amorphous–SiO2 interface. Phys Rev Appl, 2019, 11, 044058 doi: 10.1103/PhysRevApplied.11.044058[18] Nalbach P, Thorwart M. Landau-Zener transitions in a dissipative environment: numerically exact results. Phys Rev Lett, 2009, 103, 220401 doi: 10.1103/PhysRevLett.103.220401[19] Zhang S S, Gao W, Cheng H, et al. Symmetry-breaking assisted Landau-Zener transitions in Rydberg atoms. Phys Rev Lett, 2018, 120, 063203 doi: 10.1103/PhysRevLett.120.063203[20] Wei S W. Overcoming the doping bottleneck in semiconductors. Comput Mater Sci, 2004, 30, 337 doi: 10.1016/j.commatsci.2004.02.024[21] Lany S, Zunger A. Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs. Phys Rev B, 2008, 78, 235104 doi: 10.1103/PhysRevB.78.235104[22] Freysoldt C, Grabowski B, Hickel T, et al. First-principles calculations for point defects in solids. Rev Mod Phys, 2014, 86, 253 doi: 10.1103/RevModPhys.86.253[23] Heyd J, Scuseria G E, Ernerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys, 2003, 118, 8207 doi: 10.1063/1.1564060[24] Lyons J L, Van de Walle C G. Computationally predicted energies and properties of defects in GaN. npj Comput Mat, 2017, 3, 12 doi: 10.1038/s41524-017-0014-2[25] Shuai Z, Wang L, Song C. Theory of charge transport in carbon electronic materials. Springer Science & Business Media, 2012[26] Ferrer F J A, Cerezo J, Soto J, et al. First-principle computation of absorption and fluorescence spectra in solution accounting for vibronic structure, temperature effects and solvent inhomogenous broadening. Comput Theor Chem, 2014, 1040, 328 doi: 10.1016/j.comptc.2014.03.003[27] Baiardi A, Bloino J, Barone V. General time dependent approach to vibronic spectroscopy including Franck–Condon, Herzberg–Teller, and Duschinsky effects. J Chem Theory Comput, 2013, 9, 4097 doi: 10.1021/ct400450k[28] Borrelli R, Capobianco A, Peluso A. Generating function approach to the calculation of spectral band shapes of free-base Chlorin including Duschinsky and Herzberg-Teller effects. J Phys Chem A, 2012, 116, 9934 doi: 10.1021/jp307887s[29] Lin S H. Rate of interconversion of electronic and vibrational energy. J Chem Phys, 1966, 44, 3759 doi: 10.1063/1.1726531[30] http://www.pwmat.com[31] Shi L, Xu K, Wang L W. Comparative study of ab initio nonradiative recombination rate calculations under different formalisms. Phys Rev B, 2015, 91, 205315 doi: 10.1103/PhysRevB.91.205315[32] Aratat Y, Mohammedy F M, Hassan M M S. Optical and other measurement techniques of carrier lifetime in semiconductors. Int J Optoelectron Eng, 2012, 2, 5 doi: 10.5923/j.ijoe.20120202.02[33] Kim S, Hood S N, Wash A. Anharmonic lattice relaxation during nonradiative carrier capture. Phys Rev B, 2019, 100, 041202 doi: 10.1103/PhysRevB.100.041202[34] Yang J H, Shi L, Wang L W, et al. Non-radiative carrier recombination enhanced by two-level process: a first-principles study . Sci Rep, 2016, 6, 21712 doi: 10.1038/srep21712[35] Wang Z, Li S S, Wang L W. Efficient real-time time-dependent density functional theory method and its application to a collision of an ion with a 2D material. Phys Rev Lett, 2015, 114, 063004 doi: 10.1103/PhysRevLett.114.063004[36] Kang J, Wang L W. Nonadiabatic molecular dynamics with decoherence and detailed balance under a density matrix ensemble formalism. Phys Rev B, 2019, 99, 224303 doi: 10.1103/PhysRevB.99.224303 -
Proportional views





 DownLoad:
DownLoad: