| Citation: |
T. Bendib, F. Djeffal, D. Arar. A compact charge-based model to study the nanoscale undoped double gate MOSFETs for nanoelectronic circuit design using genetic algorithms[J]. Journal of Semiconductors, 2013, 34(4): 044003. doi: 10.1088/1674-4926/34/4/044003
****
T. Bendib, F. Djeffal, D. Arar. A compact charge-based model to study the nanoscale undoped double gate MOSFETs for nanoelectronic circuit design using genetic algorithms[J]. J. Semicond., 2013, 34(4): 044003. doi: 10.1088/1674-4926/34/4/044003.
|
A compact charge-based model to study the nanoscale undoped double gate MOSFETs for nanoelectronic circuit design using genetic algorithms
DOI: 10.1088/1674-4926/34/4/044003
More Information
-
Abstract
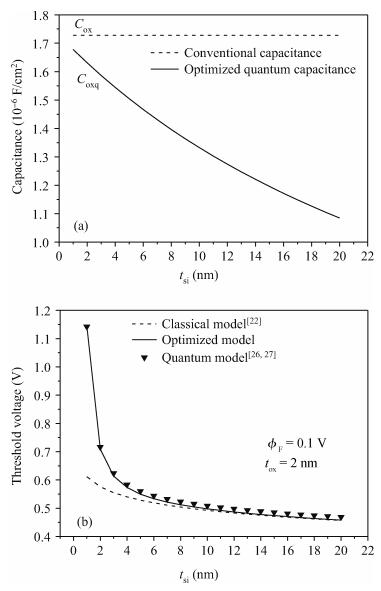
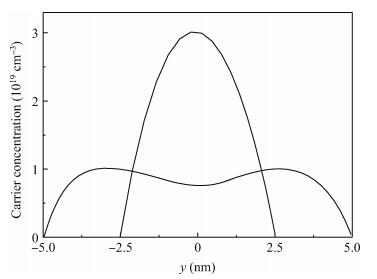
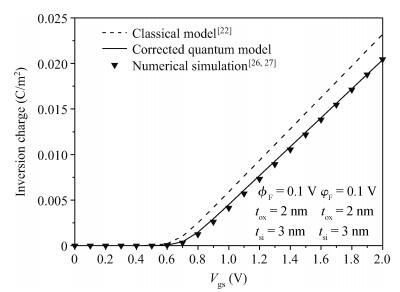
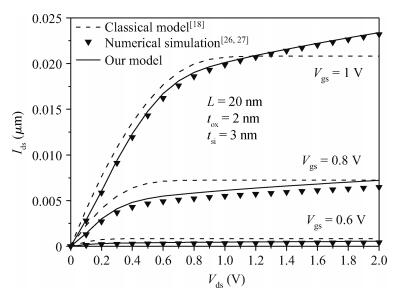
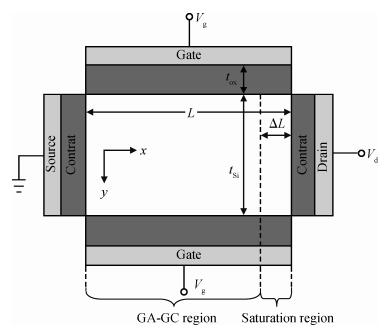
The analytical modeling of nanoscale devices is an important area of computer-aided design for fast and accurate nanoelectronic design and optimization. In the present paper, a new approach for modeling semiconductor devices, nanoscale double gate DG MOSFETs, by use of the gradual channel approximation (GC) approach and genetic algorithm optimization technique (GA) is presented. The proposed approach combines the universal optimization and fitting capability of GA and the cost-effective optimization concept of quantum correction, to achieve reliable, accurate and simple compact models for nanoelectronic circuit simulations. Our compact models give good predictions of the quantum capacitance, threshold voltage shift, quantum inversion charge density and drain current. These models have been verified with 2D self-consistent results from numerical calculations of the coupled Poisson-Schrödinger equations. The developed models can also be incorporated into nanoelectronic circuit simulators to study the nanoscale CMOS-based devices without impact on the computational time and data storage.-
Keywords:
- nanoscale,
- quantum,
- genetic algorithm,
- analytical model
-
References
[1] The International Technology Roadmap for Semiconductors, 2007. Online Available: http//public.itrs.net[2] Djeffal F, Ghoggali Z, Dibi Z, et al. Analytical analysis of nanoscale multiple gate MOSFETs including effects of hot-carrier induced interface charges. Microelectron Reliab, 2009, 49:337[3] Djeffal F, Chahdi M, Benhaya A, et al. An approach based on neural computation to simulate the nanoscale CMOS circuits:ap-plication to the simulation of CMOS inverter. Solid-State Elec-tron, 2007, 51:48 doi: 10.1016/j.sse.2006.12.004[4] Stern F. Self-consistent results for n-type Si inversion layers. Phys Rev B, 1972, 5:4891 doi: 10.1103/PhysRevB.5.4891[5] Baccarani G, Reggiani S. A compact double-gate MOSFET model comprising quantum-mechanical and nonstatic effects. IEEE Trans Electron Devices, 1999, 46:1656 doi: 10.1109/16.777154[6] Chen Q, Meindl J D. Nanoscale metal oxide semiconductor field effect transistors:scaling limits and opportunities. Nanotechnology, 2004, 15:8549[7] Lopez-Villanueva J A, Cartujo-Cassinello P, Gamiz F, et al. Effects of the inversion layer centroid on the performance of DG MOSFETs. IEEE Trans Electron Devices, 2000, 47:141 doi: 10.1109/16.817579[8] Hariharan V, Thakker R, Singh K, et al. Drain current model for nanoscale double-gate MOSFETs. Solid-State Electron, 2009, 53:1001 doi: 10.1016/j.sse.2009.05.008[9] Djeffal F, Abdi M A, Dibi Z, et al. A neural approach to study the scaling capability of the undoped double-gate and cylindrical gate all around MOSFETs. Mater Sci & Eng B, 2007, 27:1111[10] Reyboz M, Rozeau O, Poiroux T, et al. An explicit analytical charge-based model of undoped independent double gate MOSFET. Solid-State Electron, 2006, 50:1276 doi: 10.1016/j.sse.2006.05.019[11] Lazaro A, ANe B, Moldovan O, et al. A compact quantum model of nanoscale double-gate metal-oxide-semiconductor field-effect transistor for high frequency and noise simulations. J Appl Phys, 2006, 100:084320 doi: 10.1063/1.2360379[12] Nae B, Lazaro A, Iñiguez B. High frequency and noise model of gate-all-around metal-oxide-semiconductor field-effect transistors. J Appl Phys, 2009, 105:074505 doi: 10.1063/1.3093884[13] Bentrcia T, Djeffal F, Benhaya A. Continuous analytic Ⅰ-Ⅴ model for GS DG MOSFETs including hot-carrier degradation effects. Journal of Semiconductors, 2012, 33:014001: doi: 10.1088/1674-4926/33/1/014001[14] Goldberg D E. Genetic algorithms in search, optimization, and machine learning reading. MA:Addison-Wesley, 1989[15] Painton L, Campbell J. Genetic algorithms in optimization of system reliability. IEEE Trans Reliab, 1995, 44:172 doi: 10.1109/24.387368[16] Iñiguez B, Fjeldly T A, Lázaro A, et al. Compact-modeling solutions for nanoscale double-gate and gate-all-around MOSFETs. IEEE Trans Electron Devices, 2006, 53:2128 doi: 10.1109/TED.2006.881007[17] Xiong S, King T J, Bokor J. A comparison study of symmetric ultrathin body double gate devices with metal source/drain and doped source/drain. IEEE Trans Electron Devices, 2005, 52:1859 doi: 10.1109/TED.2005.852893[18] Taur Y, Liang X, Wang W, et al. A continuous analytic drain current model for double gate MOSFETs. IEEE Electron Device Lett, 2004, 25:107 doi: 10.1109/LED.2003.822661[19] Datta S, Assad F, Lundstrom M S. The Si MOSFET from a transmission viewpoint. Superlattices and Microstructures, 1998, 23:771 doi: 10.1006/spmi.1997.0563[20] Naveh Y, Likharev K K. Shrinking limits of silicon MOSFETs:numerical study of 10 nm scale devices. Superlattices and Microstructures, 2000, 27:111 doi: 10.1006/spmi.1999.0807[21] Chen Q, Harrell E M, Meindl J D. A physical short-channel threshold voltage model for undoped symmetric double-gate MOSFETs. IEEE Trans Electron Devices, 2003, 50:1631 doi: 10.1109/TED.2003.813906[22] Taur Y. Analytic solutions of charge and capacitance in symmetric and asymmetric double-gate MOSFETs. IEEE Trans Electron Devices, 2001, 48:2861 doi: 10.1109/16.974719[23] Reggiani S, Gnani E, Gnudi A, et al. Low-field electron mobility model for ultrathin-body SOI and double-gate MOSFETs with extremely small silicon thickness. IEEE Trans Electron Devices, 2007, 54:2204 doi: 10.1109/TED.2007.902899[24] Munteanu D, Autran J L, Loussier X, et al. Quantum short-channel compact modelling of drain-current in double-gate MOSFET. Solid-State Electron, 2006, 50:680 doi: 10.1016/j.sse.2006.03.038[25] Lime F, Iñiguez B, Moldovan O. A quasi two-dimensional compact drain current model for undoped symmetric double gate MOSFETs including short-channel effects. IEEE Trans Electron Devices, 2008, 55:1441 doi: 10.1109/TED.2008.921980[26] ATLAS: 2D Device Simulator, SILVACO International, 2008[27] Ren Z, Venugopal R, Goasguen S, et al. NanoMOS2.5:a two-dimensional simulator for quantum transport in double-gate MOSFETs. IEEE Trans Electron Devices, 2003, 50:1914 doi: 10.1109/TED.2003.816524 -
Proportional views





 DownLoad:
DownLoad: