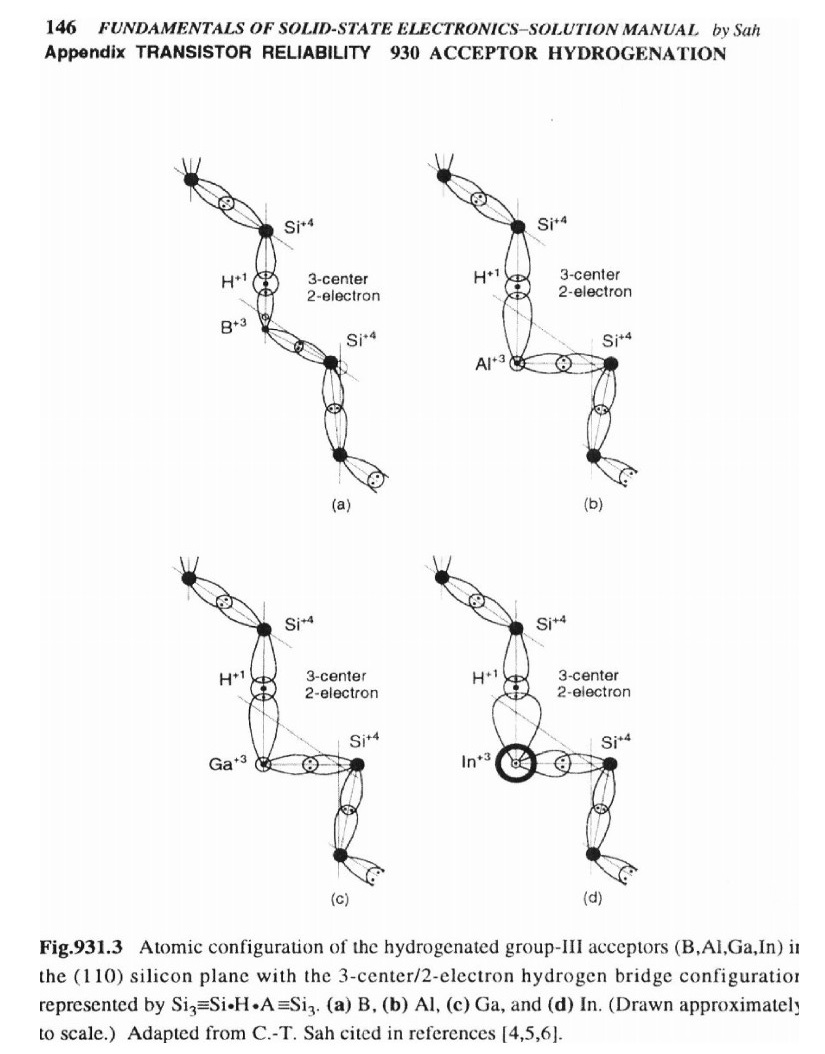
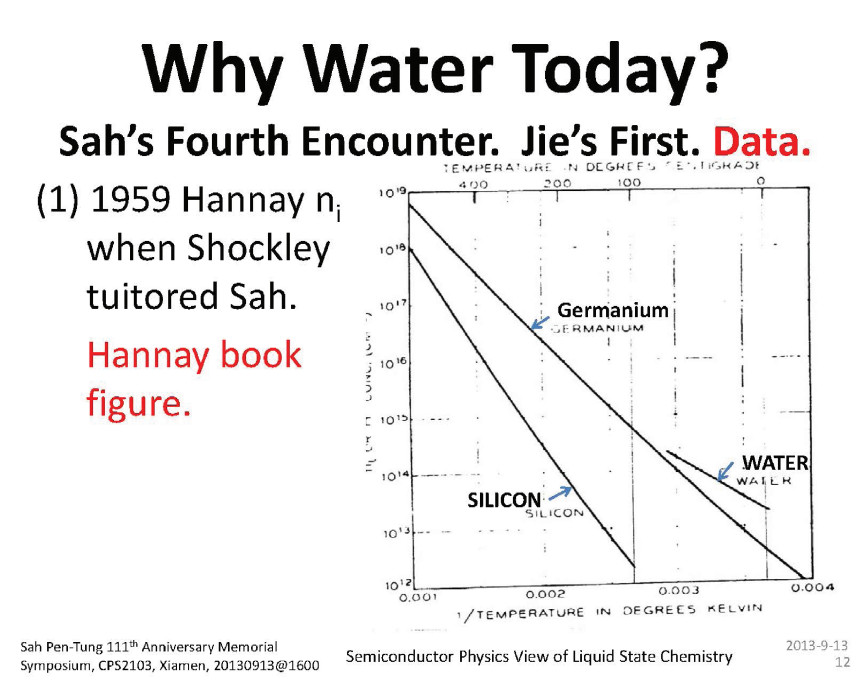
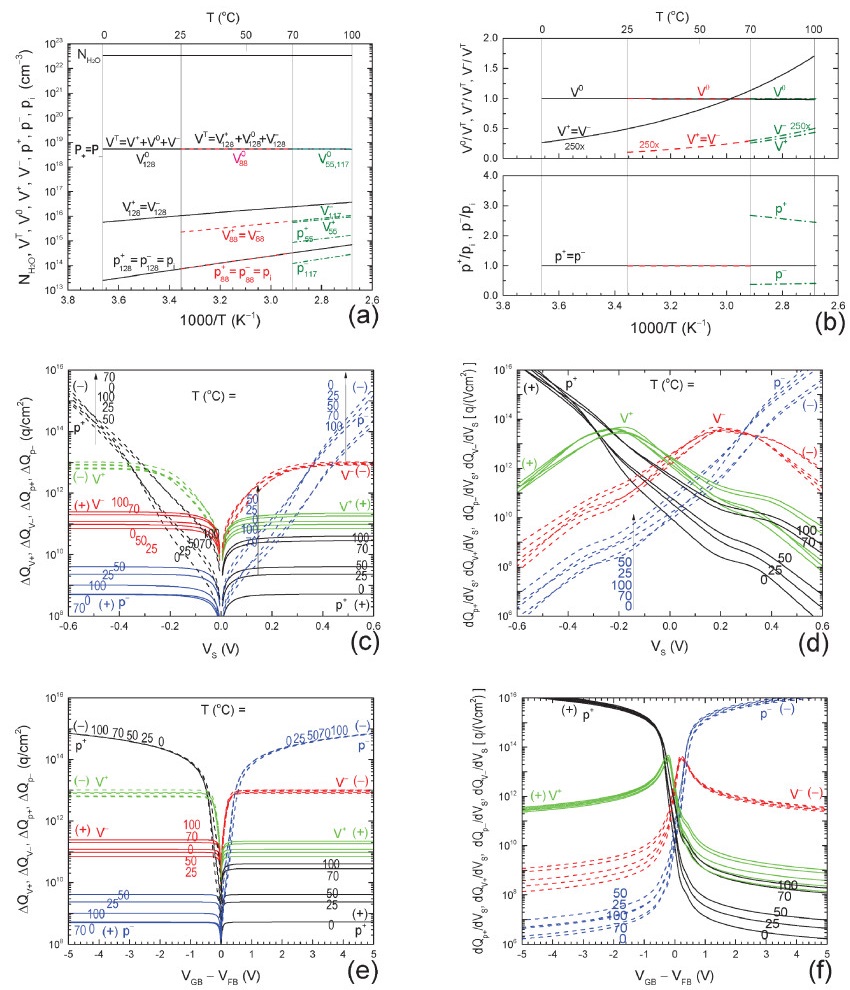
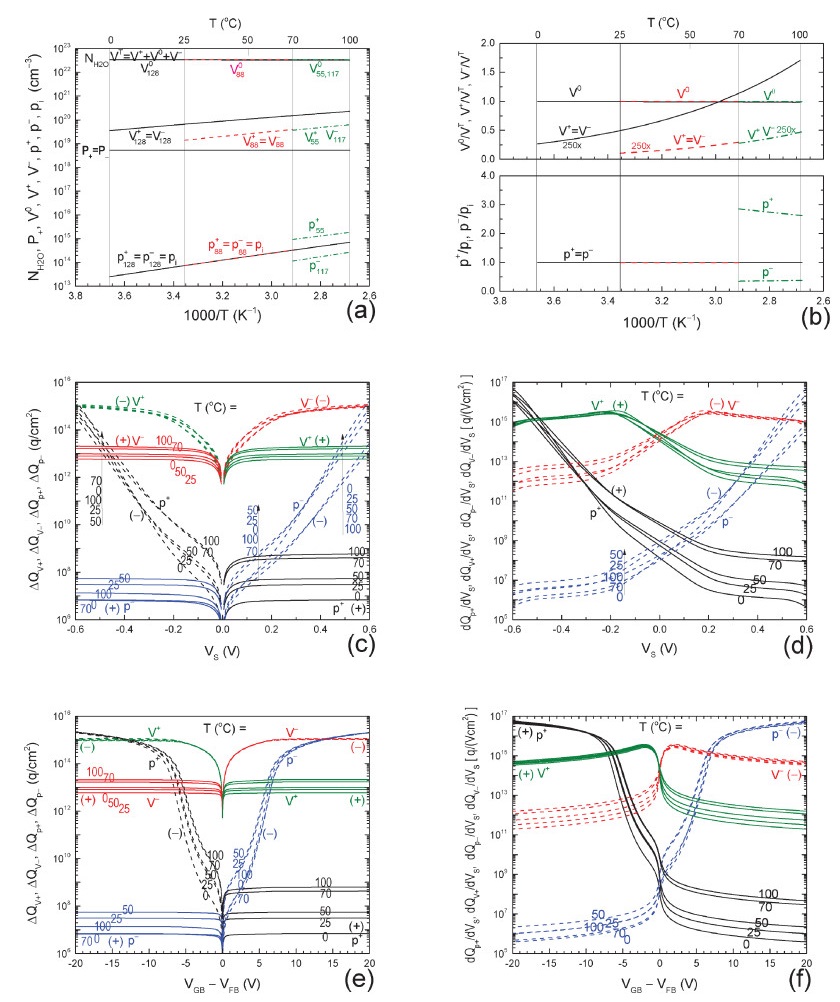
| Citation: |
Binbin Jie, Chihtang Sah. Solid State Physics View of Liquid State Chemistry Ⅲ. Electrical Conductance of Pure and Impure Water[J]. Journal of Semiconductors, 2014, 35(4): 041001. doi: 10.1088/1674-4926/35/4/041001
****
B B Jie, C T Sah. Solid State Physics View of Liquid State Chemistry Ⅲ. Electrical Conductance of Pure and Impure Water. J. Semicond., 2014, 35(4): 041001. doi: 10.1088/1674-4926/35/4/041001.
|
Solid State Physics View of Liquid State Chemistry Ⅲ. Electrical Conductance of Pure and Impure Water
DOI: 10.1088/1674-4926/35/4/041001
More Information
-
Abstract
The ‘abnormally’ high electrical conductivity of pure water was recently studied by us using our protonic bond, trap and energy band model, with five host particles:the positive and negative protons, and the amphoteric protonic trap in three charge states, positive, neutral and negative.Our second report described the electrical charge storage capacitance of pure and impure water.This third report presents the theory of particle density and electrical conductance of pure and impure water, including the impuritons, which consist of an impurity ion bonded to a proton, proton-hole or proton trap and which significantly affect impure waters' properties. -
References
[1] Jie Binbin and Sah Chihtang, "Solid State Physics View of Liquid State Chemistry-Electrical Conduction in Pure Water, " Journal of Semiconductors 34(12) 121001-8, December 2013. (Xiamen University, China. ) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bdtx201402001&dbname=CJFD&dbcode=CJFQ[2] Jie Binbin and Sah Chihtang, "Solid State Physics View of Liquid State Chemistry-Ⅱ. Electrical Capacitance of Pure and Impure Water, " Journal of Semiconductors 35(2) 021001-19, February 2014. (Xiamen University, China. )[3] Sah Chihtang and Jie Binbin, "Semiconductor Physics View of Liquid State Chemistry, " Invited Paper at the Special Session, the Sah Pen-Tung 111th Anniversary Symposium, of the 2013 National Fall-Meeting of the Chinese Physical Society, September 13-15, 2013, Xiamen University, Xiamen, Fujian, China. Future presentations to give prompt report of progress and to get feedbacks were tentatively accepted by us, as invited keynotes at two international conferences: IEEE-ISNE at Tao-Yuan, Taiwan on 20140507 and WCM2014 in Washington DC on 20140616. Additional presentations may be scheduled during these periods.[4] Linus Pauling, "The structure and entropy of ice and other crystals with some randomness of atomic arrangement, " J. Amer. Chem. Soc. 57(12), 2680-2684, December 1935. Received September 24, 1935. (Gates Chemical Laboratory, Caltech, Pasadena. ) doi: 10.1021/ja01315a102[5] J. D. Bernal and R. H. Fowler, "A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions, " J. Chem. Phys. 1(8), 515-548, August, 1933. Received April 29, 1933. (University of Cambridge, England. )[6] W. F. Giauque and H. L. Johnston, "Symmetrical and Antisymmetrical Hydrogen and the Third Law of Thermodynamics. Thermal Equilibrium and the Triple Point Pressure, " J. Amer. Chem. Soc. 50, 3221-3228, 1928; J. O. Clayton and W. F. Giauque, "The Heat Capacity and Entropy of Carbon Monoxide. Heat of Vaporation. Vapor Pressures of Solid and Liquid. Free Energy To 5000oK. From Spectroscopic Data, " J. Amer. Chem. Soc. 54, 2610-2626, 1932; W. W. Blue and W. F. Giauque, "The Heat Capacity and Vapor Pressure of Solid and Liquid Nitrous Oxide. The Entropy from its Band Spectrum, " J. Amer. Chem. Soc. 57, 991-997, 1935. (All at University of California at Berkeley). All here were quoted by Pauling in [4 ].[7] John C. Slater, Introduction to Chemical Physics, McGraw-Hill Book company, 1939; Dover edition, 1970. 521pp. See also his later Quantum Theory of Matter books on atoms, molecules and solids, which we cited in our first and second report[1 ,2 ].[8] William Shockley, Electrons and Holes in Semiconductors, D. Van-Nostrand Co, Inc. Original Edition 1950, 9th printing 1966, reprinted 1976 by Krieger Publishing Co. , Inc. Florida, USA. 561pp.[9] John M. Ziman, Models of Disorder-The theoretical physics of homogenously disordered system, Cambridge University Press, 1979. 525pp.[10] Tak H. Ning and Chih-Tang Sah, "Multivalley effective-mass approximation for donor states in silicon. I. Shallow-level group-V impurities, " Physical Review B, v4, 3468-3481, 15 November 1971; and "Multivalley effective-mass approximation for donor states in silicon. Ⅱ. Deep-level group-VI double-donor impurities, " Physical Review B, v4, 3482-3488, 15 November 1971.[11] Sokrates T. Pantelides and Chih-Tang Sah, "Theory of localized states in semiconductors. I. New results using an old method, " Physical Review B. v10, 621-637, 15 July 1974; and "Theory of localized states in semiconductors. Ⅱ. The pseudo impurity theory application to shallow and deep donors in silicon, " Physical Review B, v10, 638-658, 15 July 1974. http://adsabs.harvard.edu/abs/1974PhRvB..10..621P[12] Chih-Tang Sah and William Shockley, "Electron-hole recombination statistics in semiconductors through flaws with many charge conditions, " Physical Review, v109, 1103-1115, 15 February 1958. doi: 10.1103/PhysRev.109.1103[13] Chih-Tang Sah, "The equivalent circuit model in solid-state electronics, I. The single level defect centers, " Proc. IEEE, v55, 654-672, May 1967. "The equivalent circuit model in solid-state electronics, Ⅱ. The multiple level impurity centers, "Proc. IEEE, v55, 673-685, May 1967. "The equivalent circuit model in solid-state electronics, Ⅲ. Conduction and displacement currents, " SolidState Electronics, v13, 1547-1575, December 1970. "Equivalent circuit models in semiconductor transport for thermal, optical, Auger-impact and tunneling recombination-generation-trapping processes, " Physica Status Solidi, (a)v7, 541-559, 16 October 1971.[14] Jie Binbin and Sah Chihtang, "MOS Capacitance-Voltage Characteristics from Electron-Trapping at Dopant Donor Impurity, " Journal of Semiconductors, 32(4), 041001-1-9, April 2011. "MOS Capacitance-Voltage Characteristics: Ⅱ. Sensitivity of Electronic Trapping at Dopant Impurity from Parameter Variations, " Journal of Semiconductors, 32(12), 121001-1-11, December 2011. "MOS Capacitance-Voltage Characteristics: Ⅲ. Trapping Capacitance from 2-Charge-State Impurities, " Journal of Semiconductors, 32(12), 121002-1-16, December 2011. "MOS Capacitance-Voltage Characteristics: IV. Trapping Capacitance from 3-Charge-State Impurities, " Journal of Semiconductors, 33(1), 011001-1-19, January 2012. "MOS Capacitance-Voltage Characteristics: V. Methods to Enhance the Trapping Capacitance" Journal of Semiconductors, 33(2), 011001-1-19, February 2012.[15] William L. Marshall and E. U. Franck, "Ion Product of Water Substance, 0-1000C, 1-10000 bars-New International Formulation and Its Background, " J. Phys. Chem. Ref. Data, vol. 10, No. 2, pp. 295-304, 1981. -
Proportional views





.jpg)
 DownLoad:
DownLoad:
.jpg)