| Citation: |
Yuelin Wang, Tie Li, Xiao Zhang, Hongjiang Zeng, Qinhua Jin. In situ TEM/SEM electronic/mechanical characterization of nano material with MEMS chip[J]. Journal of Semiconductors, 2014, 35(8): 081001. doi: 10.1088/1674-4926/35/8/081001
****
Y L Wang, T Li, X Zhang, H J Zeng, Q H Jin. In situ TEM/SEM electronic/mechanical characterization of nano material with MEMS chip[J]. J. Semicond., 2014, 35(8): 081001. doi: 10.1088/1674-4926/35/8/081001.
|
In situ TEM/SEM electronic/mechanical characterization of nano material with MEMS chip
DOI: 10.1088/1674-4926/35/8/081001
More Information
-
Abstract
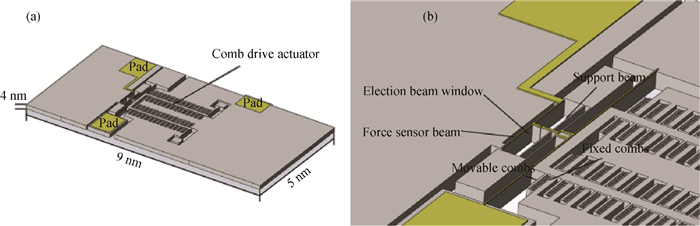
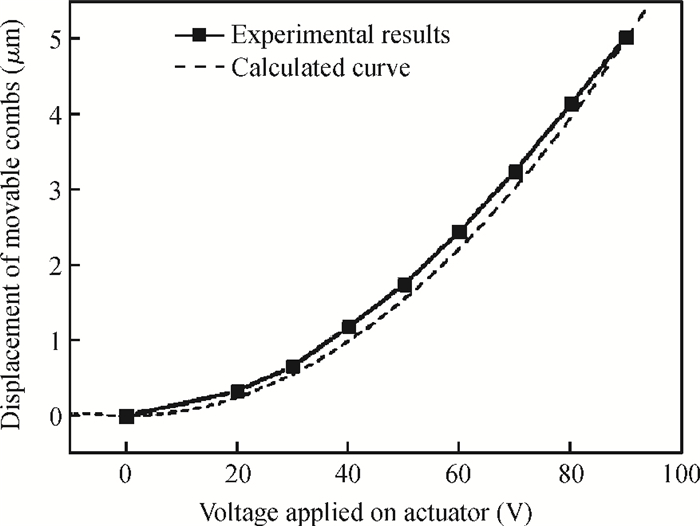
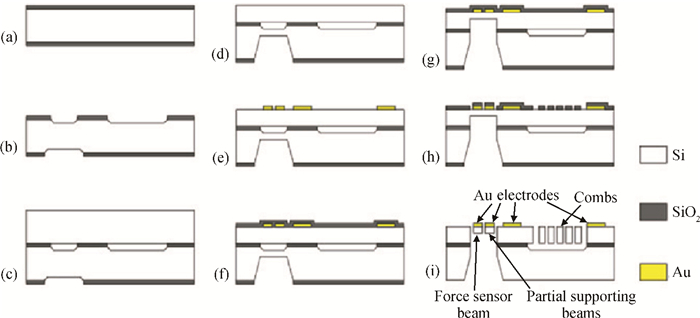
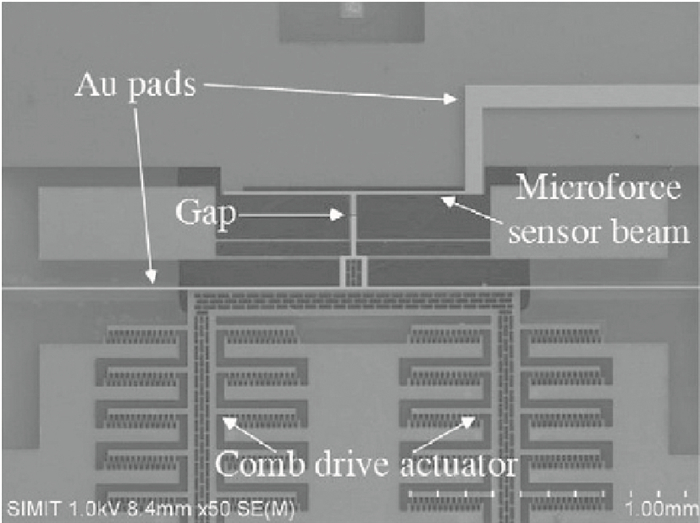
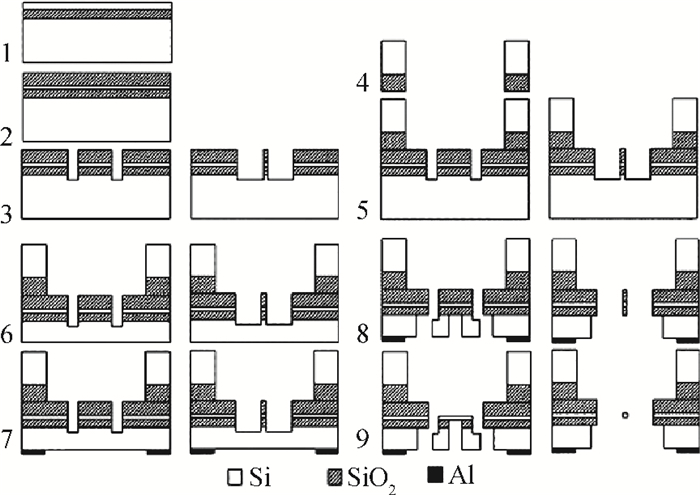
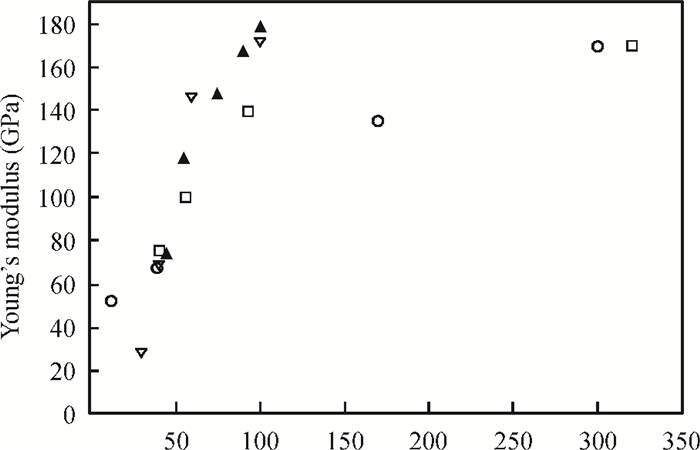
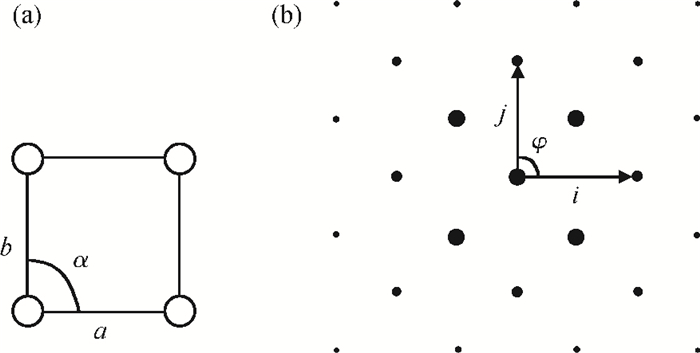
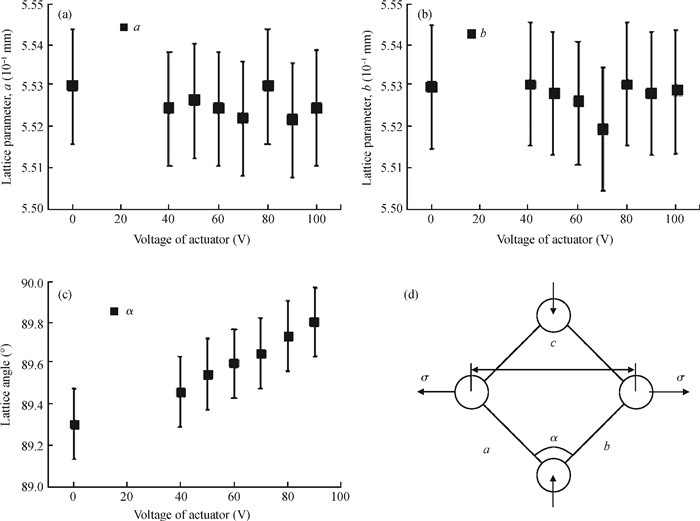
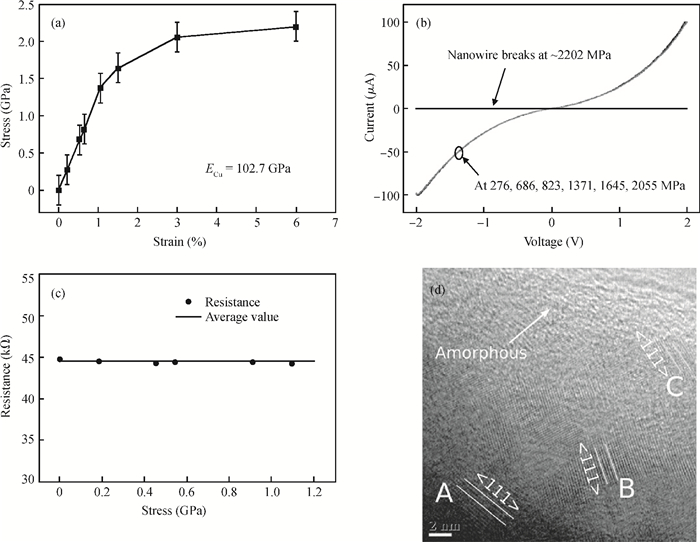
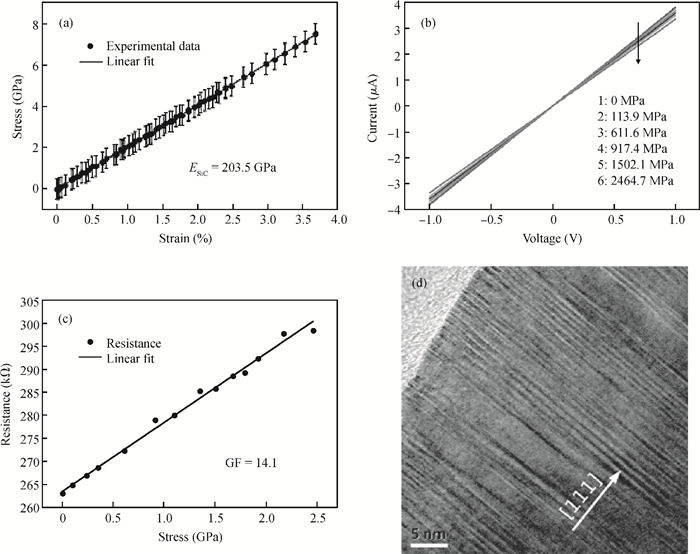
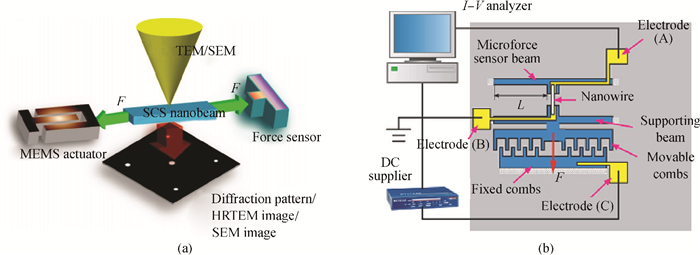
Our investigation of in situ observations on electronic and mechanical properties of nano materials using a scanning electron microscope (SEM) and a transmission electron microscope (TEM) with the help of traditional micro-electro-mechanical system (MEMS) technology has been reviewed. Thanks to the stability, continuity and controllability of the loading force from the electrostatic actuator and the sensitivity of the sensor beam, a MEMS tensile testing chip for accurate tensile testing in the nano scale is obtained. Based on the MEMS chips, the scale effect of Young's modulus in silicon has been studied and confirmed directly in a tensile experiment using a transmission electron microscope. Employing the nanomanipulation technology and FIB technology, Cu and SiC nanowires have been integrated into the tensile testing device and their mechanical, electronic properties under different stress have been achieved, simultaneously. All these will aid in better understanding the nano effects and contribute to the designation and application in nano devices. -
References
[1] Namazu T, Isono Y, Tanaka T. Evaluation of size effect on mechanical properties of single crystal silicon by nanoscale bending test using AFM. J Microelectromech Syst, 2000, 9:450 doi: 10.1109/84.896765[2] Jin Q H, Li T, Wang Y L, et al. Young's modulus size effect of SCS nanobeam by tensile testing in electron microscopy. IEEE SENSORS Conf, Christchurch, New Zealand, 2009:205 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5398190[3] Li D, Wu Y, Kim P, et al. Thermal conductivity of individual silicon nanowires. Appl Phys Lett, 2003, 83:2934 doi: 10.1063/1.1616981[4] He R, Yang P. Giant piezoresistance effect in silicon nanowires. Nature Nanotechnol, 2006, 1:42 doi: 10.1038/nnano.2006.53[5] Ma D D D, Lee C S, Au F C K, et al. Small-diameter silicon nanowire surfaces. Science, 2003, 299:1874 doi: 10.1126/science.1080313[6] Bell D J, Lu T J, Fleck N A, et al. MEMS actuators and sensors:observations on their performance and selection for purpose. J Micromech Microeng, 2005, 15:S153 doi: 10.1088/0960-1317/15/7/022[7] Kiuchi M, Matsui S, Isono Y. Mechanical characteristics of FIB deposited carbon nanowires using an electrostatic actuated nano tensile testing device. J Microelectromech Syst, 2007, 16:191 doi: 10.1109/JMEMS.2006.889663[8] Haque M, Saif M. In-situ tensile testing of nano-scale specimens in SEM and TEM Exp. Mech. 2002, 42:123 https://experts.illinois.edu/en/publications/in-situ-tensile-testing-of-nano-scale-specimens-in-sem-and-tem[9] Han J H, Saif M T. In situ microtensile stage for electromechanical characterization of nanoscale freestanding films. Rev Sci Instrum, 2006, 77:045102 doi: 10.1063/1.2188368[10] Zhu Y, Espinosa H D. An electromechanical material testing system for in situ electron microscopy and applications. P Natl Acad Sci USA, 2005, 102:14503 doi: 10.1073/pnas.0506544102[11] Zhu Y, Ke C, Espinosa H D. Experimental techniques for the mechanical characterization of one-dimensional nanostructures. Exp Mech, 2007, 47:7 doi: 10.1007/s11340-006-0406-6[12] Peng B, Locascio M, Zapol P, et al. Measurements of near-ultimate strength for multiwalled carbon nanotubes and irradiation-induced crosslinking improvements. Nature Nanotechnol, 2008, 3:626 doi: 10.1038/nnano.2008.211[13] Zhang D, Breguet J M, Clavel R, et al. In situ electron microscopy mechanical testing of silicon nanowires using electrostatically actuated tensile stages. J Microelectromech Syst, 2010, 19:663 doi: 10.1109/JMEMS.2010.2044746[14] Zhang D, Drissen W, Breguet J M, et al. A high-sensitivity and quasi-linear capacitive sensor for nanomechanical testing applications. J Micromech Microeng, 2009, 19:075003 doi: 10.1088/0960-1317/19/7/075003[15] Zeng H, Li T, Malte B, et al. In situ SEM electromechanical characterization of nanowire using an electrostatic tensile device. J Phys D:Appl Phys, 2013, 46:30551 http://adsabs.harvard.edu/abs/2013JPhD...46D5501Z[16] Jin Q, Wang Y, Li T, et al. A MEMS device for in-situ TEM test of SCS nanobeam. Sci China Ser E Technol Sci, 2008, 51:1491 doi: 10.1007/s11431-008-0123-8[17] Jin Q, Li T, Wang Y, et al. In-situ TEM tensile test of 90 nm thick < 110 > SCS beam using MEMS chip. Proc IEEE Sensors, Lecce, Italy, 2008:1116 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4716636[18] Guo Z, Wang X, Yang X, et al. Relationships between young's modulus, hardness and orientation of grain in polycrystalline copper. Acta Metall Sin, 2008, 44:901 http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-JSXB200808003.htm[19] Jin Q, Li T, Wang Y, et al. Confirmation on the size-dependence of Young's modulus of single crystal silicon from the TEM tensile tests. Proc IEEE Sensors, Hawaii, USA, 2010:2530 http://ieeexplore.ieee.org/document/5690465/[20] Jin Q, Li T, Zhou P, et al. Mechanical researches on Young's modulus of SCS nanostructures. J Nanomater, 2009, 2009:319842 http://dl.acm.org/citation.cfm?id=1705441[21] Li X, Ono T, Wang Y L, et al. Ultrathin single crystalline-silicon cantilever resonators:fabrication technology and significant specimen size effect on Young's modulus. Appl Phys Lett, 2003, 83:3081 doi: 10.1063/1.1618369[22] Sadeghian H, Yang C K, Goosen J F L, et al. Characterizing size-dependent effective elastic modulus of silicon nanocantilevers using electrostatic pull-in instability. Appl Phys Lett, 2009, 94:221903 doi: 10.1063/1.3148774[23] Bartenwerfer M, Fatikow S, Zeng H, et al. Individual nanowire handling for NEMS fabrication. IEEE/ASME Int Conf on Advanced Intelligent Mechatronics, Kaohsiung, Taiwan, 2012:562 http://ieeexplore.ieee.org/document/6266052/[24] Cao A, Wei Y, Ma E. Grain boundary effects on plastic deformation and fracture mechanisms in Cu nanowires:molecular dynamics simulations. Phys Rev B, 2008, 77:195429 doi: 10.1103/PhysRevB.77.195429[25] Cao H, Wang L, Qiu Y, et al. Synthesis and I-V properties of aligned copper nanowires. Nanotechnology, 2006, 17:1736 doi: 10.1088/0957-4484/17/6/032[26] John C, Kenneth J. Physics. 4th ed. New York:Wiley, 1998:755[27] Huang Q, Lilley C M, Bode M, et al. Electrical failure analysis of Au nanowires. 8th IEEE Conf on Nanotechnology, Arlington, TX, 2008:549[28] Perisanu S, Gouttenoire V, Vincent P, et al. Mechanical properties of SiC nanowires determined by scanning electron and field emission microscopies. Phys Rev B, 2008, 77:165434 doi: 10.1103/PhysRevB.77.165434[29] Petrovic J J, Milewski J V, Rohr D L, et al. Tensile mechanical-properties of SiC whiskers. J Mater Sci, 1985, 20:1167 doi: 10.1007/BF01026310[30] Wang J, Lu C, Wang Q, et al. Understanding large plastic deformation of SiC nanowires at room temperature. Europhys Lett, 2011, 95:63003 doi: 10.1209/0295-5075/95/63003[31] Wang S, Chung D D L. Piezoresistivity in silicon carbide fibers. J Electroceram, 2003, 10:147 doi: 10.1023/B:JECR.0000011213.58831.45[32] Mukherjee M. Silicon carbide-materials, processing and applications in electronic devices. Rijeka:In Tech, 2011:369[33] Shor J S, Bemis L, Kurtz A D. Characterization of monolithic n-type 6H-SiC piezoresistive sensing elements. IEEE Trans Electron Devices, 1994, 41:661 doi: 10.1109/16.285013 -
Proportional views





 DownLoad:
DownLoad: