| Citation: |
Xiaoguang Guo, Ziyuan Liu, Hang Gao, Dongming Guo. Nano-indentation study on the (001) face of KDP crystal based on SPH method[J]. Journal of Semiconductors, 2015, 36(8): 083007. doi: 10.1088/1674-4926/36/8/083007
****
X G Guo, Z Y Liu, H Gao, D M Guo. Nano-indentation study on the (001) face of KDP crystal based on SPH method[J]. J. Semicond., 2015, 36(8): 083007. doi: 10.1088/1674-4926/36/8/083007.
|
Nano-indentation study on the (001) face of KDP crystal based on SPH method
DOI: 10.1088/1674-4926/36/8/083007
More Information
-
Abstract
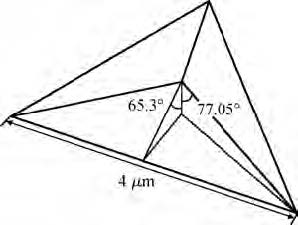
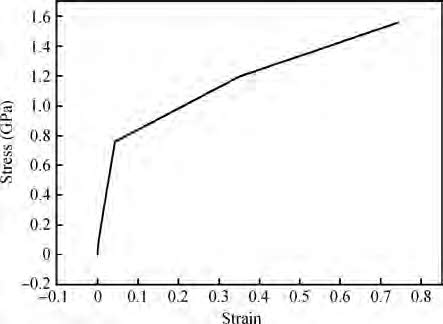
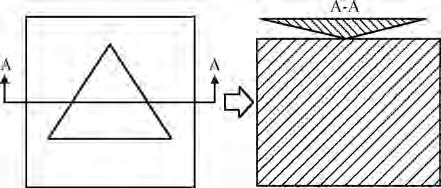
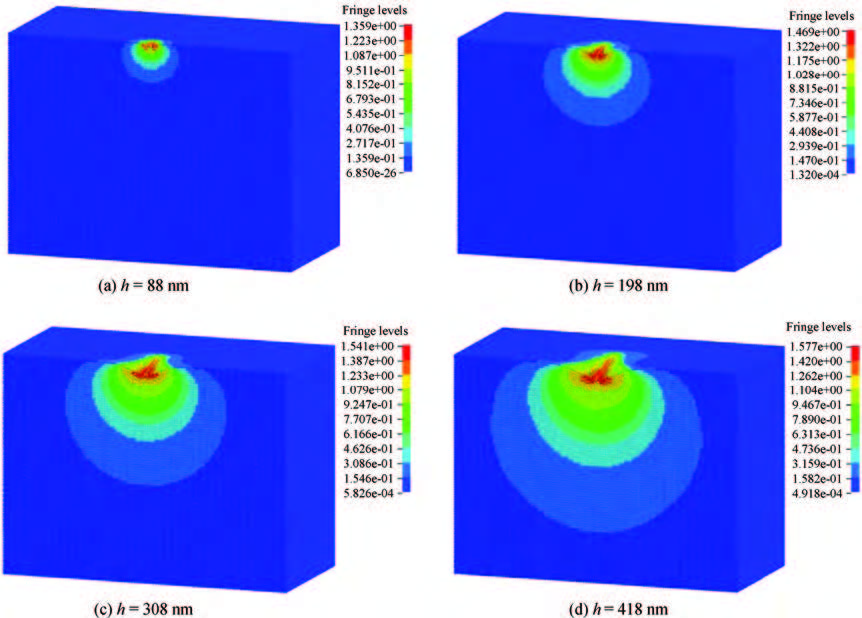
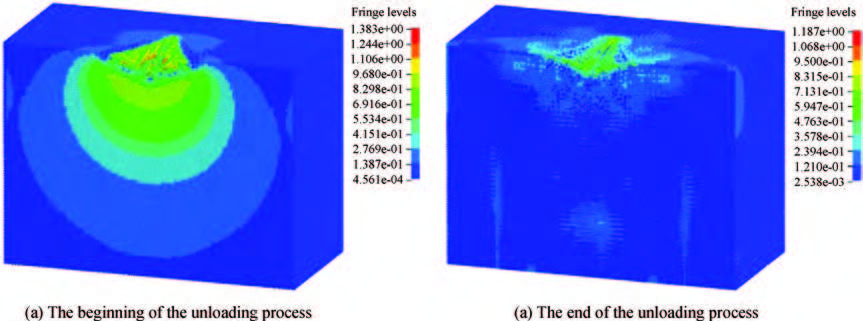
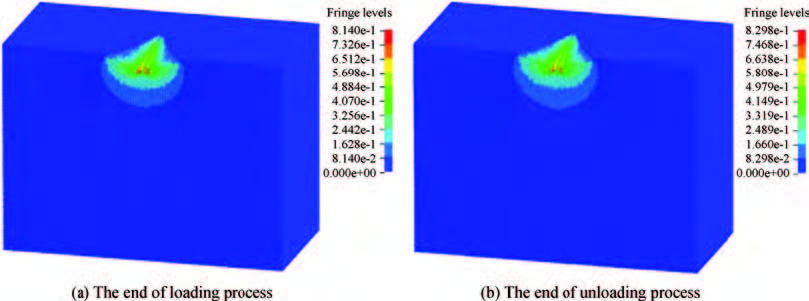
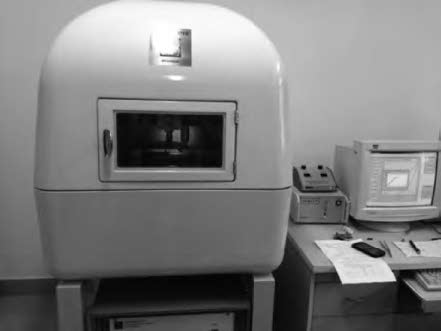
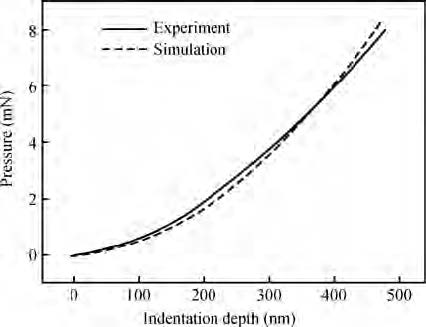
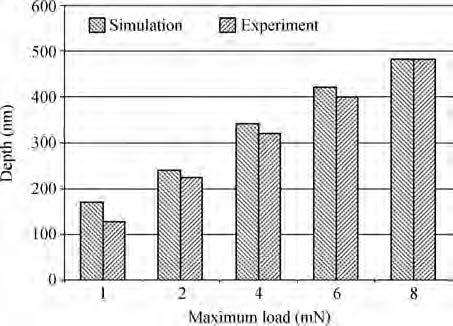
In order to avoid the defects of mesh distortion when dealing with large deformation problems through using the finite element method, a mess-free simulation method——smooth particle hydrodynamics (SPH) has been introduced. The material constitutive model of KDP crystal has been established based on the elastic-plastic theory. Then the nano-indentation on the (001) face of KDP crystal has been carried out using SPH method. Simulation results show that the maximum equivalent stress and the maximum plastic strain concentrate on the area that located near the tip of the indenter during the loading process. The distribution shape of Von Mises stress is similar to concentric circles. During the unloading process, no obvious variation of plastic strain distribution exists. The maximum Von Mises stress is mainly located at the indentation and its edge at the end of the unloading process. The approximate direct proportion relationship between the maximum indentation depth and the depth of the maximum Von Mises stress distribution has been discovered when the maximum load is lower than 8 mN. In addition, the nano-indentation experiments on KDP crystal's (001) face have been carried out. Both the material parameters and the adjusted stress-strain curve have been verified. The hindering role of the affected layer has been found and analyzed.-
Keywords:
- KDP crystal,
- (001) face,
- nano-indentation,
- SPH,
- numerical simulation
-
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] -
Proportional views





 DownLoad:
DownLoad: