J. Semicond. > 2016, Volume 37 > Issue 1 > 014003
|

SEMICONDUCTOR DEVICES

Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys

Tangudu Bharat Kumar1, Bahniman Ghosh2, 3, Bhaskar Awadhiya4 and Ankit Kumar Verma5

+ Author Affiliations

 Corresponding author: Bahniman Ghosh,Email:

DOI: 10.1088/1674-4926/37/1/014003

PDF

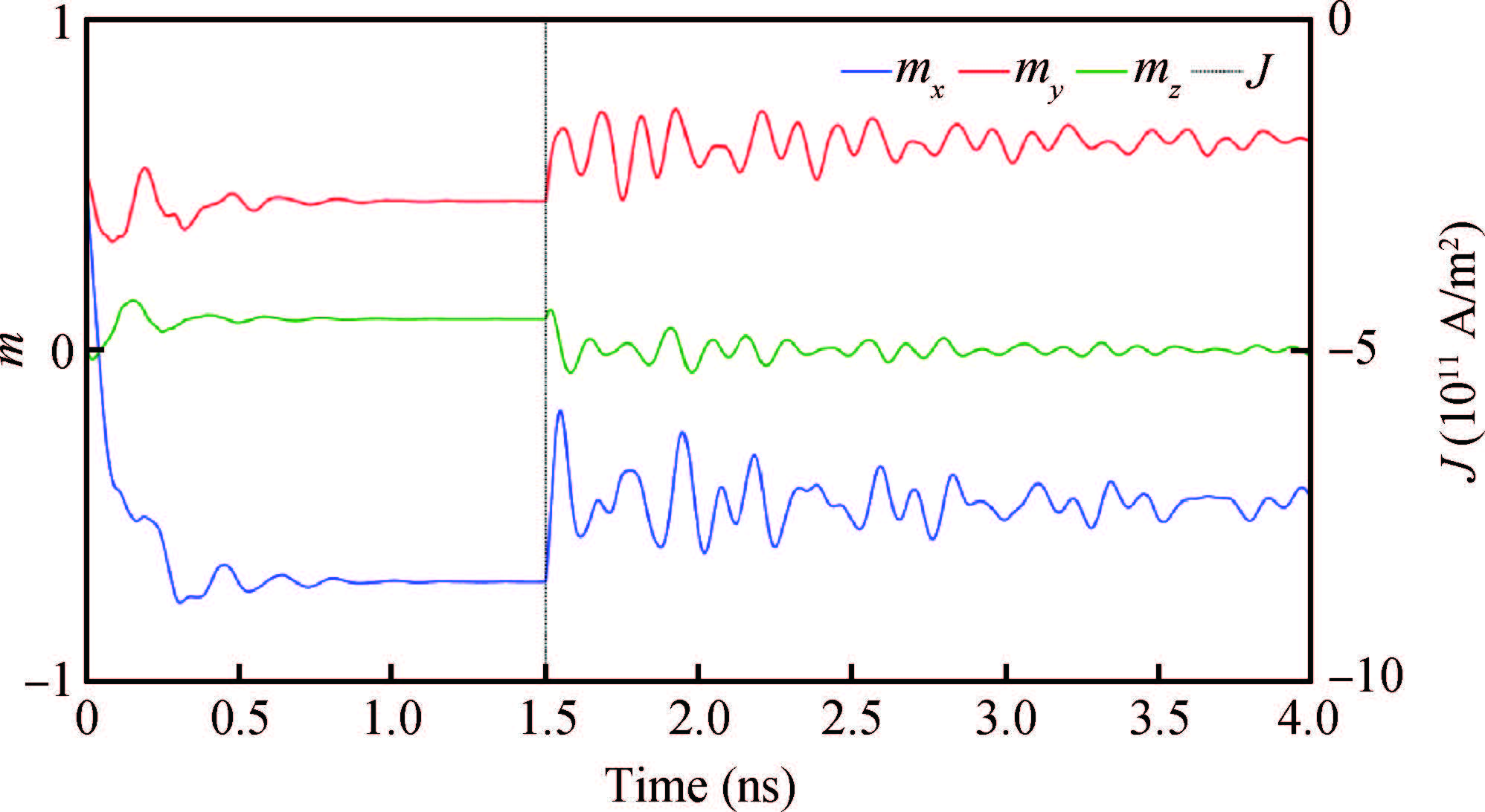
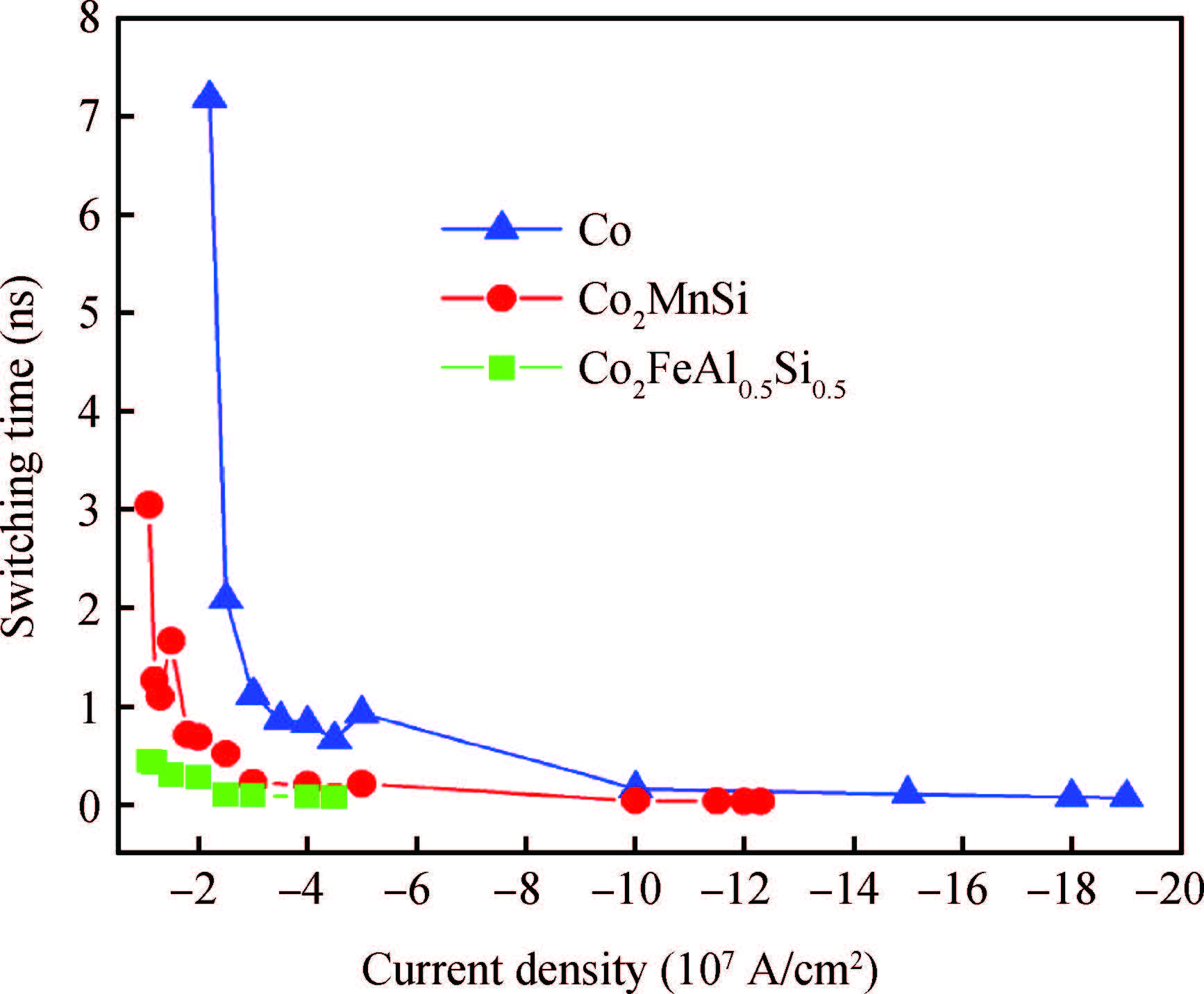
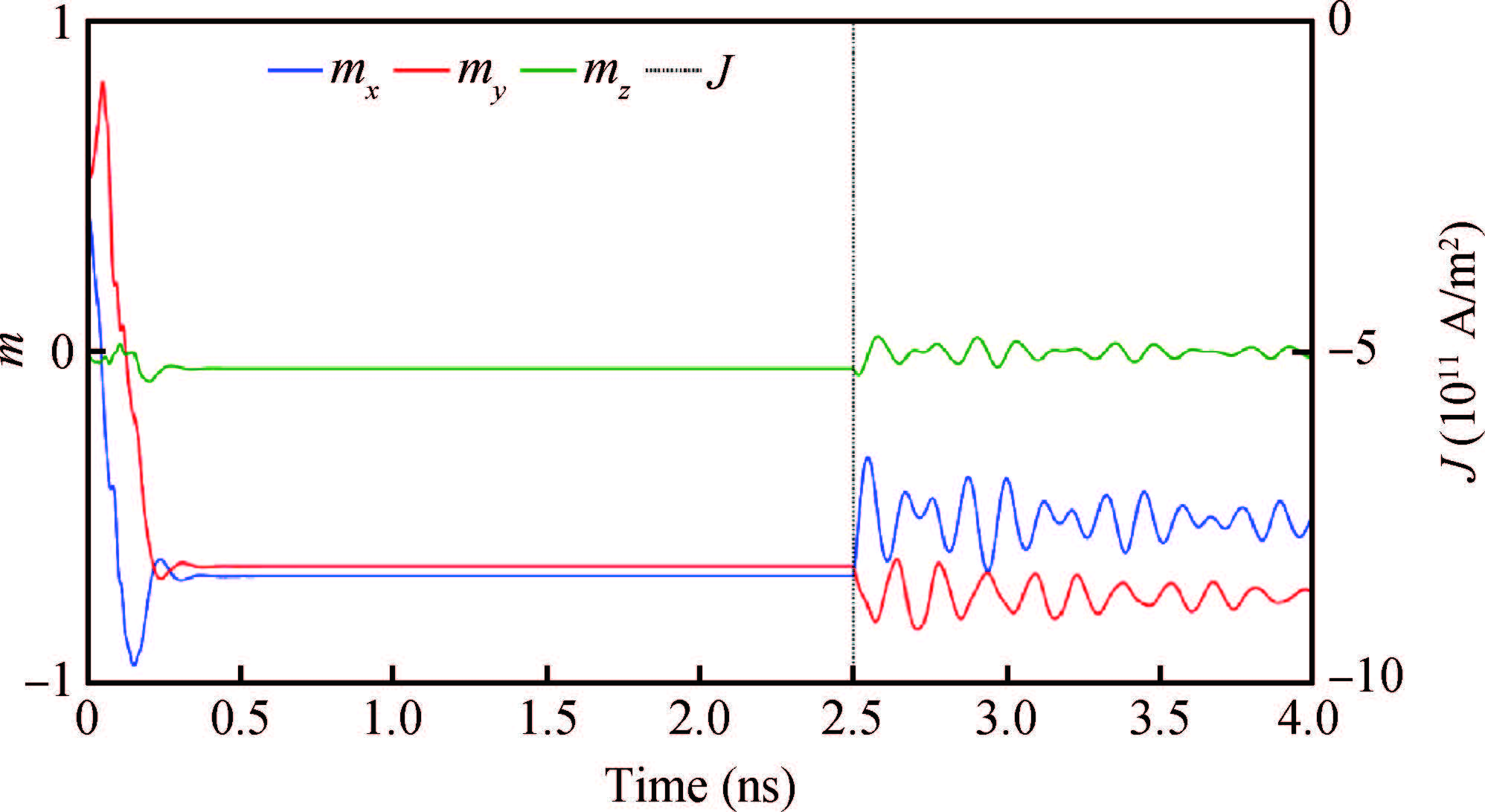
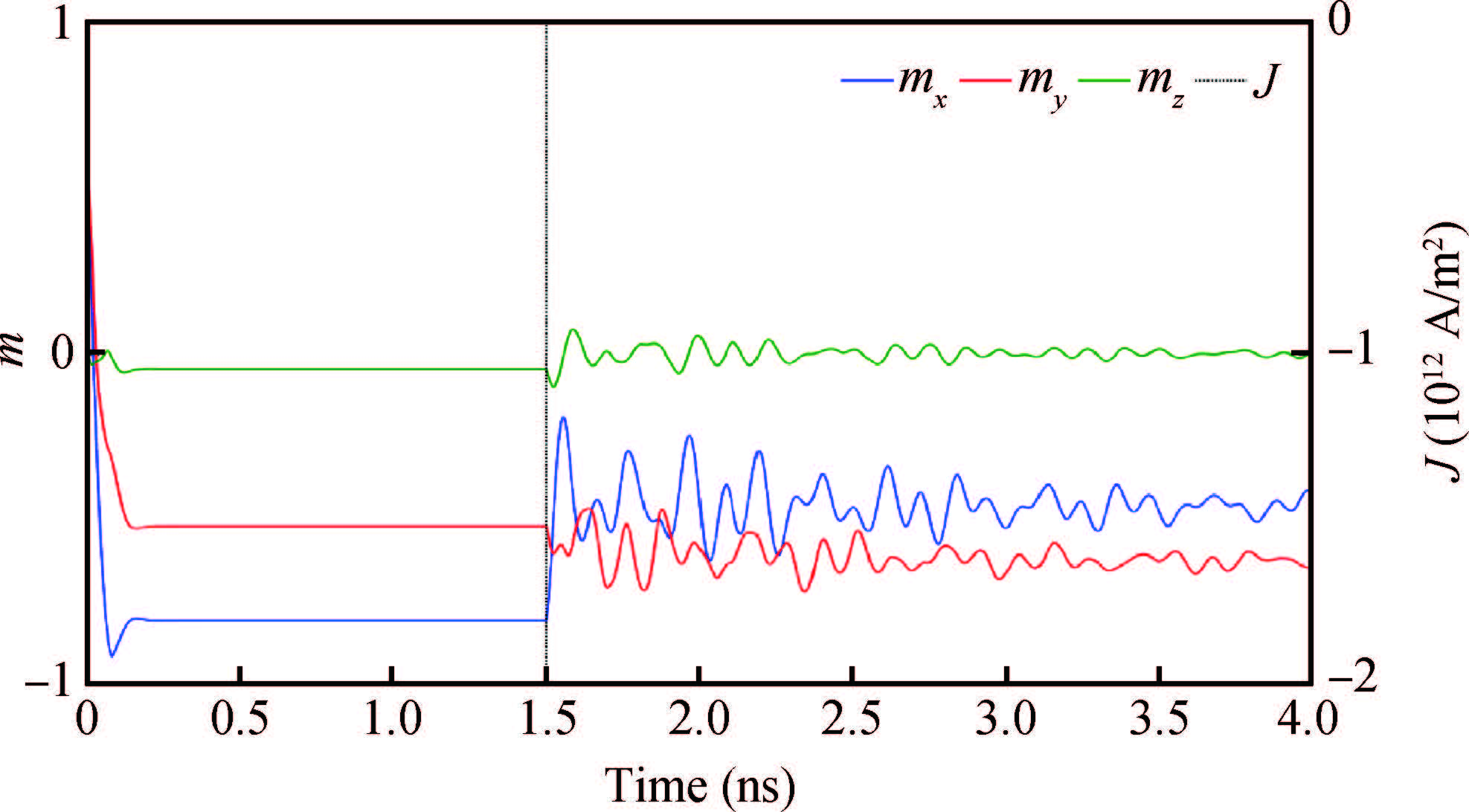
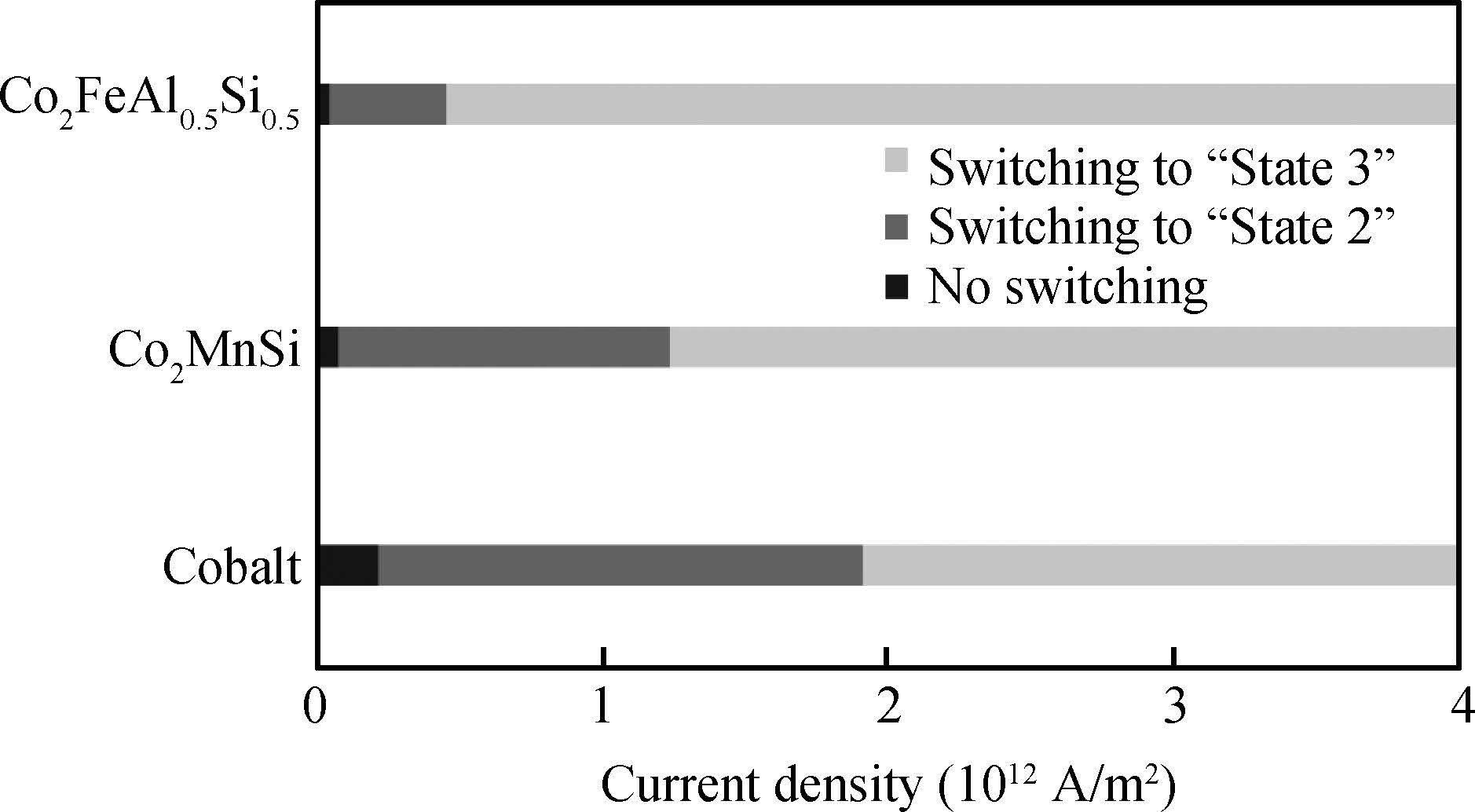
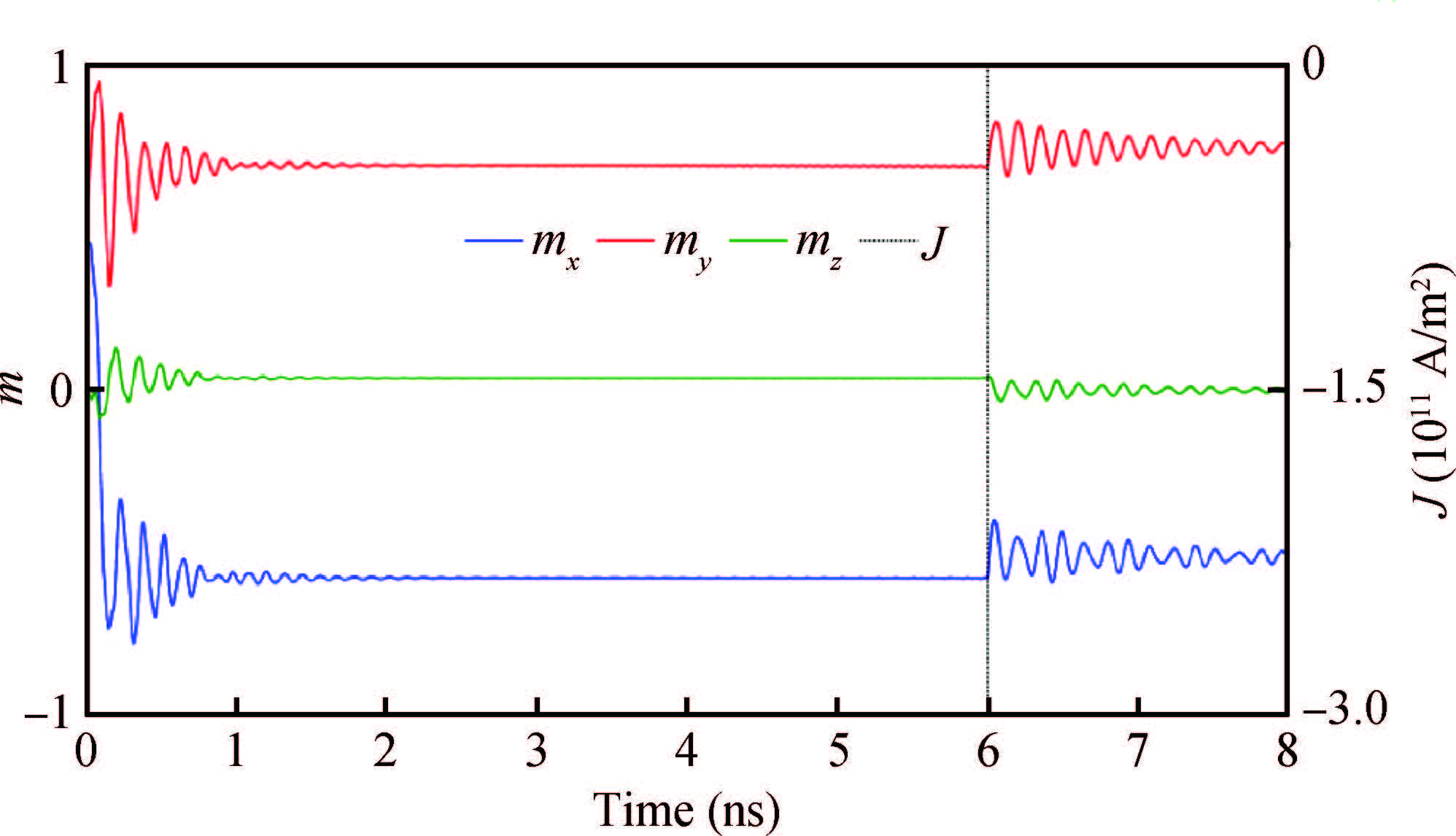
Abstract: We have investigated the performance of a spin transfer torque random access memory (STT-RAM) cell with a cross shaped Heusler compound based free layer using micromagnetic simulations. We have designed a free layer using a Cobalt based Heusler compound. Simulation results clearly show that the switching time from one state to the other state has been reduced, also it has been found that the critical switching current density (to switch the magnetization of the free layer of the STT RAM cell) is reduced.

Key words: spin transfer torque random access memory (STT-MRAM), micromagnetic simulation, Heusler compound, switching time, critical switching current density



[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
Fig. 1.  (Color online) CFAS based free layer switching from ‘state 1’ to ‘state 2’ at J = -3 × 1011 A/m2.

DownLoad: Full-Size Img PowerPoint
Fig. 2.  (Color online) CMS based free layer switching from ‘state 1’ to ‘state 2’ at J = -1 × 1012 A/m2.

DownLoad: Full-Size Img PowerPoint
Fig. 3.  (Color online) Variation of switching time from ‘state 1’ to ‘state 2’ with different current densities.

DownLoad: Full-Size Img PowerPoint
Fig. 4.  (Color online) CFAS based free layer switching from state 1 to state 3 at J = -1 × 1012 A/m2.

DownLoad: Full-Size Img PowerPoint
Fig. 5.  (Color online) CMS based free layer switching from ‘state 1’ to ‘state 3’ at J = -2 × 1012 A/m2.

DownLoad: Full-Size Img PowerPoint
Fig. 6.  Switching regions to ‘state 2’ and ‘state 3’ from ‘state 1’ by raising the current density values.

DownLoad: Full-Size Img PowerPoint
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]

    • Search

    Advanced Search >>

    GET CITATION

    shu

    Export: BibTex EndNote

    Article Metrics

    Article views: 2775 Times PDF downloads: 24 Times Cited by: 0 Times

    History

    Received: 28 February 2015 Revised: Online: Published: 01 January 2016

    Catalog

      Email This Article

      User name:
      Email:*请输入正确邮箱
      Code:*验证码错误
      Send
      Article Navigation >  Journal of Semiconductors  > 2016  >  37(1): 014003
      Tangudu Bharat Kumar, Bahniman Ghosh, Bhaskar Awadhiya, Ankit Kumar Verma. Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys[J]. Journal of Semiconductors, 2016, 37(1): 014003. doi: 10.1088/1674-4926/37/1/014003 ****T B Kumar, B Ghosh, B Awadhiya, A K Verma. Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys[J]. J. Semicond., 2016, 37(1): 014003. doi: 10.1088/1674-4926/37/1/014003.
      Citation:
      Tangudu Bharat Kumar, Bahniman Ghosh, Bhaskar Awadhiya, Ankit Kumar Verma. Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys[J]. Journal of Semiconductors, 2016, 37(1): 014003. doi: 10.1088/1674-4926/37/1/014003 ****
      T B Kumar, B Ghosh, B Awadhiya, A K Verma. Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys[J]. J. Semicond., 2016, 37(1): 014003. doi: 10.1088/1674-4926/37/1/014003.
      shu

      Performance analysis of STT-RAM with cross shaped free layer using Heusler alloys

      DOI: 10.1088/1674-4926/37/1/014003
      • 1.

        Department of Electronics and Communications, Malaviya National Institute of Technology, Jaipur, India

      • 2.

        Microelectronics Research Center, 10100 Burnet Road, Bldg. 160, University of Texas at Austin, Austin, TX, 78758, USA

      • 3.

        Department of Electrical Engineering, Indian Institute of Technology Kanpur, Kanpur 208016, India

      • 4.

        Department of Electronics and Communications, Manipal Institute of Technology, Manipal University, Manipal, India

      • 5.

        Electronics and Communication Engineering Department, National Institute of Technology, Hamirpur, Himachal Pradesh, India

      More Information

      Catalog

        Journal of Semiconductors © 2017 All Rights Reserved   京ICP备05085259号-2

        /

        DownLoad:  Full-Size Img  PowerPoint
        Return
        Return