1. Introduction

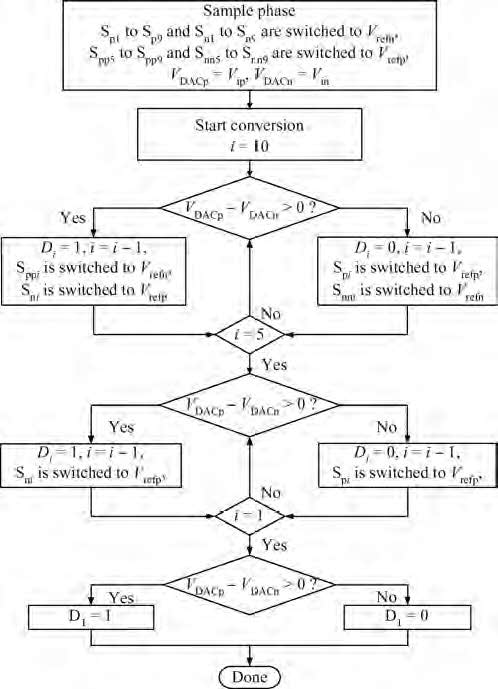
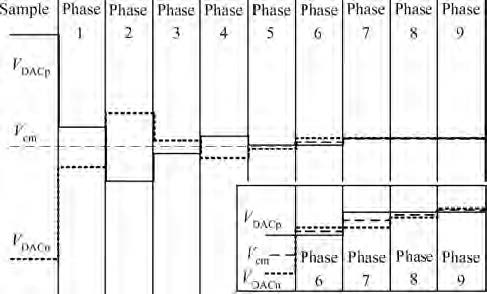
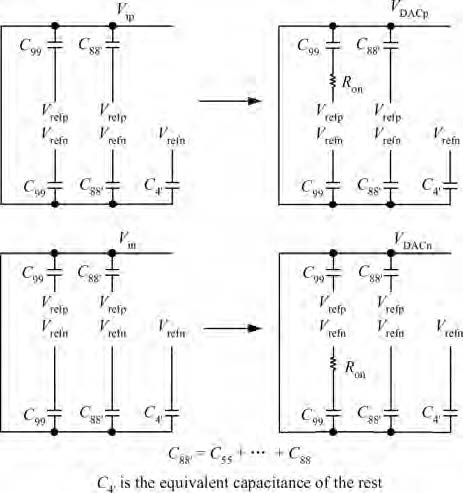
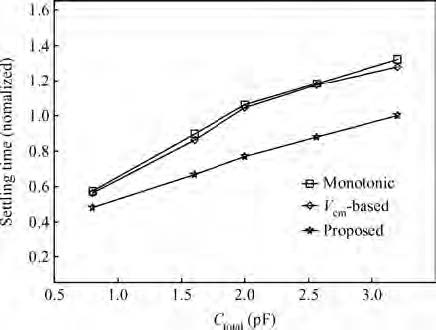
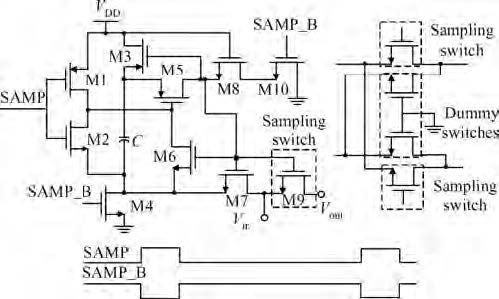
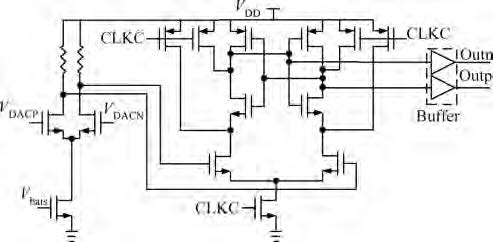
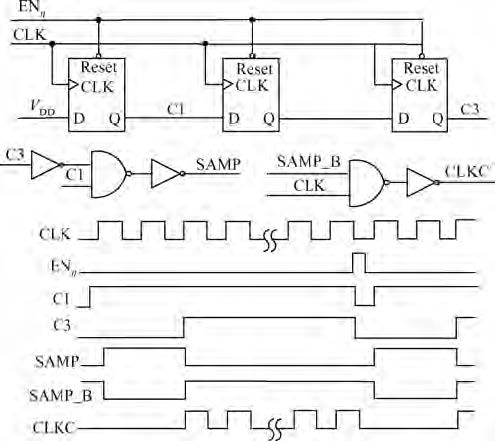
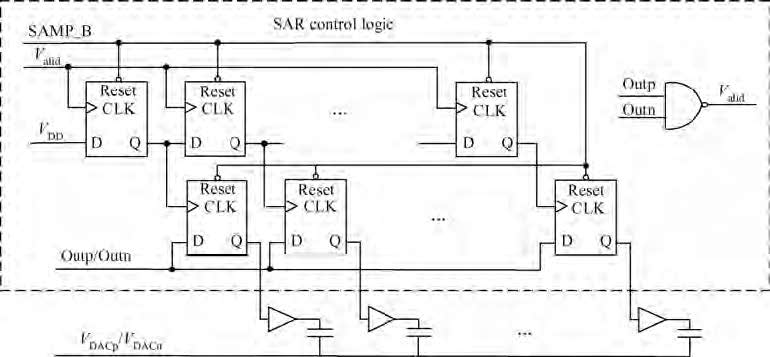
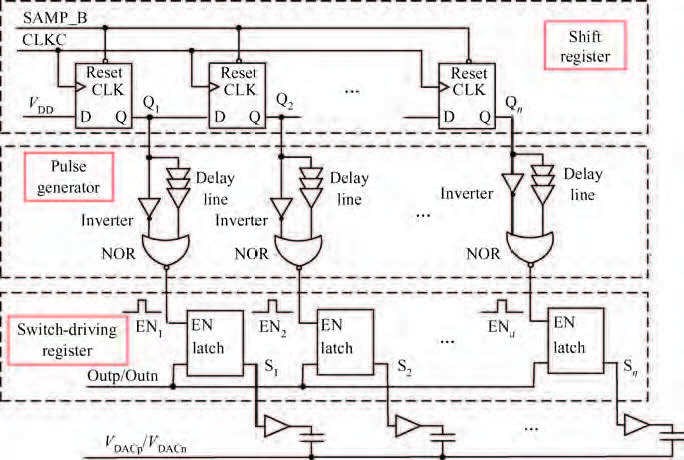
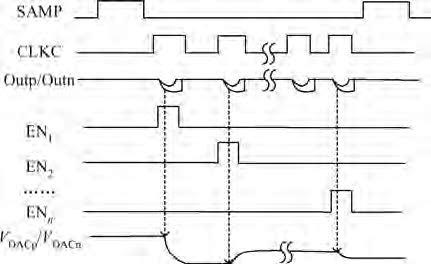
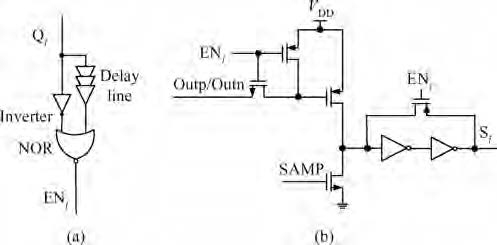
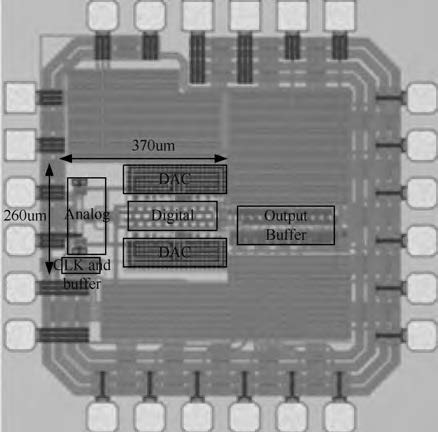
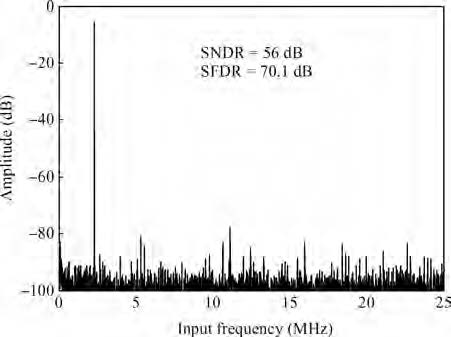
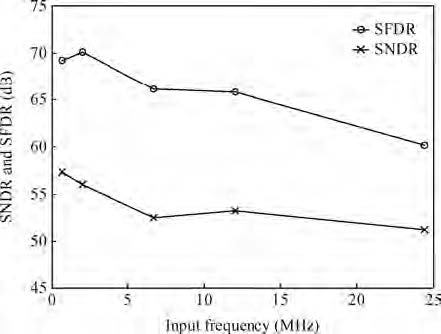
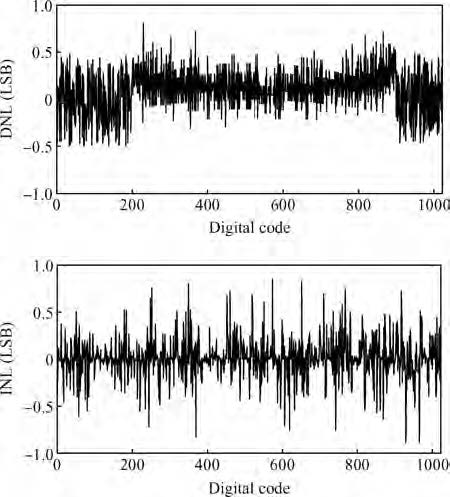
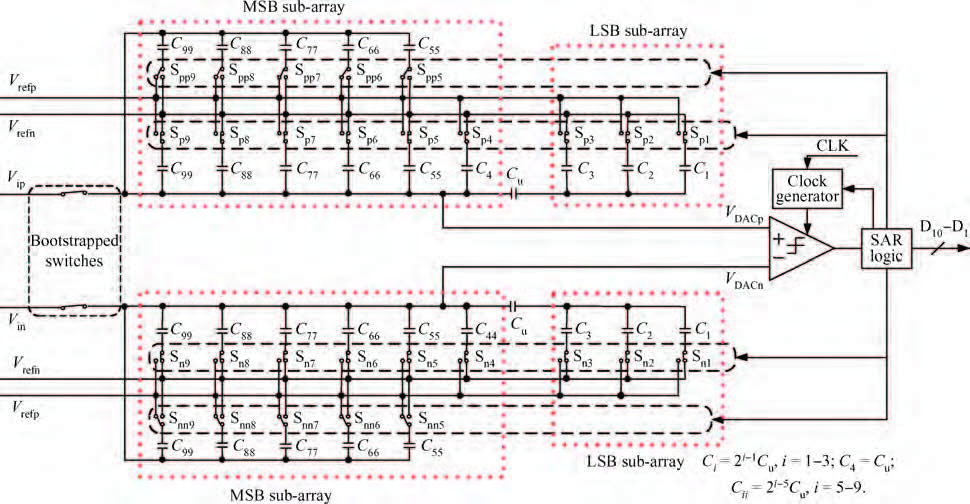
Consisting of a bootstrapped switch,comparator,capacitive digital-to-analog converter (DAC) and successive approximation register (SAR) control logic,SAR analog-to-digital converters (ADCs) have the advantages of minimal analog complexity and low power consumption^{[1, 2, 3, 4]}. On the other hand,SAR ADCs have limited operation speed due to their serial operation principle. Thus,SAR ADCs are often used in low power and low speed applications. In recent years,with the scaling of the feather size of CMOS process,the conversion speed of SAR ADCs have been improved to several tens to hundreds of MS/s with 5 to 10 bit resolution in sub-micrometer technology^{[5, 6, 7, 8]}. Therefore,it is possible that the SAR ADC will be able to replace the pipelined ADC in medium-resolution and mediate-speed applications.

In charge redistribution SAR ADCs,the total capacitance of the capacitor array grows exponentially as the resolution increases. It is well known that the switching energy of the capacitor array is proportional to the total capacitance. In high resolution SAR ADCs,the total capacitance becomes too large,thereby increasing the power consumption. On the other hand,the settling time of the DAC is determined by the time constant of charging or discharging capacitors,which is one of the dominant speed limiting factors of SAR ADCs. Thus,the large capacitance also limits the conversion speed. For a high resolution SAR ADC,the segmented architecture DAC with a bridged capacitor has been used to significantly reduce the total capacitance leading to a reduction in power consumption and improved conversion speed^{[1, 2, 3, 4]}.

In this paper,a segmented architecture DAC with a partial split capacitor switching scheme is proposed to further improve the conversion speed of SAR ADC. This method reduces the equivalent input capacitance in the first few most significant bits (MSBs) conversions,and so the settling time of DAC is reduced,thereby improving the conversion speed. In addition,the delay time of logic control circuits is also one of the dominant speed limiting factors of a SAR ADC^[9]. This paper presents a new SAR control logic to boost conversion speed by minimizing the delay time from the comparator to DAC. The 10 bit SAR ADC is fabricated in 0.18 $\mu$m CMOS process with a 1.8 V supply voltage. At 50 MS/s,the SAR ADC achieves 57.5 dB SNDR with 2.26 mW power consumption.

2. ADC architecture

The architecture of the proposed 10 bit SAR ADC is shown in Figure1. Unlike the conventional segmented capacitive DAC,the capacitors of the first few MSBs in the proposed DAC are all split into two equal parts. During the sample phase,the differential input signals are sampled on the top plates of the MSB sub-array via bootstrapped switches. S$_{\rm p1}$ to S$_{\rm p9}$ and S$_{\rm n1}$ to S$_{\rm n9}$ are switched to $V_{\rm refn}$. S$_{\rm pp5}$ to S$_{\rm pp9}$ and S$_{\rm nn5}$ to S$_{\rm nn9}$ are switched to $V_{\rm refp}$. Next,the bootstrapped switches are turned off and the SAR ADC starts the conversion phase. During the conversion phase,the capacitive DAC gradually reaches the sampled input voltage after ten comparisons for a 10-bit SAR ADC. In this design,the settling time of capacitive DAC is shortened by the proposed partial split capacitor switching scheme,which will be discussed in detail later.

3. Circuit design and consideration

3.1 DAC with partial split capacitor switching scheme

The flow chart of the proposed switching scheme is shown in Figure2. During the sample phase,the differential input signals are sampled on the top plates via bootstrapped switches. Meanwhile,S$_{\rm p1}$ to S$_{\rm p9}$ and S$_{\rm n1}$ to S$_{\rm n9}$ are switched to $V_{\rm refn}$,S$_{\rm pp5}$ to S$_{\rm pp9}$ and S$_{\rm nn5}$ to S$_{\rm nn9}$ are switched to $V_{\rm refp}$. Benefited from the top-plate sampling,the first comparison is carried out directly without any energy consumption. Thus,only 9 bit DAC is required for the 10 bit fully differential SAR ADC. If $V_{\rm DACp}$ is larger than $V_{\rm DACn}$,S$_{\rm pp9}$ will be switched to $V_{\rm refn}$ and S$_{\rm n9}$ will be switched to $V_{\rm refp}$. Otherwise,S$_{\rm nn9}$ will be switched to $V_{\rm refn}$ and S$_{\rm p9}$ will be switched to $V_{\rm refp}$. The ADC repeats this procedure until the 5th comparison is done. Next,if $V_{\rm DACp}$ is larger than $V_{\rm DACn}$ in the step of 6th comparison,S$_{\rm n4}$ will be switched to $V_{\rm refp}$. Otherwise,S$_{\rm p4}$ is switched to $V_{\rm refp}$. This procedure will be repeated until the 9th comparison is completed. Then,the least significant bit (LSB) is achieved by the 10th comparison and is directly output without any change in the capacitive DAC.

The value of the input voltage ranges from --$V_{\rm ref}$ to $V_{\rm ref}$,where $V_{\rm ref}=V_{\rm refp}-V_{\rm refn}$. At the end of the bit cycling,the remaining voltage is given by

$$\begin{align} V_{\rm e}=(V_{\rm ip}-V_{\rm in})+(1-D_{10})V_{\rm ref}- \sum^9_{i=1}D_iW_i, \end{align}$$

(1)

where $D_{10}$ is the MSB,which is either 0 or 1,$D_{i}$ is the rest output code from the SAR ADC for bit $i$,either 0 or 1,and $W_{i}$ is the capacitor weights. $D_{10}$ $=$ 1 represents the positive input voltage and $D_{10}$ $=$ 0 represents the negative input voltage. The weights for the MSB sub-array and LSB sub-array are given by

$$\begin{align} W_{i,{\rm M}}= \begin{cases} \dfrac{2C_{ii}(C_{\rm u}+C_{\rm LSB})}{C_{\rm MSB}C_{\rm LSB}+C_{\rm u}(C_{\rm MSB}+C_{\rm LSB})}V_{\rm ref},\\[2mm] \qquad\qquad \qquad i=5,\cdots,9, \\[4mm] \dfrac{C_{i}(C_{\rm u}+C_{\rm LSB})}{C_{\rm MSB}C_{\rm LSB}+C_{\rm u}(C_{\rm MSB}+C_{\rm LSB})}V_{\rm ref},\quad i=4, \end{cases} \end{align}$$

(2)

$$\begin{align} W_{i,{\rm L}}=\frac{C_iC_{\rm u}}{C_{\rm MSB}C_{\rm LSB}+C_{\rm u}(C_{\rm MSB}+C_{\rm LSB})}V_{\rm ref},\quad i=1,2,3, \end{align}$$

(3)

where $C_{\rm MSB}$ and $C_{\rm LSB}$ are the total capacitance in the MSB sub-array and LSB sub-array,respectively.

Figure3 shows the output waveform of the DAC with the proposed switching scheme. As can be seen,the output common-mode voltage almost keeps stable,unlike the monotonic switching method^[6]. It remains unchanged until the last four conversion procedures and the maximum variation is only 4 LSB. Thus,the input common-mode voltage of the comparator is almost a constant,making the comparator's realization more relaxed^[8].

For the trade-offs among speed,area,and power,the settling time of the DAC is often chosen to be fixed for all bit cycles^[10]. Thus,the total settling time is determined by the longest bit cycle. For a fully differential SAR ADC using top-plate sampling,the longest bit cycle occurs when $V_{\rm step}$ $=$ $\frac{1}{4}V_{\rm FS}$. $V_{\rm step}$ is the DAC settling step voltage and $V_{\rm FS}$ $=$ 2($V_{\rm refp}-V_{\rm refn})$,which is the full scale voltage. Assuming that $V_{\rm ip}$ is larger than $V_{\rm in}$,S$_{\rm pp9}$ is switched to $V_{\rm refn}$ and S$_{\rm n9}$ is switched to $V_{\rm refp}$. The equivalent circuit during the longest settling procedure of the proposed DAC is shown in Figure4.

By using Laplace transform,the output voltage of the DAC is evaluated

$$\begin{align} V_{\rm DAC1}=V_{\rm DACp}-V_{\rm DACn}=(V_{\rm ip}-V_{\rm in})-\frac{1}{4}\left(1-{\rm e}^{-\frac{t}{\tau_1}} \right)V_{\rm FS}, \end{align}$$

(4)

where $\tau_{1}$ denotes the time constant of the longest bit cycle and is derived by

$$\begin{align} \tau_1=\frac{3}{4}R_{\rm on}C_{99}\approx \frac{3}{16}R_{\rm on}C_{\rm tot}, \end{align}$$

(5)

where $R_{\rm on}$ is the equivalent turn-on resistance of the switch in the DAC and $C_{\rm tot}$ is the total equivalent capacitance of the DAC capacitor array. Thus,the settling time of the longest bit cycle is

$$\begin{align} t_{\rm DAC1}=\tau_1\ln \frac{V_{\rm step}}{\varepsilon}=\tau_1 \ln \frac{\dfrac{1}{4}V_{\rm FS}}{\varepsilon}, \end{align}$$

(6)

where $\varepsilon$ is the settling error which should be less than $\frac{1}{2}$LSB.

In order to discuss the advantage of the fast settlement of the proposed switching scheme,the settling times of the monotonic switching scheme^[6] and the $V_{\rm cm}$-based switching method^[7] are also analyzed. Some assumptions are pre-set before the analysis. First,let the total capacitance ($C_{\rm tot})$ of the DAC applied for all of the switching techniques be the same. Second,the switches connecting the capacitors are sized to give the same resistance as $R_{\rm on}$ for these switching schemes. By using the same method,the settling times of the longest bit cycle in the other two switching schemes are both derived as

$$\begin{align} t_{\rm DAC2}=\tau_2\ln \frac{V_{\rm step}}{\varepsilon}=\tau_2 \ln \frac{\dfrac{1}{4}V_{\rm FS}}{\varepsilon}, \end{align}$$

(7)

with

$$\begin{align} \tau_2 \approx \frac{1}{4}R_{\rm on}C_{\rm tot}. \end{align}$$

(8)

It is shown that the time constant of the longest bit cycle in the proposed technique is reduced by 25{\%} compared with the monotonic switching scheme and the $V_{\rm cm}$-based switching method,resulting in a 25{\%} reduction in settling time of DAC. DACs that use the proposed switching scheme,monotonic switching technique,and the $V_{\rm cm}$-based switching technique are implemented in TSMC 180 nm CMOS process as examples to validate this idea. A comparison of the settling time of these techniques against the total capacitance is shown in Figure5. It is shown that the proposed switching technique has the shortest settling time.

On the other hand,the minimum value of the unit capacitor is determined by the capacitor mismatch^{[11, 12]}. According to Reference ^[13],the unit capacitor in the bridged capacitor array should be larger than the one in the binary capacitor array due to the more stringent matching requirement. But the values of the capacitors in the MSB sub-array are scaled down for the bridged capacitor array. So,a reasonable larger unit capacitor can be chosen to satisfy the matching requirement and achieve a smaller total capacitance compared with the binary capacitor array. In this design,the metal--insulator--metal (MIM) capacitors are used to construct the capacitor array. In order to meet the matching requirement for the 10 bit resolution,the unit capacitance is designed to be 50 fF.

3.2 Bootstrapped switch

Figure6 shows the schematic of the bootstrapped switch. When the sample signal (SAMP) goes high,M5 and M7 turn-on. The gate and source of the sampling switch are connected via the bootstrapped capacitor,resulting in a fixed voltage between the gate and source. So,the on-resistance of the sampling switch is fixed at a constant value,which improves the linearity of the sampling switch. As reported in Reference ^[6],two cross-coupled metal--oxide--metal (MOM) capacitors are used to reduce the signal feed-through effect. In this paper,two dummy switches are used to replace the MOM capacitors to reduce this effect.

3.3 Comparator

A dynamic comparator with a pre-amplifier is used in the proposed SAR ADC and the schematic of the comparator is illustrated in Figure7. The pre-amplifier is used to block the kickback noise and enhance the comparison speed. In this design,a synchronous clock generator is used to generate the comparator clock (CLKC),as shown in Figure8. The CLK is the high speed input clock signal. The EN$_{n}$ is generated in the SAR control logic circuit during the last bit conversion,which will be explained in detail later. It will be used for a reset signal to start the next sample.

3.4 SAR control logic

The conventional SAR control logic circuit consists of a shift register and a switch-driving register (SDR)^[6],as shown in Figure9. The shift register is used to generate the multi-phase clocks,which is triggered by completion signal (Valid) of the comparison. These multi-phase clocks are used to trigger the SDR,which is used to control the charging or discharging of the capacitor array. The conventional SAR control logic delay ($t_{\rm logic})$ consists of the delay of the comparator output buffer,the delay of the NAND gate ($t_{\rm NAND})$ (which generates the Valid signal),the delay of the shift register ($t_{\rm DFF,shift})$,and the delay of the SDR ($t_{\rm DFF,SDR})$. So the logic delay can be achieved:

$$\begin{align} t_{\rm logic}=t_{\rm buf}+t_{\rm NAND}+t_{\rm DFF,shift}+t_{\rm DFF,SDR}. \end{align}$$

(9)

In order to achieve high speed conversion,the logic delay should be reduced. A novel logic control scheme is proposed,as shown in Figure10. The proposed logic control circuit consists of a shift register,a pulse signal generator,and a SDR that consist of a row of latches. After the sample phase,the bit cycling begins immediately. When CLKC goes high and triggers the first D flip--flop (DFF),a high level voltage will be generated which passes through the first pulse generator to generate a pulse signal (EN$_{1})$. Then,the EN$_{1}$ signal enables the first latch to wait for the comparison result. The first latch will be locked and stores the MSB comparison result until the next sample phase. When CLKC goes high again,this control procedure repeats to generate the next bit control signal. In this way,$n$-bit cycling completes in a serial manner. Figure11 shows the timing diagram of the principle of the proposed SAR control logic. It is shown that the generated procedure of the pulse signal and the regeneration of the comparator are simultaneous. In other words,only the SDR is in the critical path. Therefore,the logic delay of the proposed logic control scheme ($t_{\rm logic,pro})$ can be achieved

$$\begin{align} t_{\rm logic,pro}=t_{\rm buf}+t_{\rm latch,SDR}, \end{align}$$

(10)

where $t_{\rm latch,SDR}$ is the delay time of the latch in SDR and $t_{\rm buf}$ is the delay of the comparator output buffer as the conventional logic. The schematics of the pulse generator and the latch are depicted in Figure12. By comparing Equations (9) and (10),it can be seen that the logic delay of the proposed method is reduced significantly.

4. Experimental results

The proposed 10 bit SAR ADC is fabricated in TSMC 1P6M 0.18 $\mu$m CMOS process with a 1.8 V supply. The chip microphotograph is shown in Figure13. The total die size is 1.05 $\times$ 1.05 mm$^{2}$ and the ADC core occupies only 0.096 mm$^{2}$. The measured SFDR is 70.1 dB and SNDR is 56 dB when a 2.02 MHz input signal is sampled at 50 MS/s,as shown in Figure14. Figure15 shows the measured SFDR and SNDR versus the input signal frequency swept from 0.677 MHz to Nyquist. At 0.677 MHz input signal frequency,the measured SFDR and SNDR are 69.3 and 57.5 dB,respectively. When the input signal frequency is up to 25 MHz,the SFDR and SNDR are decreased to be 60.2 and 51.2 dB,respectively.

According to Figure16,the DNL is $-0.49$/$+0.76$ LSB and the INL is $-0.89$/$+0.85$ LSB. Table1 summarizes the chip performance. At 1.8 V supply and 50 MS/s,the total power consumption is 2.26 mW. The analog,digital and clock circuits consume 0.66,1.14,and 0.46 mW,respectively. The high power of clock block and digital circuit is mainly caused by the synchronous clock generator and the pulse signal generator used in the SAR control logic. The figure-of-merit (FOM) is used to compare the proposed ADC with other works,which is defined as

$$\begin{align} {\rm FOM}=\frac{\rm Power}{2^{{\rm ENOB}}f_{\rm s}}, \end{align}$$

(10)

where $f_{\rm s}$ is the sampling frequency and ENOB is the effective number of bits. The FOM of the proposed ADC is 73.7 fJ/conversion-step. The comparison with other state-of-the-art SAR ADCs is shown in Table2.

5. 5. Conclusions

A 10 bit 50 MS/s SAR ADC fabricated in TSMC 0.18~$\mu$m CMOS process has been proposed. A partial split capacitor switching scheme is adopted to reduce the settling time of DAC leading to improving the conversion speed of the SAR ADC. In addition,a novel logic control technique is proposed,which can pass the comparator output to the DAC network directly and minimize the logic delay. The measurement results indicate that the ADC achieves SFDR of 69.3 dB and SNDR of 57.5 dB with 2.26 mW power consumption. The ADC core area is 0.096 mm$^{2}$.