| Citation: |
Jia Yunpeng, Su Hongyuan, Jin Rui, Hu Dongqing, Wu Yu. Simulation study on single event burnout in linear doping buffer layer engineered power VDMOSFET[J]. Journal of Semiconductors, 2016, 37(2): 024008. doi: 10.1088/1674-4926/37/2/024008
****
J Y peng, S H yuan, J Rui, H D qing, W Yu. Simulation study on single event burnout in linear doping buffer layer engineered power VDMOSFET[J]. J. Semicond., 2016, 37(2): 024008. doi: 10.1088/1674-4926/37/2/024008.
|
Simulation study on single event burnout in linear doping buffer layer engineered power VDMOSFET
DOI: 10.1088/1674-4926/37/2/024008
-
Abstract
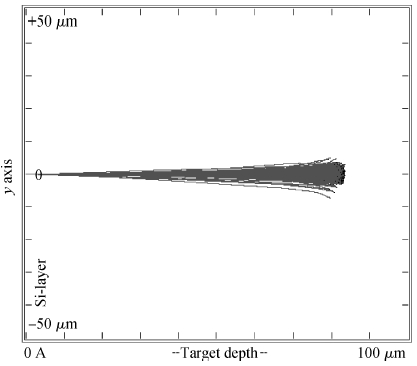
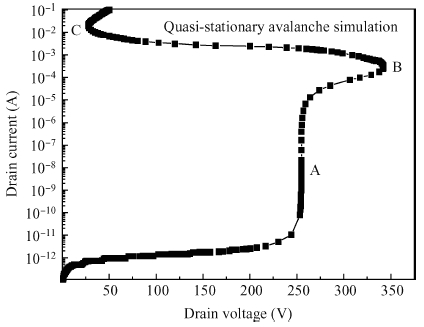
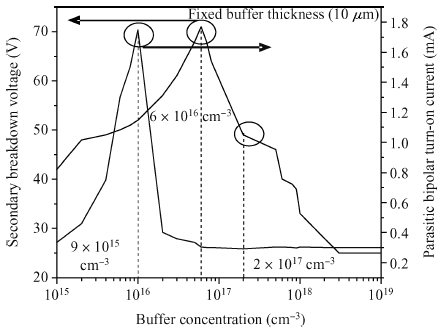
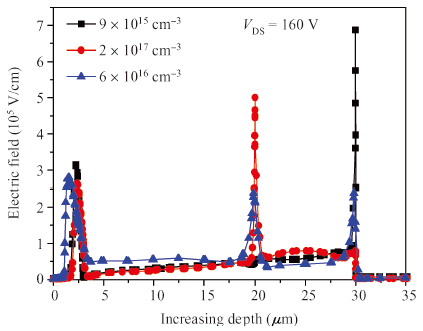
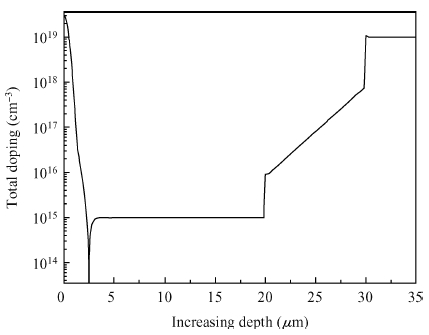
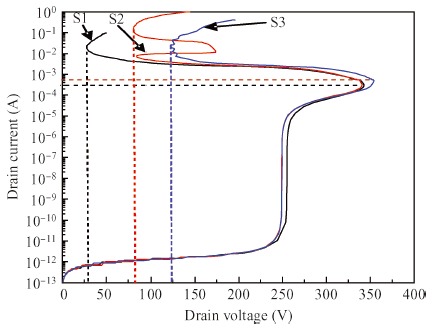
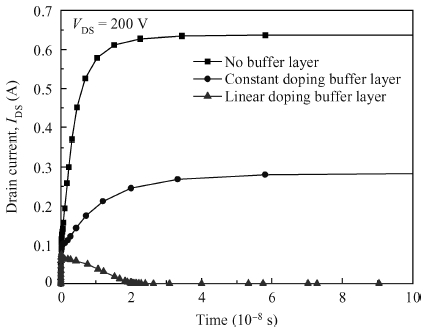
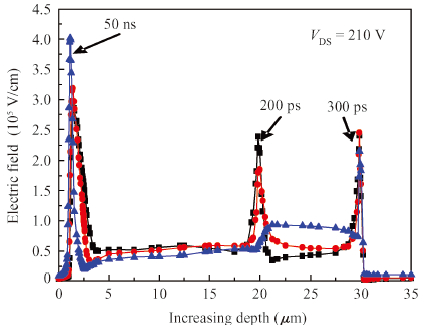
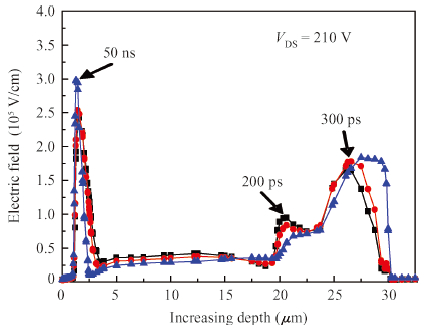
The addition of a buffer layer can improve the device's secondary breakdown voltage, thus, improving the single event burnout (SEB) threshold voltage. In this paper, an N type linear doping buffer layer is proposed. According to quasi-stationary avalanche simulation and heavy ion beam simulation, the results show that an optimized linear doping buffer layer is critical. As SEB is induced by heavy ions impacting, the electric field of an optimized linear doping buffer device is much lower than that with an optimized constant doping buffer layer at a given buffer layer thickness and the same biasing voltages. Secondary breakdown voltage and the parasitic bipolar turn-on current are much higher than those with the optimized constant doping buffer layer. So the linear buffer layer is more advantageous to improving the device's SEB performance. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] -
Proportional views





 DownLoad:
DownLoad: