Fig. 1.
Designed PC corner structures. Block is poly (PC), gray is active (RX), 113 is the minimum space between PC and RX. Both of the structures have 10 devices in parallel
DownLoad:
| Citation: |
Wei Sun, Dake Yang. The corner rounding modeling technique in SPICE simulations for deeply scaled MOSFETs[J]. Journal of Semiconductors, 2013, 34(11): 114008. doi: 10.1088/1674-4926/34/11/114008
****
W Sun, D K Yang. The corner rounding modeling technique in SPICE simulations for deeply scaled MOSFETs[J]. J. Semicond., 2013, 34(11): 114008. doi: 10.1088/1674-4926/34/11/114008.
|
The corner rounding modeling technique in SPICE simulations for deeply scaled MOSFETs
DOI: 10.1088/1674-4926/34/11/114008
More Information
-
Abstract
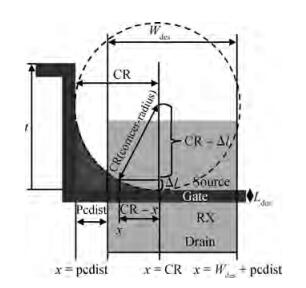
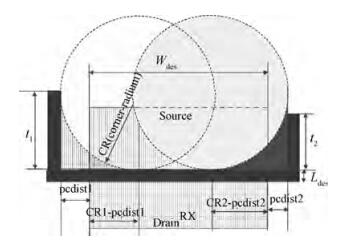
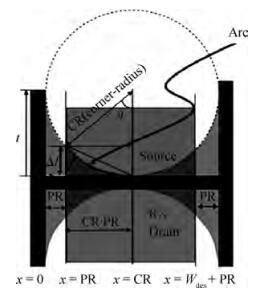
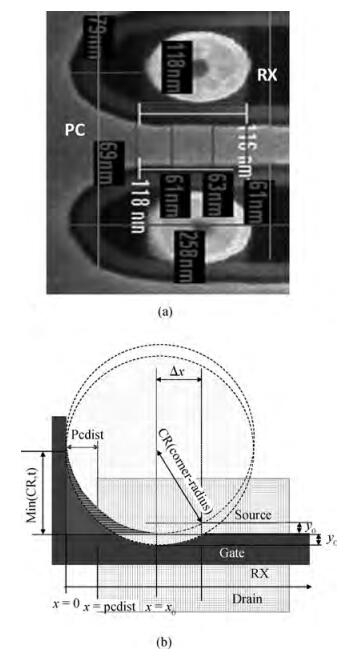
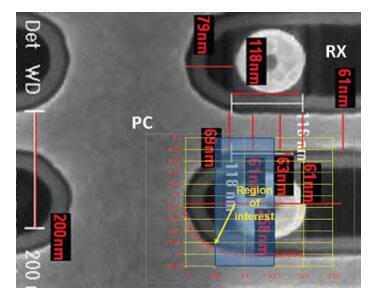
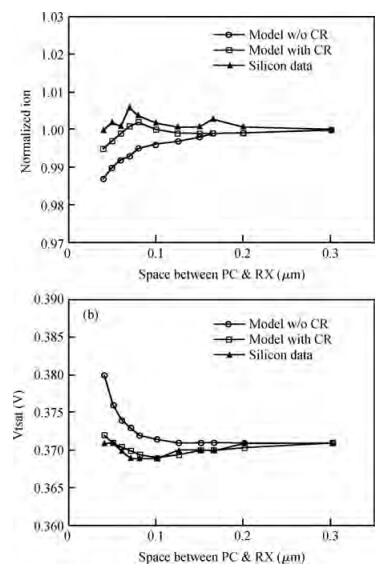
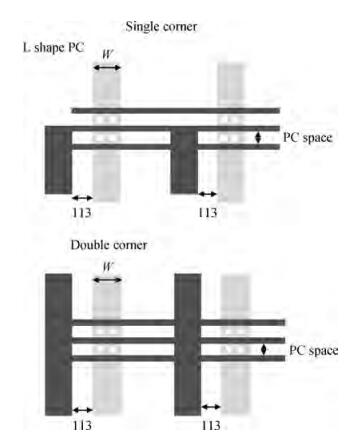
This paper presents a novel poly (PC) and active (RX) corner rounding modeling approach to SPICE simulations. A set of specially designed structures was used for measurement data collection. PC and RX corner rounding equations have been derived based on an assumption that the corner rounding area is a fragment of a circle. The equations were modified to reflect the gouging effect of physical silicon wafers. The modified general equations were implemented in the SPICE model to enable the model to describe the corner rounding effect. The good fittings between the SPICE model simulation results and the silicon data demonstrated in this paper proved that the designed corner rounding model is practical and accurate.-
Keywords:
- SPICE model,
- MOSFETs,
- poly and active,
- corner rounding,
- nanometer technology
-
References
[1] Rozvany G I N, Obieszczanski-Sobieski J S. New optimality criteria methods:forcing uniqueness of the adjoint strains by corner-rounding at constraint intersections. Structural Optimization, 1992, 4:244 doi: 10.1007/BF01742752[2] Sobieszczansld-Sobiesld J. A technique for locating function roots and for satisfying equality constraints in optimization. Structural Optimization, 1992, 4:241 doi: 10.1007/BF01742751[3] Arora S, Karger D, Karpinski M. Polynomial-time approximation schemes dense instances of NP-hard optimization problems. J Computer Syst Sci, 1999, 58(1):193 doi: 10.1006/jcss.1998.1605[4] Rolim J D P, Trevisan L. A case study of de-randomization methods for combinatorial approximation problems. Journal of Combinatorial Optimization, 1998, 2(3):219 doi: 10.1023/A:1009793909670[5] Afrati F, Bampis E, Chekuri C. Approximation schemes for minimizing average weighted completion time with release dates. Proceedings of the 40th IEEE FOCS, 1999:32[6] Xue J, Deng Z, Koo K, et al. Integrated mask and optics simulations for mask corner rounding effect in OPC modeling. Proc SPIE Photomask Technology, 2010, 7823:41[7] Lucas K, Postnikov S, Patterson K. Achieving the 90 nm lithography generation with model-based OPC. Future Fab International, 2002:13[8] Lucas K, Word J, Vandenbergh G. Model-based OPC for 1st generation 193 nm lithography. Proc SPIE, 2001:4346[9] Van Driessche V, Lucas K, van Roey F. 100 nm generation contact patterning by low temperature 193 nm resist reflow process. Proc SPIE, 2002:4690 -
Proportional views
