| Citation: |
Qinghu Zhong, Xuehua Yi, Shouliang Pu, Yuzhen Yan. One-phonon resonant electron Raman scattering in multilayer coaxial cylindrical AlxGa1-xAs/GaAs quantum cables[J]. Journal of Semiconductors, 2013, 34(4): 042001. doi: 10.1088/1674-4926/34/4/042001
****
Q H Zhong, X H Yi, S L Pu, Y Z Yan. One-phonon resonant electron Raman scattering in multilayer coaxial cylindrical AlxGa1-xAs/GaAs quantum cables[J]. J. Semicond., 2013, 34(4): 042001. doi: 10.1088/1674-4926/34/4/042001.
|
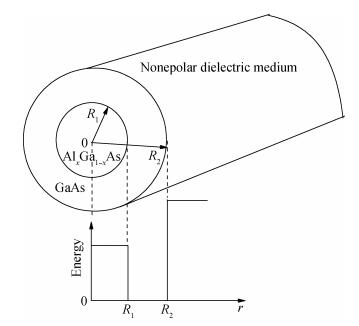
One-phonon resonant electron Raman scattering in multilayer coaxial cylindrical AlxGa1-xAs/GaAs quantum cables
DOI: 10.1088/1674-4926/34/4/042001
More Information
-
Abstract
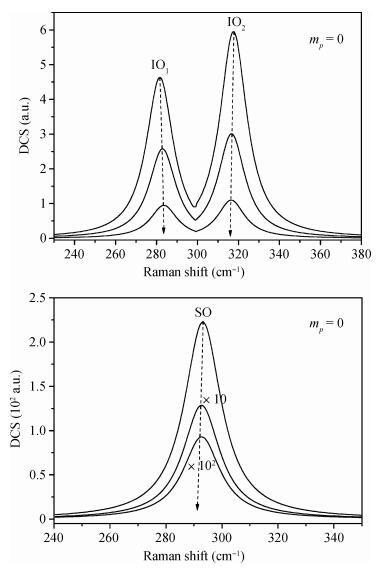
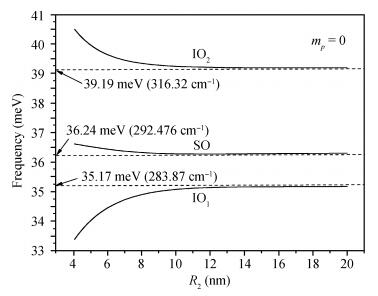
We have presented a theoretical calculation of the differential cross section (DCS) for the electron Raman scattering (ERS) process associated with the interface optical (IO) and surface optical (SO) phonons in multilayer coaxial cylindrical AlxGa1-xAs/GaAs quantum cables (QC). We consider the Fröhlich electron-phonon interaction in the framework of the dielectric continuum approach. The selection rules for the processes are studied. Singularities are found to be sensitively size-dependent and by varying the size of the QC, it is possible to control the frequency shift in the Raman spectra. A discussion of the phonon behavior for the QC with different size is presented. The numerical results are also compared with those of experiments.-
Keywords:
- Raman scattering,
- optical phonon modes,
- quantum cables
-
References
[1] Eychmüller A, Mews A, Weller H. A quantum dot quantum well:CdS/HgS/CdS. Chem Phys Lett, 1993, 208:59 doi: 10.1016/0009-2614(93)80076-2[2] Mews A, Eychmüller A, Giersig M, et al. Preparation, characterization, and photophysics of the quantum dot quantum well system cadmium sulfide/mercury sulfide/cadmium sulfide. J Phys Chem, 1994, 98:934 doi: 10.1021/j100054a032[3] Wendler L. Hartree-Fock approximation for the quasiparticle properties of the coupled electron-phonon system in quantumwell wires in the presence of a magnetic field. Phys Rev B, 1998, 57:9214 doi: 10.1103/PhysRevB.57.9214[4] Wendler L. Magnetopolarons in quasi-one-dimensional quantum-well wires. Physica B, 1999, 270:172 doi: 10.1016/S0921-4526(99)00074-5[5] Chang K, Xia J B. Spatially separated excitons in quantum-dot quantum well structures. Phys Rev B, 1998, 57:9780 doi: 10.1103/PhysRevB.57.9780[6] Checchetto R, Tosello C, Miotello A, et al. Structural evolution of Fe-Al multilayer thin films for different annealing temperatures. J Phys:Condens Matter, 2001, 13:5[7] Assaid E, Feddi E, Khamkhami J E I, et al. Excitons in InP/InAs inhomogeneous quantum dots. J Phys:Condens Matter, 2003, 15:175 doi: 10.1088/0953-8984/15/2/317[8] Suenaga K, Colliex C, Demoncy N, et al. Synthesis of nanoparticles and nanotubes with well-separated layers of boron nitride and carbon. Science, 1997, 278:653 doi: 10.1126/science.278.5338.653[9] Zhang Y, Suenaga K, Colliex C, et al. Coaxial nanocable:silicon carbide and silicon oxide sheathed with boron nitride and carbon. Science, 1998, 281:973 doi: 10.1126/science.281.5379.973[10] Zeng Z Y, Xiang Y, Zhang L D. Single-particle subband structure of quantum cables. Eur J Phys B, 2000, 17:699 doi: 10.1007/s100510070111[11] Zhang L, Xie H J. Frohlich electron interface and surface optical R phonon interaction Hamiltonian in multilayer coaxial cylindrical AlxGa1-xAs/GaAs/GaAs quantum cables. J Phys:Condens Matter, 2003, 15:5881 doi: 10.1088/0953-8984/15/34/318[12] Cardona M, Güntherodt G. Light scattering in solids V. Topics in applied physics, Vol. 66, Springer, Heidelberg, 1989[13] Klein M V. Phonons in semiconductor superlattices. IEEE J Quantum Electron, 1986, QE-22:1760[14] Comas F, Trallero-Giner C, Perez-Alvarez R J. Interband-intraband electronic Raman scattering in semiconductors. J Phys C, 1986, 19:6479 doi: 10.1088/0022-3719/19/32/021[15] Troccoli M, Belyanin A, Capasso F, et al. Raman injection laser. Nature, 2005, 433:845 doi: 10.1038/nature03330[16] Krauss T D, Wise F W. Raman-scattering study of exciton-phonon coupling in PbS nanocrystals. Phys Rev B, 1997, 55:9860 doi: 10.1103/PhysRevB.55.9860[17] Milekhin A G, Tenne D A, Ahn D R T. Quantum dots and nanowires. In: Bandyopadhyay S, Nalwa H S. ed. Am Sci, Stevenson Ranch, Calif, 2003: 375[18] Zhong Q H, Sun Y T. Surface optical phonon-assisted electron Raman scattering in a free-standing quantum wire with ring geometry. Thin Solid Films, 2011, 519:8178 doi: 10.1016/j.tsf.2011.06.045[19] Wang D C, Zhang Y M, Zhang Y M, et al. Raman analysis of epitaxial graphene on 6H-SiC (0001) substrates under low pressure environment. Journal of Semiconductors, 2011, 32:113003 doi: 10.1088/1674-4926/32/11/113003[20] Zhang G J, Xiu B, Chen Y H, et al. Raman scattering of InAs quantum dots with different deposition thicknesses. Chinese Journal of Semiconductors, 2006, 27:1012[21] Tenne D A, Bakarov A K, Toropov A I, et al. Raman study of self-assembled InAs quantum dots embedded in AlAs:influence of growth temperature. Physica E, 2002, 13:199 doi: 10.1016/S1386-9477(01)00519-7[22] Milekhin A G, Toropov A I, Bakarova A K, et al. Resonant Raman scattering in nanostructures with InGaAs/AlAs quantum dots. JETP Lett, 2006, 83:83[23] Krauss T K, Wise F W. Raman-scattering study of excitonphonon coupling in PbS nanocrystals. Phys Rev B, 1997, 55:9860. doi: 10.1103/PhysRevB.55.9860[24] Sood A K, Menéndez J, Cardona M, et al. Interface vibrational modes in GaAs-AlAs superlattices. Phys Rev Lett, 1985, 54:2115 doi: 10.1103/PhysRevLett.54.2115[25] Hayashi S, Kanamori H. Raman scattering from the surface phonon mode in GaP microcrystals. Phys Rev B, 1982, 26:7079 doi: 10.1103/PhysRevB.26.7079[26] Chamberlain M P, Trallero-Giner C, Cardona M. Raman scattering from the surface phonon mode in GaP microcrystals. Phys Rev B, 1995, 51:3[27] Zhong Q H, Liu C H. Studies of electronic Raman scattering in CdS/HgS cylindrical quantum dot quantum well structures. Thin Solid Films, 2008, 516:3405 doi: 10.1016/j.tsf.2007.10.118[28] Liu C H, Ma B K, Chen C Y. Surface optical phonon-assisted electron Raman scattering in a semiconductor quantum disc. Chinese Physics, 2002, 11:7[29] Zhao X F, Liu C H. One phonon resonant Raman scattering in free-standing quantum wires. Physics Letters A, 2007, 364:70 doi: 10.1016/j.physleta.2006.12.070[30] Adachi S. GaAs, AlAs, and AlxGa1-xAs/GaAs:material parameters for use in research and device applications. J Appl Phys, 1985, 58:3[31] Sikorski C H, Merkt U. Spectroscopy of electronic states in InSb quantum dots. Phys Rev Lett, 1989, 62:2164 doi: 10.1103/PhysRevLett.62.2164 -
Proportional views





 DownLoad:
DownLoad: