| Citation: |
Jing Zhou, Lixi Wan, Jun Li, Huijuan Wang, Fengwei Dai, Daniel Guidotti, Liqiang Cao, Daquan Yu. New de-embedding structures for extracting the electrical parameters of a through-silicon-via pair[J]. Journal of Semiconductors, 2013, 34(4): 045004. doi: 10.1088/1674-4926/34/4/045004
****
J Zhou, L X Wan, J Li, H J Wang, F W Dai, D Guidotti, L Q Cao, D Q Yu. New de-embedding structures for extracting the electrical parameters of a through-silicon-via pair[J]. J. Semicond., 2013, 34(4): 045004. doi: 10.1088/1674-4926/34/4/045004.
|
New de-embedding structures for extracting the electrical parameters of a through-silicon-via pair
DOI: 10.1088/1674-4926/34/4/045004
More Information
-
Abstract
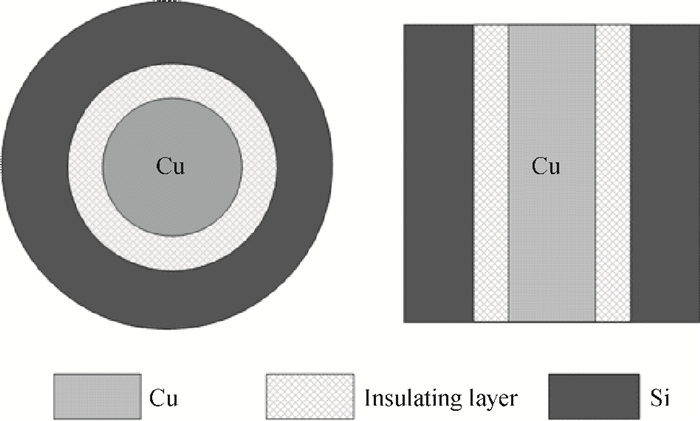
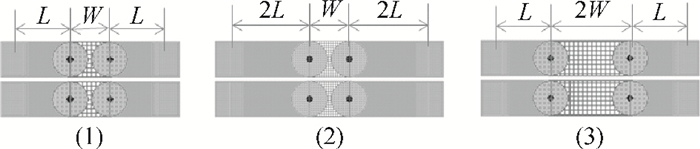
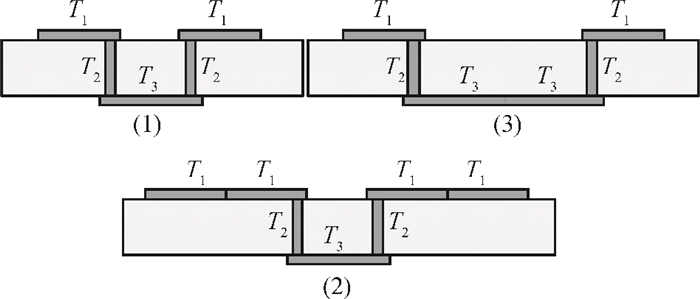
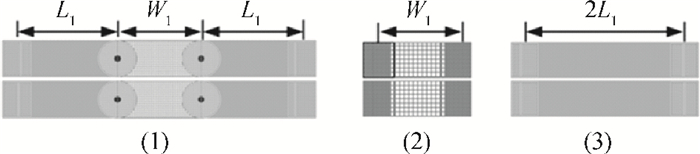
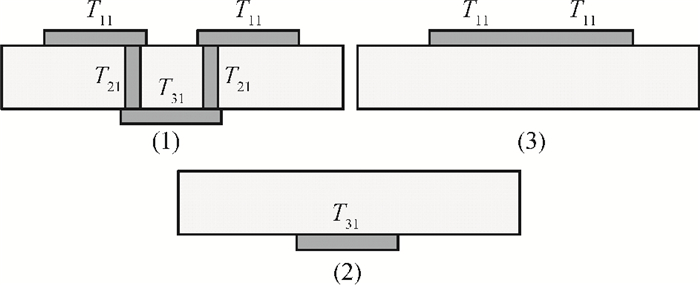
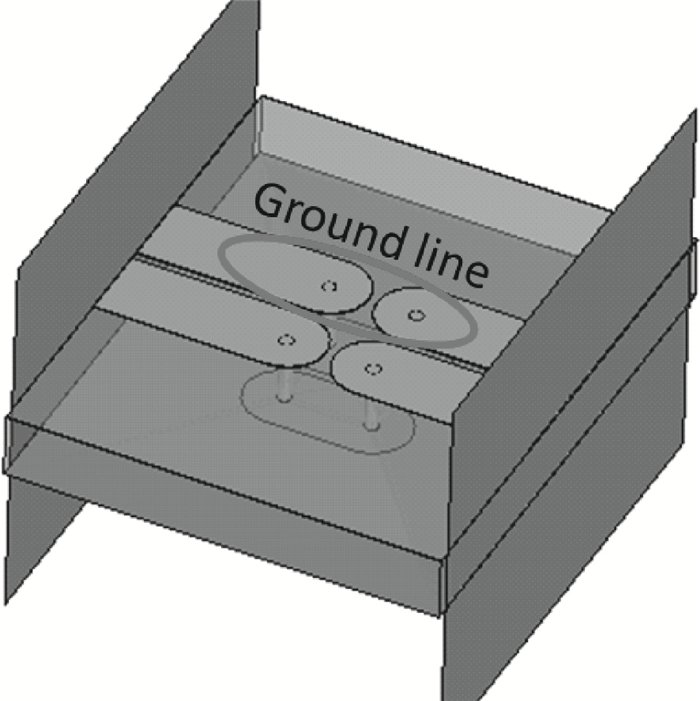
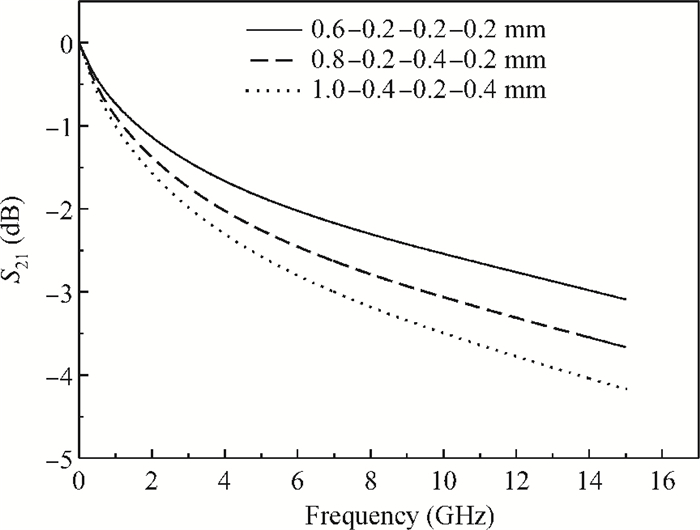
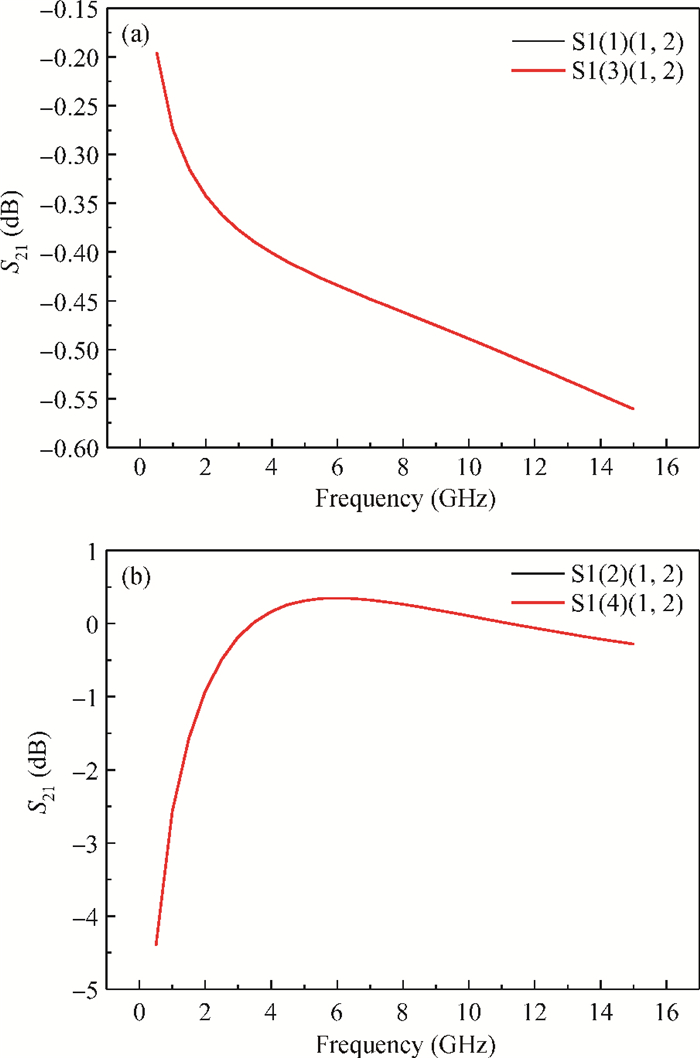
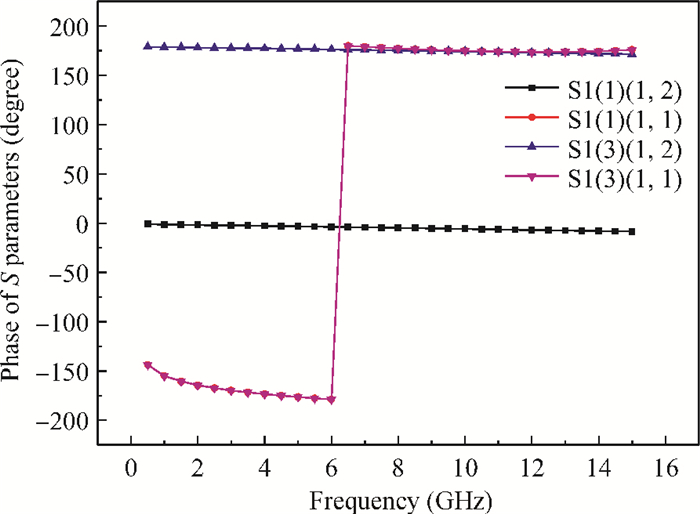
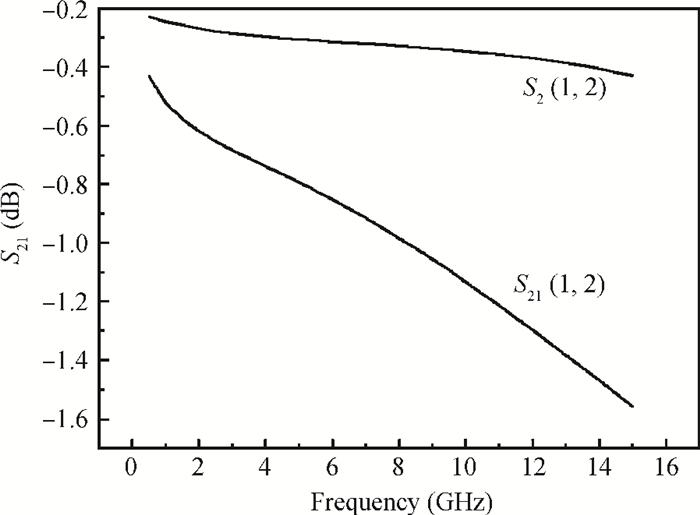
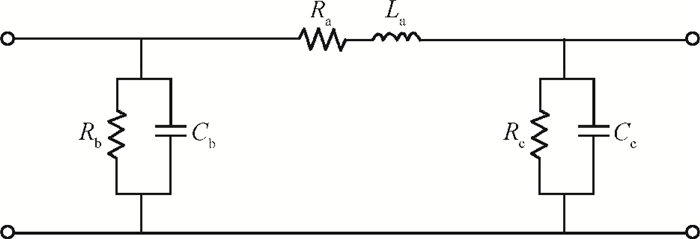
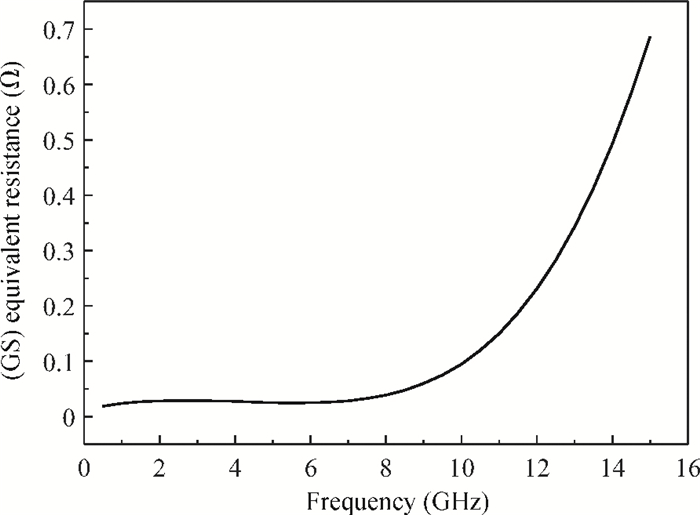
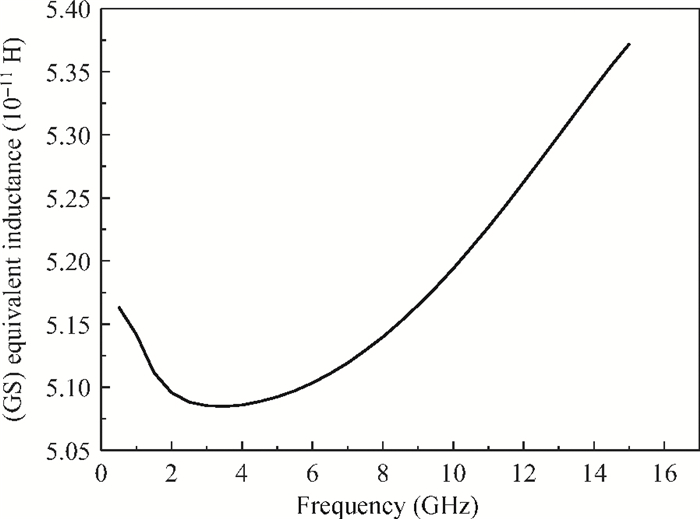
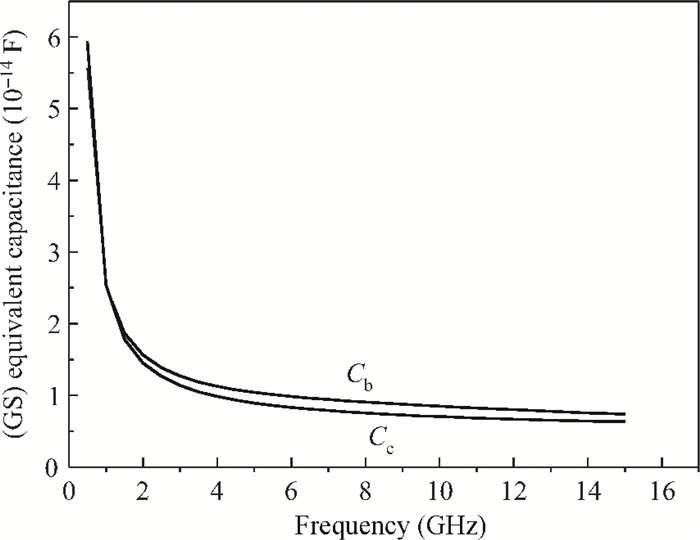
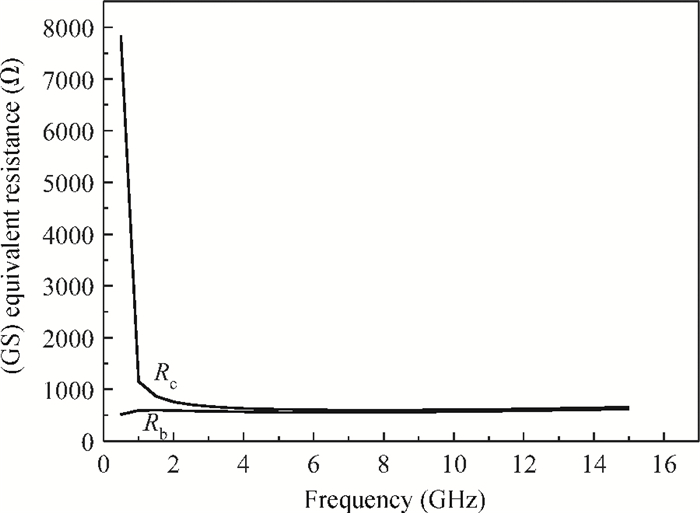
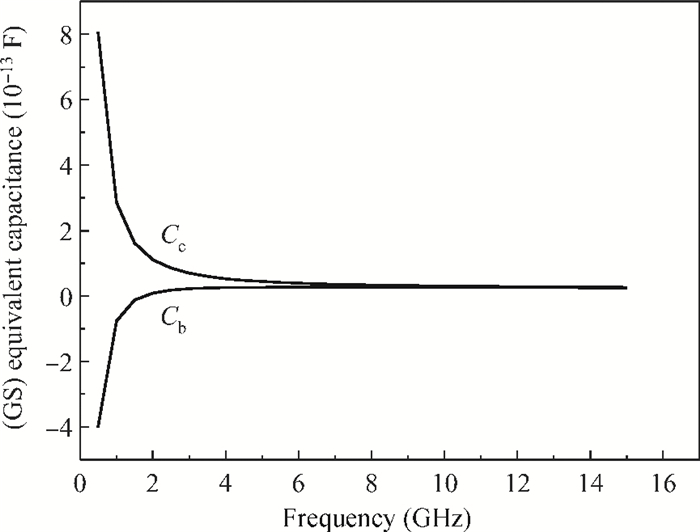
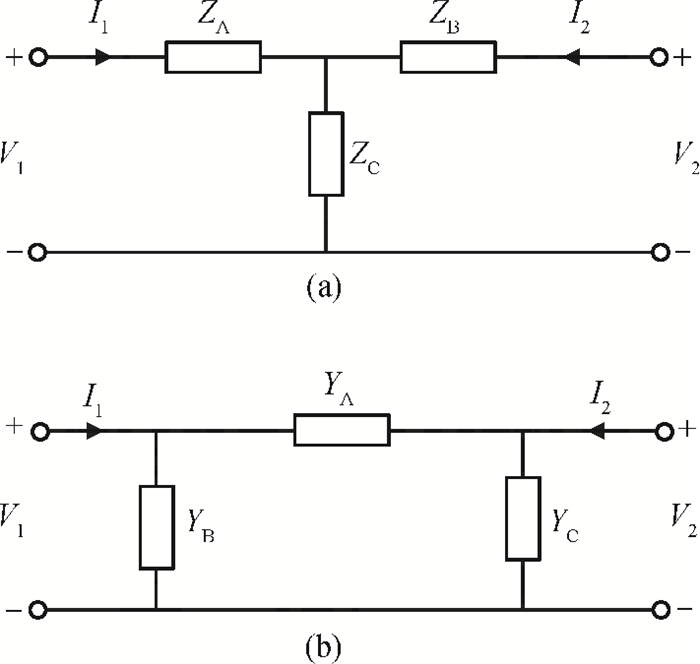
Two innovative de-embedding methods are proposed for extracting an electrical model for a through-silicon-via (TSV) pair consisting of a ground-signal (GS) structure. In addition, based on microwave network theory, a new solution scheme is developed for dealing with multiple solutions of the transfer matrix during the process of de-embedding. A unique solution is determined based on the amplitude and the phase characteristic of S parameters. In the first de-embedding method, a typical "π" type model of the TSV pair is developed, which illustrates the need to allow for frequency dependence in the equivalent TSV pair Spice model. This de-embedding method is shown to be effective for extracting the electrical properties of the TSVs. The feasibility of a second de-embedding method is also investigated. -
References
[1] Zhou J, Wan L, Dai F, et al. Accurate electrical simulation and design optimization for silicon interposer considering the MOS effect and eddy currents in the silicon substrate. Proc 63th Electronic Components and Technology Conference, 2012:658 http://ieeexplore.ieee.org/document/6248902/?arnumber=6248902&punumber%3D6241679[2] Kamgaing T, Elsherbini A, Rao V. Design acceleration of embedding RF inductors on a multilayer flip chip package substrate. Proc 62th Electronic Components and Technology Conference, 2010:133 http://ieeexplore.ieee.org/document/5898503/authors[3] Cadix L, Bermond C, Fuchs C, et al. RF characterization and modelling of high density through silicon vias for 3D chip stacking. Microelectron Eng, 2010, 87:491 doi: 10.1016/j.mee.2009.08.026[4] Kim J, Pak J S, Cho J, et al. High-frequency scalable electrical model and analysis of a through silicon via (TSV). IEEE Trans Comp Packag Manuf Technol, 2011, 1(2):181 doi: 10.1109/TCPMT.2010.2101890[5] Katti G, Stucchi M, Meyer K D, et al. Electrical modeling and characterization of through silicon via for three-dimensional ICs. IEEE Trans Electron Devices, 2010, 57(1):256 doi: 10.1109/TED.2009.2034508[6] Liu E X, Li E P, Ewe W B, et al. Compact wideband equivalent-circuit model for electrical modeling of through-silicon via. IEEE Trans Microw Theory Tech, 2011, 59(6):1454 doi: 10.1109/TMTT.2011.2116039[7] Xu C, Li H, Suaya R, et al. Compact AC modeling and performance analysis of through-silicon vias in 3-D ICs. IEEE Trans Electron Devices, 2010, 59(6):3405 https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005613162[8] Vandamme E P, Schreurs D M M P, van Dinther C. Improved three-step de-embedding method to accurately account for the influence of pad parasitics in silicon on-wafer RF test-structures. IEEE Tran Electron Devices, 2001, 48(4):737 doi: 10.1109/16.915712[9] Tiemeijer L F, Havens R J, Jansman A B M, et al. Comparison of the "pad-open-short" and "open-short-load" deembedding techniques for accurate on-wafer RF characterization of high-quality passives. IEEE Trans Microw Theory Tech, 2005, 53(2):723 doi: 10.1109/TMTT.2004.840621[10] Fourneaud L, Lacrevaz T, Charbonnier J. Innovative HF extraction procedure of the characteristic impedance for embedding planar transmission line on high conductive Si substrate. Proc Asia-Pacific Microwave Conference, 2010:606 http://ieeexplore.ieee.org/document/5728364/[11] Fourneaud L, Lacrevaz T, Charbonnier J, et al. Extraction of equivalent high frequency models for TSV and RDL interconnects embedding in stacks of the 3D integration technology. 15th IEEE Workshop on Digital Object Identifier Signal Propagation on Interconnects (SPI), 2011:61 http://ieeexplore.ieee.org/document/5898841/authors[12] Mong K Y, Kee C E, Guan L T, et al. High frequency characterization of through silicon via structure. Proc 11th Electronics Packaging Technology Conference, 2009:536 https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005416491[13] Sullvan D. The square root of 2×2 matrices. Bulletin des Sciences Mathe'matiques, 1996, (4):42 http://www.maa.org/sites/default/files/Square_Roots-Sullivan13884.pdf -
Proportional views





 DownLoad:
DownLoad: