Fig. 1.
Relational curves of the ground-state energy $E_0$ with the aspect ratio $e'$ of the QR at different electron-phonon coupling
DownLoad:
| Citation: |
Wei Xin, Yuwei Zhao, Chao Han, Eerdunchaolu. Magnetic field and temperature dependence of the properties of the ground state of the strong-coupling bound magnetopolaron in quantum rods with hydrogenic impurity[J]. Journal of Semiconductors, 2013, 34(5): 052001. doi: 10.1088/1674-4926/34/5/052001
****
W Xin, Y W Zhao, C Han, E E D C lu. Magnetic field and temperature dependence of the properties of the ground state of the strong-coupling bound magnetopolaron in quantum rods with hydrogenic impurity[J]. J. Semicond., 2013, 34(5): 052001. doi: 10.1088/1674-4926/34/5/052001.
|
Magnetic field and temperature dependence of the properties of the ground state of the strong-coupling bound magnetopolaron in quantum rods with hydrogenic impurity
DOI: 10.1088/1674-4926/34/5/052001
More Information
-
Abstract
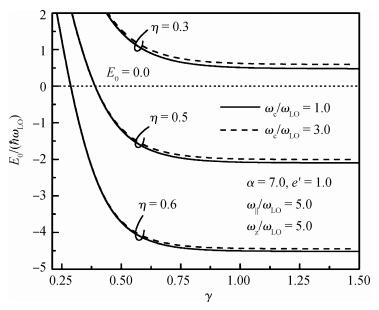
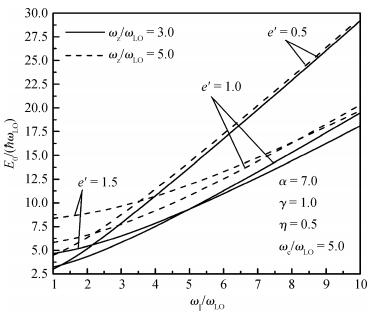
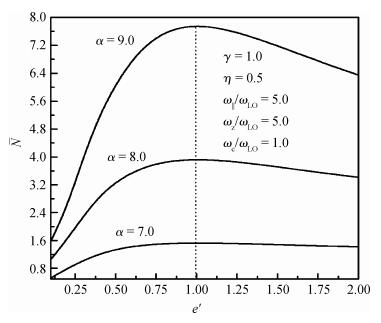
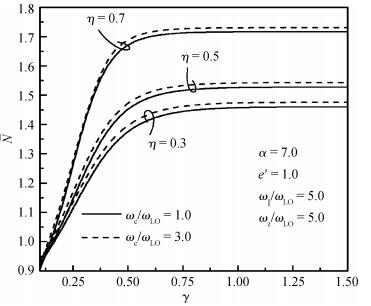
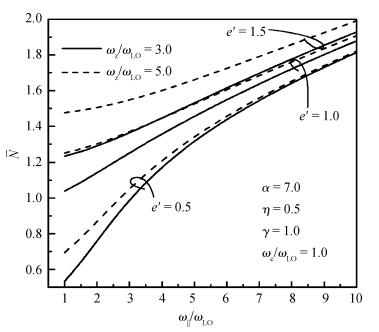
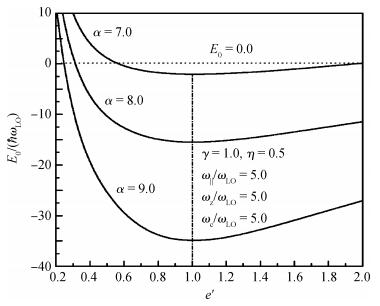
Magnetic field and temperature dependence of the properties of the ground state of the strong-coupling bound magnetopolaron in quantum rods (QRs) with hydrogenic impurity is studied by means of the Huybrechts-Lee-Low-Pines transformation method and the quantum statistical theory. The expressions for the ground-state energy and the mean number of phonons of the magnetopolaron are derived. Results of the numerical calculations show that the bound state of the magnetopolaron cannot be formed when the value of the aspect ratio of the QR, the dielectric constant ratio, the electron-phonon coupling strength or the temperature parameter is small. The larger the deviation of the value of aspect ratio e' from 1 is, the more it is unfavorable to the stability of the ground state of the magnetopolaron. When the magnetopolaron is in the bound state, the absolute value of its ground-state energy and its mean number of phonons increase with an increase of the dielectric constant ratio and confinement strength of QRs, but decrease with an increase in the cyclotron frequency of the external magnetic field and the temperature. The absolute value of the ground-state energy and the mean number of phonons of the magnetopolaron decrease with decreasing e' when e' < 1, but decrease with increasing e' when e' > 1. They get the maximum value at e'=1. -
References
[1] Sun B Q, Jiang D S. Photon localization and lasing in disordered GaNAs optical superlattices. Phys Rev B, 2006, 73:195112 doi: 10.1103/PhysRevB.73.195112[2] Sun B Q, Jiang D S, Sun Z, et al. Photoinduced spin alignment of the magnetic ions in (Ga, Mn)As. J Appl Phys, 2006, 100:83104 doi: 10.1063/1.2358407[3] Li S S, Xia J B. Linear Rashba model of a hydrogenic donor impurity in GaAs/GaAlAs quantum wells. Nanoscale Res Lett, 2009, 4:178 doi: 10.1007/s11671-008-9222-5[4] Yang F, Zheng R S. Properties of optical phonons in Zn1-x-yMgyBexSe quaternary mixed crystal. Solid State Commun, 2007, 141:555 doi: 10.1016/j.ssc.2006.12.022[5] Gong J, Liang X X, Ban S L. Confined LO-phonon assisted tunneling in a parabolic quantum well with double barriers. J Appl Phys, 2006, 100:023707 doi: 10.1063/1.2218761[6] Eerdunchaolu, Xiao J L. Effects of lattice vibration on the properties of the strong-coupling polaron in a quantum well. J Phys Soc Jpn, 2007, 76:044702 doi: 10.1143/JPSJ.76.044702[7] Reed M A, Bate R T, Bradshaw K, et al. Spatial quantization in GaAs-AlGaAs multiple quantum dots. J Vac Sci Technol B, 1986, 4:358[8] Klein M C, Hache F, Ricard E, et al. Size dependence of electron-phonon coupling in semiconductor nanospheres:the case of CdSe. Phys Rew B, 1990, 42:11123 doi: 10.1103/PhysRevB.42.11123[9] Charrour R, Bouhassoune M, Bria D, et al. Polaron effect on the binding energy of shallow donor in cylindrical quantum dot. Acta Phys Pol A, 1999, 96:759 doi: 10.12693/APhysPolA.96.759[10] Melnikov D V, Fowler W B. Electron-phonon interaction in a spherical quantum dot with finite potential barriers:the Fröhlich Hamiltonian. Phys Rew B, 2001, 64:245320 doi: 10.1103/PhysRevB.64.245320[11] Katz D, Wizansky T, Millo O, et al. Size-dependent tunneling and optical spectroscopy of CdSe quantum rods. Phys Rev Lett, 2002, 89:086801 doi: 10.1103/PhysRevLett.89.086801[12] Hu J T, Li L S, Yang W D, et al. Linearly polarized emission from colloidal semiconductor quantum rods. Science, 2001, 292:2060 doi: 10.1126/science.1060810[13] Bruchez M, Moronne M, Gin P, et al. Semiconductor nanocrystals as fluorescent biological labels. Science, 1998, 281:2013 doi: 10.1126/science.281.5385.2013[14] Klimov V I, Mikhailovsky A A, Xu S, et al. Optical gain and stimulated emission in nanocrystal quantum dots. Science, 2000, 290:314 doi: 10.1126/science.290.5490.314[15] Hu J T, Wang L W, Li L S, et al. Semiempirical pseudopotential calculation of electronic states of CdSe quantum rods. J Phys Chem B, 2002, 106(10):2447 doi: 10.1021/jp013204q[16] Li X Z, Xia J B. Electronic structure and optical properties of quantum rods with wurtzite structure. Phys Rev B, 2002, 66:115316 doi: 10.1103/PhysRevB.66.115316[17] Li X Z, Xia J B. Effects of electric field on the electronic structure and optical properties of quantum rods with wurtzite structure. Phys Rev B, 2003, 68:165316 doi: 10.1103/PhysRevB.68.165316[18] Zhang X W, Xia J B. Linear-polarization optical property of CdSe quantum rods. Chinese Journal of Semiconductors, 2006, 27:2094[19] Zhang X W, Zhu Y H, Xiao J B. Optical properties and g factors of GaAs quantum rods. Physica E, 2006, 33:376 doi: 10.1016/j.physe.2006.04.009[20] Climente J I, Royo M, Movilla J L, et al. Strong configuration mixing due to dielectric confinement in semiconductor nanorods. Phys Rev B, 2009, 79:161301 doi: 10.1103/PhysRevB.79.161301[21] Fai L C, Teboul V, Monteil A, et al. Polaron in a quasi 1D cylindrical quantum wire. Condensed Matter Physics, 2005, 8:639 doi: 10.5488/CMP.8.3.639[22] Comas F, Studart N, Marques G E. Optical phonons in semiconductor quantum rods. Solid State Commun, 2004, 130:477 doi: 10.1016/j.ssc.2004.02.037[23] Wang C T, Xiao J L, Zhao C L. Ground-state energy of weak-coupling polarons in quantum rods. Journal of Semiconductors, 2009, 30:072002 doi: 10.1088/1674-4926/30/7/072002[24] Wang G W, Xiao J L. Frequency of the transition spectra line of an electron in quantum rods. Journal of Semiconductors, 2010, 31:092002 doi: 10.1088/1674-4926/31/9/092002[25] Huybrechts W J. Note on the ground-state energy of the Feynman polaron model. J Phys C:Solid State Phys, 1976, 9:L211[26] Lee T D, Low F M, Pines D. The motion of slow electrons in a polar crystal. Phys Rev, 1953, 90:297 doi: 10.1103/PhysRev.90.297[27] Brummell M A, Nicholas R J, Hopkins M A, et al. Modification of the electron-phonon interactions in GaAs-GaAlAs heterojunctions. Phys Rev Lett, 1987, 58:77 doi: 10.1103/PhysRevLett.58.77 -
Proportional views
